
Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013
.pdf
Министерство образования и науки Российской федерации
Санкт-Петербургский государственный архитектурно-строительный университет
В. В. КАРПОВ, А. Н. ПАНИН
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РАСЧЕТ ЭЛЕМЕНТОВ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Учебное пособие
Санкт-Петербург
2013
1

Математическое моделирование и расчет элементов строительных конструкций
УДК 519.6, 624.046, 539.3
Рецензенты: д-р техн. наук, профессор В. В. Лалин (СПбПУ); канд. физ.-мат. наук, доцент Т. В. Рябикова (ПГУПС)
Карпов, В. В.
Математическоемоделирование и расчетэлементовстроительных конструкций: учеб. пособие / В. В. Карпов, А. Н. Панин;
СПбГАСУ. – СПб., 2013 – 176 с.
ISBN 978-5-9227-0436-6
Приводятсясведенияобосновныхметодахиприемахпостроенияматематических моделей объектов и примеры построения математических моделейнаосновеэтихпринципов.Приводятсяматематическиемодели деформирования балок, плит, оболочек при учете различных свойств материала, алгоритмы исследования их напряженно-деформированного состояния. Рассмотрены примеры расчета элементовстроительных конструкций в линейноупругой, нелинейно-упругой постановках и при учете ползучести материала.
Предназначено для магистрантов направления «Строительство».
Ил. 65. Табл. 13. Библиогр. 29 назв.
РекомендованоРедакционно-издательскимсоветомСПбГАСУвкачестве учебного пособия.
ISBN 978-5-9227-0436-6
©В. В. Карпов, А. Н. Панин, 2013
©Санкт-Петербургский государственный
архитектурно-строительный университет, 2013
ВВЕДЕНИЕ
Всередине прошлого столетия с появлением ЭВМ был разработан новый способ теоретического исследования сложных процессов, допускающих математическое описание, – вычислительный эксперимент,т.е.исследованиеестественнонаучныхпроблемсредствами вычислительной математики.
Суть вычислительногоэкспериментасостоитвтом,что составляется математическая модель изучаемого процесса или явления, которая представляет собой некоторые математические уравнения (алгебраические,дифференциальные,интегральныеидругие),затем разрабатывается вычислительный алгоритм для решения этих уравнений, составляется программа для ЭВМ и проводится расчет конкретныхвариантовсостоянияобъектаприизменениивходящихвуравнения параметров.
Таким образом, основой изучения различных объектов является построение математической модели их функционирования.
Впособии излагаются основные методы и приемы построения математическихмоделейразличныхобъектов иявленийиприводятся конкретные примеры формирования математических моделей на основе фундаментальных законов природы, вариационных принципов, удобных для вывода уравнений равновесия (движения) элементовстроительныхконструкций, идругихподходов.Приводятсяпримеры построения математических моделей при проведении натурного эксперимента и в задачах оптимизации. Для магистрантов направления «Строительство»важным является не только разработка математических моделей деформирования элементов строительных конструкций, но и построение методики исследования напря- женно-деформированного состояния таких конструкций, как балка (стержень), плита (пластина) и оболочка.
Также в пособии изложены методика расчета и примеры расчета элементов строительных конструкций. Отдельная глава пособия посвящена исследованию пологих железобетонных ребристых оболочек с учетомтаких факторов, как физическаянелинейность и пол-
2 |
3 |

Математическое моделирование и расчет элементов строительных конструкций
зучестьматериала, таккактакие конструкции зачастуюиспользуются для покрытия большепролетных строительных сооружений.
Главы 1–3 написаны В. В. Карповым, глава 4 – А. Н. Паниным. Авторыблагодарнырецензентам:заведующемукафедройстроительной механики и теории упругости СПбГПУ доктору технических наук, профессору В. В. Лалину и кандидату физико-математи- ческих наук, доцентуТ.В. Рябиковой(ПГУПС). Авторыпризнатель-
ны Д. В. Холод за помощь при подготовке рукописи к изданию.
Глава 1. ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
1.1. Физическое и математическое моделирование
Под моделированием понимается исследование различных процессов на моделях. Различают физическое и математическое моделирование. В случае физического моделирования модель воспроизводит изучаемый процесс с сохранением его физической природы (продувка моделей самолетов в аэродинамических трубах, изучениесвойствгидротехническихсооруженийприпомощимакетов русловыхпотоковит.д.).Прифизическоммоделированииотношения величин в натуре к соответствующим величинам на модели должны быть постоянными (например, отношения линейных размеров). Эти отношения называются коэффициентами подобия. Физическое моделирование имеет ограниченную сферу применения.
Более широкими возможностями обладает математическое моделирование как метод исследования различных процессов путем описания их функционирования с помощью математических соотношений [13, 24]. Таким образом, при изучении процессов методом математического моделирования в первую очередь необходимопостроитьматематическоеописаниеизучаемогопроцесса. Математическая модель реального процесса есть некоторый математический объект, поставленный в соответствие данному физическому процессу, т. е. математическое описание физического процесса с помощью алгебраических, дифференциальных, интегральныхи других уравнений. Эти уравнения обычно выражают законы сохранения основных физических величин (энергии, количества движения, массы и др.) и связывают характеристики процесса с параметрами соответствующей системы, исходной информацией и начальными условиями.
После составления математической модели объекта проводится исследование этой модели, т. е. проводится вычислительный эксперимент.
4 |
5 |

Математическое моделирование и расчет элементов строительных конструкций
Следует подчеркнуть, что одному и тому же объекту можно поставитьвсоответствиенеоднуматематическуюмодель,анесколько. Исходя из поставленных задач исследования объекта, выбираетсянаиболееоптимальнаяматематическаямодельвсмыслесложности модели и точности воспроизведения поведения объекта.
Сама постановка вопроса о математическом моделировании какого-либо объекта порождает четкий план действий. Его можно условно разбить на три этапа: модель – алгоритм – программа (для ЭВМ) (рис. 1.1).
Модель
Объект
Программа Алгоритм
Рис. 1.1. Основные этапы исследования объекта
1.2. Основные этапы процесса построения математической модели объекта
Выделимосновные этапывпроцессе построенияматематической модели объекта.
1.Конструирование модели начинается со словесно-смыслово- го описания объекта или явления. Помимо сведений общего характера о природе объекта и целях его исследования эта стадия может содержать также некоторые предположения, упрощающие модель
ивыделяющиеосновныехарактеристикиповеденияобъекта.Наэтом этапе как бы формируется физическая модель объекта.
2.Следующий этап – завершение идеализации объекта. Отбрасываютсявсефакторыиэффекты,которыепредставляютсянесамыми существеннымидля его поведения. Повозможности идеализирующие предположения записываются в математической форме, с тем чтобы их справедливость поддавалась количественному контролю.
3.После выполнения первых двух этапов можно переходить
квыбору или формулировке закона (фундаментального закона при-
Глава 1. Основы математического моделирования
роды, вариационного принципа, аналогии и т. п.), которому подчиняется объект, и его записи в математической форме. При необходимости используются дополнительные сведения об объекте, также записываемые математически. Следует иметь в виду, что даже для простых объектов выбор соответствующего закона отнюдь не тривиальная задача.
4.Завершают формулировку модели такие факторы, как задание сведений о начальном состоянии объекта или иные его характеристики (начальные и краевые условия для полученных уравнений, значения входящих в уравнение констант и известных функций), без знания которых невозможно определить поведение объекта. И наконец, формируется цель исследования модели (какие величины, характеризующие поведение объекта, необходимо найти на модели).
5.Построенная модель изучается всеми доступными исследователю методами, в том числе со взаимной проверкой различных подходов.Анализируетсякорректностьполученныхматематических соотношений. Затем подбирается метод решения полученных уравнений, составляющих модель, и производится алгоритмизация задачи. Если решение не удается найти аналитически, то по разработанному алгоритму составляется программа расчета на ЭВМ и проводится сам расчет.
6.В результате исследования модели не только достигается поставленная цель, но и должна быть установлена всеми возможными способами (сравнением с экспериментом, сопоставлением с другими подходами) ее адекватность – соответствие объекту и сформулированным предположениям. Если модель не отвечает поставленным требованиям, то необходимо модель видоизменить и улучшить.
1.3.Основные методы и приемы построения математических
моделей
Чтобы реальный физический процесс описать математическими зависимостями, используются разные приемы и методы, исходя из природы процесса исследования [13, 24]. Пожалуй, основной метод построения математических моделей основан на применении фундаментальных законов природы, таких как сохранение энергии, сохранение массы вещества, сохранение импульса, сохранение чис-
6 |
7 |

Математическое моделирование и расчет элементов строительных конструкций
ла частиц и др. Может применяться для построения математических моделей метод, основанный на вариационных принципах, а также принцип аналогий, иерархический подход, подход, основанный на приравнивании к нулю проекций всех силовых факторов (внутренних и внешних) по соответствующим направлениям осей координат.
Изучение некоторых процессов возможно только опытным пу- тем–спомощьюпроведенияэксперимента.Приэтомдляполучения математической модели изучаемого экспериментально процесса используются для обработки полученных экспериментально данных (случайных величин) и обоснования достоверности найденных величин (средних значений, дисперсии, законов распределения) мето- дыматематическойстатистики,иметоднаименьшихквадратов–для полученияаналитическойзависимостивыходногопараметраотвходных параметров (факторов).
В некоторых случаях (например, при рассмотрении задач оптимизации) достаточно формализовать словесное описание процесса (записать с помощью математических символов связь известных и искомых величин, введя буквенные обозначения) и тем самым получить математическую модель изучаемого процесса.
1.4. Получение математических моделей на основе фундаментальных законов природы
1.4.1. Модели, полученные на основе закона сохранения энергии
Чтобы использовать какие-то законы природы для вывода математическоймоделиобъектаилипроцесса,нужнохорошопредставлять эти законы.
Кроме того, необходимы знания из той области, для объектов которой строится математическая модель. Если, например, хотим построить описание процесса теплопередачи, то нужно знать, каковы характеристики этого процесса.
Тепловаяэнергия,илитепло– этоэнергияхаотическогодвижения атомов или молекул вещества. Обмен теплом между различными участками материала называется теплопередачей, а сами материалы, обладающие хорошо выраженным свойством теплопередачи, –
Глава 1. Основы математического моделирования
теплопроводными. К ним относятся, например, металлы, в которых тепловая энергия переносится в основном свободными электронами, некоторые газы и т. п. Процессы передачи тепла рассматриваются вусловиях так называемого локальноготермодинамического равновесия. Понятие локального термодинамического равновесия для
газов вводится при λ << L, т. е. когда длина свободного пробега частиц вещества много меньше характерных размероврассматриваемого объекта (сплошная среда). Локальное термодинамическое равновесие предусматривает также, что процессы изучаются при временах, бóльших, чем τ (время между столкновениями частиц), и на размерах, бóльших,чем λ.Тогдавобластяхвещества,размерыкото-
рых превосходят величину λ (но много меньше величины L ), уста- навливается равновесие и для них можно ввести средние величины плотности, скорости теплового движения частиц и т. д. Эти локальные величины (разные в разных точках среды) при сформулированных предположениях находятся из равновесного максвелловского
распределения частиц. К ним относится и температура T , определяющая среднюю кинетическую энергию частиц:
mv2 2 = 32 kT ,
где m – масса частицы; v – средняя скорость хаотического движе-
ния; k – постоянная Больцмана.
Связанная с хаотическим движением частиц энергия вещества (внутренняя энергия) определяется через температуру с помощью
величины удельной теплоемкости с(ρ, T ), а именно
с(ρ,T ) = ∂ε(∂ρT,T ), с(ρ,T ) > 0,
где ρ = m n –плотностьвещества (n –числочастицвединице объема); ε(ρ,T ) – внутренняя энергия единицы массы.
Другими словами, теплоемкость – это энергия, которую надо сообщить единице массы вещества, чтобы увеличить его температуру на один градус.
Наиболее простое выражение для теплоемкости получается в случае идеального газа (газа, частицы которого взаимодействуют лишьпринепосредственномстолкновениии, подобно биллиардным
8 |
9 |
Математическое моделирование и расчет элементов строительных конструкций
шарам, без потерисуммарной кинетической энергии). Теплоемкость
3k
идеального газа не зависит от величин ρ, T и равна 2m , так как
ε= 23mk T.
Вобщем случае связь между внутренней энергией и температуройболее сложная.Например,помимо кинетическойэнергиидвижущихся частиц, внутренняя энергия содержит составляющую, связанную с потенциальной энергией их взаимодействия, зависящей от среднего расстояния r между ними. Поэтому в теории теплопереда-
чи величины и c являются функциями от ρ и T . Их конкретный вид определяется свойствами рассматриваемой среды.
Для получения математической модели теплопередачи необходимо, помимо описанных выше понятий, ввести важное понятие потока тепла. Потоком тепла (или тепловой энергии) в данной точке называетсяколичествотепла,переносимое вединицувременичерез единичную поверхность, помещенную в данную точку вещества. Очевидно, что поток тепла – векторная величина. Компонентами
потока W по соответствующим осям будут Wx , Wy , Wz . Не вдаваясь в подробности, запишем выражение этих компонент:
Wx = −χ∂∂Tx , Wy = −χ∂∂Ty , Wz = −χ∂∂Tz ,
где χ = |
ρcλv |
≥ 0 и называется коэффициентом теплопроводности. |
|
|
3 |
|
|
Для потока W , в соответствии с законом Фурье, имеем |
|
||
|
|
W = −χgradT . |
(1.1) |
Итак, закон Фурье гласит: поток тепла пропорционален градиенту температуры.
Применим закон сохранения энергии для математического описания процесса теплопередачи. Будем считать, что внутренняя энергия вещества изменяется лишь благодаря механизму теплопроводности, т. е. другие виды энергии полагаемнесущественными (например, пренебрегаем изменением внутренней энергии за счет химических реакций или за счет работы сил давления, сжимающих некоторый объем газа, и т. д.).
Глава 1. Основы математического моделирования |
|||
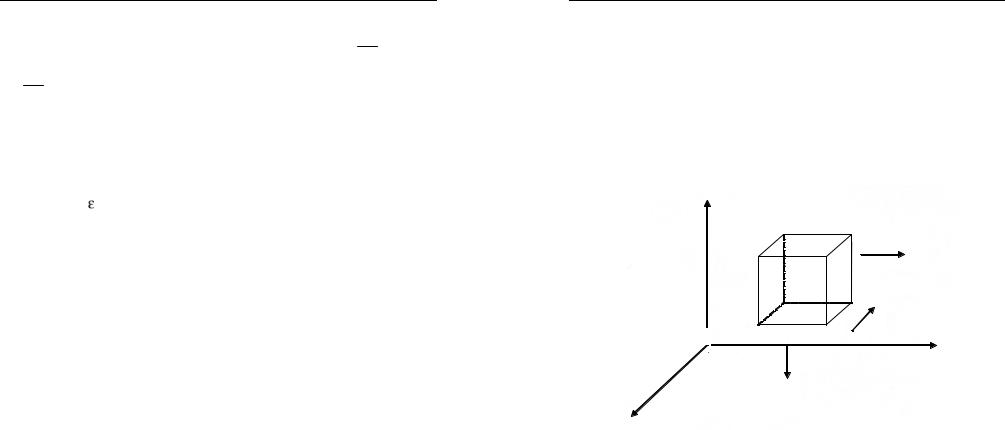
Выделим в теплопроводной среде элементарный кубик со сто- |
|||
ронами dx,dy,dz (рис. 1.2) и приведем подсчет изменения содержа- |
|||
щейся в нем тепловой энергии за малый промежуток времени ∆t . |
|||
По сделанным предположениям это изменение может быть вызвано |
|||
лишь разностью потоков тепла, входящих и выходящих через раз- |
|||
ные грани кубика. Так, потоки вдоль оси x приводят к уменьшению |
|||
или увеличению внутренней энергии объема на величину |
|||
[Wx (x,y,z,t)−Wx (x +dx,y,z,t)]dydzdt , |
где dy dz – площадь грани, |
||
перпендикулярной оси x . |
|
|
|
z |
|
|
|
|
|
Wy |
|
T(x,y,z) |
dz |
T (x,y + dy,z) |
|
dx |
|||
|
|||
|
|
||
|
dy |
Wx |
|
0 |
|
y |
|
|
Wz |
|
|
x |
|
|
|
Рис. 1.2. Компоненты потока тепла в элементарном |
|||
кубике теплопроводной среды |
|||
Вэтойформулесчитается,чтоWx какфункциявременинесиль-
но изменяется за промежуток dt , и можно взять ее значение в момент t . Точно таким же образом вычисляются изменения внутренней энергии по осям y,z :
[Wy (x,y,z,t)−Wy (x,y +dy,z,t)]dxdzdt ;
[Wz (x,y,z,t)−Wz (x,y,z + dz,t)]dydxdt .
Суммарное изменение энергии ∆E = E(t +∆t)− E(t) есть
∆E = −divWdxdydzdt .
10 |
11 |

Математическое моделирование и расчет элементов строительных конструкций
С другой стороны, величину ∆E можно выразить через изменение температуры объема и через его теплоемкость по формуле
∆E =[T (t +∆t)−T (t)]c(ρ,t)ρdxdydz, в которой из-за малости объема бе-
рутся некоторые средние по нему значения температуры и плотности. Приравнивая друг другу два последних выражения и устрем-
ляя dt к нулю, получим общее уравнение, описывающее распространение тепла,
C |
∂T |
= div(χgradT ), |
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеющее в развернутом виде вид |
|
|
|
|
|
|
|||||||||||
|
|
C |
∂T |
|
∂ |
∂T |
|
∂ |
∂T |
∂ |
|
∂T |
, |
(1.2) |
|||
|
|
∂t |
= |
|
χ |
|
+ |
|
χ |
+ |
|
|
χ |
|
|||
|
|
|
|
|
|||||||||||||
|
|
|
|
∂x |
∂x |
|
∂y |
∂y |
∂z |
|
∂z |
|
|
||||
где C = ρc .
Уравнение (1.2) – нестационарное, трехмерное уравнение параболическоготипа.Ононеоднородное, так кактеплоемкость, коэффициент теплопроводности и плотность могут быть, вообще говоря, разными в разных точках вещества, и нелинейное, поскольку функ-
ции с и χ могут зависеть от температуры T .
Есликуравнению(1.2)добавитьначальные икраевые условия, соответствующие рассматриваемой задаче описания процесса теплопередачи, то получим искомую математическую модель процесса.
Рассмотримвначаленекоторыечастныеслучаиуравнения(1.2). При дополнительных предположениях о характере процесса теплопередачи уравнение (1.2) можно упростить. Так, если процесс стационарный, т. е. температура не зависит от времени, то (1.2) превра-
щается в уравнение эллиптического типа |
|
|||||||||||||
|
∂ |
|
∂T |
|
∂ |
∂T |
∂ |
|
∂T |
= 0 |
, |
|||
|
|
|
χ |
|
+ |
|
χ |
+ |
|
|
χ |
|
||
|
|
|
|
|||||||||||
|
∂x |
|
∂x |
|
∂y |
∂y |
∂z |
|
∂z |
|
|
|||
а если функции c,χ не зависят от температуры, то (1.2) становится линейным параболическим уравнением, которое в случае однородной среды (χ,c,ρ не зависят от x,y,z ) принимает вид
∂T |
= k0∆T , |
(1.3) |
∂t |
|
|
Глава 1. Основы математического моделирования
где k0 = |
χ |
называется коэффициентом температуропроводности. |
|||||||||||||
|
|||||||||||||||
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||
Для уравнения (1.3) не трудно выписать общее решение. |
|||||||||||||||
В однородном случае (температура зависит лишь от t |
и x ) из |
||||||||||||||
(1.2) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
C |
∂T |
= |
|
∂ |
|
∂T |
|
|
|||
|
|
|
|
|
|
|
|
|
χ |
|
. |
(1.4) |
|||
|
|
|
|
∂t |
∂x |
|
|||||||||
|
|
|
|
|
|
|
∂x |
|
|
||||||
Уравнение (1.4) сводится к уравнению типа нелинейной тепло- |
|||||||||||||||
проводности |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∂U |
|
∂ |
|
|
∂U |
|
|||||
|
|
|
|
∂t |
|
= |
|
|
k(U ) |
∂x |
|
(1.5) |
|||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∂x |
|
|
|
|
|||||
при допущении, что |
∂C |
≡ 0 , |
∂χ ≡ 0. |
|
|
|
|
|
|||||||
∂x |
|
|
|
|
|
||||||||||
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
||
Наконец,если χ = χ0 , C = c0 ,где χ0 ,c0 –постоянные,тоиз(1.5) получается уравнение теплопроводности – простейшее уравнение
параболического типа |
|
|
|
∂U |
= k0 |
∂2U . |
(1.6) |
∂t |
|
∂x2 |
|
Из уравнения (1.2) можно получить различные обобщения, соответствующие более сложным, чем рассмотренные выше, механизмам теплопередачи. Так для неизотопной среды (т. е. когда коэффициенты теплопроводности разные по разным направлениям) с энерговыделением, вместо (1.2) имеем
C |
∂T |
|
∂ |
|
∂T |
|
∂ |
∂T |
|
∂ |
|
|
∂T |
|
|||
|
= |
|
|
χx |
|
+ |
|
χy |
|
+ |
|
|
|
χz |
|
+ |
|
∂t |
|
|
∂z |
||||||||||||||
|
|
∂x |
|
∂x |
|
∂y |
∂y |
|
|
|
∂z |
|
|||||
|
|
|
|
|
|
|
|
+ f (x,y,z,t,T ), |
|
|
|
(1.7) |
|||||
где χx ,χy ,χz – коэффициенты в законе Фурье (1.1) по осям x , y ,z ;
функция f – мощность выделения (или поглощения) энергии.
Все полученные в данном пункте уравнения выведены с помощью фундаментального закона сохранения энергии и закона Фурье. Вместе с заданными функциями χ,c,ρ начальными и краевыми ус-
12 |
13 |

Математическое моделирование и расчет элементов строительных конструкций
ловиями они представляют собой замкнутые математические модели процесса теплопередачи.
Рассмотримтипичныекраевыеусловиядляпроцессатеплопроводности. Для простотыбудемрассматривать одномерные процессы теплопроводности. Они имеют место, например, в длинном и тонком металлическом стержне (рис. 1.3), нагреваемом с одного из торцов, при условии, что стерженьизотропен, егоначальная температура в любом поперечном сечении не зависит от y,z, а потерями тепла с боковой поверхности можно пренебречь (в частности, она может быть теплоизолирована).
T |
(0,t) |
T (l,t) |
|
|
|
|
|
|
|
T (x,t) |
|
0 |
|
l |
x |
Рис. 1.3. Металлический стержень, нагреваемый с одного из торцов
Будемсчитатьтакже,чтотеплоемкостьстержняпостоянна.Тогда температура зависит только от x и t , и ее распределение вдоль стержня в различные моменты времени описывается уравнением
∂T |
|
∂ |
∂T |
|
|
∂t |
= |
|
k(T ) |
, |
(1.8) |
|
|||||
|
∂x |
∂x |
|
||
справедливым при 0 < x < l, t > 0.
Для определения функции T ( x , t ), т. е. решения уравнения (1.8),достаточнозадатьначальнуютемпературустержня(начальные условия по переменной t ):
T ( x , 0 ) =T 0 ( x ), 0 ≤ x ≤ l |
(1.9) |
изнатьтемпературунаконцахстержнявлюбоймоментвремени(краевые условия по переменной x ):
T (0 , t ) =T1 (t ), T (l , t ) =T 2 (t ), t > 0. |
(1.10) |
Задача (1.8)–(1.10) называется первой краевой задачей для параболического уравнения (1.8) на отрезке x [0 , l ].
Глава 1. Основы математического моделирования
Если же на концах стержня задаются вместо (1.10) потоки тепла как функции времени (другие краевые условия):
− k [T (0 , t )]∂T |
|
=W1 (t ), |
|||
|
|||||
|
∂x |
|
x=0 |
||
|
|
|
|
(1.11) |
|
k [T (l , t )] |
∂T |
|
|
|
=W 2 (t ), t > 0, |
|
|
||||
|
∂x |
|
|
x=l |
|
тотакаязадачаназываетсявторойкраевойзадачейнаотрезке[0 , l ].
Могут быть заданы и другие краевые условия.
Для многомерных уравнений теплопроводности постановка краевых условий по сравнению с одномерным случаем существенно не меняется: на границах области задаются либо температура, либо поток тепла, либо какие-то более сложные их комбинации. Кроме
того, задаетсяначальное распределениетемпературывмомент t = 0 (начальное условие).
В случае стационарного уравнения теплопроводности задаются только краевые условия.
1.4.2. Модели, получаемые совместным применением нескольких фундаментальных законов
Для построения математической модели, описывающей течение несжимаемого газа, используются законы сохранения массы, импульса, энергии.
Рассмотрим некоторые понятия газовой динамики. Заметное изменение плотностей жидкостей и твердых тел может достигаться лишь при огромных давлениях в десятки и сотни тысяч атмосфер и выше.
Газообразные среды гораздо легче подвергаются сжатию: при перепаде давления в одну атмосферу плотность газа, первоначально находящегося при атмосферном давлении, уменьшается или увеличивается на величину, сопоставимую с ее начальной плотностью.
Вгазовойдинамике,изучающейдвижениесжимаемыхсредпод действием каких-либо внешних сил или сил давления самого вещества,считаетсявыполненнымнеравенство λ << L, где λ –длинасво-
14 |
15 |
Математическое моделирование и расчет элементов строительных конструкций
бодного пробега, L – характерные размеры области рассматриваемого течения (сплошная среда). Считается также выполненной гипотеза о локальном термодинамическом равновесии (см. 1.4.1). Вусловияхлокальноготермодинамическогоравновесиясжимаемую среду можно рассматривать как совокупность большого числа жид-
ких частиц с размерами, много большими λ, но много меньшими L . Для каждой такой частицы, связанной с небольшой фиксированной массой среды, вводятся характеризующие ее средние величины –
плотность ρ, давление P , температура T , внутренняя энергия ε
ит. д., а также скорость v ее макроскопического движения как единого целого. Все эти величины в общем случае зависят от трех пространственных координат x,y,z и времени t .
Вдальнейшем будем также предполагать отсутствие в среде процессовтеплопередачи,вязкоготрения, источниковистоковэнергии, например, излучения, и отсутствие внешних объемных сил
иисточников (стоков) массы в веществе.
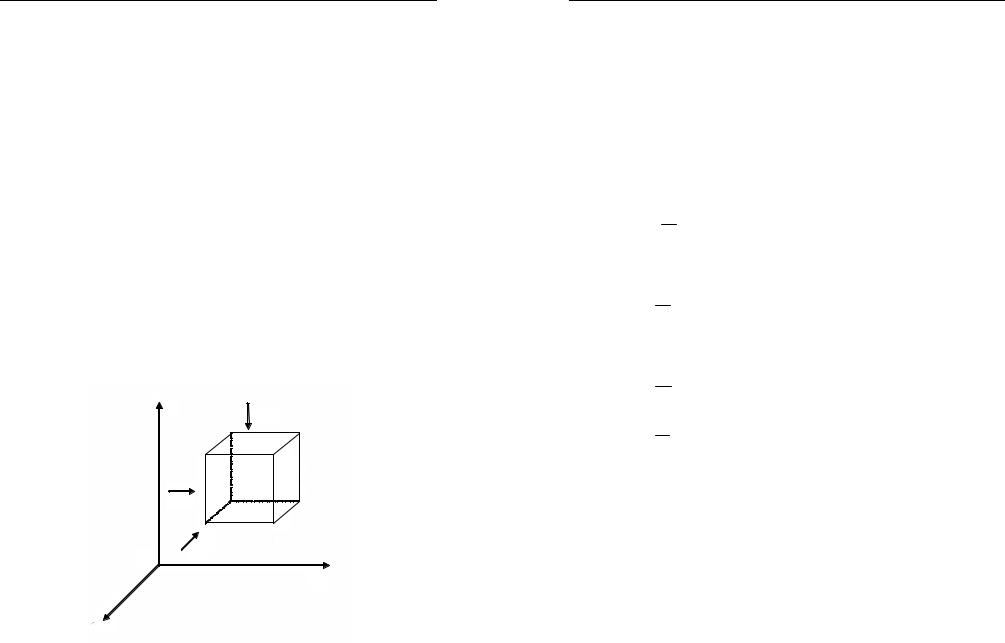
Получим уравнения неразрывности (сплошности) для сжимаемого газа. Рассмотрим в некоторой области пространства, занятой
движущимся газом, элементарный кубик со сторонами dx,dy,dz и подсчитаем в нем баланс массы за время dt (рис. 1.4).
z |
ρvz |
|
dz |
|
ρv y |
|
dx |
|
dy |
|
ρvx |
0 |
y |
|
x
Рис. 1.4. Элементарный кубик с движущимся газом
Глава 1. Основы математического моделирования
Здесь vx ,vy ,vz – компоненты скорости по соответствующим осям.
По оси x через грань с координатой x в кубик за время dt поступаетмассагаза,равная ρvxdydzdt , посколькувеличина ρvx не что иное как поток массы по направлению оси x . За то же самое время из грани с координатой x +dx вытекает масса [ρvx +d(ρvx )]dydzdt, где через d(ρvx ) обозначено приращение потока массы при перехо-
де от координаты x к координате x +dx. Суммируя оба последних выражения и учитывая, что
d(ρvx ) = ∂∂x (ρvx )dx ,
получаемвеличинуизменения массывкубике за время dt благодаря движению газа вдоль оси x :
dmx = −∂∂x (ρvx )dxdydzdt.
Точно таким же образом находим изменение массы за счет движения по осям y,z :
dmy = −∂∂y (ρvy )dxdydzdt ,
dmz = −∂∂z (ρvz )dxdydzdt.
Вфиксированномобъемекубика изменениенаходящейсявнем массы газа выражается также черезизменение его плотностисо вре-
менем: |
|
|
|
dm = |
∂ρdtdxdydz. |
|
|
|
∂t |
|
|
Суммируя dmx ,dmy ,dmz |
и приравнивая результат к dm, полу- |
||
чим искомое уравнение неразрывности |
|
||
|
∂ρ |
+div ρv = 0 , |
(1.12) |
|
∂t |
|
|
выражающее закон сохранения массы вещества применительно к движению сжимаемого газа.
16 |
17 |
Математическое моделирование и расчет элементов строительных конструкций
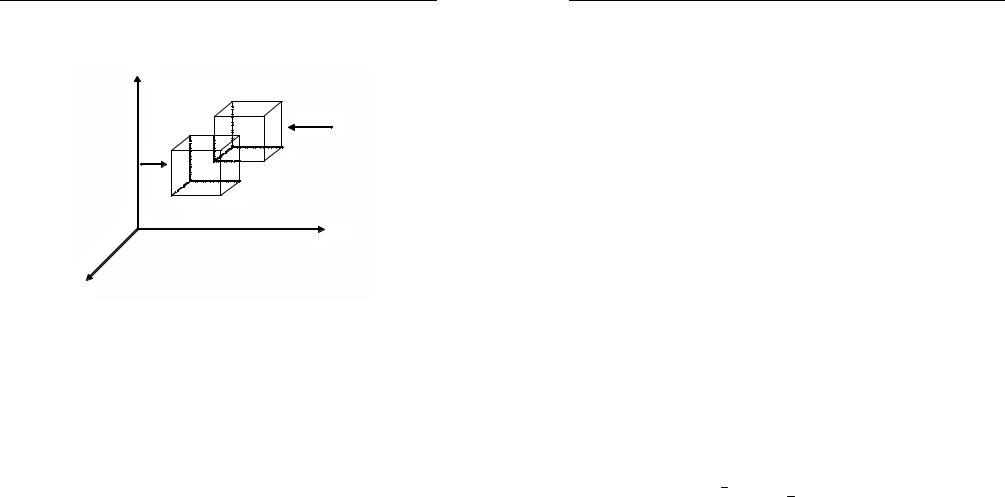
Теперьполучимуравнениядвижения газа.Дляэтогоприменим второй закон Ньютона к элементарной жидкой частице, имеющей
в некоторый момент t форму кубика с гранями dx,dy,dz (рис. 1.5).
z
|
|
t + dt |
P(y + dy) |
|
|
|
|
|
t |
|
|
|
P(y) |
|
|
|
dz |
|
dx |
|
|
dy |
|
|
|
|
|
0 |
|
|
y |
x
Рис. 1.5. Перемещающаяся в пространстве жидкая частица, имеющая объем кубика
Жидкая частица – это перемещающийся в пространстве и меняющий свою форму объем, содержащий в разные моменты време-
ни t одни и те же атомы и молекулы газа. Тем самым его масса dm постоянна. Для простоты вывода уравнений будем считать, что за
короткоевремя dt кубикнеменяетсвоейформыисмещаетсяповсем направлениям на расстояние, много меньшее его размерам.
Определим сначала силу, действующую на кубик, например, в направлении оси y . Она, очевидно, равна разности давлений на левой и правой гранях, умноженной на их площади (иных сил по предположению нет):
Fy =[P(x,y,z,t)− P(x,y +dy,z,t)]dxdz. |
(1.13) |
|||
Сила Fy равна ускорению жидкой частицы в направлении y , |
||||
умноженному на ее массу dm = ρdxdydz : |
|
|||
Fy = |
dvy |
ρdxdydz . |
(1.14) |
|
dt |
||||
|
|
|
||
Глава 1. Основы математического моделирования
Заменяя в первом выражении для Fy (1.13) разность давлений
черезпроизводнуюотдавленияпо y иприравниваяегок(1.14),приходим к уравнению, описывающему движение газа вдоль оси y :
ρ |
dvy |
= − |
∂P |
. |
(1.15) |
|
dt |
∂y |
|||||
|
|
|
|
Точно так получим уравнения движения по направлениям x,z :
ρ |
dvx |
= − |
∂P |
; |
|
|
∂x |
|
|||
|
dt |
|
|
|
|
ρdvz |
= − |
∂P . |
(1.16) |
||
|
dt |
|
∂z |
|
|
В векторной форме уравнения (1.15), (1.16) имеют вид |
|||||
ρdv |
= −gradP. |
(1.17) |
|||
|
dt |
|
|
|
|
Поясним, что в (1.15)–(1.17) через |
df |
обозначена полная (суб- |
|||
|
|
|
|
dt |
|
станционная,т.е.связаннаяс фиксированнымичастицамигаза)производная по времени какой-либо величины, характеризующей данную неизменную массу газа.
Раскрыв |
df |
через частные производные по x и t |
в соответ- |
|||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ствии с правилом |
df = |
∂f |
+(vgrad)f , придем к уравнениям движе- |
|||||||||||||||
ния Эйлера: |
|
|
|
dt |
∂t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
v |
|
|
|
|
|
|
1 gradP. |
|
|
|
|
|||
|
|
|
|
+(vgrad) |
v |
= − |
|
|
|
(1.18) |
||||||||
|
|
|
|
∂t |
|
|
|
|
ρ |
|
|
|
|
|
||||
Будучи записаны покоординатно, они принимают вид |
||||||||||||||||||
|
|
∂vx + vx |
∂vx |
|
+vy |
∂vx |
+vz |
∂vx |
= − |
1 ∂P |
; |
|
||||||
|
|
∂t |
|
|
∂x |
|
|
∂y |
|
|
∂z |
|
ρ ∂x |
|
|
|||
|
|
∂vy |
|
+vx |
∂vy |
|
+vy |
∂vy |
+vz |
|
∂vy |
= − |
1 ∂P |
; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂t |
∂x |
∂y |
|
∂z |
ρ ∂y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
∂vz |
+vx |
∂vz |
+vy |
∂vz |
+vz |
|
∂vz |
= − |
1 |
∂P |
. |
(1.19) |
||||
|
|
|
|
∂y |
|
∂z |
|
|||||||||||
|
|
∂t |
|
|
∂x |
|
|
|
|
|
ρ ∂z |
|
|
|||||
18 |
19 |
