Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013

.pdf

Скачиваний:

336

Добавлен:

12.03.2016

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Математическое моделирование и расчет элементов строительных конструкций

Послеаналогичногопреобразованиявсехчленоввариационного уравнения(1.43)получим,исходяизтого,что δU ,δV ,δW произвольны в области, занимаемой пластинкой, уравнения равновесия

∂N

x +

∂Nxy

= 0,

∂N y

∂Nxy

∂y

∂x

∂2W + N y ∂2W

+2Nxy

∂2W

∂x2

∂y2

∂x∂y

∂2M

∂2 M xy

∂2 M y

+q = 0.

(1.47)

∂x2

∂x∂y

∂y2

Для получения замкнутой математической модели деформирования пластины, допускающей прогибы, соизмеримые с толщиной пластины (геометрически нелинейная постановка), к уравнениям равновесия (1.47) необходимо добавить краевые условия на контуре пластины.

При шарнирно-неподвижном закреплении контура пластины краевые условия принимают вид:

при x = 0, x = a

U =V =W = 0,	∂2W		= 0;			(1.48)
	∂x2
при y = 0, y = b
U =V =W = 0,		∂ 2 W		=	0.	(1.49)
U =V =W = 0,		∂y 2		=	0.

1.11. О нелинейности математических моделей

Большинство реальных процессов и соответствующих им математических моделейнелинейны. Линейные же моделиотвечают весьма частным случаям и, как правило, служат лишь первым приближением к реальности. Однако линейные модели в некоторых случаях могутадекватно отражать реальный процесс (например, многие строительные конструкции деформируются по линейным законам).

Глава 1. Основы математического моделирования

Для линейных моделей справедлив принцип суперпозиции, т. е. любая линейная комбинация решений также является решением задачи. Пользуясь принципом суперпозиции, нетрудно, найдя решение в каком-либо частном случае, построить решение в более общей ситуации. Именно из-за своей простоты линейные модели наиболее привлекательны.

Для нелинейных явлений, математические модели которых не подчиняются принципу суперпозиции, знание о поведении части объекта еще не гарантирует знания поведения всего объекта, а его отклик на изменение условий может качественно зависеть от величины этого изменения.

Источникаминелинейностимогутбытьмногиефакторы.Фундаментальные законы природы – законы тяготения и законы Кулона – изначально нелинейны, и поэтому основанные на них модели также нелинейны. Свой вклад в нелинейность вносят изменение характера взаимодействия в самом объекте при изменении его состояния, различные внешние воздействия и др.

В сущности, реальным явлениям отвечают только нелинейные модели, а линейные справедливы лишь при описании незначительных изменений величин, характеризующих объект.

Математическое моделирование и расчет элементов строительных конструкций

Глава 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЕФОРМИРОВАНИЯ ЭЛЕМЕНТОВ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ

2.1. Основные характеристики напряженно-деформированного состояния конструкции

Целью расчета и проектирования конструкций любой сложностиявляетсяобеспечениепрочностиижесткостиэтихконструкцийпри минимальных расходах материала. Поэтому при расчете элементов конструкций желательно получить наиболее точное решение поставленной задачи. Это возможноприучете различныхсвойствматериала конструкции для описания напряженно деформированного состояния конструкции и наиболее точного решения уравнений равновесия.

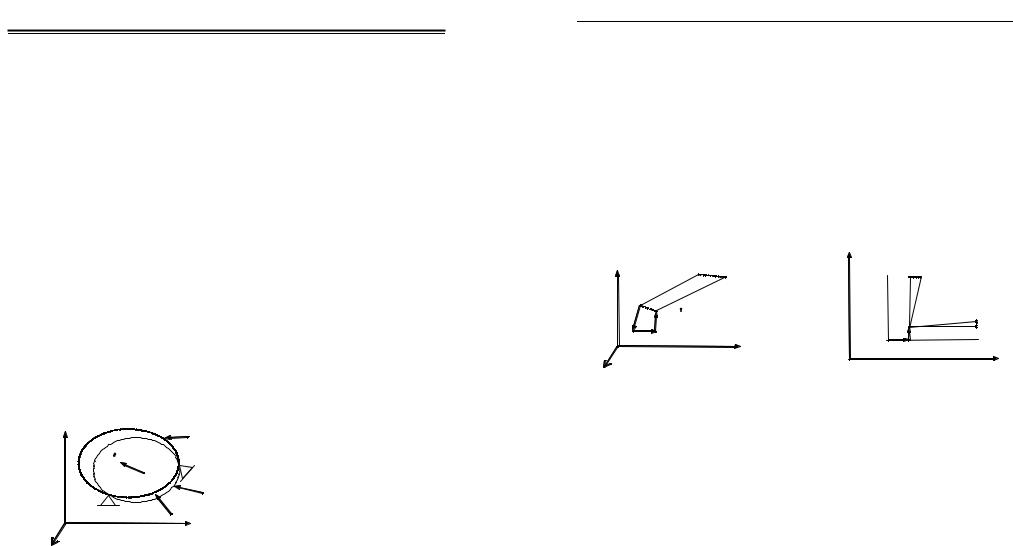
Пусть на трехмерное тело, закрепленное определенным образом (невозможно смещение тела как единого целого), действуют нагрузки P1,P2 , ,Pn (рис. 2.1).Действующие внешние силыдеформируют тело [2]. Изменение формы тела связано с перемещениями его

z			точек. Каждая точкаA,имеющая
z		P1	координаты x, y, z до деформа-
		P1

	A′		ции, в результате деформации
	A	Pn	перемещается в новое положе-
	P2	Pn	ние A' с координатами
0 x	P2	y	(x +u,y +v,z + w).
0 x		y	Приращения u, v, w коор-
Рис. 2.1. Перемещение точек тела			динат точки A называются ком-
Рис. 2.1. Перемещение точек тела			понентами перемещений этой

точки вдоль осей 0x, 0y, 0z. Компонентыперемещений зависятот координат точки u(x, y, z), v(x, y, z), w(x, y, z) и являются непрерывными функциями. Перемещения измеряются в метрах.

В результате перемещений точек возникают деформации – относительные удлинения отрезков и изменения угловых величин.

Глава 2. Математические модели деформирования элементов строительных...

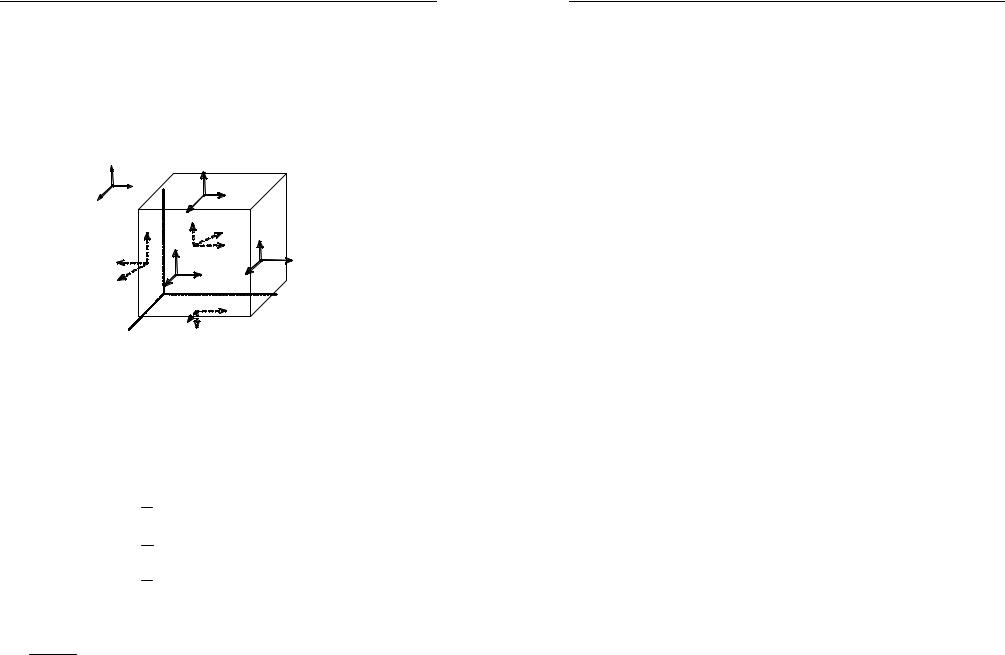
Относительныеудлинениябесконечномалыхотрезковdx,dy,dz , которые до деформации были параллельны осям координат 0x, 0y, 0z,равныдеформациямудлинения εx ,εy ,εz (продольныеилилинейные деформации). Изменения первоначально прямых углов между линейными элементами dx,dy,dz в соответствующих плоскостях равны деформациям сдвига γxy ,γyz ,γzx (рис. 2.2). Деформации являются безразмерными величинами.

Шестьвеличин, εx , εy , εz , γxу, γyz , γzx ,достаточнодлятого,чтобыопределить линейные и угловые деформациивданной точке тела в любых направлениях. Эти величины называются компонентами деформаций.

z		B	B’	y	∂u dx
	ds	B	B’		∂y
	ds

A	ds*			(1 + εy )dy
u	wA′			v	(1 + εx )dx	∂v dy
0	v	y		v	(1 + εx )dx	∂x
0		y	0	u		x
x			0			x

Рис. 2.2. Изменение линейных и угловых величин в результате деформирования

Деформации выражаются через перемещения геометрическимисоотношениями,впростейшемслучаеэтосоотношенияКоши[2]:

εx = ∂∂ux ; γ xy

εy = ∂∂yv ;γ yz

εz = ∂∂wz ;γ zx

=∂∂uy + ∂∂vx ;

=∂∂vz + ∂∂wy ;

=	∂w	+	∂u .	(2.1)
	∂x		∂z

Формулами (2.1) можно пользоваться в тех случаях, когда удлинения, сдвиги и углы поворота малы по сравнению с единицей, а квадратичные комбинации углов поворота малы по сравнению с компонентами деформаций.

Для того чтобы численно характеризовать степень воздействия внешних сил на деформированный элемент, вводится понятие напря-

Математическое моделирование и расчет элементов строительных конструкций

жения. Напряжение– силовой фактор,представляющийсобой интенсивность действия внутренних сил,приходящихсяна единицуплощади, выделенную в какой-либо точке рассматриваемого сечения.

В направлении осей 0x, 0y, 0z действуют нормальные напряжения σx ,σy ,σz ,связанныесдеформациямирастяжения-сжатия.Вплос-

костях x0y, x0z, y0z появятся напряжения сдвига τxу,τyz ,τxz , связанные с деформациями сдвига (рис. 2.3). Напряжения измеряются

в мегапаскалях (МПа).

z	σz
	y
x	τxz	τyz
	τxz	τyz
	τxz	τyz
	τxz
	τxy	σ y
	τxy	τyx
	σx

Рис. 2.3. Правило знаков для напряжений

Компонентынапряженийсвязаныскомпонентамидеформаций соотношениями, которые называют физическими соотношениями, вид которых зависит от проявляемых свойств материала (упругие, пластические, свойства ползучести и т. д.). Для упругого тела эта зависимость выражается законом Гука. В случае сложного напряженного состояния справедлив обобщенный закон Гука:

εx = E1 [σx −µ(σy + σz )],

εy = E1 [σy −µ(σz + σx )],

εz = E1 [σz −µ(σx +σy )],

εxy =	τxy			;
	τGyz
εyz =			;
	τGzx
εzx =		,			(2.2)

	G

где E – модуль упругости материала; μ – коэффициент Пуассона;

G = 2(1E+ µ) – модуль упругости второго рода, или модуль сдвига.

Глава 2. Математические модели деформирования элементов строительных...

Следующую группу соотношений составляют уравнения равновесия, которые могут быть получены из условия минимума функционала полной энергии деформации тела.

Функционал полной энергии деформации равен разности потенциальной энергии системы П и работы внешних сил А, т. е.

Э = П− А.

(2.3)

Для трехмерного тела (V) потенциальная энергия записывается в виде [2]:

П = 12	∫∫∫(σxεx +σyεy +σz εz + τxy γxy + τxz γxz + τyz γyz )dV . (2.4)
	V

Таким образом, математическая модель деформирования любой конструкции состоит из трех групп соотношений: геометрических, связывающих деформации и перемещения; физических, связывающих напряжения и деформации; функционала полной энергии деформации системы, который может быть представлен через интеграл от искомых функций перемещений:

Э = ∫∫∫Ф(u ,v ,w )dV .

2.2. Геометрические соотношения для элементов строительных конструкций

Элементы строительных конструкций – балка (стержень, рабо- тающийнаизгиб),плита(пластина),оболочка–представляютсобой трехмерные тела. Чтобы упростить нахождение всех характеристик напряженно-деформированногосостоянияконструкций,используют ряд гипотез. В результате их использования, зная характеристики деформирования координатной линии для стержня, координатной плоскостидляплиты,координатнойповерхностидляоболочки,можнонайтихарактеристикидеформированияконструкциивлюбомслое, отстающем на z от координатного.

Основными являются гипотеза плоских сечений для балок, согласно которой все сечения, нормальные к оси балки в ее недеформированном состоянии, остаются плоскими (не искажаются) и сохраняют свою перпендикулярность к оси балки в процессе ее изги-

Математическое моделирование и расчет элементов строительных конструкций

ба; гипотеза прямых нормалей для пластин и оболочек, согласно которой прямолинейные отрезки, которые до деформации были перпендикулярны к срединной по-

	x	верхности, при деформирова-
	x	нииостаютсяпрямолинейными
	x	и нормальными к деформиро-
	Рис. 2.4. Деформация элемента со-	и нормальными к деформиро-
	Рис. 2.4. Деформация элемента со-	ванной срединной поверхности
	гласно гипотезе плоских сечений	(рис. 2.4).

Согласно гипотезе прямой нормали, перемещения в слое, отстоящем на z от срединной поверхности пологой оболочки, будут

линейно зависеть от z
u z	= u − z ∂w ,	vz	= v − z ∂w ,	w	z	= w	.	(2.5)
	∂x		∂y	w		= w
Здесь u(x,y), v(x,y), w(x,y) – перемещения точек срединной
поверхности вдоль координатных осей				x ,		y , z соответственно;
u z (x,y), vz (x,y),	wz (x,y) – перемещения вдоль соответствующих
осей в слое, отстоящем на z от срединной поверхности.
			Для стержня,					работающего
q(x)			только на изгиб (рис. 2.5), переме-
		x	щениями u , v срединной линии
0	l	x	пренебрегаем, перемещения w
z			оказываются функциями только
Рис. 2.5. Балка с распределен-			однойкоординаты w = w ( x ), в ре-
ной нагрузкой			зультате учитываем только дефор-
мации ε xz , для которых имеем соотношение
	εxz	= du z = z χ,						(2.6)
где			dx
где
			d 2 w
	χ = − dx2 .							(2.7)

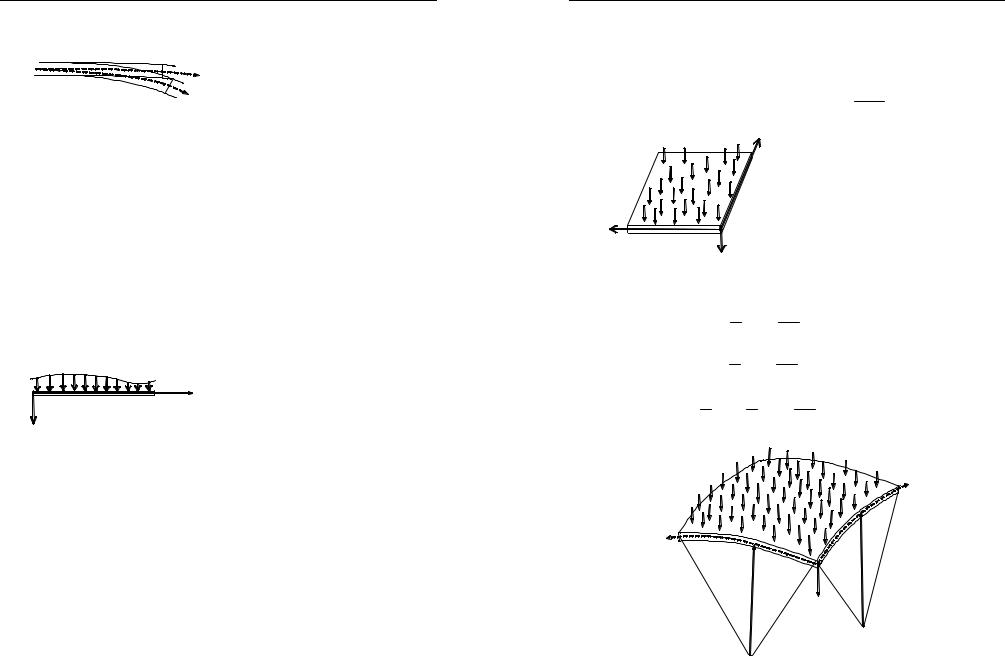
Для плиты, работающей только на изгиб (рис. 2.6), внутренними усилиями Nx , N y , Nxy пренебрегаем и для деформаций имеем соотношения

Глава 2. Математические модели деформирования элементов строительных...

∂u z

= zχ

∂vz

= zχ2 ,

∂u z

∂vz

= 2zχ12 ,

(2.8)

∂x

, εy =

∂y

γxy =

∂y

∂x

где

χ1 = −∂2 w , χ2 = −

∂2w2

, χ12 = −

∂2 w

–

(2.9)

∂x2

∂y

∂x∂y

функции изменения кривизны

и кручения.

q(x, y)

Дляоболочекобщеговида

учитывается сложное напря-

женное состояние (рис. 2.7)

и деформации координатной

поверхности (геометрически

линейнаятеория,модельКирх-

Рис. 2.6. Плита, нагруженная

гофа – Лява) имеют вид [16]

распределенной нагрузкой

ε x

1 ∂u

1 ∂A v −k x w ;

A ∂x

AB ∂y

ε y

1 ∂v

1 ∂B u − k y w ;

B ∂y

AB ∂x

∂v

∂u

∂A

∂B

γ xy

−

(2.10)

∂x

∂y

∂x

q(x,y)

Рис. 2.7. Оболочка, находящаяся по действием распределенной нагрузки

Математическое моделирование и расчет элементов строительных конструкций

Здесь A, B – параметры Лямэ, характеризующие поверхность оболочки (дляразличныхвидовоболочек –пологихпрямоугольного плана, цилиндрических, конических, сферических и т. д. – они име-

ютразличныезначения);функциикривизны kx =	1	, k y =	1	–глав-

	R1		R2

ные кривизныоболочки вдоль осей x и y ; R1, R2 –главныерадиусы

кривизны в направлении координат x и y .

В слое, отстоящем на z от срединной поверхности оболочки, деформации принимают вид

εz

= ε

+ zχ

, εz = ε

+ zχ

, γz

= γ

+2zχ ,

(2.11)

где

χ = −

1 ∂

1 ∂w

−

∂A

1 ∂w

;

B ∂y

A ∂x

∂x

∂y

1 ∂

1 ∂w

∂B

1 ∂w

χ2 = −

−

;

A ∂x

B ∂y

∂y

∂x

2χ12 = −

1 ∂

1 ∂w

−

∂

1 ∂w

A ∂x

B ∂y

∂y

∂x

∂A

1 ∂w

∂B

1 ∂w

(2.12)

∂x

B ∂y

∂y

∂x

Для пологой оболочки прямоугольного плана, когдаA = B =1, соотношения (2.10) и (2.12) упрощаются и принимают вид (2.60) и (2.61).

2.3. Физические соотношения для элементов строительных конструкций при линейно-упругом деформировании

При линейно-упругом деформировании физические соотношения, связывающие компоненты напряжений с компонентами деформаций, задаются законом Гука.

Физические соотношения: для стержня

σx = Eεxz = Ezχ;

(2.13)

Глава 2. Математические модели деформирования элементов строительных...

для пластин

σx = 1 −Eµ2 [εzx +µεzy ]= 1 −Ezµ2 [χ1 +µχ2 ]; σy = 1 −Eµ2 [εzy +µεzx ]= 1 −Ezµ2 [χ2 +µχ1];

γz

(2.14)

2(1+µ)

1+µ

12 ,

для оболочек

σx =

[εxz +µεzy

[εx +µεy + z(χ1 +µχ2 )];

1−µ

σy =

[εzy +µεxz

[εy +µεx

+ z(χ2

+µχ1)]

1−µ2

;

γz

[γ

+2zχ

]

(2.15)

2(1+µ)

12 .

Здесь E – модуль упругости материала стержня; μ – коэффициент Пуассона.

2.4. Усилия и моменты для элементов строительных конструкций при линейно-упругом деформировании

В качестве внутренних силовых факторов рассматриваются внутренние усилия – интегралы по переменной z от напряжений и изгибающие моменты – интегралы по переменной z от напряжений, умноженных на z.

Для балки прямоугольно-	M (x)	M (xx +dx)
го сечения высотой h и шири-		M (xx +dx)
го сечения высотой h и шири-	z	dx
ной b единственным внутрен-		dx
ной b единственным внутрен-
ним силовым фактором явля-	Рис. 2.8. Направления изгибающих
ются изгибающий момент	моментов в сечениях балки
(рис. 2.8)
h /2
M = ∫σxb zdz = EbI χ,		(2.16)

−h /2

Математическое моделирование и расчет элементов строительных конструкций

где

h /2
I = ∫z2dz .	(2.17)

−h /2

Если поперечную нагрузку q(x) задавать в МПа (на единицу площади), то ширину поперечного сечения стержня в (2.16) можно

не учитывать, т. е.
M = EI χ.		(2.18)
Для пластины, работающей только на изгиб, напряжения σx ,
σy , τxy создают изгибающие M x ,	M y	и крутящие M xy = M yx мо-
менты (рис. 2.9).
z
M yx	M xy
y		x
M y		M x

Рис. 2.9. Положительные направления изгибающих и крутящих моментов в сечениях плиты

Указанные моменты, приведенные к координатной поверхности и приходящиеся на единицу длины сечения, равны

h /2

(χ1 +µχ2 );

M x = ∫σx z dz =

12(1−µ

)

−h /2

h /2

(χ2 +µχ1 );

M y = ∫σy z dz =

(2.19)

12(1−µ

)

−h /2

h /2

Eh3

M xy = ∫τxy z dz =

χ12 .

12(1

+µ)

−h /2

Для оболочки, когда учитывается сложное напряженное состояние, для нормальных сил Nx , N y , касательных сил N xy = N yx ,

Глава 2. Математические модели деформирования элементов строительных...

изгибающих моментов M x , M y и крутящих моментов M xy = M yx (рис. 2.10), будем иметь соотношения

h /2

Eh2 (εx +µεy );

Nx = ∫σx dz =

−h /2

1−µ

h / 2

Eh2 (εy +µεx );

N y = ∫σy dz =

−h / 2

1−µ

h / 2

Nxy =

∫τxy dz =

γxy ;

−h / 2

2(1+µ)

h / 2

Eh3

(χ1 +µχ2 );

(2.20)

M x = ∫σx z dz =

12(1−µ

)

−h / 2

h /2

z dz =

Eh3

(χ2 +µχ1);

M y = ∫σy

12(1

−µ

)

−h / 2

h /2

Eh3

χ12 .

M xy =

∫τxy z dz =

12(1+µ)

−h /2

M x

M y

Nxy

M xy Nx

M yx

Nyx

Рис. 2.10. Направления внутренних усилий

в сечениях оболочки

Размерность усилий – МПа м, размерность моментов –

МПа м2 .

2.5. Физические соотношения для элементов строительных конструкций при нелинейно-упругом деформировании

Для различных материалов проводятся испытания на растяжение образцадлиной l ,площадьюпоперечногосечения F , нагруженного силой P (рис. 2.11).

и напряжение

Математическое моделирование и расчет элементов строительных конструкций

Рис. 2.11. Образец испытания

Для разного значения P определяют приращение l и находят относительное удлинение

стержня ε = ∆ll

σ = FP , по которым строят кривую «σ – ε» (рис. 2.12). [14].

		Характерными точками ди-
σ		аграммы являются предел упру-
		гости материала σу – наиболь-
σт		шее напряжение, до которого
σ у		имеет место прямая пропорцио-
σ у		нальная зависимость между на-
		нальная зависимость между на-
α		пряжением и деформацией
α	ε	σ = E ε, где E = tg α – модуль уп-
	ε	σ = E ε, где E = tg α – модуль уп-
		ругости материала. Следующая
Рис. 2.12. Зависимость «σ−ε»		характернаяточка–пределтеку-
		чести материала σт.

Исходя из кривой «σ–ε», полученной для различных материалов опытным путем, следует, что только при σ<σу конструкция деформируется линейно-упруго. Также существуют материалы, для

		которых отсутствует линейный
σ		участок этой зависимости
	B	(рис. 2.13). Причем процесс де-
	A	формирования при нагружении
	A	происходит по кривой ОAB. Для
		происходит по кривой ОAB. Для
		учета этого факта (физической
β	ε	нелинейности)замодуль упруго-
β	ε	сти принимают секущий модуль
O	C	сти принимают секущий модуль
O	C	упругости E с = tgβ.Кривую σ(ε)
Рис. 2.13. Определение секущего		упругости E с = tgβ.Кривую σ(ε)
Рис. 2.13. Определение секущего		аппроксимируют некоторой ана-
	модуля упругости	литической зависимостью, беря
		литической зависимостью, беря

вместо ε интенсивностьдеформаций εi , авместо σ –интенсивность напряжений σi .

Глава 2. Математические модели деформирования элементов строительных...

А. А. Ильюшиным [7] было предложено секущий модуль брать в виде

E =	σi = E(1−ω(ε		))	,	(2.21)
c	ε	i		,	(2.21)
		i

где ω(εi ) – некоторая функция, имеющая различный вид для разных материалов.

Например, для металлов и старого	бетона можно принять
ω(εi ) = mεi2 ,	(2.22)

где m – опытная константа.

Если учитывается только физическая нелинейность, то считается, чтои процессразгрузки протекает покривой ВАО. Однако для некоторых материалов процесс разгрузки протекает по прямой BC и после снятия нагрузки могут появиться остаточные или пласти-

ческие деформации εп = OC . При этомза модульупругости прираз-

грузке берется первоначальный модуль упругости E .

Существуетнесколькотеорийпластичности[7, 11,14].Однуиз них, деформационную теорию, можно использовать при рассмотрении нелинейно-упругого деформирования (физически нелинейная задача). При этом процесс разгрузки не рассматривается и пластическая деформации не исследуются.

Физические соотношения при учете физической нелинейности для стержня принимают вид

σx = Ec εxz

= Eεxz

−Eω(εi )εxz ,

(2.23)

или

= σУ

−σП,

(2.24)

где σуx задано соотношением (2.13), а σпx записывается в виде

σПx

= E ω(εi )εxz .

(2.25)

Здесь

εi =

εxz

zχ

–

(2.26)

интенсивность деформаций для стержня.

Математическое моделирование и расчет элементов строительных конструкций

Для плиты, работающей только на изгиб, в соответствии с деформационной теорией имеем

σx = σУx −σПx , σy = σУy −σПy , τxy = τУxy −τПxy ,

(2.27)

где σУx , σУy , τУxy –линейно-упругиесоставляющиенапряжений(фор- мулы (2.14)), а составляющие с индексом «П» примут вид

σПx =

Eω(ε2i )[εxz

+µεzy ]

= Ezω(ε2i )(χ1 +µχ2 );

1−µ

σП = Eω(εi )[εz

+µεz ]

Ezω(εi )(χ

+µχ )

;

1−µ2

τП

Eω(εi )

γz =

Ezω(εi )

(2.28)

2(1+µ)

12 –

пластические составляющие напряжений.

Интенсивность деформаций для плиты имеет вид

εi =

(εxz )2

+ εxz εzy

+ (εzy )2 +

1 (γxyz

(2.29)

Дляоболочкивсоответствии сдеформационнойтеориейфизи-

ческие соотношения будут иметь вид (2.27), где σуx ,

σуy , τуxy можно

представить в виде (2.15), а σп, σп

, τп

заданы соотношениями

σп

Eω(εi )

(ε

+µε

+ z(χ +µχ

))

1−µ2

;

σп

Eω(εi )(ε

+µε

+ z(χ

+µχ ))

;

1−µ2

τп

Eω(εi )

(γ

+2zχ )

(2.30)

2(1+µ)

2.6. Физические соотношения для элементов строительных конструкций при учете ползучести материала

При длительном нагружении в материале строительной конструкции может проявиться свойство ползучести – изменение деформаций со временем при постоянной нагрузке [10, 14, 23].

Глава 2. Математические модели деформирования элементов строительных...

В результате испытания над образцами из различных материа-

лов при постоянной нагрузке P и длительном времени ее воздействия строиться кривая «ε – t » ползучести материала (рис. 2.14),

где ε0 – мгновенная деформация в момент времени t = t0 .

	Существует несколько	ε
	теорий ползучести. Для плас-	ε
	тмасс и старого бетона можно
	использовать линейную тео-	ε0
	рию наследственной ползуче-	0
	сти. В металлах ползучесть
	может проявиться только при	t
	больших температурах.
	Будемрассматриватьква-	Рис. 2.14. Кривая ползучести
	зистатическую задачу, когда	Рис. 2.14. Кривая ползучести
	зистатическую задачу, когда

искомые функции зависят не только от координат x и y , но и от времени t , при этом инерционными членами можно пренебречь.

На основании линейной теории наследственной ползучести

вфизическихсоотношенияхпоявятсяинтегралывида ∫ε(τ)R1(t,τ)dτ,

∫γ(τ)R2 (t,τ)dτ.Здесь R1(t,τ) , R2 (t,τ) –функциивлиянияприрастя-

жении (сжатии) и сдвиге, зависящие от материала конструкции, которые находят из кривой «ε – t ». Например, для оргстекла [12]

R (t,τ) = A e−βi (t−τ)(t − τ)αi −1;				i =1,2;
i	i
A = 0,0269;	β = 0,045 10−3;			α = 0,05;
1	1			1
A = 0,013184; β		2	= 0,833 10−3	; α	2	= 0,2.	(2.31)
2		2			2

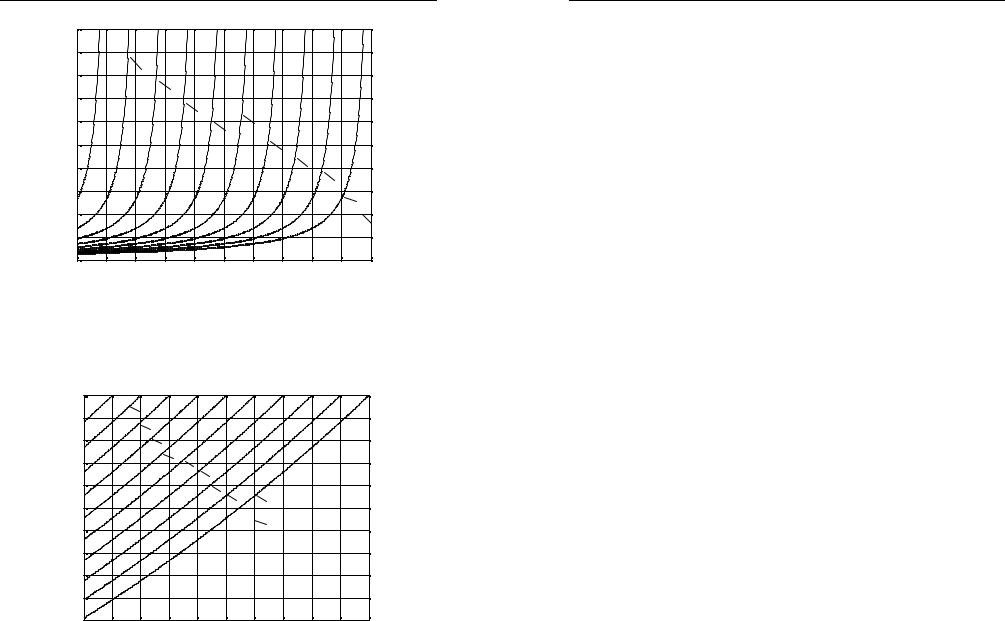
На рис. 2.15 представлены функции R1(tk ,τ) (2.31) для момен-

тов времени tk = k,сут.

Для старого бетона [3, 22, 28]

Ri (t,τ) = γ iE Ci∞ e				−γ(1+ECi∞ )(t−τ)		,i =1,2	;	(2.32)
γ	1	= 0,01;	E C		= 3, R2 = 2 R1.
	1			1∞		3
						3

Математическое моделирование и расчет элементов строительных конструкций
	0.1
	0.09
	0.08			1
	0.08
	0.07			2
	0.07				3
	0.06				3			5
								5
							4
	0.05						4	6
R	0.05							6
	0.04								7
	0.04									8
										8
	0.03										9
	0.02										9
	0.02
	0.01										10
	0.01
	00	1	2	3	4	5	6	7	8	9	10
						τ [сут]					τ сут
	Рис. 2.15. Вид функции влияния R1 для оргстекла:
кривая 1 соответствует функции R1(t1,τ); кривая 2 – R1(t2,τ) и т. д.
На рис. 2.16 представлены функции R1(tk ,τ)										(2.32) для момен-
тов времени t k		= k.
	0.03
	0.029			1
	0.029			2
				2
	0.028			3
	0.027			4	5	6
						6
	0.026					7	8	9
	0.025					7	8	9
R	0.025
	0.024							10
	0.024
	0.023
	0.022
	0.021
	0.020	1	2	3	4	5	6	7	8	9	10
						τ [сут]					τ сут
	Рис. 2.16. Вид функции влияния R1								для бетона:
кривая 1 соответствует функции R1(t1,τ); кривая 2 – R1(t2,τ) и т. д.
						56

Глава 2. Математические модели деформирования элементов строительных...

Для стержня физические соотношения с учетом ползучести

материала принимают вид
σx(t) = σУx (t)−σСx (t),			(2.33)
где σУ имеет вид (2.13), а	σс	записывается в виде
x	x
		t
σСx (t) = E∫εxz (τ)R1(t,τ)dτ.			(2.34)

Для пластин, работающих на изгиб, и оболочек при учете ползучести материала на основе линейной теории наследственности физические соотношения можно представить едиными формулами

σx(t) = σУx (t)−σСx (t), σy(t) = σУy (t)−σСy (t);

τxy(t) = τУxy(t)−τсxy(t),

(2.35)

гделинейно-упругиесоставляющиенапряжений σУx (t), σУy (t), τУxy(t)

заданы соотношениями (2.14)для пластин и (2.15)для оболочек; составляющие, характеризующие ползучесть материала, имеют вид

(t)

τ;

τ +µε

−µ

2 ∫[

x( )

( )]R1

(t, )d

σСy

(t) =

∫t [εzy (τ)+µεxz

(τ)]R1(t,τ)dτ;

1−µ

τСx (t) =

∫γxyz

(τ)R2(t,τ)dτ.

(2.36)

2(1+µ)

Деформации εzx , εzy , γzxy, входящие в соотношения (2.36), зада-

ны формулами (2.8), (2.9) для плит и соотношениями (2.10), (2.11) – для оболочек.

2.7. Принцип возможных перемещений. Полная энергия деформации

Конструкцииприходитсявосновномрассчитыватьнадействие внешних сил. В статических расчетах предполагают, что внешние силы прикладываются постепенно, без заметных скоростей и уско-

Математическое моделирование и расчет элементов строительных конструкций

рений, что дает основание пренебречь силами сопротивления среды и силами инерции.

Прирасчетеконструкцийлюбойсложностичащевсегоиспользуются приближенные методы решения уравнений равновесия, вывод которых основан на вариационных принципах. Пусть на некото-

рую конструкцию действуют объемные силы X (X1,X2 ,X3) и поверхностные нагрузки Pv (Pv1,Pv2 ,Pv3 ) на некоторой части поверхности S1.

На		оставшейся								части поверхности заданы перемещения
u	S	=	u	(	u1,	u	2 ,	u	3 )	. Под действием приложенных нагрузок конструк-

		2

ция получает перемещения u(u1, u2 , u3 ), в результате чего возника-

ютдеформации εij инапряжения σij .Далее,пустьперемещениятела в его равновесном состоянии получили возможные перемещения δu1,δu2 ,δu3, что привело к появлению бесконечно малых деформа-

ций δεij и напряжений δσij . Согласно принципу возможных переме-

щений если конструкция находится в равновесии, то сумма работ внешних и внутренних сил на любых возможных бесконечно малых перемещениях, не противоречащих кинематическим связям, равна нулю. То есть

∫∫∫σij δεij dV − ∫∫∫ Xi δuidV − ∫∫Pvi δuidS = 0 .			(2.37)
V	V	S1
Принцип возможных перемещений в данной формулировке

(2.37)справедливпри любыхсвойствахматериалатела [14], т. е. при произвольном законе связи между компонентами напряжений и деформаций и произвольном законе кинематической связи между ком-

понентами перемещений ui и деформаций εij .

Полная энергия деформации тела представляет собой функци-

онал (2.3).

При линейно-упругом деформировании полная энергия деформации для стержня будет иметь вид:

	1	l	h / 2	l
Э =	1	∫	∫σxεxz	dxdz − ∫q(x)wdx;	(2.38)
	2	0 −h / 2		0
		0 −h / 2		0

Глава 2. Математические модели деформирования элементов строительных...

для пластины и оболочки:

1 a b

h /2

xy ]dxdydz

a b

∫∫ ∫[

+ ε

+ γ

−

∫∫q(x, y)wdxdy.

(2.39)

0 0

−h / 2

0 0

Рассматривая потенциальную энергию П как функцию компонент деформации и учитывая зависимости между напряжениями идеформациями(2.13),(2.14),найдемвариациюфункционалов(2.38), (2.39).

Для стержня получим

h /2

δЭ =

∫

(σx δεxz

+εxz δσx

)dxdz − ∫qδw dx =

0 −h /2

= 1

∫l

h∫/2(Eεxz δεxz

+εxz δ(Eεxz ) )dxdz −∫l qδw dx =

0 −h /2

h /2

= ∫

∫σxδεxz dxdz −∫qδw dx .

(2.40)

0 −h /2

Для пластины и оболочки имеем

1 a b

h /2

δЭ =

∫∫ ∫(σx δεxz

+εxz δσx +σy δεzy +εzy δσy +

0 0 −h /2

a b

+ τxy δγxz + γxyz

δτxy )dxdydz −∫∫qδwdxdy =

0 0

a b h/2

∫∫ ∫

−µ

2 [εx

+µεy

]δεx

+εx

−µ

δ[εx

+µεy ]+

0 0 −h /2

[εzy +µεxz ]δεzy

+εxz

δ[εzy +µεxz ]+

1−µ2

a b

γxyδγxy + γxy

δγxy

dV −∫∫q δw dxdy =

2(1+µ)

0 0

a b

h /2

a b

= ∫∫

∫(σx δεxz

+ σy δεzy + τxy δγxz )dxdydz − ∫∫q δw dxdy. (2.41)

0 0 −h /2

0 0

<<< < Предыдущая 1 23 / 93 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.08.2019175.5 Кб3Karin Kallmaker - Making Up for Lost Time.docx
#
28.08.2019288.12 Кб1Karin Kallmaker - Once Upon a Dyke.docx
#
28.08.2019205.06 Кб2Karin Kallmaker - Paperback Romance.docx
#
28.08.2019226.76 Кб3Karin Kallmaker - Unforgettable.docx
#
28.08.2019283.48 Кб4Karin Kallmaker - Warming Trend.docx
#
12.03.20162.37 Mб336Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013.pdf
#
07.09.2019259.68 Кб2Kate Sweeney - Sea of Grass.docx
#
07.09.2019430.08 Кб1Katherine V. Forrest - Curious Wine.doc
#
07.09.2019288.5 Кб1Kathy Higgs - Yvonne 1 - Before You.docx
#
07.09.2019637.38 Кб1KG MacGregor - Anna and Lily Stories.docx
#
07.09.2019185.7 Кб3KG MacGregor - Just This Once.docx