Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013

.pdf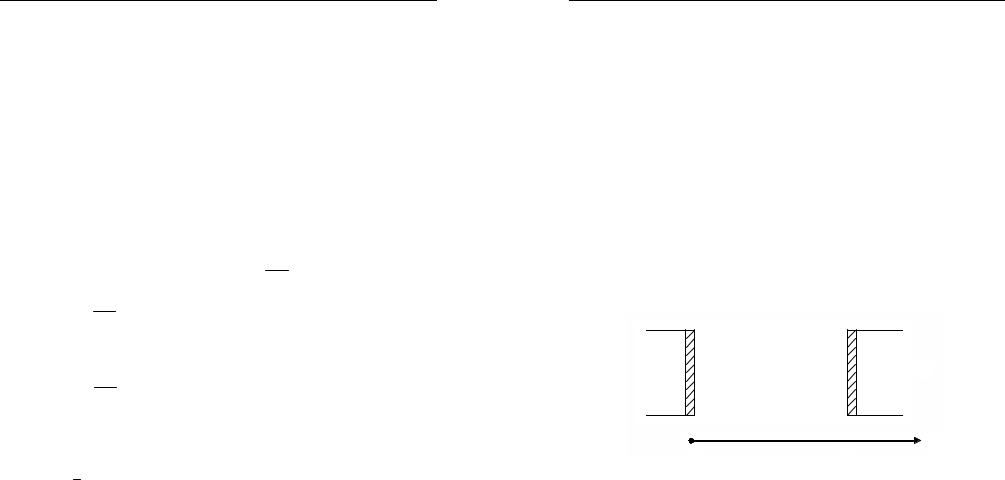

Скачиваний:

336

Добавлен:

12.03.2016

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Математическое моделирование и расчет элементов строительных конструкций

Уравнения (1.12), (1.19) содержат пять неизвестных величин – ρ,P,vx ,vy ,vz . Недостающее уравнение получим из уравнения энергии, используя закон сохранения энергии. Будем рассматривать изменение внутренней энергии фиксированной массы газа dm за ко-

роткий промежуток времени dt . Так как по сделанным допущениям ввеществеотсутствуеттеплопроводность,вязкостьиисточники(стоки) энергии, то это изменение вызывается лишь работой сил давления на гранях кубика при его сжатии или растяжении.

Работа давления, связанная с движением грани объема вдоль оси x , очевидно, равна

dAx = P[vx (x)−vx (x +dx)]dtdydz ,

где слагаемые в скобках можно, отбрасывая члены второго порядка

малости, переписать через производную ∂vx и получить

∂x

dAx = −P ∂∂vxx dxdydzdt.

Здесь P – среднее давление в элементарном объеме. Аналогично,

dAy = −P ∂∂vyy dxdydzdt;

dAz = −P ∂∂vzz dxdydzdt.

Полная работа, совершаемая над газом за время dt , будет

dA = −Pdiv v dxdydzdt .

Она равна изменению внутренней энергии объема, т. е. dA = ρdεdxdydz , где ε – удельная внутренняя энергия.

Приравняв оба выражения для dA и устремив к нулю dt , окончательно получим

ρdε	+ Pdivv = 0 ,	(1.20)
dt

dε

где dt – полная (субстанционная) производная внутренней энергии по времени.

Глава 1. Основы математического моделирования

С помощью уравнения неразрывности (1.12) и движения (1.18) уравнение (1.20) приводится к дивергентному виду

∂

ρv

ρε+

ε+

+ Pv .

(1.21)

∂t

= −div ρv

Слева в (1.21) стоит производная от полной (внутренней и кинетической) энергии газа в данной точке пространства.

Так как термодинамические свойства вещества предполагаются

известными, то ε –известная функция уже введенныхвеличин P и ρ. Таким образом, для определения пяти неизвестных –

ρ,P,vx ,vy ,vz получили пять уравнений (1.12), (1.19), (1.21). Для их

решения необходимо задать еще начальные и краевые условия. Наиболее наглядна постановка этих условий в случае одномер-

ного течения газа. Рассмотрим такое течение в трубе, внутри которой помещен газ, ограниченный справа и слева непроницаемыми твердыми стенками-поршнями (рис. 1.6).

	v0 (m), ρ0 (m),	P(M ,t)
v(0,t)	P0 (m)	P(M ,t)

0	M	m
Рис. 1.6. Течение газа внутри трубы

Частицам, находящимся улевой стенки, припишем координату m = 0 ; тогда координата частиц у правой стенки равна m = M , гдеM – полная масса газа между поршнями в столбце единичного сечения. Внутренние частицыимеюткоординату 0 < m < M . Дляопределения течения при всех 0 < m < M и t > 0 необходимо задать:

1) начальные условия, т. е. состояние газа в момент t = 0:

v(m,0) = v0 (m), P(m,0) = P0 (m), ρ(m,0) = ρ0 (m),	(1.22)
0 < m < M ;

Математическое моделирование и расчет элементов строительных конструкций

2) граничные условия, т. е. зависимость от времени газодинамических величин на гранях m = 0, m = M , например закон изменения давления

P(0,t) = P1(t), P(M ,t) = P2 (t), t > 0 ,

(1.23)

или закон изменения скорости поршней (т. е. их траекторию)

v(0,t) = v1(t), v(M ,t) = v2 (t), t > 0 .

Могут быть и другие граничные условия.

Таким образом, найденные уравнения вместе с начальными и краевыми условиями определяют математическуюмодель, описывающую течение сжимаемого газа.

1.5. Построение математических моделей на основе применения вариационных принципов

Суть построения математических моделей на основе вариационных принципов состоит в построении функционала полной энергии изменения (например деформации, для механических систем) изучаемогопроцессаиминимизацииэтогофункционала,т.е.нахождения уравнений Эйлера для этого функционала.

Рассмотрим этот прием на примере вывода уравнений равновесия пластины толщиной h , находящейся под действием поперечной нагрузки q(x,y) (рис. 1.7).

x	y
a	b

Рис. 1.7. Пластина постоянной толщины

Срединную поверхность (плоскость) пластины примем за координатную и сведем трехмернуюзадачук двумерной относительно деформациисрединнойповерхности,введяследующиеограничения:

Глава 1. Основы математического моделирования

1.Пластина допускает малые прогибы, поэтому соотношения междудеформациямииперемещениями(геометрическиесоотношения) будут линейными.

2.Справедлива гипотеза прямой нормали, согласно которой первоначально прямолинейный и нормальный к срединной поверхностиэлементостаетсяпридеформированиипластиныпрямолинейным и нормальным. При этом перемещения в слое, отстоящем на z от срединной поверхности, имеют вид

U z =U − z	∂W	, V z =V − z	∂W	, W z =W ,
	∂x		∂y

где U,V ,W – перемещения точек срединной поверхности вдоль ко-

ординат x,y,z .
h	<	1
3. Для тонких пластин			пренебрегаем вертикальными
3. Для тонких пластин		20	пренебрегаем вертикальными
a		20

напряжениями σz = 0 .

4.Будемсчитать,чтовпластинеподдействиемнагрузкивозникают только изгибные деформации.

5.Материал пластины изотропный и упругий (связь между напряжениями и деформациями линейная). Основные соотношения деформированияпластинысостоятизгеометрическихифизических соотношений и функционала полной энергии деформации.

При введенных предположениях геометрические соотношения

всрединной поверхности будут иметь вид (связь между деформациями и перемещениями)

εx =

∂U

, εy =

∂V

γxy

∂U

∂V

;

(1.24)

∂x

∂y

∂x

в плоскости, отстоящей на z

от срединной поверхности,

εxz = εx

− z ∂2W ,

εzy = εy − z

∂2W

, γxyz = γxy −2z

∂2W .

∂x2

∂y2

∂x∂y

ФизическиесоотношениясогласнозаконуГукапринимаютвид

σx =

(εxz

+µεzy ), σy

(εzy +µεxz ),

(1.25)

1−µ

τxy

γxyz ,

2(1+µ)

Математическое моделирование и расчет элементов строительных конструкций

а с учетом ограничения 4 (учитываются только изгибные деформации)

∂

∂2W

= −

+µ

= −

+µ

−µ

∂x

∂y

−µ

∂y

∂x

τxy = −

∂2W .

(1+µ) ∂x∂y

Функционал полной энергии деформации пластины с учетом

предположения 2 и 4 принимает вид:

1 a b

∂2W

= −

2 + M y

2 + 2M xy

∫∫ M x

∂x

∂y

∂x∂y

+ 2qW dxdy . (1.26)

0 0

Здесь

Eh3

∂2W

M x = ∫zσxdz

= −

2 +µ

;

12(1

−µ

)

∂x

∂y

−

Eh3

∂2W

M y = ∫zσydz

= −

2 +µ

;

12(1

−µ

)

∂y

∂x

(1.27)

−

Eh3

∂2W .

M xy = ∫2 zτxydz = −

−h2

12(1+µ) ∂x∂y

НаосновевариационногопринципаЛагранжа(принципавозмож-

ных перемещений) первая вариация функционала (1.26) равна нулю

a b			2		2
δЭ = −∫∫	M xδ		∂ W2	+ M yδ	∂ W2 +
0 0			∂x		∂y
	∂2W
+2M xyδ						(1.28)
+2M xyδ	∂x∂y	+ qδW dxdy = 0.				(1.28)
	∂x∂y

Теперь вариационное уравнение δЭ = 0 нужно преобразовать так, чтобы под знаком двойного интеграла не было вариаций от про-

Глава 1. Основы математического моделирования

изводных искомой функции прогиба W (x,y). Применяя интегрирование по частям, вариационное уравнение приведем к виду:

a b

M x

∂

M y

∂

M xy

− ∫∫

∂

∂x

∂y

+ 2

∂x∂y

δWdxdy +

0 0

∂M

∂M xy

∂W

x=a

∫

δW − M xδ

dy +

∂x

∂y

∂x

x=0

∂M

δ∂W

y=b

x=a

y=b

(1.29)

∫

δW −M

dx −2M

= 0.

∂y

∂x

∂y

y=0

x=0

y=0

Суть преобразований вариационного уравнения (1.28) заключается в следующем

a b

∂2W

a b

∂M

∂W

x=a

∂W

dxdy =

∫∫M xδ

∂x

dxdy = ∫M xδ

∂x

x=0

dy − ∫∫

∂x

0 0

∂W

x=a

b ∂M

x=a

a b

∂2M

= ∫M xδ

dy −∫

x δW

dy + ∫∫

δWdxdy;

∂x

x=0

∂x

0 0

a b

∂2W

a b

∂M y

∂W

y=b

∂W

∫∫M yδ

dxdy = ∫M yδ

∂y

dx −∫∫

dxdy =

∂y

y=0

∂y

0 0

∂W

y =b

a ∂M y

y=b

a b

∂2M y

= ∫M yδ

dy − ∫

δW

dx + ∫∫

δWdxdy;

∂y

y =0

∂y

y=0

∂y

0 0

a b

∂2W

a b

∂M xy

∂W

x=a

∂W

∫∫M xyδ

∂x∂y

dxdy = ∫M xy

∂y

dy − ∫∫

dxdy =

x=0

∂x

∂y

0 0

x=a

y=b

∂M xy

x=a

= M xyδW

−

∫0

δW

dy −

x=0

y=0

∂y

x=0

∂M xy

y=b

a b

∂2M xy

− ∫

δW

dx +∫∫

δWdxdy;

∂x

y=0

∂x∂y

0 0

Математическое моделирование и расчет элементов строительных конструкций

a b	∂2W	a			a b	∂M xy
			∂W	y=b				∂W
∫∫M xyδ		dxdy = ∫M xyδ			dx − ∫∫		δ		dxdy =
	∂x∂y		∂x	y=0		∂y		∂x
0 0		0			0 0

x=a

y=b

∂M xy

y=b

= M xyδW

−

∫0

δW

dx −

∂x

x=0

y=0

∂M xy

x=a

a b

∂2 M xy

− ∫

δW

dy +∫∫

δWdxdy.

∂y

x=0

∂x∂y

0 0

Из вариационного уравнения (1.29) на основе основной леммы

вариационного исчисления получаем уравнение равновесия

∂2M

∂2M y

∂2M xy

+q = 0

(1.30)

∂x2

∂y2

∂x∂y

и краевые условия на контуре пластины:

при x = 0,

x = a

∂M

x +2

∂M xy

= 0

или W = 0 ;

(1.31)

∂x

∂y

M x

= 0 или

∂W

= 0;

∂x

при y = 0,

y =b

∂M y

∂M xy

= 0 или W = 0 ;

(1.32)

∂y

∂x

M y = 0 или ∂∂Wy = 0.

Если в уравнение (1.30) подставить выражение моментов через прогиб W (1.27), то получим уравнение

∂4W

∂4W ∂4W

= q ,

∂x

∂y

2 +

∂y

(1.33)

где D =

Eh3

12(1

−µ2 )

Глава 1. Основы математического моделирования

Таким образом, моделью деформирования пластины малого прогиба, при условии, что она испытывает только изгибные деформации, будет дифференциальное уравнение (1.33) с соответствующими краевыми условиями, которые выводятся из (1.31), (1.32).

Например, если пластина по краю жестко закреплена, то

W = 0 , ∂∂Wx = 0 при x = 0, x = a ;

W = 0 , ∂∂Wy = 0 при y = 0, y = b .

1.6. Построение математической модели механических систем на основе приравнивания нулю суммы проекций силовых факторов по осям координат

Получимматематическуюмодельдеформирования трехмерноготела,находящегосяподдействиемобъемныхиповерхностныхсил.

Обозначим проекции объемной силы, приходящейся на единицуобъема тела, через X ,Y,Z, а составляющие поверхностной силы,

отнесенной к единице площади тела, через X ,Y ,Z .

Рассмотримравновесиеэлементарногопараллелепипеда,вырезанного из тела, находящегося в напряженном состоянии под действием внешних нагрузок (рис. 1.8).

Размеры ребер параллелепипеда dx,dy,dz . Учитывая допуще-

ние о сплошности и однородности материала, можно полагать, что и напряжения внутри тела от одной точки к другой будут изменяться непрерывно. Если на гранях параллелепипеда, совпадающих

скоординатными плоскостями, будут действовать напряжения

σx ,σy ,σz ,τxy ,τxz ,τyz , то на грани, отстоящей на расстоянии dx от

координатной плоскости z0 y , будут действовать напряжения

σx + ∂∂σxx dx, τyx + ∂τ∂xyx dx, τzx + ∂τ∂xzx dx,

на грани, отстоящей на расстоянии dy от координатной плоскости z0x , напряжения

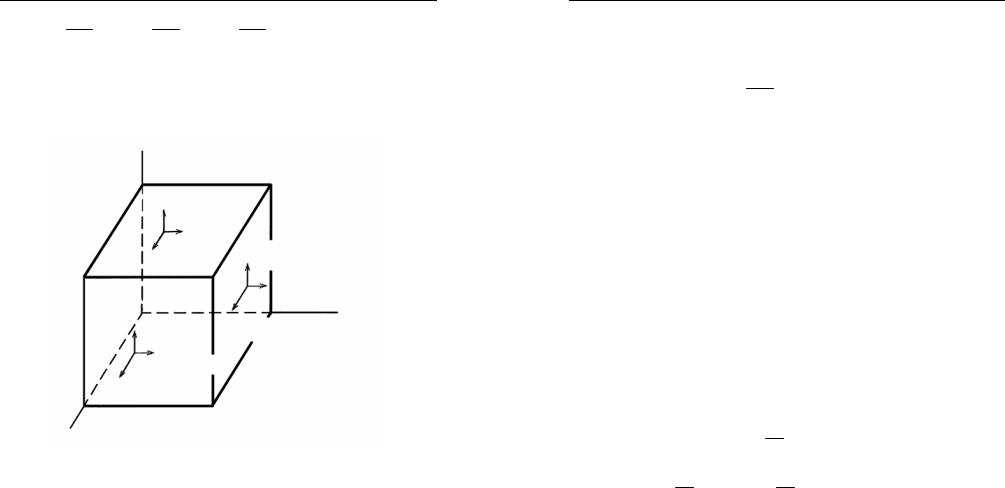
Математическое моделирование и расчет элементов строительных конструкций

σy + ∂σ∂yy dy, τxy + ∂τ∂yxy dy, τzy + ∂τ∂yzy dy

и, наконец, на грани, отстоящей на расстоянии dz от координатной плоскости x0y , напряжения будут

σ z

∂σ z

dz ,

τ xz +

∂τ xz

dz ,

τ yz

∂τ yz

dz .

∂z

σz

∂σz

∂z

∂τyz

τyz

∂z

∂τzy

∂τxz

τxz +

∂y

∂z

∂σy

σy +

∂y

∂τxy

∂τ

τzx +

dx τxy +

∂y

∂x∂τyx

τyx +

∂x

σx

∂σx

∂x

Рис. 1.8. Равновесие элементарного параллелепипеда, находящегося в напряженном состоянии

Для твердого тела можно записать шесть уравнений равновесия: три уравнения – условия равновесия сил, действующих в направлении трех осей координат 0x, 0y, 0z, и три условия равновесия моментов относительно этих осей.

Проектируя все силы на ось 0x, будем иметь

∂σ

∂τxy

∂τ

σx +

dx dydz +

τxy +

dy dxdz + τxz +

dz dxdy −

∂x

∂y

∂z

−σxdydz −τxydxdz −τxz dxdy + Xdxdydz = 0 .

Глава 1. Основы математического моделирования

Аналогично можно получить сумму проекций всех сил на оси 0y и 0z. После сокращения на общий множитель получим следующую систему дифференциальных уравнений равновесия:

∂∂σxx + ∂τ∂yxy + ∂∂τzxz + X = 0 ;


∂τyx		+	∂σy	+		∂τyz		+Y = 0	;
			∂y
∂x						∂z
∂τ	zx +		∂τzy		+	∂σ	z + Z = 0		.	(1.34)
			∂y
∂x						∂z

Условия равновесия моментов относительно 0x, 0y, 0z для выделенного элементарного параллелепипеда приводят к соотношени-

ям τxy = τyx ,τxz = τzx ,τyz = τzy – закону парности касательных напряжений. Поэтомув уравнениях (1.34)не девять, а шесть независимых составляющих, характеризующих напряженное состояние вточкетела.Условияравновесиядаюттридифференциальныхуравнения для определения шести неизвестных составляющих напряжений как функций координат точки.

Можно напряжения выразить через перемещения u,v,w и тогда относительно перемещений будет достаточно уравнений.

Связь между деформациями и перемещениями имеет вид

ε x = ∂∂ux , ε y = ∂∂yv , ε z = ∂∂wz , γ xy = ∂∂uy + ∂∂vx , γ xz = ∂∂uz + ∂∂wx , γ yz = ∂∂vz + ∂∂wy ,

асвязь междунапряжениями и деформациямидляизотропного тела –

σx = 2Gεx +λ∆, τxy = Gγxy ,

σy = 2Gεy +λ∆, τyz = Gγyz ,

σz = 2Gεz +λ∆, τzx = Gγzx ,

где G =	E	; ∆ = εx + εy + εz ; λ =	2µG	; E, µ – модуль упруго-
	2(1+µ)		1− 2µ

сти и коэффициент Пуассона материала тела.

Математическое моделирование и расчет элементов строительных конструкций

К уравнениям равновесия (1.34) необходимо добавить краевые условия,которыевыражаютусловияравновесиянаповерхноститела,

ипринимают вид

σx l + τ xy m + τ xz n − X = 0,

τ yx l +σ y m + τ yz n −Y = 0,

τ zx l + τ zy m + σ z n − Z = 0,

где l ,m ,n – направляющие косинусы нормали, проведенной к площадке поверхности тела.

1.7. Математические модели, получаемые при экспериментальном исследовании процесса

Во многих областях науки и техники исследование того или иного явления или процесса возможно только эмпирически, т. е. с помощью опыта или эксперимента.

Результатом эксперимента является получение числовых значений выходного параметра y в зависимости от конкретных значе-

ний входных параметров (факторов) x1,x2 ,...,xk . При этом изначаль-

но внутренняя структура функционирования процесса неизвестна. Входные и выходные параметры по своей природе величины случайные. Следовательно, при обработке экспериментальных дан-

ных нужно пользоваться методами математической статистики.

В результате проведения эксперимента возникают следующие основные задачи:

1.Первичная статистическая обработка результатов эксперимента. Для этого определяются среднее значение выходного параметра при многократном повторении одного и того же набора входных параметров и разброс вокруг этого среднего значения, т. е. дисперсия и среднеквадратическое отклонение.

2.Обоснованиеточностиполученныхэкспериментальныхданных, в том числе средних значений выходного параметра и среднеквадратичных отклонений, а также числа повторений наборов входных параметров. Для этого используется доверительный интервал

икритерии согласия.

Глава 1. Основы математического моделирования

3. Определение аналитической зависимости выходного параметра y от входных параметров x1,x2 ,...,xk

y = f (x1,x2 ,...,xk ),

т. е. математической модели изучаемого процесса. Эта аналитическаязависимостьназываетсяфункциейотклика.Дляэтогоможетбыть применен метод наименьших квадратов.

4. Планирование эксперимента, т. е. выбор наилучшего эксперимента с позиций затрат материальных ресурсов и точности описания процесса.

Кроме того, может оказаться, что некоторые входные параметры мало влияют на выходной параметр и их можно исключить из

рассмотрения. Выяснить, зависимы ли случайные величины y и xi ,

можно если определить коорреляционную зависимость между этимислучайнымивеличинамии оценить, например, коэффициенткор-

реляции между величинами y и xi .

Итак, врезультате проведенияэксперимента получена табл. 1.1 значений y в зависимости от значения входного параметра x (пусть будет один входной параметр).

							Таблица 1.1
	Зависимость y от xi ,полученная вэксперименте
	x	x1		x2		…	xm
	y	y1		y2		…	ym
Считается, что проведена первичная статистическая обработка
результатов эксперимента,					т. е. каждое значение xi		входного пара-
метра x повторялось n				раз и получены значения yi1,yi2 ,...,yin .
			i					i

			n
			∑i	yik
За yi	взято значение yi	=	k=1		.
За yi	взято значение yi	=			.
			ni

Кроме того, найдено среднеквадратическое отклонение σi . Теперь необходимо оценить найденные значения yi и σi , используя, например, критерии согласия.

Математическое моделирование и расчет элементов строительных конструкций

Чтобы найти аналитическую зависимость y = f (x), применяется метод наименьших квадратов. Функция y = f (x) должна отражать в основном характер экспериментальной зависимости (это не интерполяционный многочлен). Эту функцию называют еще сглаживающей. Возьмем функцию y = f (x) в виде линейной комбина-

ции неизвестных числовых параметров ci	и некоторых линейно-не-
зависимых функций ϕi (x)
n
y = ∑ciϕi (x).	(1.35)

i=1

Вкачестве функций ϕi (x) могут быть степенные функции xi . Исходя из метода наименьших квадратов, неизвестные число-

вые параметры ci находятся из условия, чтобы сумма квадратов от-

клонений опытных значений функции y от значений сглаживающей функции (1.35) при одинаковом значении x была бы минимальной:

S =

−

∑

)

→ min.

∑

k=1

i=1

Функция S является функцией n параметров c1,c2 , ,cn . Не-

обходимые условия экстремума функции S имеют вид

∂S

= 0 (j =1,2, ,n).

∂c j

В результате получим

∂S

= −2

−

∑

) ϕ

) = 0

(1.36)

∂сj

∑

k=1

i=1

Получили для определения ci систему линейных алгебраичес-

ких уравнений, которая может быть решена методом Гаусса. Можетоказаться,чтодлянайденныхзначенийслучайнойвели-

чины y необходимо определить закон распределения вероятностей. Если заранее известно, что случайная величина y распределена по нормальному закону, то, найдя (см. табл. 1.1)

∑yk

M[y]= a = k=m1

Глава 1. Основы математического моделирования

и σ, можно записать закон распределения вероятностей случайной величины y в виде

f (y) = σ 12π e−(y2−σa2)2 .

Используякритериисогласия,можнопроверитьсправедливость гипотезы о том, что случайная величина y распределена по нормальному закону.

1.8. Математические модели задач оптимизации

Экономическое планирование, управление, распределение ограниченных ресурсов, анализ производственных процессов, проектирование сложных объектов всегда должны быть направлены на поиск наилучшего варианта с точки зрения намеченной цели, т. е. приводят к задачам оптимизации.

Впервые (в 1930 году) математическая постановка таких задач была осуществлена российским экономистом А. Н. Толстым в виде предложения по составлению такого плана перевозок грузов между пунктами, чтобы общий пробег транспорта был наименьшим.

Рассмотримнекоторыезадачивыборанаилучшегорешения(оптимизации) и перейдем от содержательной постановки задачи к математической формализации (математической модели).

Задача 1 (транспортная задача)

В городе имеется 2 бетонных завода. Первый выпускает в день 400 т бетона, а второй – 560 т. Бетон с этих заводов отправляется на 4 стройплощадки. На первуюстройплощадку поступает в день 220 т бетона, на вторую – 200 т, на третью – 180 т, на четвертую – 360 т. Стоимость перевозки одной тонны бетона с каждого завода на каждую стройплощадку известна. Требуется так организовать перевозку бетона с заводов на стройплощадки, чтобы суммарная стоимость всех перевозок была минимальной.

От содержательной постановки задачи перейдем к математической. Если через сij обозначить стоимость перевозки одной тонны бетона с i -го завода на j -ю стройплощадку (это известные величи-

Математическое моделирование и расчет элементов строительных конструкций

ны), а через xij – количество тонн бетона, которое нужно перевезти с i -го завода на j-ю стройплощадку (это искомые величины), то стоимость всех перевозок будет выражаться функцией

	2	4
f	= ∑∑cij xij .		(1.37)
	i=1 j=1

Необходимо найти минимум этой функции, но xij не независи-

мы, они связаны между собой следующими ограничениями. С первого завода вывозится 400 т бетона, следовательно,

∑x1 j = 400.

j=1

Со второго завода выводится 560 т бетона, следовательно,

∑x2 j = 560.

j=1

Напервуюстройплощадкузавозится220 тбетона, следовательно,

∑xi1 = 220.

i=1

Аналогично можно записать для остальных стройплощадок

2	2		2
∑xi2	= 200, ∑xi3	=180,	∑xi4	= 360.
i=1	i=1		i=1

Таким образом xij должны удовлетворять следующей системе ограничений:

4	4		2
∑x1 j = 400	,∑x2 j = 560	,∑xi1		=	220,
j=1	j=1		i=1
2	2		2
∑x i 2 = 200 ,	∑x i 3 =180,		∑x i 4		= 360.	(1.38)
i=1	i=1		i=1

К этим ограничениямнеобходимо добавить еще xij ≥ 0 (так как

обратно бетон со стройплощадок на заводы не увозится). Математически задача ставится так: найти минимум функции

(1.37) при условии, что ее аргументы удовлетворяют системе урав-

нений (1.38).

Глава 1. Основы математического моделирования

Задача 2

Найти оптимальнуюмассу плоской фермы привыполнении условий прочности (рис. 1.9).

		F
1	B	2
	B

Рис. 1.9. Статически неопределимая стержневая система: 1–4 – стержни

Статическинеопределимаяшарнирно-стержневаясистема(фер- ма) нагружена силой F .

Необходимо выбрать площади поперечных сечений Ai	таким
образом, чтобы общая масса M фермы была минимальной:
Длина стержней l, м, известна:
l1 = 6,3246; l2 = 6,03; l3 =12; l4 = 2,6; BC = 2; CD = 0,6.
Масса фермы определяется формулой
M = ρ(12,6492A1 +12,06A2 +12A3 +2,6A4 ),	(1.39)
где ρ – удельный вес материала стержней.

Выражение (1.39) – функция цели, минимум которой нужно найти.

Систему ограничений составим из условий прочности. Требуется, чтобы во всех стержнях фермы напряжения не превосходили по абсолютной величине расчетного сопротивления материала стер-

жней R (одинакового на растяжение и сжатие), т. е.	N	≤ R.
жней R (одинакового на растяжение и сжатие), т. е.	Ai	≤ R.
	i
Следовательно,системаограниченийпредставляетсяввидедвух
неравенств:
Ni + RAi ≥ 0 , − Ni + RAi ≥ 0,	(1.40)
где Ni – усилия в стержнях фермы.
35

Математическое моделирование и расчет элементов строительных конструкций

Первое неравенство (1.40) означает, что стержень работает на сжатие,второе–нарастяжение.Таккакстержни1 и4 работаюттолько на сжатие, 2 – только на растяжение, то систему (1.40) можно записать в виде

N1 + RA1 ≥ 0; N4 + RA4 ≥ 0; − N2 + RA2 ≥ 0;
N3 + RA3 ≥ 0; − N3 + RA3 ≥ 0.	(1.41)

Исходяизусловийравновесиявузлахфермы,получимтриуравнения с четырьмя неизвестными:

N1 = −1,5812N4 −1,5812F ; N2 = −5,025N4 ; N3 = 6,5N4 +1,5F .

Подставляя эти выражения в неравенства (1.41) и вводя дополнительные переменные yi , получим системуограничений в виде равенств:

y1 − RA1 +1,5812N4 = −1,5812F ; y2 − RA2 −5,025N4 = 0;

y3 − RA3 −6,5N4 =1,5F ; y4 − RA3 +6,5N4 = −1,5F ;

y5 − RA4 − N4 = 0.

(1.42)

Таким образом, математически задача ставится так: найти минимум функции (1.39) при условии, что ее аргументы удовлетворяют системе уравнений (1.42).

Такого типа задачи оптимизации относятся к математической дисциплине, названной математическим программированием (заметим, что термин «программирование» во время становления этой математической дисциплины еще не использовался для написания программ для ЭВМ, так как ЭВМ тогда еще не было).

Различают следующие виды математического программирования: линейное, нелинейное, динамическое и др.

В канонической форме задача линейного программирования ставитсятак: найти глобальный минимумлинейной функцииn аргу-

ментов (функции цели) f = f0 +∑ci xi при условии, что аргументы

i=1

этой функции удовлетворяют следующей совместной неопределенной системе линейных алгебраических уравнений

Глава 1. Основы математического моделирования

a11x1 + a12 x2 + + a1n xn = b1 , a21x1 +a22 x2 + +a2n xn = b2 ,

am1x1 + am2 x2 + +amn xn = bm .

1.9. Исследование адекватности математической модели изучаемому объекту

Таккакдля одногоитогоже объекта или явленияможносоставить несколько математических моделей, то важной задачей становится выбор такой модели, которая была бы наиболее простой и в то же время в рамках требуемой точности правильно отражала свойства изучаемого объекта.

Для анализа адекватности модели реальному процессу и выбора наиболее оптимальной модели проводят натурный эксперимент. Так поступают в различных областях техники, особенно при исследованииработы космическойиавиационной техники. Но можнодля этих целей провести и вычислительный эксперимент, сравнивая результаты исследования объекта на разных моделях.

Присоставлениифизическоймоделиобъектаилипроцессавводятся некоторые упрощения путем пренебрежения некоторыми факторами или характеристиками процесса, после чего уже происходит формирование математической модели.

Уже на этом этапе построения модели проводят анализ отбрасывания факторов и их влияния на точность математической модели, т. е. проводится некоторый анализ адекватности модели изучаемому процессу.

1.10. Иерархический подход к получению математических моделей. Уточнение математической модели

Лишь в редких случаях бывает удобным и оправданным построение математических моделей даже относительно простых объектов сразу во всей полноте, с учетом всех факторов, существенных дляегоповедения.Поэтомуестествененподход,реализующийпринцип «от простого к сложному», когда следующий шаг делается

Математическое моделирование и расчет элементов строительных конструкций

после достаточно подробного изучения не очень сложной модели. При этом возникает цепочка (иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве частного случая.

Построим такую иерархическую цепочку на примере расчета напряженно-деформированногосостояния(НДС)пластины, находя-

щейся под действием поперечной нагрузки q(x,y). В 1.5 построена

простейшая модель деформирования пластины малого прогиба (нагрузка невелика), когда пренебрегают погонными усилиями

(Nx = N y = Nxy = 0). При произвольной поперечной нагрузке и про-

извольном закреплении края оболочки нельзя пренебрегать погонными усилиями, поэтому математическая модель деформирования пластины изменится, если считать несправедливым ограничение 4) в 1.5. В этом случае получим уточненную модель деформирования пластины. Ограничения 1), 2), 3), 5) считаются справедливыми.

ВэтомслучаевариационноеуравнениеδЭ = 0 записывается в виде

a b						2
δЭ = ∫∫ N xδεx			+N yδεy +N xyδγxy − M xδ			∂ W2 −
0 0						∂x
	∂2W			∂2W
− M yδ		2 −2M xyδ					(1.43)
− M yδ	∂y	2 −2M xyδ		∂x∂y	−qδW dxdy = 0.		(1.43)
	∂y			∂x∂y

Здесь εx ,εy ,γxy имеют следующий вид (1.26):

Nx = ∫2 σx dz =

(εx +µεy );

1−µ

−h

N y = ∫2 σy dz =

(εy +µεx );

1−µ

−h

Nxy = ∫2

τxydz =

γxy.

(1.44)

2(1+µ)

−h

Глава 1. Основы математического моделирования

После преобразования вариационного уравнения (1.43) таким образом, чтобы под знаком двойного интеграла не было вариаций от

производных искомых функций U (x,y),V (x,y),W (x,y), получим уравнение равновесия в усилиях и моментах:

∂N

∂Nxy

= 0;

∂N y

∂Nxy

= 0;

∂y

∂x

∂2M

∂2 M xy

∂2 M y

+q = 0.

(1.45)

∂x2

∂x∂y

∂y2

После подстановки в (1.45) усилий (1.44) и моментов в виде (1.27) с учетом (1.24) получим систему дифференциальных уравнений в частных производных восьмого порядка относительно функций перемещений U,V ,W .

Добавив к этой системе краевые условия, получим искомую математическую модель деформирования пластины.

Если же прогиб пластины W (x,y) соизмерим с ее толщиной h, то зависимость деформаций от перемещений будет нелинейной

εx =

∂U

1 ∂W

εy =

∂V

∂W

∂x

∂y

∂x

∂y

γxy

∂U

∂V

∂W ∂W .

(1.46)

∂x

∂y

∂x

∂y

Усилия и моменты по-прежнему будут иметь вид (1.27), (1.44). Суть преобразования вариационного уравнения (1.43) покажем

на примере преобразования первого члена:

a b

∂U

∂W

a b

∂U

∫∫

dxdy =

∫∫

dxdy +

∂x

0 0

a b

∂Nx δUdxdy +

+ ∫∫Nx

∂W

∂W dxdy = ∫NxδU

x=a dy −∫∫

0 0

∂x

x=0

0 0

∂x

∂W

x=a

a b

∂

∂W

+ ∫Nx

∂x

δW

dy −

∫∫

∂x

δWdxdy .

x=0

0 0

∂x

<<< < Предыдущая 12 / 92 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
28.08.2019175.5 Кб3Karin Kallmaker - Making Up for Lost Time.docx
#
28.08.2019288.12 Кб1Karin Kallmaker - Once Upon a Dyke.docx
#
28.08.2019205.06 Кб2Karin Kallmaker - Paperback Romance.docx
#
28.08.2019226.76 Кб3Karin Kallmaker - Unforgettable.docx
#
28.08.2019283.48 Кб4Karin Kallmaker - Warming Trend.docx
#
12.03.20162.37 Mб336Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013.pdf
#
07.09.2019259.68 Кб2Kate Sweeney - Sea of Grass.docx
#
07.09.2019430.08 Кб1Katherine V. Forrest - Curious Wine.doc
#
07.09.2019288.5 Кб1Kathy Higgs - Yvonne 1 - Before You.docx
#
07.09.2019637.38 Кб1KG MacGregor - Anna and Lily Stories.docx
#
07.09.2019185.7 Кб3KG MacGregor - Just This Once.docx