
Karpov_Panin_Matematicheskoe_modelirovanie_i_raschet_elementov_stroitelnykh_konstruktsiy2013
.pdf
Математическое моделирование и расчет элементов строительных конструкций
|
|
|
|
|
Таблица 4.2 |
||
|
Числовыезначения функции ξ(s) |
||||||
|
|
|
|
|
|
|
|
i |
|
ξi |
si |
s1i |
s2i |
||
0 |
|
0 |
0 |
0 |
0 |
|
|
1 |
|
0,2509 |
0,25 |
0,249 |
0,2461 |
|
|
2 |
|
0,534 |
0,5 |
0,517 |
0,4903 |
|
|
3 |
|
1,03 |
0,75 |
0,9086 |
0,739 |
|
|
4 |
|
2,25 |
1 |
0,9845 |
1,0016 |
|
|
Физические соотношения при нелинейно-упругом деформировании материала конструкции на основе деформационной теории пластичности запишутся так [11, 14]:
|
|
|
σ |
|
= |
|
|
|
E |
|
|
|
[εz |
+µεz |
−ω(ε |
)(εz |
+µε)z |
] |
|
|
|
|||||
|
|
|
|
1−µ2 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
х |
|
|
|
x |
|
y |
|
|
i |
x |
y |
; |
|
|
|
||||||
|
|
|
σ |
|
|
= |
|
|
|
E |
|
|
[εz |
+µεz |
−ω(ε |
)(εz |
+µε)z ] |
|
(4.33) |
|||||||
|
|
|
|
|
1−µ2 |
|
|
|
||||||||||||||||||
|
|
|
|
y |
|
|
|
|
y |
|
x |
|
i |
|
y |
x |
; |
|
||||||||
|
|
|
|
|
|
|
|
τxy = |
|
|
|
E |
(γxyz |
−ω(εi )γxyz ). |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2(1+µ) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Приучетефизическойнелинейностифункционалполнойэнергии |
||||||||||||||||||||||||||
деформаций оболочки принимает вид: |
|
|
|
|
|
|
|
|||||||||||||||||||
Э = Эу −Эп. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функционал |
Э |
у |
имеет вид (4.24), а функционал |
|
запишетсятак: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эп |
|
|
|
||||
Эп = |
|
|
|
E |
|
|
|
∫а ∫b {I1 (ε2x + 2µε x ε y +ε2y + µ1γ2xy ) + |
|
|
||||||||||||||||
|
2 (1 − µ |
2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
) 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
+ 2 I 2 (εx χ1 + µε x χ2 + ε y χ2 + µε y χ1 + 2µ1 γ xy χ12 ) + |
||||||||||||||||||||||||||
|
|
|
+ I3 (χ12 + 2µ1χ1χ2 +χ22 + 4µ1χ122 )}dxdy, |
|
|
(4.34) |
||||||||||||||||||||
h |
|
+H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь Ik = |
2∫ω(εi )zk −1dz, |
|
k =1, 2,3, |
где ω(εi ) = mεi2 , m = a1( |
E |
)2. |
||||||||||||||||||||
|
|
|||||||||||||||||||||||||
−h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rb |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
Интенсивность деформаций можно представить в виде:
|
2 |
|
|
, |
|
||
εi = |
|
b1 +b2 z +b3z2 |
(4.35) |
||||
|
|
||||||
3 |
|||||||
|
|
|
|
|
|||
где b1 = ε2x + ε2y +εxεy + 14 γ2xy ;
b2 = 2εxχ1 + 2εyχ2 + εxχ2 +εyχ1 + γxyχ12 ;
b3 = χ12 +χ22 +χ1χ2 +χ122 .
4.6. Теория прочности хрупких материалов
Разработанонесколькотеорийпрочности, относящихсяк хрупкимматериалам[6,8,14].Какизвестно,характернымобразцомхрупкого материала является бетон.
Одна из теорий прочности хрупких материалов связана с главными напряжениями σ1,σ2 ,σ3 , которые задаются на трех взаимно
перпендикулярныхплощадках, на которыхкасательные напряжения равны нулю.
При сложном напряженном состоянии в каждой точке оболочкиизвестно напряженно-деформированное состояние, т.е. известны
напряжения σх,σу,τху. Главные напряжения можно найти из уравнения [14]:
σ3 −(σх + σу)σ2 +(σхσу − τ2ху)σ = 0. |
(4.36) |
Касательными напряжениями τxz ,τyz пренебрегают, ввиду их малости для тонких оболочек. Главные напряжения располагают в порядке убывания σ1 > σ2 > σ3 , одно из которых будет равно нулю.
Построение так называемых предельных поверхностей прочности и разрушения требует проведения для бетона большого количества довольно сложных экспериментов. Поэтому на практике используются критерии прочности – упрощенные гипотезы наступления предела прочности или разрушения при сложном напряженном состоянии. Они позволяют определить условия наступления текучести или разрушения при сложном напряженном состоянии на осно-
120 |
121 |

Математическое моделирование и расчет элементов строительных конструкций
вании результатов испытания образцов при некоторых простейших напряженных состояниях (обычно – растяжении, сжатии, изгибе).
Любое сложное напряженное состояние σ1,σ2 ,σ3 приводится к эк-
вивалентному одноосному с напряжением σэкв.
Основываясь на анализе разных теорий прочности хрупких материалов, была выбрана наиболее подходящая для использования в программном комплексе расчета оболочек теория Кулона – Мора. В соответствии с ней условия прочности и условия разрушения для бетона (или критерии прочности и разрушения, соответственно) записываются в следующем виде [2]:
σ − Rbt σ |
3 |
≤ Rbt |
условие прочности, |
(4.37) |
||
1 |
Rb |
k |
||||
|
|
|
|
|||
σ − |
Rbt |
σ |
3 |
= R |
условие разрушения; |
(4.38) |
|
||||||
1 |
Rb |
bt |
||||
|
|
|
|
|
||
где σ1,σ3 − главныенапряжения(среднее главноенапряжение σ2 не учитывается, что составляет незначительный недостаток теории); Rb , Rbt – расчетные сопротивления бетона осевому сжатию и осевому растяжению, соответственно (призменные прочности); k – нор-
мативный коэффициент запаса прочности (k = 2...4).
В формулах (4.37), (4.38) используются номинальные напряжения (от «единых» нагрузок) и единый коэффициент запаса прочности. Целесообразно при расчетах конструкций подходить к выбору коэффициентов запаса прочности дифференцированно, как, например, в действующих нормах делается выбор коэффициентов надежности g. Так, если коэффициенты запаса прочности назначать для каждого вида нагрузок, можно получать расчетные напряжения
S 1 , S 2 , S 3 . Тогда условие прочности Кулона – Мора приобретает более универсальный вид [2, 28]:
S − |
Rbt |
S |
3 |
≤ m R |
(4.39) |
|
|||||
1 |
Rb |
bt , |
|||
|
|
|
|
||
где m – «коэффициент однородности», учитывающий естественный разброс прочности от среднего значения.
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
4.7. Приведенный модуль упругости железобетона
Бетон – хрупкий материал, по-разному сопротивляющийся сжатию и растяжению (причем это различие велико: прочность на сжатие в 10–30 раз превосходит прочность на растяжение). В железобетонныхконструкцияхбетонпреимущественноиспользуетсядля восприятия сжимающих напряжений. Поэтому за основную характеристику (эталон) прочностных свойств бетона принята его проч-
ность на осевое сжатие. Временное сопротивление сжатию σu эта-
лонных кубов принимают за кубиковую прочность бетона. Классами по какому-либо признаку называют среднестатичес-
кие значенияосновныхконтрольныххарактеристик бетона, задаваемых при проектировании. Различают следующие классы бетона:
В – по прочности на сжатие (кубиковая прочность);Bt – по прочности на осевое растяжение. Под классом бетона по прочности на сжатие понимаютсреднестатистическоезначениевременногосопротивленияBm
(в МПа) сжатию эталонных образцов (кубы 15 15 15 см), изготовленных и испытанных через 28 сут, в соответствии с ГОСТом [25, 26].
В зависимости от вида и условий работы железобетонных конструкций нормами установлены следующие классы бетона по прочности на сжатие: В7,5–В60 [25, 26]. Высокие классы бетона (В30–В60) особенно целесообразно использовать в элементах предварительно напряженных конструкций и конструкций, работающих главным образом на сжатие, так как в этих случаях достигается существенный экономический эффект.
Для оценочного анализа НДС железобетонных оболочек в программном комплексе расчета оболочек можно задаваться приведенным начальным модулем упругости железобетона Еm:
Em = Eb V V−Vs + Es VVs ,
где Еb – модуль упругости бетона; Еs – модуль упругости арматур-
ной стали.
Если переписать этуформулу через соответствующие площади сечения единицы длины оболочки (единичной полосы) и площади сечения арматуры в ней для какой-то плоскости оболочки, ортого-
122 |
123 |

Математическое моделирование и расчет элементов строительных конструкций
нальной расположению рабочих стержней одного направления, получим более точное значение приведенного начального модуля упругости железобетона для этой плоскости:
Em = Eb A −AAs + Es AAs ,
где А – площадь единицы длины сечения оболочки; As – площадь
сечения арматуры в границах площади единицы длины сечения оболочки А.
4.8. О краевых условиях на контуре оболочки
Если в рассматриваемой задаче не нужно учитывать поперечные сдвиги, то уравнения равновесия (1.33) и функционал полной энергии деформации Э (1.27)будут содержать тринеизвестных функции U , V , W . На каждом краю оболочки задаются по четыре краевых условия: в перемещениях (геометрические условия) и усилиях (статические условия).
Если края оболочки опираются шарнирно неподвижно, то геометрические и статические краевые условия имеют вид:
при x = 0 и x = a U = V = W = 0; M x = 0;
при y = 0 и y = b U = V = W = 0; M y = 0 .
При жестком закреплении краев оболочки геометрические и статические краевые условия принимают вид:
при x = 0 и x = a U = V = W = 0; ∂∂Wx = 0; при y = 0 и y = b U = V = W = 0; ∂∂Wy = 0 .
4.9. Алгоритмы расчета напряженно-деформированного состояния пологих ребристых оболочек при учете нелинейности деформирования и ползучести бетона
Уравнения равновесия пологих ребристых оболочек с учетом нелинейности деформирования и развития деформаций ползучести представляют собой громоздкую систему интегро-дифференциаль-
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
ных уравнений восьмого порядка. Решение поставленной задачи вызывает существенные математические трудности.
Так как в функционале полной энергии деформации оболочки порядок производных искомыхфункций вдва раза ниже, чемв урав-
ненияхравновесия,токфункционалам Э= Эy −Эп или Э= Эy −Эc ,
записанным в безразмерных параметрах, применяется метод Ритца и находится система нелинейных алгебраических или интегроалгебраических уравнений. Нелинейность уравнений заключается в том, что напряжения нелинейно зависят от деформаций.
Применяется методика решения задачи, основанная на методе итераций [18]:
для уточнения начального упруго-линейного решения и получения нелинейно-упругого решения при каждом значении параметра нагрузки;
для нахождения деформаций ползучести при каждом значении параметра нагрузки и известном начальном решении линейноупругой задачи при последовательном изменении времени t.
4.9.1. Функционал полной энергии деформации пологой ребристой оболочки в безразмерных параметрах при учете нелинейности деформирования и ползучести бетона
Введем безразмерные параметры для оболочки |
9 : |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ξ= |
x |
|
, |
|
η= |
|
y |
, |
|
|
λ= |
|
|
a |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
= aU |
, |
|
|
|
|
|
|
|
|
|
b V |
, |
|
|
|
|
= W |
|
|
, |
|
|
|
|
|
|||||||||||||||
|
|
|
|
U |
|
V |
= |
W |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
h2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Kξ = |
|
a2K |
x , |
|
|
|
Kη |
= |
|
b2K y |
, |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a4q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
a = |
, F = |
|
, |
|
|
|
|
S = |
|
|
|
, |
|
|
|
J = |
|
|
, P = |
. |
||||||||||||||||||||||||||
h |
|
h |
|
|
|
|
h2 |
|
|
|
h3 |
|
Eh4 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2σ |
|
|
|
|
a2σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
σ = |
|
= |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.40) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
h2E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
124 |
125 |
Математическое моделирование и расчет элементов строительных конструкций
Используя безразмерные параметры (4.40), получим деформации εx ,εy ,γxy , функции изменения кривизн χ1 ,χ2 и кручения χ12 в виде:
εx = h2 εx , a2
εy = h2 λ2 εy , a2
εx = ∂∂ξU − KξW ;
εy = ∂∂Vη − KηW ;
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂U |
|
|
|
|
∂V |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
γxy = a2 λγxy , |
|
γxy = |
∂η |
+ |
∂ξ |
; |
|
|
|
|
|
|||||||||||||||||||||||||
|
h |
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
W |
|
|||||||||
χ = |
χ , |
χ = |
|
|
, |
|
|
|
|
= |
|
|
|
|
|
|
|
, |
|
|
|
|
= − |
; |
|||||||||||||||||
|
− |
|
|
|
|
|
|
|
χ |
2 |
|
|
λ χ |
2 |
|
χ |
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
1 |
a2 |
1 |
1 |
|
|
|
|
∂ξ2 |
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
∂η2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
χ12 = |
|
λχ12 , |
|
χ12 = − |
. |
|
|
|
|
|
|
|
|
(4.41) |
|||||||||||||||||||||||
|
|
|
|
a2 |
|
|
∂ξ ∂η |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Подставивдеформации εx ,εy ,γxy ,функцииизменениякривизн |
|||||||||||||||||||||||||||||||||||||||||
χ1,χ2 и кручения χ12 (4.41) в функционалы (4.24) и (4.25), (4.34), |
|||||||||||||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эy = |
E h5a b |
|
|
|
|
E h5a b |
|
|
|
|
Е h5 a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Эy , |
Эc = |
|
Эc , |
Эп = |
Эп, |
||||||||
2(1−µ2 )a4 |
|
2(1−µ2 )a4 |
|
2 (1−µ2 )a4 |
||||||||||
где
Эy = ∫∫1 1 {(1+ F )[εx2 + a1ε2y + a2εxεy + a3γ2xy ]+ S [2εxχ1 + a2εxχ2 +
00
+a2χ1εy + a6χ2εy + 4a7γxy χ12 ]+
+1 + J [χ2 + a1χ2 + a2 χ χ + 4a7χ2 ]−2 (1−µ2 )PW }dξ dη; (4.42)
12 1 2 1 2 12
Эп = 1∫∫1 {I1[εx2 + a1ε2y + a2εxεy + a3γ2xy ]+ I 2 [2εxχ1 +
0 0 |
|
|
|
|
]+ |
|
||
+ a2εxχ2 + a2χ1εy + a6χ2εy + 4a7γxy χ12 |
|
|||||||
+ |
|
3 [χ12 + a1χ22 + a2χ1 |
|
2 + 4a7 |
|
122 ]}dξ dη, |
(4.43) |
|
I |
χ |
χ |
||||||
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
Эc = ∫∫1 1 ∫t {[(1+ F )(εx2 + a1ε2y + a2εxεy )+
00 t0
+S (2εxχ1 + a2εx χ2 + a2χ1εy + a6χ2εy )+
+1 + J (χ2 + a χ2 + a χ χ )]R (t,τ)+
12 1 1 2 2 1 2 1
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
]R2 (t,τ)}dξ dη dτ. (4.44) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
+ [(1+ F )a3γxy + S4a |
7γxyχ12 |
+ |
|
|
+ J |
4a7χ12 |
||||||||||||||||||||
12 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь a = λ4 |
, |
a |
2 |
= 2µλ2 |
, |
a = µ λ2 |
, |
a |
6 |
= 2λ4 |
, |
a |
7 |
= µ λ2 . |
||||||||||||
1 |
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
1 |
||||||||
Запишем размерные параметры Ik в виде:
|
I = 4m |
(h + |
|
|
|
)b + |
Sb +(h3 + |
|
|
|
)b |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
F |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
I2 |
= |
4m |
|
|
|
|
|
|
+ ( |
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
3 |
Sb1 |
12 |
|
+Y )b2 + Kb3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
I |
|
= 4m |
(h3 |
+ |
|
|
)b + |
Kb +(h5 + |
|
|
|
|
|
|
)b |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 |
Y |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
12 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
h |
2 |
+H |
|
|
|
|
|
|
|
|
|
h |
2 |
+H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
+H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
+H |
|
|
|
|
|
|
h |
2 |
+H |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
F |
= ∫dz; |
|
S |
= |
|
|
∫Zdz; |
Y |
= |
|
|
|
|
|
∫Z |
2dz; |
|
|
K |
= |
|
|
|
|
|
∫Z 3dz; |
|
M |
= |
∫Z 4dz ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
h 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
h 2 |
|||||||||||||||||||
в безразмерных параметрах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
I1 |
, |
|
|
|
|
|
|
= |
|
I2 |
, |
|
|
|
3 = |
|
I3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
1 |
|
|
I |
2 |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
h3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
I1 |
= |
|
|
|
|
|
|
|
|
|
(1+ F)b1 + Sb2 + ( |
|
|
|
|
|
+ J )b3 |
; |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I 2 |
|
= |
|
|
|
|
|
|
|
|
Sb1 |
+( |
|
|
|
|
|
+ J )b2 |
|
+ Kb3 ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4m |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
I 3 = |
|
|
|
+ J )b1 + Kb2 +( |
|
|
|
|
+ M )b3 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(4.45) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
80 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
126 |
127 |

Математическое моделирование и расчет элементов строительных конструкций
где F = Fh , S = hS2 , J = hJ3 , K = hK4 , M = Mh5 .
Теперь
Эy = ∫∫1 1 {(1+ F )(εx2 + 2µλ2εxεy +λ4ε2y +µ1λ2γ2xy )+
00
+2S (εxχ1 +µλ2εxχ2 +λ4εy χ2 +µλ2εy χ1 + 2µ1λ2γxyχ12 )+
|
1 |
|
|
|
|
1 |
2 |
|
|
|
4 2 |
2 2 |
|||
|
|
|
|
||||||||||||
|
|
|
|||||||||||||
+ |
|
|
|
+ J (χ2 |
+2µλ χ1χ2 |
+λ χ2 |
+4µ1λ χ12 )− |
||||||||
12 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
− 2(1−µ2 ) |
|
|
|
}dξ dη ; |
(4.46) |
|||||
|
|
|
|
|
P |
W |
|||||||||
Эn = ∫∫1 1 {I1(εx2 +2µλ2εxεy +λ4ε2y +µ1λ2γ2xy )+
00
+2I2 (εxχ1 +µλ2εxχ2 +λ4εyχ2 +µλ2εyχ1 +2µ1λ2γxyχ12 )+
|
|
|
|
|
|
|
|
|
I3 |
( |
1 |
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
2 |
|
4 1 |
12 )}d d . |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
χ2 + |
|
µλ2 |
χ χ |
|
|
|
+λ4 |
χ2 + |
µ λ2 |
χ1 |
|
|
|
ξ |
η |
|
|
(4.47) |
||||||||||||||||||||||||||
|
|
|
1 |
2 |
|
|
|
|
4 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
1 2 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
b = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ε |
|
|
|
+λ ε |
|
|
+ λ ε |
|
|
|
ε |
|
+ |
|
λ γ |
= |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a 4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
x |
|
|
|
|
|
|
y |
|
|
|
|
x |
|
|
y |
|
|
|
xy |
a 4 1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
b z = |
|
1 |
|
|
z |
|
(2ε |
χ +2λ4ε |
|
|
χ +λ2ε |
χ +λ2ε |
χ +λ2γ |
|
χ |
)= |
1 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
zb |
; |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
a4 h |
|
|
|
x |
|
1 |
|
|
|
|
|
|
y |
|
|
2 |
|
|
x |
|
2 |
|
y |
1 |
|
|
|
xy |
12 |
a4 2 |
|||||||||||||||||||||
b3z2 = |
1 |
|
z2 |
|
(χ12 +λ4χ22 +λ2χ1χ2 +λ2χ122 )= |
1 |
z2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
b3 ; |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
a 4 |
h2 |
a 4 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ε = |
|
|
|
|
|
|
|
|
+ |
|
|
z |
+ |
|
|
|
z 2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
b |
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
i |
|
|
|
|
3 a 2 |
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
z = hz , a = ah .
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
4.9.2. Применение метода Ритца для получения интегро-алгебраических уравнений для ребристых пологих оболочек при решении задач ползучести
В соответствии с методом Ритца представим искомые функции U (ξ,η,t), V (ξ,η,t), W (ξ,η,t) в виде разложения в ряд:
N |
|
U = ∑U (I)X1(I)Y1(I); |
|
I =1 |
|
N |
|
V = ∑V (I)X 2(I)Y 2(I); |
(4.48) |
I =1 |
N
W = ∑W (I)X 3(I)Y3(I ).
I =1
Здесь U (I ), V (I ), W (I )~ – неизвестные функции переменной t; X1(I )− X 3(I )~ известные аппроксимирующие функции переменной ξ, удовлетворяющие при ξ = 0 , ξ =1 заданным краевым условиям; Y1(I )−Y3(I )~ известныеаппроксимирующиефункциипеременной η,
удовлетворяющие при η = 0, η =1 заданным краевым условиям.
В настоящем исследовании при шарнирно-неподвижном закреплении краев оболочки в качестве аппроксимирующих функций переменных выбраны синусы различных аргументов.
Подставим (4.48) в (4.40), (4.42) и, найдя производные от Э= Эy − Эc понеизвестнымчисловымпараметрамU ( ),V ( ),W ( ), приравняем их к нулю. В результате получим:
∫∫1 1 {(1+ F)[2εx X11( )Y1( )+ a2 εy X11( )Y1( )+ 2a3 γxy X11( )Y1( )]+
00
+S[2χ1X11( )Y1( )+ a2 χ2 X11( )Y1( )+4a7χ12 X1( )Y11( )]}dξdη =
= ∫∫1 1 ∫t {[(1+ F)(2εx X11( )Y1( )+ a2 εy X11( )Y1( ))+
0 0 t0
128 |
129 |

Математическое моделирование и расчет элементов строительных конструкций
+S(2χ1 X11( )Y1( )+a2 χ2 X11( )Y1( ))]R1(t,τ)+
+[(1 + F )2a3 γxy X1( )Y11( )+ S 4a7χ2 X1( )Y11( )]R1(t,τ)}dξdηdτ;
∫∫1 1 {(1+ F)[2a1εy X 2( )Y 21( )+a2 εx X 2( )Y 21( )+2a3 γxy X 21( )Y 2( )]+
0 0
+ S[a2 χ1 X 2( )Y 2( )+a6χ2 X 2( )Y 21( )+4a7χ12 X 21( )Y 2( )]}dξ dη= = ∫∫1 1 ∫t {[(1+ F)(2εx X11( )Y1( )+ a2 εy X11( )Y1( ))+
0 0 t0
+S(a2 χ1 X 2( )Y 21( )+ a6χ2 X 2( )Y 21( ))]R1(t,τ)+
+[(1+ F)2a3 γxy X 21( )Y 2( )+ S4a7χ12 X 21( )Y 2( )]R2 (t,τ)}dξdηdτ;
∫∫1 1 {(1+ F)[−2εx KξX 3( )Y 3( )−2a1εy KηX 3( )Y3( )−
0 0
−a2 εx KηX 3( )Y3( )−a2 εy KξX 3( )Y 3( )+
+S[2χ1Kξ X 3( )Y3( )−2εx X 32( )Y3( )−a2 χ2Kξ X 3( )Y3( )−
−a2 εx X 3( )Y3( )−a2 χ1KηX 3( )Y3( )−a2 εy X 32( )Y3( )−
−a2 χ2 KηX 3( )Y3( )−a6εy X 3( )Y32( )−4a7 γxy X 31( )Y31( )]+
+ (121 + J )[− 2χ1 X 32 ( )Y 3( ) −2aχ2 X 3( )Y 32 ( ) − a2 χ1 X 3( )Y 32 ( ) −
−a2 χ2 X 32( )Y 3( )− 4a7χ12 X 31( )Y 31( )]−
−2(1−µ2 )P X 3( )Y 3( )}dξdη = ∫∫1 1 ∫t {[(1+ F )(−2εx Kξ X 3( )Y 3( )−
00 t0
−2a1εy KηX 3( )Y 3( )−a2 εx KηX 3( )Y3( )−a2 εy KξX 3( )Y3( )]+
+S[−2χ1Kξ X 3( )Y3( )−a2 εx X 32( )Y3( )−a2 χ2 KξX 3( )Y3( )−
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
−a2 εx X 3( )Y32( )−a2 χ1KηX 3( )Y3( )−
−а2 εy X 32( )Y3( )−a6χ2KηX 3( )Y3( )−
−a6εy X 3( )Y32( )]+(121 + J )[−2χ1 X 32( )Y3( )−2a1 χ2 X 3( )Y32( )−
−a2 χ1 X 3( )Y32( )−a2 χ2 X 32( )Y3( )]R1(t,τ)+4Sa7 γxy X 31( )Y31( )+
+ ( |
1 |
+ |
|
)4a72 |
|
12 X 31( )Y31( )R2 (t,τ)dξdηdτ. |
(4.49) |
|||||||||||||
J |
χ |
|||||||||||||||||||
|
||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь в систему (4.49) вместо |
|
x , |
|
y , |
|
xy , |
|
1, |
|
2 , |
|
12 |
подста- |
|||||||
|
|
γ |
||||||||||||||||||
|
ε |
χ |
χ |
χ |
||||||||||||||||
ε |
||||||||||||||||||||
вим
εx = ∑N [U (I )X11(I )Y1(I )− KξW (I )X 3(I )Y 3(I )];
I=1
εy = ∑N [U (I )X 2(I )Y 21(I )−KηW (I )X 3(I )Y3(I )];
I=1
|
|
|
N |
|
||
|
|
|
xy = ∑[U (I )X1(I )Y11(I )+V (I )X 21(I )Y 2(I )]; |
|||
|
γ |
|||||
|
|
|
I=1 |
|
||
|
|
|
N |
N |
||
|
χ |
1 = −∑W (I )X 32(I )Y 3(I ); |
χ |
2 |
= −∑W (I )X 3(I )Y 32(I ); |
|
|
|
|
I =1 |
I =1 |
||
N
χ12 = −∑W (I )X 31(I )Y 31(I ).
I=1
Врезультате получим систему нелинейных интегро-алгебраи- ческих уравнений:
N
∑[U (I )CF1(I, )+V (I )CF 2(I, )+W (I )CF3(I, )]= F1 ( );
I=1
N
∑[U (I )CF 4(I, )+V (I )CF5(I, )+W (I )CF6(I, )]= F2 ( );
I=1
N
∑[U (I )CF 7(I, )+V (I )CF8(I, )+W (I )CF9(I, )]− CP( )P = F3 ( );
I=1
=1,2,…, N. (4.50)
130 |
131 |

Математическое моделирование и расчет элементов строительных конструкций
Здесь
N t
F1 ( )= ∑∫{[U (I )CC1(I, )+V (I )CC2(I, )+W (I )CC3(I, )]R1 (t,τ)+
I=1t0
+[U (I )CC4(I, )+V (I )CC5(I, )+W (I )CC6(I, )]R2 (t,τ)}dτ;
N |
t |
|
|
F2 ( )= ∑ |
∫{[U (I )CC7(I , )+V (I )CC8(I, )+W (I )CC9(I, )]R1 (t,τ)+ |
||
I =1t0 |
|
|
|
+[U (I )CC10(I, )+V (I )CC11(I, )+W (I )CC12(I, )]R2 (t,τ)}dτ; |
|
||
N |
t |
|
|
F3 ( )= ∑ |
∫{[U (I )CC13(I, )+V (I )CC14(I, )+W (I )CC15(I, )]× |
||
I =1t0 |
|
||
× R1(t,τ)+[U (I )CC16(I, )+V (I )CC17(I, )+W (I )CC18(I, )]× |
|||
× R2 (t,τ)}dτ. |
(4.51) |
||
4.9.3. Применение метода Ритца для получения нелинейных алгебраических уравнений для ребристых пологих оболочек при решении нелинейно-упругих задач
Подставим (4.48) в (4.40), (4.41) и, найдя производные от Э= Эy − Эп по неизвестным числовым параметрам U ( ), V ( ), W ( ), приравняем их к нулю. В результате получим:
1∫∫1 {(1+ F)[2εx X11( )Y1( )+ a2 εy X11( )Y1( )+ 2a3 γxy X11( )Y1( )]+
00
+S[2χ1X11( )Y1( )+ a2 χ2 X11( )Y1( )+4a7χ12 X1( )Y11( )]}dξdη =
=∫∫1 1 {I1[2εx X11( )Y1( )+ a2 εy X11( )Y1( )+ 2a3 γxy X1( )Y11( )]+
00
+I 2 [2χ1X11( )Y1( )+ a2 χ2 X11( )Y1( )+4a7χ12 X1( )Y11( )]}dξdη;
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
∫∫1 1 {(1+ F)[2a1εy X 2( )Y21( )+a2 εx X 2( )Y21( )+2a3 γxy X 21( )Y2( )]+
0 0
+S[a2 χ1X 2( )Y 2( )+ a6χ2 X 2( )Y 21( )+4a7χ12 X 21( )Y 2( )]}dξdη =
=∫∫1 1 {I1[2a1εy X 2( )Y 21( )+a2 εy X 2( )Y 21( )+2a3 γxy X 21( )Y 21( )]+
0 0
+I 2 [a2 χ1X 2( )Y 21( )+ a6χ2 X 2( )Y 21( )+4a7χ12 X 21( )Y 21( )]}dξdη;
∫∫1 1 {(1+ F)[−2εx KξX 3( )Y3( )−2a1εy KηX 3( )Y 3( )−
0 0
− a2 εx KηX 3( )Y3( )−a2 εy KξX 3( )Y3( )]+ S[2χ1KξX 3( )Y 3( )−
−2εx X 32( )Y3( )−a2 χ2Kξ X 3( )Y3( )−a2 εx X 3( )Y3( )− −a2 χ1KηX 3( )Y3( )−a2 εy X 32( )Y3( )−a2 χ2 KηX 3( )Y3( )− − a6εy X 3( )Y32( )−4a7 γxy X 31( )Y31( )]+
+(121 + J )[−2χ1 X 32( )Y 3( )−2aχ2 X 3( )Y32( )−a2 χ1 X 3( )Y32( )−
−a2χ2 X32( )Y3( )−4a7χ12X31( )Y31( )]−2(1−µ2 )PX3( )Y3( )}dξdη=
= ∫∫1 1 {I1[−2εx Kξ X 3( )Y 3( )−2a1 εy Kξ X 3( )Y3( )−a2 εx Kξ X 3( )Y3( )−
00
−a2 εy Kξ X 3( )Y3( )]+ I 2 [− 2χ1Kξ X 3( )Y3( )−2εx X 3( )Y3( )−
−a2 χ2 Kξ X 3( )Y3( )− a2 εx X 3( )Y32( )− a2 χ1KηX 3( )Y3( )−
−a2 εy X32( )Y3( )−a6χ2KηX 3( )Y3( )−
−a6εy X 3( )Y32( )−4a7 γxy X 31( )Y31( )]+ I 3 [−2χ1 X 32( )Y3( )−
−2aχ2 X 3( )Y32( )−a2 χ1X 3( )Y32( )−a2 χ2 X 32( )Y3( )−
− |
|
|
|
|
|
|
|
)]} |
− |
|
−µ2 |
|
|
|
|
|
|
ξ η |
(4.52) |
4a7 |
2 |
χ |
|
)Y31( |
|
2(1 |
)P X 3( |
|
)Y 3( |
|
|||||||||
|
12 X 31( |
|
|
|
|
|
|
)}d d . |
|||||||||||
132 |
133 |

Математическое моделирование и расчет элементов строительных конструкций
Теперь в систему (4.52) вместо εx , εy , γxy , χ1 , χ2 , χ12 нужно подставить
εx = ∑N [U (I )X11(I )Y1(I )− KξW (I )X 3(I )Y 3(I )];
I=1
εy = ∑N [U (I )X 2(I )Y 21(I )−KηW (I )X 3(I )Y3(I )];
I=1
|
|
|
N |
|
||
|
|
|
xy = ∑[U (I )X1(I )Y11(I )+V (I )X 21(I )Y2(I )]; |
|||
|
γ |
|||||
|
|
|
I=1 |
|
||
|
|
|
N |
N |
||
|
|
1 = −∑W (I )X 32(I )Y 3(I ); |
|
2 |
= −∑W (I )X 3(I )Y 32(I ); |
|
χ |
χ |
|||||
|
|
|
I =1 |
I =1 |
||
N
χ12 = −∑W (I )X 31(I )Y 31(I ).
I=1
Врезультате получим систему нелинейных алгебраических уравнений:
|
N |
[U (I )CF1(I, )+V (I )CF 2(I, )+W (I )CF 3(I, )]= П1 |
( ); |
|
|||
|
∑ |
|
|||||
|
I=1 |
|
|
|
|
|
|
|
N |
|
|
|
|
( ); |
|
|
∑[U (I )CF 4(I, )+V (I )CF5(I, )+W (I )CF 6(I, )]= П2 |
|
|||||
|
I=1 |
|
|
|
|
|
|
N |
[U (I )CF 7(I, )+V (I )CF8(I, )+W (I )CF9(I, )]− CP( ) |
|
|
|
|
( ); |
|
∑ |
P |
= П3 |
|||||
I=1 |
|
|
|
|
|
|
|
где |
|
=1,2,…,N , |
|
|
(4.53) |
||
|
|
|
|
|
|
|
|
П1( ) = ∫∫1 1 {I1[(2εx + a2 εy )b1 + 2a3 γxyb2 ]+ I 2 [(2χ1 + a2 χ2 )b1 + 0 0
+ 4a7 χ12b2 ]}dξdη;
П2 ( ) = ∫∫1 1 {I1[(2a1εy + a2 εx )b3 + 2a3 γxyb4 ]+ I 2 [(a2 χ1 + a6χ2 )b3 + 0 0
+ 4a7 χ12b4]}dξdη;
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
П3( )=−∫∫1 1 {I1[(2εxKξ +a2Kηεy )b5 +(2a1εyKη +a2εyKξ)b5]+
00
+I 2[(2χ1 +a2χ2 )Kξb5 +(a2 χ1 +a6χ2)Kµb5 +(2εx +a2εy )b6 +
+(a2εx +a6εy )b7 +4a7γxyb8]+I3[(2χ1 +a2χ2)b6 +
+ |
(a2 |
|
|
+ |
2a1 |
|
2 )b7 |
+ |
8a7 |
|
12b8]}d |
ξ |
η |
(4.54) |
|
|
χ |
χ |
χ |
||||||||||||
|
1 |
|
|
|
|
d , |
|
||||||||
где b1 = X1′( )Y1( ), |
b2 = X1( )Y1′( ), b3 = |
X 2( )Y 2 ( ), |
|
||||||||||||
b4 = X 2′( )Y 2( ),b5 = X 3( )Y 3( ), b6 |
|
|
′ |
|
|||||||||||
= X 3 ( )Y 3( ), |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
b7 = X 3( )Y 3′′( ), b8 = X 3′( )Y 3′( ).
При использовании метода упругих решений А. А. Ильюшина [7] двойные интегралы П1 ÷П3 будут вычисляться при извест-
ных значениях εx ,εy ,γxy ,χ1,χ2 , χ12 .
4.9.4.Методика решения нелинейных алгебраических
иинтегро-алгебраических уравнений
Кратко системы (2.13) и (2.16) запишем в виде: |
|
|||||||
|
|
|
|
Fу(X ) − f P = D (X ) , |
(4.55) |
|||
где D (X )= Fn (Х), |
если решаются физически нелинейные задачи, |
|||||||
или D (X )= Fс(Х), |
|
если решаются задачи ползучести. |
|
|||||
Здесь Fу(X )− f P − левые части системы (2.13) или (2.16); |
||||||||
F (X )= (П ,П |
2 |
,П |
3 |
)Т ; |
F (X ) |
= (F ,F ,F )Т ; |
|
|
п |
1 |
|
|
с |
1 2 3 |
|
||
X = [U (I ),V (I ),W (I )]T . |
|
|
||||||
Для линейно-упругой задачи при нагрузке P = Р1 |
находится |
|||||||
решение линейного уравнения: |
|
|
||||||
|
|
|
|
|
Fу(X )− f P1 = 0. |
(4.56) |
||
Для нахождения нелинейно-упругого решения при некоторой |
||||||||
нагрузке |
P = Р решается итерационная задача Fу(Xi )− f P1 = |
|||||||
|
1 |
|
|
|
|
|
|
|
= Fп(Xi−1 ) до тех пор, пока предыдущее решение не будет отличать-
134 |
135 |

Математическое моделирование и расчет элементов строительных конструкций
ся от последующего на величину заданной погрешности. За X 0 берется решение линейно-упругой задачи при P1 .
При решении задачи ползучести Fс(X ) представляется в виде:
t |
|
(X( τ))R2 (t,τ)]dτ. |
|
Fс(X )= ∫[Ф1 |
(X (τ))R1(t,τ)+Ф2 |
(4.57) |
В работе В. Иt0. Климанова и С. А. Тимашева [12] применяется следующая методика.
Отрезок интегрирования [t0 ,tk ] разобьем на частичные отрезки [ti−1,ti ] с шагом ∆ t (в дальнейшем шаг по t будем брать ∆ t = 1 сутки)
|
k |
ti |
|
F (X )=∑ |
∫[Ф1 (X( τ))R1 (tk ,τ)+ Ф2 (X( τ))R2 (tk ,τ)]dτ. |
(4.58) |
|
с |
i=1 ti−1 |
|
|
|
|
||
На каждом частичном отрезке интеграл вычислим приближен- |
|||
но по формуле прямоугольников |
|
||
|
ti |
|
|
|
∫[Ф1(X( τ))R1(tk ,τ)+Ф2 (X( τ))R2 (tk ,τ)]dτ ≈ |
|
|
|
ti−1 |
|
|
≈ [Ф1(X(ti−1 ))R1(tk ,ti−1 )+Ф2 (X(ti−1 ))R2 (tk ,ti−1 )]∆ t. |
(4.59) |
||
Обозначим R1 = R1(tk ,ti−1 )∆t , R2 = R2(tk ,ti−1 )∆t . Таким образом, Fс(X ) при t = tk будет иметь вид:
F (X )=∑k [Ф1(X(ti−1 )) |
|
1 +Ф2 (X(ti−1 )) |
|
2 ]. |
|
R |
R |
(4.60) |
с i=1
Аналогичная замена интеграла интегральной суммой при
расчете оболочек использовалась в работах В. И. Климанова и С. А. Тимашева [12], В. В. Карпова [9].
При решении задачи ползучести при некоторой нагрузке P1 вначаленаходитсярешениелинейно-упругойзадачи X (t0 ). Затем это решение подставляется в Fс(X ) и решается опять-таки линейноупругая задача с известной правой частью в линейных алгебраических уравнениях. Итерационный процесс по временной координате t можно записать в виде:
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
Fу(Xi ) − f P1 = Fc (Xi−1). |
(4.61) |
Процесс по временной координате t продолжается до тех пор, покапрогибненачнетрезковозрастать.Время, прикоторомэтопроисходит, будет определено как критическое время tкр .
4.10. Программа расчета пологих ребристых оболочек при учете ползучести и физической нелинейности бетона
Алгоритм расчета пологих ребристых оболочек при учете ползучести и физической нелинейности бетона реализован в виде программного комплекса для ЭВМ [Свидетельство о государственной регистрации программы для ЭВМ, № 2011613074 PologObolochka, 18 апреля 2011 г.]. Программный комплекс PologObolochka составлен в соответствии с тематикой гранта «Аналитическая ведомственнаяцелеваяпрограмма»МинистерстваобразованияинаукиРФ«Развитие научного потенциала высшей школы (2009–2010 гг.)», тема № 2.1.2/6146.
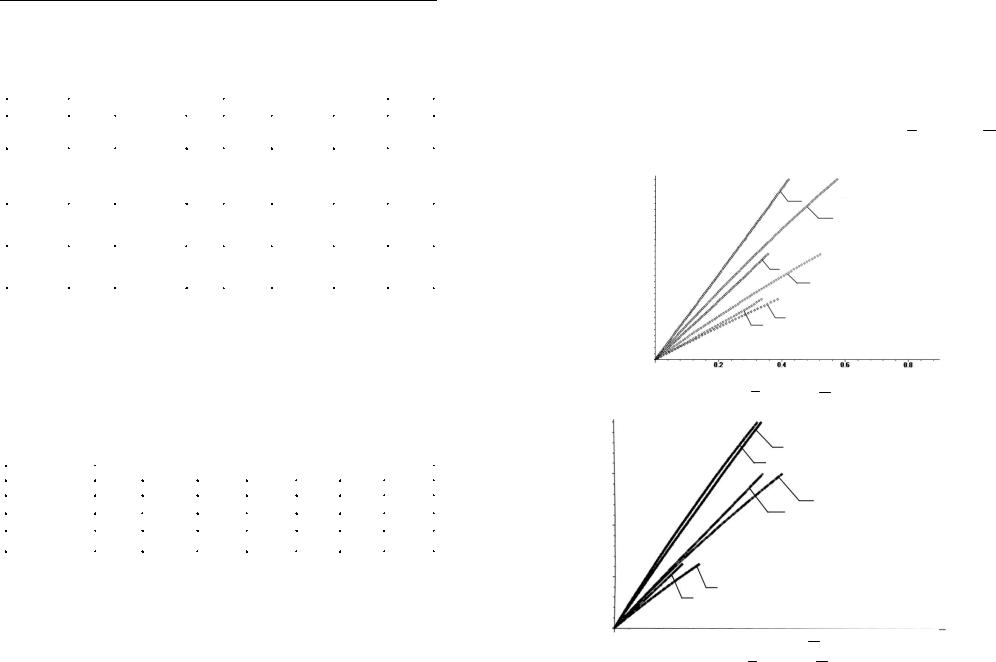
ПрограммныйкомплексPologObolochkaнаписанвсредеDelphi 7 на языке Object Pascal, реализован в виде консольного приложения, чтобы не тратить лишнюю память на вывод графической информации. Все результаты вычислений выводятся в отдельные текстовые файлы. Графики строятся в Maple 7 по данным из текстовых файлов. Наиболее характерные результаты расчетов оболочек приведенывсоответствующихразделахдиссертации.Крометого,врамкахгрантаразработанапрограмма исследованияребристыхпологих оболочек с учетом геометрической нелинейности.
4.11. Прочность пологих железобетонных ребристых оболочек при линейно-упругом деформировании
4.11.1. Реальные варианты оболочек и их безразмерные параметры
Так как все решения целесообразно проводить в безразмерных параметрах, в табл. 4.3 представлены размерные параметры для некоторых реальных вариантов оболочек и соответствующие им безразмерныепараметры.Используяформулыпереходаотбезразмерных
136 |
137 |
Математическое моделирование и расчет элементов строительных конструкций
параметров к размерным, можно получить все характеристики НДС для конкретных вариантов оболочек и конкретных видов материала.
Таблица 4.3
Размерныеибезразмерные параметрыоболочекразныхвариантов
Номер |
Размерные параметры, м |
|
Безразмерные параметры |
Стрела |
|||||||||||||||||||||||||
варианта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подъ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K ξ = K η |
|||||
а= b |
|
|
R = R1 = R2 |
|
h |
|
|
|
|
|
R = R1 = R2 |
|
|
||||||||||||||||
оболочки |
|
|
|
|
a = b |
|
|
|
|
ема d |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
54 |
|
|
135,9 |
|
|
0,09 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
36 |
|
|
90,6 |
|
|
0,06 |
|
|
|
|
|
1510 |
|
|
|
238 |
|
29,75h |
||||||||||
|
27 |
|
|
67,95 |
|
|
0,045 |
|
|
600 |
|
|
|
|
|
||||||||||||||
|
18 |
|
|
45,3 |
|
|
0,03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
II |
36 |
|
|
90,6 |
|
|
0,18 |
|
|
200 |
|
503 |
|
|
|
79,5 |
|
10h |
|||||||||||
|
27 |
|
|
67,95 |
|
|
0,135 |
|
|
|
|
|
|
|
|||||||||||||||
|
18 |
|
|
45,3 |
|
|
0,09 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
III |
27 |
|
|
67,95 |
|
|
0,27 |
|
|
100 |
|
251,5 |
|
|
|
39,76 |
|
5h |
|||||||||||
|
18 |
|
|
45,3 |
|
|
0,18 |
|
|
|
|
|
|
|
|||||||||||||||
|
13,5 |
|
34 |
|
|
0,135 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь a = |
а |
, |
|
|
= R , |
|
ξ = |
a2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
h |
|
|
|
h |
|
hR1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В табл. 4.4 приводятся расчетные сопротивления сжатию и растяжению бетона и модули упругости для разных классов бетона [25, 26].
Таблица 4.4
Расчетныесопротивлениясжатиюирастяжениюбетона(призменные прочности)имодулиупругости
Параметр |
|
Класс бетона по прочности на сжатие |
|
|||||
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
||
|
||||||||
Rb , МПа |
14,5 |
17,0 |
19,5 |
22,0 |
25,0 |
27,5 |
30,0 |
|
Rbt , МПа |
1,05 |
1,20 |
1,30 |
1,40 |
1,45 |
1,55 |
1,60 |
|
Eb 10−4 , МПа |
3,0 |
3,25 |
3,45 |
3,60 |
3,75 |
3,90 |
3,95 |
|
4.11.2. Допускаемые нагрузки для различных вариантов оболочек
При проведении вычислительного эксперимента рассматриваются квадратные в плане пологие оболочки, имеющие шарнирнонеподвижное закрепление по контуру и находящиеся под действием
138
Глава 4. Расчетпологих ребристых оболочек при учете физической нелинейности ...
равномерно-распределенной поперечной нагрузки. Оболочки могут быть гладкими (без ребер) либо подкрепленными шестью (по три ребра в каждом направлении) или 18 (по девять ребер в каждом на-
правлении) регулярно расположенными ребрами высотой 3h и шириной 2h , направленными параллельно осям координат.
Нарис.4.3–4.5вкачествепримеровсрезультатамирасчетакон-
кретных оболочек представлены графики «нагрузка Р – прогиб W » для оболочек вариантов I, II, III соответственно.
120 000
|
|
|
|
|
|
31 |
|
|
|
||
100 000 |
|
|
3 |
|
|||||||
80 000 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
60 000 |
|
2 |
|
|
|
||||
40 000 |
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
20 000 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|||
0,2 |
0,4 |
|
|
|
|
0,6 |
0,8 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
Рис. 4.3. График «нагрузка Р – прогиб W » для оболочки варианта I
8000
3
31
6000
|
|
|
21 |
2 |
|
|
|
P |
|
|
|
||||
4000 |
|
|
|
|
|
||
2000 |
1 |
1 |
|
|
|
||
0 |
1 |
|
|
|
|
||
|
|
|
|
||||
0,2 |
0,4 |
0,6 |
0,8 |
||||
|
|
||||||
W
Рис. 4.4. График «нагрузка Р – прогиб W » для оболочки варианта II
139
