Справочник школьника по математике. 5-11 кл_Маслова Т.Н, Суходский А.М_2008 -672с

АЛГЕБРА

§ 12. Виды функций

40. Функция возрастает на промежутке (0, + ¥)

ïðè a > 1, убывает на (0, + ¥) при 0 < a < 1.

50. Îñü Îó является вертикальной асимптотой графика (если a > 1, òî y ® -¥ ïðè x ® 0, à åñëè 0 < a < 1, òî y ® +¥ ïðè x ® 0 ).

a) á)

Ðèñ. 41

График функции y = loga x можно получить из графика функции ó = àõ с помощью преобразования симметрии относительно прямой ó = õ. Íà ðèñ. 41, à построен график логарифмической функции для a > 1, à íà ðèñ. 41, á — äëÿ 0 < a < 1.

117. Число å. Функция ó = åõ. Функция y = lnx. Среди показательных функций ó = àõ, ãäå

a > 1, особый интерес для математики и ее приложений представляет функция, обладающая следующим свойством: касательная к графику функции

151

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

(см. п. 224) в точке (0; 1) образует с осью Îõ угол 45° (рис. 42). Основание à такой функции ó = àõ принято

обозначать буквой å, ò. å. ó = åõ. Подсчитано, что å = = 2,7182818284590..., и установлено, что å — иррациональное число, которое можно представить как следующую сумму:

Именно с помощью этого равенства и находят значе- ние числа å с любой точностью.

Функцию ó = åõ иногда называют экспонентой. Логарифмическую функцию, обратную экспонен-

òå ó = åõ, т. е. функцию y = loge x, принято обозна- чать y = ln x (где ln читается: «натуральный ло-

гарифм»). Графики функций ó = åõ è y = ln x симметричны относительно прямой ó = õ (ðèñ. 43).

152

АЛГЕБРА

§12. Виды функций

118.Определение тригонометрических функций.

Тригонометрические функции определяются с помощью координат вращающейся точки. Рассмотрим на координатной плоскости õÎó единичную окружность, т. е. окружность единичного радиуса с цент-

ром в начале координат. Обозначим через Ð0 точку единичной окружности с координатами (1; 0), эту точ- ку будем называть начальной. Возьмем произволь-

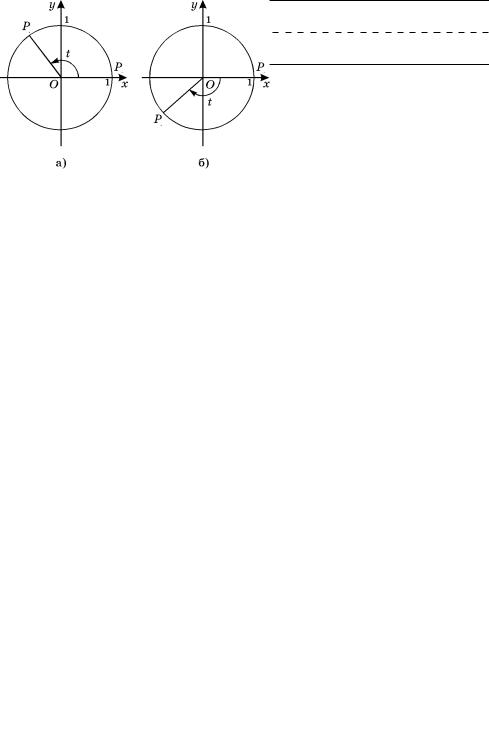
ное число t и повернем начальную точку относительно точки Î íà óãîë t ; ïðè ýòîì åñëè t > 0, то поворот осуществляется в направлении против часовой стрелки (рис. 44, à), à åñëè t < 0, — то по часовой

стрелке (рис. 44, á).

В результате поворота получим на единичной окружности точку Pt. Ее ордината называется синусом числа t и обозначается sint, а абсцисса — косинусом числа t (èëè óãëà t ) и обозначается cos t.

t

0 0

153

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

Тангенсом числа t называется отношение синуса числа t к его косинусу:

tg t = sin t . cos t

Котангенсом числа t называется отношение косинуса числа t к его синусу:

ctg t = cos t . sint

Приведем таблицу значений синуса, косинуса, тангенса и котангенса некоторых углов:

Из определений следует, что не существует тангенс углов, косинус которых равен нулю, и котангенс углов, синус которых равен нулю.

Говоря о синусе, косинусе, тангенсе и котангенсе числа, используют как градусную, так и радианную меру угла (см. п. 254):

154

АЛГЕБРА

§ 12. Виды функций

Функции y = sinx, y = cosx, y = tgx, y = ctgx

называют тригонометрическими функциями.

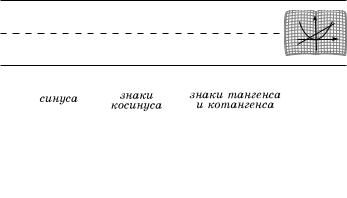
119. Знаки тригонометрических функций по чет-

вертям. Поскольку sin t è cos t — это соответственно ордината и абсцисса точки Ðt единичной окружности с центром в начале координат (см. п. 118), синус положителен для точек, лежащих на верхней полуокружности, и отрицателен для точек, лежащих на нижней полуокружности; косинус положителен для точек, лежащих на правой полуокружности, и отрицателен — на левой полуокружности. Знаки всех тригонометрических функций по четвертям единичной окружности указаны на рис. 45.

120. Исследование тригонометрических функций

на четность, нечетность. Точки Pt è P-t единичной

155

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

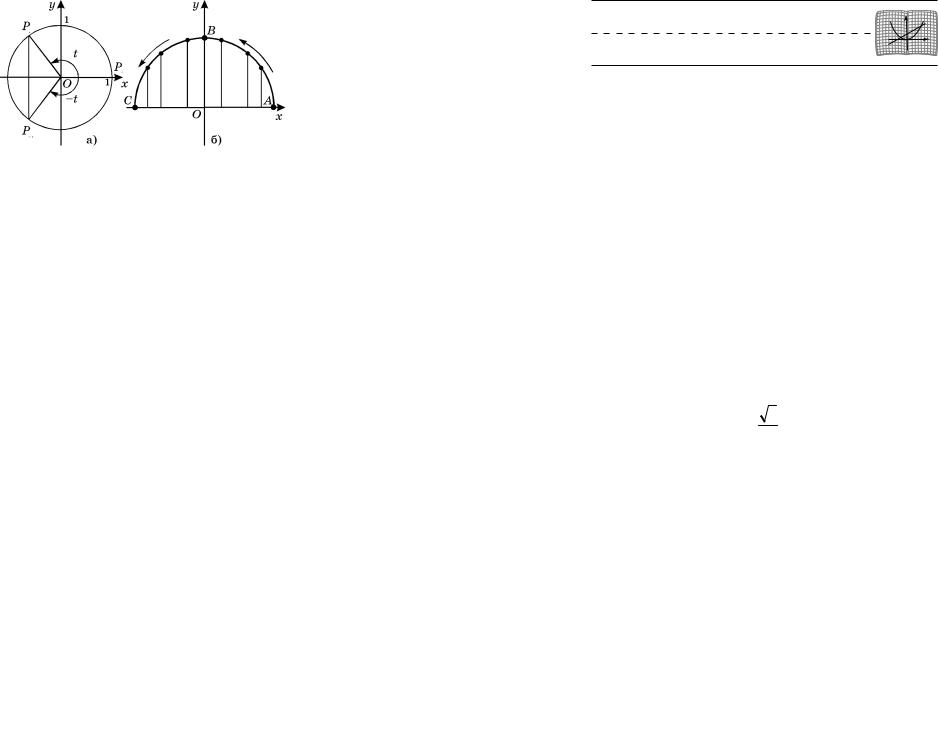
окружности имеют одинаковую абсциссу и противоположные (отличающиеся друг от друга лишь знаком) ординаты (рис. 46). Это значит, что cos (–t) =

= cost, sin (–t) = –sin t, ò. å. y = cos x — четная, а y = sin x — нечетная функция. Функции y = tg x, y = ctg x — нечетные.

121. Периодичность тригонометрических функций.

Òàê êàê Ðt è Ðt + 360° — одна и та же точка единичной окружности (см. п. 118), то синусы соответствующих

углов, а также их косинусы равны. Значит,

sin (x + 360°) = sin x, cos (x + 360°) = cos x, Более общими являются равенства

sin (x + 360°k) = sin x, cos (x + 360°k) = cos x,

ãäå k — любое целое число.

Если аргумент õ выражен в радианах, то

sin (x + 2pk) = sin x, cos (x + 2pk) = cos x, k Î Z.

t

0

– t

156

АЛГЕБРА

§ 12. Виды функций

Для функций y = tg x è y = ctg x справедливы равенства

tg(x + pk) = tg x, ctg(x + pk) = ctg x, k Î Z.

Таким образом, любое число вида 2pk является периодом функций sin x, cos x, а число вида pk — периодом функций tg x, ctg x. При этом 2p — основной период sin x, cos x, а p — основной период tgx, ctgx (ñì. ï. 96).

Используя свойства четности, нечетности, периодичности, можно тригонометрическую функцию интересующего нас угла свести к тригонометрической функции угла, заключенного в пределах от 0° äî 180°.

П р и м е р. Вычислить sin 945°.

q Имеем sin 945° = sin (720° + 225°) = sin (225° + + 360° · 2) = sin 225° = sin (225° – 360°) = sin (–135°) = = –sin135°.

Далее, sin 135° = sin (180° – 45°) = sin 45°

10. Область определения — множество R.

20. Множество значений — отрезок [–1, 1].

30. Функция периодическая; основной период равен 2p .

40. Функция нечетная.

157

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

Взяв контрольные точки (0; 0), (p / 6; 1/ 2), (p /2; 1), (p; 0), построим график функции y = sin x

на отрезке [0, p] . Так как функция y = sin x нечетная, то, отобразив построенный график симметрично относительно начала координат, получим график функ-

ции на отрезке [-p, p] . Наконец, воспользовавшись

периодичностью функции y = sin x , можно построить график на всей области определения (рис. 48).

123. Свойства и график функции y = cos x. Исследование функции y = cos x проводится аналогич-

Ðèñ. 48

158

АЛГЕБРА

§ 12. Виды функций

но исследованию функции y = sin x (ñì. ï. 122). Ïå-

речислим свойства функции y = cos x :

10. Область определения — множество R.

20. Множество значений — отрезок [–1, 1].

30. Функция периодическая с основным перио-

äîì 2p.

40. Функция четная.

50. Функция убывает на промежутках [2pn, p + +2pn] и возрастает на промежутках [-p + 2pn, 2pn],

n Î Z.

График функции y = cos x изображен на рис. 49.

124. Свойства и график функции y = tg x.

10. Область определения: x ¹ p + pk, k Î Z. 2

20. Множество значений — вся числовая прямая.

30. Функция периодическая с основным периодом p.

Ðèñ. 49

159

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

60. Прямые x = p + pk, k Î Z — вертикальные 2

асимптоты.

Выбрав контрольные точки (0; 0), (p / 4; 1), (p / 3; 3), строим график функции y = tg x на промежутке [0, p / 2). Далее, используя нечетность функции y = tgx , построим график в интервале (-p / 2, p / 2). Наконец, воспользовавшись периодич-

ностью функции y = tgx , построим график на всей области определения (рис. 50).

Ðèñ. 50

160