Справочник школьника по математике. 5-11 кл_Маслова Т.Н, Суходский А.М_2008 -672с

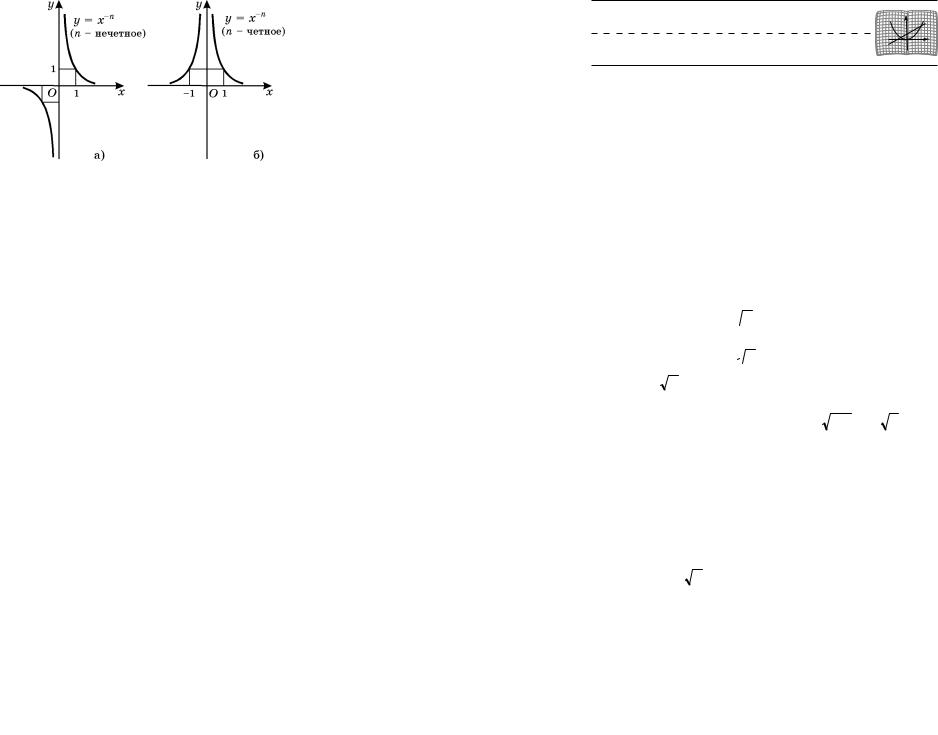
АЛГЕБРА

§ 12. Виды функций

Ðèñ. 31

Нанесем полученные точки на координатную плоскость и соединим их плавной кривой. Получим

график функции y = x (ðèñ. 31, à).

108. Функция y = 3 x. Перечислим свойства функции y = 3 x :

10. Область определения — вся числовая прямая. 20. Функция нечетная, так как 3 - x = - 3 x.

30. Функция возрастает на всей числовой прямой. Для построения ветви графика при x ³ 0 составим таблицу значений функции: x = 0, y = 0; x = 1,

y = 1; x = 4, y = 1,6; x = 8, y = 2.

Нанесем полученные точки на координатную плоскость и соединим их плавной кривой; затем к построенной ветви добавим ветвь, симметричную ей относительно начала координат. Получим график

функции y = 3 x (ðèñ. 31, á).

141

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

функция y = n x обладает теми же свойствами, что и функция y = 3 x (см. п. 108), а ее график напоминает график функции y = 3 x (ðèñ. 32, á).

Ðèñ. 32

110. Степенная функция с положительным дроб-

ным показателем. Рассмотрим функцию y = xr, ãäå r — положительная несократимая дробь. Перечислим некоторые свойства этой функции:

10. Область определения — луч [0, + ¥). 20. Функция ни четная, ни нечетная.

30. Функция возрастает на [0, + ¥).

142

АЛГЕБРА

§ 12. Виды функций

2

y = x3

–12

На рис. 33 изображен график функции y = x5/2.

Он заключен между графиками функций y = x2 è

y = x3, заданных на промежутке [0, + ¥). Подобный

вид имеет график любой функции вида y = xr , ãäå r > 1.

На рис. 34 изображен график функции y = x2/3. Подобный вид имеет график любой степенной функ-

öèè y = xr, ãäå 0 < r < 1.

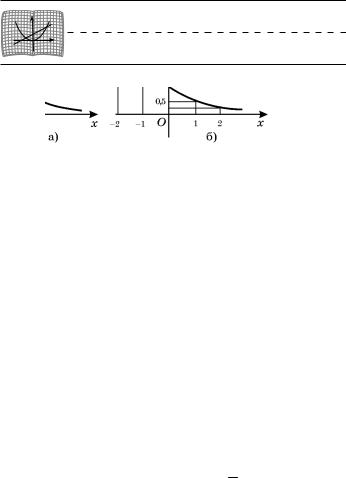
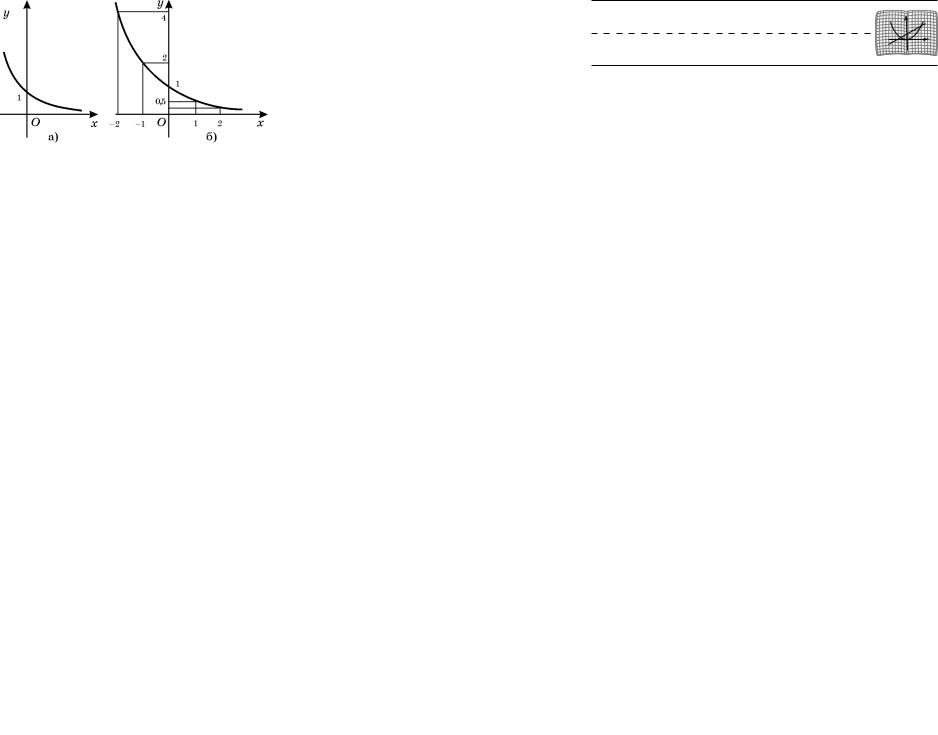
111. Степенная функция с отрицательным дроб-

ным показателем. Рассмотрим функцию y = x-r, ãäå r — положительная несократимая дробь. Пере- числим свойства этой функции:

10. Область определения — промежуток (0, + ¥). 20. Функция ни четная, ни нечетная.

30. Функция убывает на (0, + ¥).

143

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

На рис. 34 изображен график функции y = x-1/2. Подобный вид имеет график любой функции y = xr, ãäå r — отрицательная дробь.

112. Функция y = [x]. Построим график функции y = [x] (ñì. ï. 33). Åñëè 0 £ x < 1, òî y = [x] = 0; åñëè 1 £ x < 2, òî y = [x] = 1; åñëè -1 £ x < 0, òî

y = [x] = -1 и т.д. График функции y = [x] изображен на рис. 35.

113. Функция y = {x}. Построим график функции y = {x} (см. п. 33). Заметим, что для любого x

выполняется двойное равенство {x - 1} = {x} = {x + 1}.

Это значит, что y = {x} — периодическая функция с периодом T = 1.

Åñëè 0 £ x < 1, òî [x] = 0, а потому

{x} = x - [x] = x. Построив график функции y = {x}

на промежутке [0, 1) и перенеся его параллельно на расстояния n (n — натуральное число) влево и впра-

144

АЛГЕБРА

§ 12. Виды функций

во вдоль оси Îõ, получим график функции y = {x} на всей числовой прямой (рис. 36).

114. Показательная функция. Показательная функция задается формулой y = ax, ãäå a > 0 è a ¹ 1.

Перечислим свойства функции y = ax ïðè a > 1 : 10. Область определения — вся числовая прямая. 20. Множество значений — луч (0, + ¥).

30. Функция не является ни четной, ни нечетной.

Это следует из того, что a-x ¹ ax è a-x ¹ -ax.

40. Функция возрастает на всей числовой прямой.

50. Îñü Ox является горизонтальной асимптотой графика при x ® -¥.

График функции y = ax ïðè a > 1 выглядит так, как показано на рис. 37, à. Например, на рис. 37, á

изображен график функции y = 2x.

Ðèñ. 37

145

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

y = ax; 0 < a < 1

Перечислим свойства функции y = ax ïðè

0 < a < 1 :

10. Область определения — вся числовая прямая. 20. Множество значений — луч (0, + ¥).

30. Функция не является ни четной, ни нечетной. 40. Функция убывает на всей числовой прямой. 50. Îñü Ox является горизонтальной асимптотой

графика при x ® +¥.

График функции y = ax ïðè 0 < a < 1 выглядит так, как показано на рис. 38, à. Например, на рис. 38, á

æ 1 öx

изображен график функции y = ç ÷ .

è 2 ø

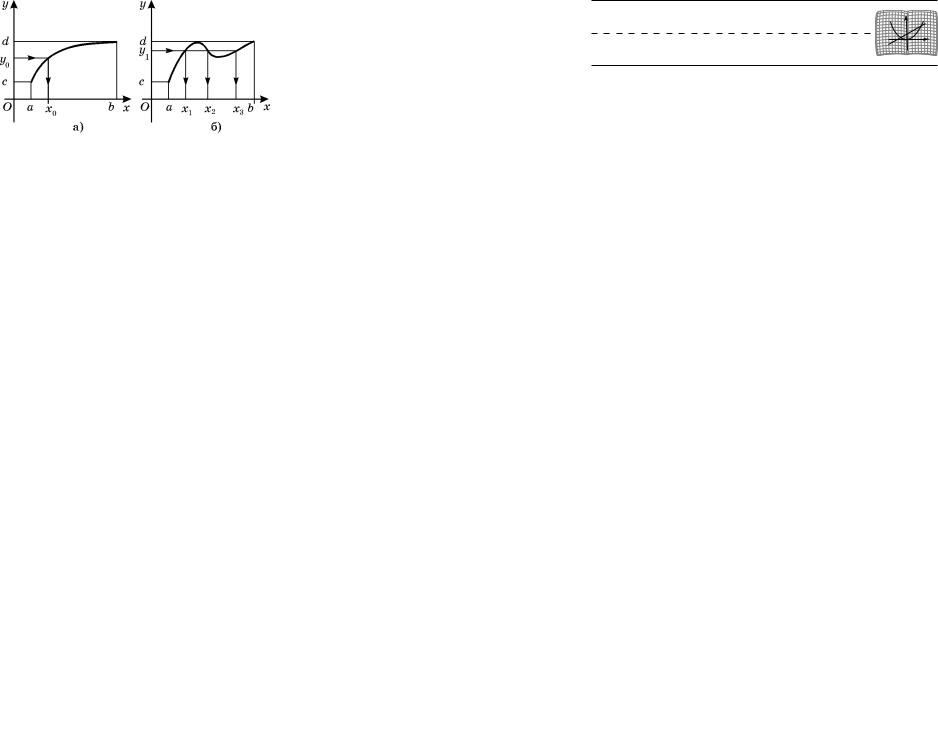
115. Обратная функция. График обратной фун-

êöèè. Сравним две функции y = f(x) è y = g(x). Их графики изображены на рис. 39, à è á. Обе они определены на отрезке [a, b], а их множеством зна- чений является отрезок [c, d]. Первая функция об-

146

АЛГЕБРА

§ 12. Виды функций

ладает следующим свойством: для любого y0 из отрезка [c, d] åñòü только одно значение x0 из отрезка

[a, b] такое, что f(x0) = y0. Геометрически указан-

ное свойство означает, что любая горизонтальная прямая, пересекающая ось Oy между точками ñ è d, ïå-

ресекает график функции y = f(x) только в одной точке. Вторая функция этим свойством не облада-

ет: например, для значения y1 прямая y = y1 ïåðå-

секает график функции y = g(x) в трех точках. Зна- чит, в первом случае при каждом фиксированном

y0 из отрезка [c, d] уравнение f(x) = y0 имеет только один корень õ0, а во втором случае при некоторых

ó, например при ó = ó1, уравнение g(x) = y1 имеет более одного корня.

Если функция y = f(x) такова, что для любого ее

значения ó0 уравнение f(x) = y0 имеет относитель-

íî õ единственный корень, то говорят, что функция f

обратима.

Так, функция y = f(x), график которой изобра-

æåí íà ðèñ. 39, à, обратима, а функция y = g(x), график которой изображен на рис. 39, á, необратима.

Можно сказать и так: функцию, принимающую каждое свое значение в единственной точке области определения, называют обратимой.

Если функция f обратима, то, выразив õ èç ôîð-

ìóëû y = f(x) и поменяв затем õ è ó местами, полу- чим обратную функцию. Таким образом, если фун-

êöèÿ f задана формулой y = f(x), то для нахожде-

147

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

Ðèñ. 39

ния обратной функции нужно решить уравнение f(x) = y относительно õ, а затем õ è ó поменять местами. Заметим, что если для некоторых ó из множества значений функции f это уравнение имеет более одного корня, то обратной функции нет.

Сравнивая графики функций y = f(x) è y = g(x)

(ñì. ðèñ. 39, à è á), замечаем, что y = f(x) — возрастающая функция (и у нее есть обратная функция), тогда как функция y = g(x) не является ни возрастающей, ни убывающей (и у нее нет обратной функции). Возрастание или убывание функции обеспечивает существование обратной функции.

Ò.3.4. Если функция y = f(x) определена и возрастает (или убывает) на промежутке Х и множеством ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает (или убывает) íà Y.

П р и м е р. Доказать, что функция ó = 2õ – 1 имеет обратную, и найти ее.

148

АЛГЕБРА

§ 12. Виды функций

q Функция ó = 2õ – 1 возрастает на всей числовой прямой, значит, у нее есть обратная функция. Чтобы найти эту обратную функцию, надо решить уравнение

2õ – 1 = ó относительно õ. Имеем x = 0,5 (y + 1). Ïî-

меняв õ è ó местами, получим y = 0,5(x + 1). Это и есть искомая обратная функция. n

Если точка (õ; ó) принадлежит графику функции y = f(x), то точка (ó; õ) принадлежит графику обратной функции. Поэтому график обратной функции

получается из графика функции y = f(x) с помощью преобразования плоскости õÎó, переводящего точку (õ; ó) в точку (ó; õ). Этим преобразованием является симметрия относительно прямой ó = õ.

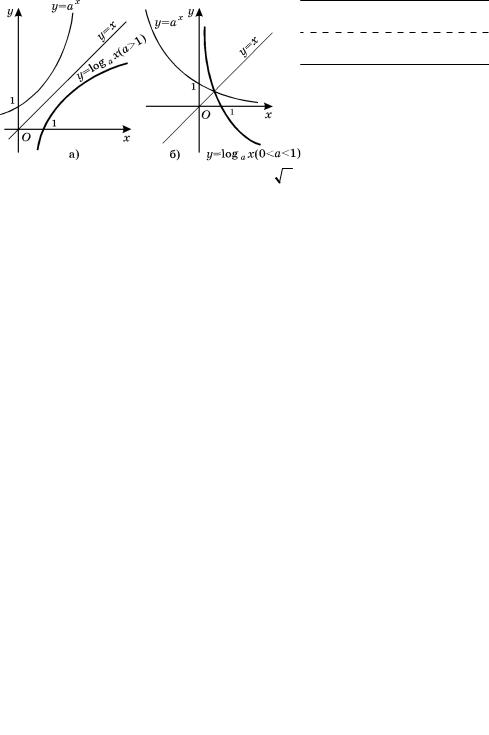
Таким образом, чтобы построить график функции, обратной функции y = f(x), надо график функ-

öèè y = f(x) преобразовать симметрично относительно прямой у = õ (ðèñ. 40, à).

Ðèñ. 40

149

АЛГЕБРА

Раздел III. ФУНКЦИИ И ГРАФИКИ

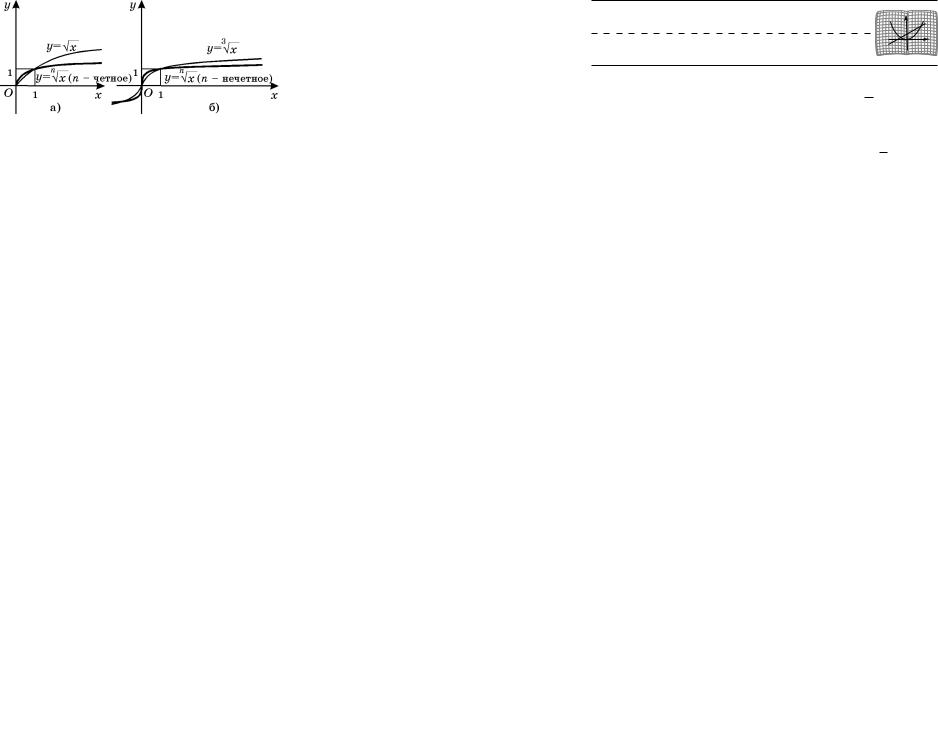
Например, если y = xn, ãäå x ³ 0, n — натураль-

íîå, n > 1, òî x = n y. Поменяв õ è ó местами, полу- чим y = n x. Графики двух взаимно обратных функ-

öèé y = xn è y = n x симметричны относительно прямой ó = õ (ðèñ. 40, á).

116. Логарифмическая функция. Показательная функция ó = àõ, ãäå a > 0, a ¹ 1, обладает всеми

свойствами, которые гарантируют существование обратной функции (см. теорему 3.4): 1) область определения — вся числовая прямая; 2) множество

значений — промежуток (0, + ¥); 3) функция ó = àõ

возрастает при a > 0 и убывает при 0 < a < 1. Указанные свойства обеспечивают существование

функции, обратной показательной, определенной на (0, + ¥) и имеющей в качестве множества своих зна- чений всю числовую прямую.

Эта обратная функция обозначается так: y = = loga x (читается: «логарифм числа õ по основанию à»). Èòàê, логарифмическая функция y = loga x,

ãäå a > 0 è a ¹ 1, — это функция, обратная показательной функции ó = àõ.

Логарифмическая функция y = loga x обладает следующими свойствами (они вытекают из теоремы 3.4):

10. Область определения — луч (0, + ¥) .

20. Множество значений — вся числовая прямая.

30. Функция ни четная, ни нечетная.

150