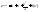- •(1)Понятие непрерывности функции.Свойства непрерывных функций.
- •Свойства функций:
- •1) Общие свойства
- •2) Односторонняя непрерывность
- •3) Непрерывность монотонной и обратной к строго монотонной функции
- •(2)Непрерывность элементарных функций
- •1) Основные элементарные функции
- •(3) Теоремы Больцана-Каши о промежуточных значениях
- •(4) Открытые и замкнутые множества на числовой прямой
- •2) Признаки открытости и замкнутости множеств
- •(5)Компакт.Критерии компакта.
- •(6)Теоремы Вейерштрасса о непрерывных функциях.
- •1) Теоремы Вейерштрасса о непрерывных функциях
- •(8)Классификация разрывов функции
- •1) Формула для приращения функции
- •3) Производная сложной функции
- •(12)Связь между существованим производной и касательной
- •1)В задаче 2 (5.1) фактически было доказано, что если
- •Связь между существованием односторонней касательной и существованием односторонней производной (с той же стороны) такая же как и двусторонней.
- •3) Связь между дифференциированностью, наличием конечной производной и непрерывностью
- •3)Дифференциал сложной функции и его эквивалентность.
- •(15)Производные высших порядков.Формула Лейбница.
- •1)Понятие производной высшего порядка
- •3)Формула Лейбница для производных высшего порядка от произведения
- •(24) Признаки монотонности и постоянства функций
- •(25)Правило Лопеталя
- •2) Необходимый признак экстремума
- •3) Достаточные признаки эктремума
- •(30) Асимптоты к графику функции.Построение графиков с использованием производных.
- •Построение графика функции с использованием производных:
3) Связь между дифференциированностью, наличием конечной производной и непрерывностью
Если
функция дифференцируема в

 она имеет конечную производную и поэтому
непрерывна.
она имеет конечную производную и поэтому
непрерывна. функция
непрерывна
функция
непрерывна
 Функция
дифференциированна
Функция
дифференциированна

 конечная
конечная
 функция
непрерывна
функция
непрерывна
(14)Основные формулы и правила вычисления дифференциалов
1)Поскольку
в случае дифференцированности функции
 ,
то каждая формула для вычисления
производных сразу дает формулу для
вычисления дифференциала.
,
то каждая формула для вычисления
производных сразу дает формулу для
вычисления дифференциала.
2)Теорема:
Если f(x)
и g(x)
дифференцируемы
в ,
то
,
то
1)

2)

3)
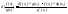
3)Дифференциал сложной функции и его эквивалентность.
Теорема: Пусть
1)
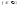 ,
,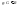 ;z=g(y)
и y=f(x)
;z=g(y)
и y=f(x)
2)
f(x)
- дифференцируемf
в ,a
g(x)
в
,a
g(x)
в
 ,
, ,
,
тогда
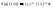 (1) или
(1) или (2)
(2)
Доказательство: Следует из теоремы производной сложной функции.
Как видно из формулы 2, формулу для дифференциала сложной функции, где у- промежуточная переменная, такая же как и если бы у была окончательная переменная, это и есть инвариантностью(неизменностью).
Формальной разницы между формулами 1 и 2 нет, а фактическая есть:
z=g(y)
y=f(x)
 ,
где
,
где

z=g(y),
у-независимая
переменная.
 ,
где
,
где -приращение
функции.
-приращение
функции.
Инвариантность часто используют при решении.
Пример:
 sinx=y,
sinx=y,
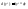 ,
где
,
где ,
,
(15)Производные высших порядков.Формула Лейбница.
1)Понятие производной высшего порядка
Рассмотрим функцию
y=f(x),
пусть она дифференцируема при всех х,
тогда
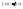 -
это тоже функция. Производная
-
это тоже функция. Производная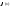 называется второй производной функцииf(x).
Обозначается
называется второй производной функцииf(x).
Обозначается
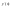 ,
,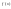 ,
,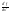 .
.
По определению
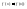 .
.

2)Формулы для вычисления производных высшего порядка
1)
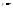
 ,
,
 ,
,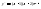 ,
,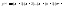
2)
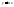
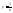 ,
,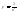 ,
,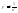 ,
,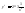 ,
,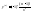
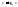 ,
,
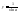 ,
,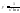
3)
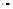
 ,
,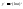 ,
, ,
,
 ,
,
4)

 ,
, ,
, ,
,
 ,
, ,
,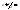 ,
,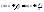 ,
,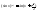
5)

 ,
,

3)Формула Лейбница для производных высшего порядка от произведения
Пусть f(x)
и g(x)
имеют все производные до n-ого
порядка, включительно

 ,
,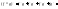
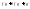 ;
;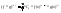 ,
где
,
где
Пример:
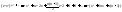
(16) Дифференциалы высших порядков
1) Пусть f(x)
имеет
произвольные всех требуемых порядков,
тогда
 (1),
где
(1),
где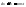 ,
таким образом,dy-
это функция от x
, и она имеет
конечную производную, то есть снова
дифференцируема
,
таким образом,dy-
это функция от x
, и она имеет
конечную производную, то есть снова
дифференцируема
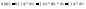 ,
, (2),dx
каждый раз
брали одинаковый.
(2),dx
каждый раз
брали одинаковый.
 -
второй дифференциалу.
-
второй дифференциалу.
n-ый
дифференциал:
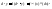
2) Отсутствие инвариантности дифференциалов высшего порядка.
Рассмотрим функцию z=g(y), где y=f(x) – в силу инвариантности первого дифференциала dz можно вычислить, как и в случае если бы y - была независимая переменная.
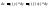 ,
в свою очередь
,
в свою очередь
 ,
то естьdy
– функция
от х.
,
то естьdy
– функция
от х.
Найдем второй дифференциал.
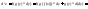 дифференциал
первого порядка будем вычислять
пользуясь инвариантностью, как будто
у
независимая переменная
дифференциал
первого порядка будем вычислять
пользуясь инвариантностью, как будто
у
независимая переменная
 (3)
(3)
Сравнивая 3 и 2,
видим, что выражения, если у
– не конечная,
для второго дифференциала не совпадает,
в 3 мы получаем лишнее слагаемое, которое
в общем случае не равно 0
 второй
дифференциал не обладает инвариантностью.
второй
дифференциал не обладает инвариантностью.
Частный случай:
z=g(y)
y=kx+b
dy=k*dx=const
, то есть
 формулы
2 и 3 совпадут.
формулы
2 и 3 совпадут.
3) Следуя формуле
для n-ого
дифференциала и зная n-ую
производную можно вычислить и n-ый
дифференциал
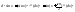
(17)Теорема Ферма.
Определение.
Пусть f : E→
R;
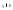 (
( -
внутренняя дляE).
-
внутренняя дляE).
f(x)
называется строго возрастающей
(убывающей) в т. относительноE,
если
относительноE,
если
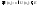 и
и выполняется, что
выполняется, что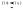
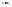 выполняется, что
выполняется, что
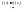
Лемма.
Если
 внутренняя точка области определения
функции, то при
внутренняя точка области определения
функции, то при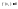 f(x)
строго возрастает в
f(x)
строго возрастает в ,
а при
,
а при f(x) строго убывает в
f(x) строго убывает в .
.
Доказательство.
Пусть
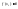 .
.
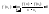 ,
т.е. числитель и знаменатель имеют
одинаковые знаки
,
т.е. числитель и знаменатель имеют
одинаковые знаки
 функция возрастает.
функция возрастает.
Замечание.
Лемма доказывается для внутренних точек, если бы речь шла о краевых точках, то лемма тоже сохраняется, но возрастание и убывание будут односторонними.
Теорема Ферма.(о нуле производной).
Если f(x) определена
на <a,b> и принимает наибольшее
(наименьшее) значение в некоторой
внутренней т с, то если


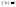
Доказательство.
Пусть в c – наибольшее
значение

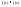
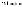 (1).
(1).
(от противного).
Пусть

 пусть
пусть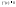 ;
значит :
;
значит :
a)
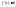
 по лемме в т. с функция возрастает т.е.
по лемме в т. с функция возрастает т.е.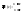
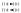 (2)
(2)
что противоречит (1)
б)

 функция убывает т.е.
функция убывает т.е.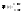
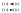 (3)
(3)
что противоречит (1).
(2) и (3) противоречат
(1)
 ч.т.д.
ч.т.д.
(18) Теорема Роля.
Если f(x) : 1) непрервна на замкнутом [a,b]
2) имеет f’(x) в (a,b)
3) f(a)=f(b)
То
 т.
т.
Доказательство.
Возможны 2 случая:
a)
f(x)=const
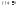
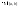
б)
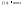 ,
тогда по теореме Вейерштрасса (функция
непрерывна на компакте)
,
тогда по теореме Вейерштрасса (функция
непрерывна на компакте)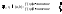 т.е.
т.е.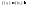 согласно условию 3 хотя бы одно из этих
значений принимается внутри промежутка,
обозначим т.с (соответствующее этому
значению). Тогда по теореме Ферма f'(c)=0
согласно условию 3 хотя бы одно из этих
значений принимается внутри промежутка,
обозначим т.с (соответствующее этому
значению). Тогда по теореме Ферма f'(c)=0
(19)Теорема Лагранжа.
Теорема.
Если f(x) : 1) непрерывна в [a,b]
2) дифференцируема в (a,b)
Тогда
 т.
т.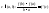 (1)
(1)
Доказательство.
Сведем данную теорему к теореме Роля. (осадим график вниз на величину d(x)).
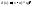
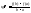
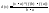
Итак, введем
вспомогательную функцию
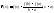
 непрерывна
в [a,b], дифференцируема в (a,b)
непрерывна
в [a,b], дифференцируема в (a,b)
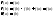
Значит функция
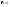 удовлетворяет
всем условиям теоремы Роля.
удовлетворяет
всем условиям теоремы Роля.
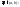
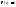 ;
т.е.
;
т.е.

Геометрический смысл теоремы.
Теорема утверждает,
что
 т.е. угол наклона касательной в т.с равен
углу наклона хорды AB, значит касательная
в т.с параллельна хорде .
т.е. угол наклона касательной в т.с равен
углу наклона хорды AB, значит касательная
в т.с параллельна хорде .
Формулу (1) называют
формулой конечного приращения Лагранжа
и записанной в виде :
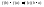 где
где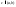
(20)Теорема Коши.
Если f(x) и g(x) :
1)непрерывны в [a,b]
2)имеют конечные производные в (a,b)
3)g'(x) 0
и конечна
0
и конечна
Тогда
 т. с
т. с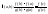 (1)
(1)
Доказательство.
a) Покажем, что
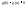 .
.
Если доказевается противное, то g'(x)=0 согласно теореме Роля
такого условия (g(b)-g(a)=0) быть не может, что противоречит условию.
б) Введем вспомогательную функцию
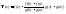
Утверждение, что удовлетворяет условия теоремы Роля

Значит
 т.с
т.с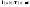
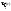
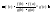 получаем формулу
(1).
получаем формулу
(1).
Ясно, что теорема
Лагранжа является частным случаем
теоремы Коши, которая получается при
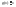 /
/
В литературе теоремы Ферма, Ролля, Лагранжа и Коши часто называют теоремами о среднем.
(21)Формула Тейлора для многочлена.
10. Формула Тейлора для многочлена.
Рассмотрим произвольный многочлен n-ой степени.
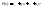 (1)
(1)
Возьмем любое
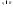 .
Этот многочлен всегда можно записать
по степеням
.
Этот многочлен всегда можно записать
по степеням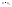 .
Для этого x представляется в виде
.
Для этого x представляется в виде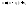 и подставляется в (1). При этом
и подставляется в (1). При этом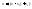 то по формуле бинома Ньютона, после
чего все выражение группируем по
степеням.
то по формуле бинома Ньютона, после
чего все выражение группируем по
степеням.
В результате
получится
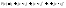

Найдем коэффициент
 .
.
Для этого положим
в



Продифференцируем
формулу
 .
.
Получим
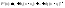
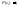

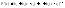

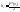

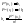
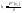 (3)
(3)
По формуле
 коэффициент
коэффициент могут вычислять по формуле (3)
могут вычислять по формуле (3)
 можно записать в
виде:
можно записать в
виде:
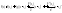
Формула Тейлора для многочлена n-ой степени.
Замечание.
Если многочлен
записать в виде
 ,
то его коэффициенты выражаются по
формуле (3) и наоборот: если
,
то его коэффициенты выражаются по
формуле (3) и наоборот: если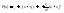 то производные
то производные
(22)Формула Тейлора для функции.
Для функции.
Пусть y=f(x), в т. имеет все необходимые производные. Для
приращения функции
имеет все необходимые производные. Для
приращения функции или
или
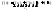

Многочлен справа
дает приближение функции f(x)
на величину
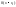
Многочлен
 обладает тем свойством, что его значение
в т.
обладает тем свойством, что его значение
в т. и значение его первой производной в т.
и значение его первой производной в т. совпадают с таковыми для самой функции.
совпадают с таковыми для самой функции.
Возникает гипотеза,
что многочлен n-ого порядка
 ,
значение которого
,
значение которого и производные
и производные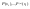 совпадают с таковыми для самой функции,
даст еще большее приближение.
совпадают с таковыми для самой функции,
даст еще большее приближение.
Такой многочлен можно расписать так:
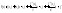 (4)
(4)
Многочлен Тейлора
n-ой
степени для функции f(x)
с центром в
 .
.
Теперь обозначим
разницу

Получим :
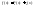
т.е.
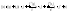 (5)
(5)
Формула Тейлора
для функции n-ого п орядка с центром в
т и остаточным (дополнительным) членом
и остаточным (дополнительным) членом
Теорема.
Пусть f(x) имеет
производные
 в <a,b>, причем
в <a,b>, причем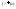 существует и конечна в (a,b). Тогда для
остаточного члена формула Тейлора (5)
для любого фиксированного
существует и конечна в (a,b). Тогда для
остаточного члена формула Тейлора (5)
для любого фиксированного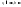 справедливо:
справедливо:
1)
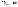

где
 - константа,
- константа,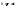 (Форма остаточного члена Шлёмиха-Роша)
(Форма остаточного члена Шлёмиха-Роша)
2)
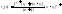
Форма Лагранжа
3)

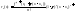
Форма Каши
Замечание 1.
Суть формулы
Тейлора состоит в том, что она дает
приближенное значение функции с точность
до
 через простое выражение (многочлен) с
коэффициентом, выраженным через функцию
и её производные.
через простое выражение (многочлен) с
коэффициентом, выраженным через функцию
и её производные.
Замечание 2.
Форма для остаточного
члена Лагранжа легко запоминается,
т.к. представляет собой следующий за
n-ым член многочлена Тейлора. Только
производная взята не в
 ,
а в промежуточной точке
,
а в промежуточной точке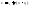
Замечание 3.
Формулу Тейлора
для функции при
 называют формулой Маклорина
называют формулой Маклорина
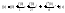
Замечание 4.
Формула Тейлора с остаточным ч леном в форме Лагранжа превращается в формулу конечного приращения Лагранжа
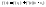
(23)Применение формулы Тейлора для разложения некоторых функций.
10. Для разложения некоторых функций.
Все разложения будем рассматривать по формуле Маклорина.
А)
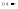

(1)
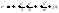
Б)
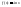

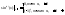
(2)
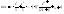
В)
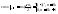
(3)
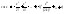
Г)
 ;
;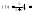 ;
;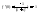 ;
;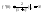 ;
;
(4)
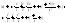
(5)
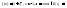
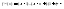

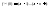
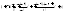
Если бы
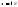 ,
то остаточный член
,
то остаточный член ,
включающий согласно теореме из 6.5 (n+1)
производную был бы равен 0 и мы бы
получили новый вывод формулы бинома
Ньютона.
,
включающий согласно теореме из 6.5 (n+1)
производную был бы равен 0 и мы бы
получили новый вывод формулы бинома
Ньютона.
Замечание.
Теорема.
Если
 ,a
,a
 неприрывна в
неприрывна в ,то
,то
(6)
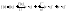
где
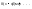 при
при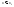 ,
т .е.
,
т .е.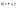 является остаточным членом, который
называется остаточным членом в форме
Пеано.
является остаточным членом, который
называется остаточным членом в форме
Пеано.
Формула Тейлора с остаточным членом в форме Пеано является обобщением формулы приращения функции, т.е.
 получаем из формулы (6) при n=1
получаем из формулы (6) при n=1
Если
в формулах 1,2,4,5
 взять в форме Пеано, то увидим, что все
они дают более точные, чем известные
нам ранее выражения эквивалентности
функций
взять в форме Пеано, то увидим, что все
они дают более точные, чем известные
нам ранее выражения эквивалентности
функций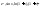
20. Для вычисления значения некоторых функций.
Рассмотрим
формулу Тейлора при
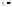 с остаточным членом в форме Лагранжа
с остаточным членом в форме Лагранжа
(7)
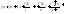
Если отбросить в (7) дополнительный член, то получим приближенную формулу
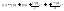
заменяющую в общем случае произвольную функцию целым многочленом. При этом можно оценить погрешность формулы, т.к. она равна по абсолютной величине отброшенному члену. Н-р: если (n+1) производная (по крайней мере при изменении аргумента от 0 до x ограничена по абсолютной величине числом М, то
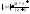
Рассмотрим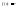
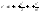
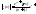
тогда
при x>0
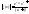
В
частности при x=1
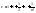
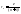
30. Для вычисления пределов.
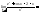 //
в знаменателе б.м.ф. порядок 3, поэтому
достаточно взять до 3 порядка по формуле
Маклорина с остаточным членом в форме
Пеано.//
//
в знаменателе б.м.ф. порядок 3, поэтому
достаточно взять до 3 порядка по формуле
Маклорина с остаточным членом в форме
Пеано.//
40. Для разложения более сложных функций.
Полученное разложение по формуле Тейлора (Маклорина) можно использовать для разложения более сложных (составных) функций.
Н-р:
 до x2
до x2