(5)Компакт.Критерии компакта.

Определение:

Множество E называется компактом, если из любой последовательности точек этого множества можно выделить подпоследовательность, сходящуюся в точке из этого же множества

Теорема (критерий компактов):

Для того чтобы множество E было компактом необходимо и достаточно чтобы оно было замкнутым и ограниченным.

Доказательство:

Пусть E – компакт.

Ограниченность:

Пусть Е – неограниченно сверху, тогда 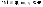, значит из нее нельзя выделить подпоследовательность сходящуюся в точке из Е, отсюда следует что Е – не компакт, получим противоречие, значит Е – ограниченно

Замкнутость:

т.к. Е – не компакт, то можно выделить из последовательности подпоследовательность, которая будет сходится в какой нибудь точке из множества Е,с другой стороныт.к.- предел всей последовательности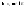, получается взяв любую предельную точку для Е, получается что Е – замкнутое

Е – замкнуто и ограниченно , т.к. Е ограниченно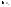ограниченнопо лемме Б.Б. из нее можно выделить сходящуюся подпоследовательность, но учитывая, что Е – замкнутое по критерию замкнутости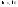

(6)Теоремы Вейерштрасса о непрерывных функциях.

1) Теоремы Вейерштрасса о непрерывных функциях

Лемма 1:

Если непрерывна на компакте Е, то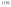- тоже компакт

Доказательство:

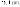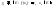Рассмотрим и, для каждого изизможно выделить сходящуюся подпоследовательность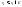, а т.к. функция непрерывна на У, то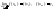Получаемт.е. множество- компакт

Лемма 2:

Если G – компакт, то - ограниченно,, возьмем последовательность чисел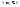по критериюsup, , ноG – замкнуто по критерию замкнутости

Первая, вторая теоремы Вейерштрасса:

Всякая непрерывная на компакте функция: 1) неограниченна на нем

2) достигает на нем свои набольшее и наименьшее значения

Доказательство:

1) Т.к. Е – компакт, то по лемме 1 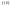тоже компакт, т.е. ограниченна

2) По лемме 2 , т.е. есть точка являющаясяsup и есть точка inf

(7)Равномерная непрерывность ф ункции. Теорема Кантора о равномерной непрерывности

Рассмотрим непрерывную на Е, т.е.

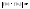
Ясно, что для различных точек - различно, если можно подобратьподходящее сразу для всех точек, то функция называется равномерной, непрерывной.

Определение:

Функция 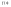называется равномерной, непрерывной на Е, если для любого,

Ясно, что для любая равномерная непрерывная функция будет и просто непрерывной, такое что 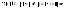,обратное – не верно.

Пример:

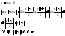
Есть частный случай, когда из непрерывности следует равномерная непрерывность.

Теорема (Кантора о равномерной непрерывности):

Всякая непрерывная на компакте функция равномерно непрерывна на нем.

Доказательство:

Фиксируем Пусть не существуетдля которого бы выполнялись условия равномерной непрерывности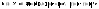

Возьмем последовательность не отрицательных чисел 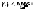По предположению (1)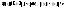По лемме Б. Б. из ограниченной последовательностиможно выделить подпоследовательность сходящуюся в некоторой точке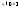Будем считать что уже сама последовательностьсходится к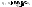Т.к., тоВ виду того, что- непрерывнаа это противоречит тому, чтонепрерывная на компакте функция равномерно непрерывна