(2)Непрерывность элементарных функций

1) Основные элементарные функции

а) 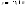непрерывна

б) 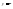по следствию св. 6

в)

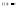
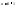
строго монотонна, непрерывная на всей области определения.

г) непрерывна как обратная к строго монотонной

д) тригонометрические функции: на этом промежутке функция строго монотонна, т.к. на любом таком промежутке она монотоннався непрерывная

Непрерывная, как композиция двух непрерывных

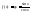
Непрерывная как отношение двух непрерывных функций. Так же и

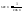
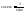
е) обратные тригонометрическим:

непрерывные как обратные к строго монотонным определенных на промежутке

2) Поскольку все элементарные функции получены из основных элементарных с помощью конечного числа арифметических и алгебраических действий и т.к. операции над непрерывными функциями снова приводят к непрерывным функциям, то все элементарные функции являются непрерывными во всех точках области определения.

(3) Теоремы Больцана-Каши о промежуточных значениях

1) Определение (непрерывность на языке последовательности):

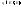называется непрерывной в точке относительно множества, где, если

Теорема 1:

Если: 1) f(x) – непрерывна на [a,b]

2) f(x) принимает на концах промежутка значения разных знаков, тогда

Доказательство:

Пусть f(a)<0, f(b)>0

Точкой d рассечем отрезок ab пополам. Получим [a,d] и [d,b] в одном из промежутков функция будет меньше нуля на левом конце и больше нуля на правом. Обозначим этот промежуток . Снова рассечем его пополам. Получим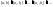

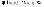, т.к. функция в точке с непрерывна, то по определению непрерывности

2) Теорема 2:

Если: 1) f(x) – непрерывна на [a,b]

2)

Доказательство:

Введём вспомогательную функцию - непрервна

Замечание:

Ни одно из требований теоремы нельзя нарушить.

(4) Открытые и замкнутые множества на числовой прямой

1) Определение 1:

Точка называется внутренней для множестваE, если принадлежит ему вместе с некоторой окрестностью.

Определение 2:

Множество E называется открытым, если любая его точка является внутренней для этого множества.

Определение 3:

Множество E называется замкнутым, если если оно содержит все свои конечные предельные точки

Есть множества не являющимися ни открытыми ни замкнутыми, есть множества которые одновременно являются и открытыми и замкнутыми.

2) Признаки открытости и замкнутости множеств

Для любого множества E, его дополнением (CE) называется множество , т.е. множество всех точек не принадлежащихE.

Теорема 1:

1. Для того чтобы множество было открытым необходимо и достаточно, чтобы его дополнение CE было замкнутым

2. Для того чтобы E было замкнутым необходимо и достаточно, чтобы CE было открытым

Доказательство:

Пусть E открыто и покажем, что CE замкнуто, тогда любая точка E принадлежит E вместе с некоторой окрестностью, из этого следует, что в этой окрестности нет точек из CE, т.е. все предельные для E точки принадлежат CE отсюда следует, что CE замкнуто.

Теорема 2 (критерий замкнутости множеств):

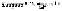
Доказательство:

E – замкнутое;

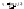
1)

2) 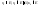, т.е. случай 2) места не имеет

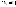рассмотрим последовательность вложенных окрестностей т.к.- предельная дляE, то в каждой из этих окрестностей

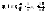
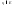по (3) точка , т.е.E замкнуто.