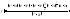(30) Асимптоты к графику функции.Построение графиков с использованием производных.

Асимптоты к графику функции:

Определение:

Прямую называют асимптотой для некоторой кривой, если при удалении вдоль кривой в бесконечность расстояние между прямой и кривой стремится к нулю.

Определение 1:

Прямая , называется вертикальной асимптотой к графику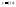, если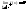

Определение 2:

Прямая , называется правой (левой) наклонной асимптотой к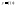, если

Для практического нахождения асимптот служит теорема:

Теорема (критерий наклонной асимпт):

Для того, чтобы прямая была правой (левой) наклонной асимптотой для графика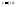необходимо и достаточно чтобы:

1.

2.

Доказательство:

1) Необходимость:

- правая наклонная асимптота. Тогда для нее справедливо (1), т.е.

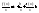выполнено условие 1

выполнено условие 2

1) Достаточность:

Выполним условия 1 и 2 теоремы для некоторой прямой . В таком случае из условия 2 следуетА это означает равенство (1), т.е. прямая является некоторой асимптотой

Пример:

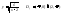
1) вертикальная асимптота

2) ;

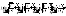
3)

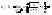
Построение графика функции с использованием производных:

Можно рекомендовать следующую схему при построении графиков:

1) Найти область определения, характерные особенности (чет, нечет, периодичность и точки разрыва);

2) Найти точки пересечения графика с осями координаты и промежутки знака постоянства функции;

3) По первой производной найти промежутки монотонности, точки подозрительные на экстремум, исследовать их (если это удобно, с помощью первой производной);

4) По второй производной найти промежутки определенного направления вогнутости, точки подозрительны на перегиб и исследовать их; если необходимо, продолжить исследовать на экстремум подозрительный точки с помощью старших производных;

5) Найти вертикальные и наклонные асимптоты;

6) Вычислить значения функции в найденных характерных точках и исследовать поведение функции в точка разрыва и граничных точках;

7) Результаты снести в таблицу при этом возможно взять несколько дополнительных точек и построить график.

Пример:

1) ;

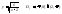2)

3) ;;

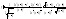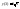4)