
- •(1)Понятие непрерывности функции.Свойства непрерывных функций.
- •Свойства функций:
- •1) Общие свойства
- •2) Односторонняя непрерывность
- •3) Непрерывность монотонной и обратной к строго монотонной функции
- •(2)Непрерывность элементарных функций
- •1) Основные элементарные функции
- •(3) Теоремы Больцана-Каши о промежуточных значениях
- •(4) Открытые и замкнутые множества на числовой прямой
- •2) Признаки открытости и замкнутости множеств
- •(5)Компакт.Критерии компакта.
- •(6)Теоремы Вейерштрасса о непрерывных функциях.
- •1) Теоремы Вейерштрасса о непрерывных функциях
- •(8)Классификация разрывов функции
- •1) Формула для приращения функции
- •3) Производная сложной функции
- •(12)Связь между существованим производной и касательной
- •1)В задаче 2 (5.1) фактически было доказано, что если
- •Связь между существованием односторонней касательной и существованием односторонней производной (с той же стороны) такая же как и двусторонней.
- •3) Связь между дифференциированностью, наличием конечной производной и непрерывностью
- •3)Дифференциал сложной функции и его эквивалентность.
- •(15)Производные высших порядков.Формула Лейбница.
- •1)Понятие производной высшего порядка
- •3)Формула Лейбница для производных высшего порядка от произведения
- •(24) Признаки монотонности и постоянства функций
- •(25)Правило Лопеталя
- •2) Необходимый признак экстремума
- •3) Достаточные признаки эктремума
- •(30) Асимптоты к графику функции.Построение графиков с использованием производных.
- •Построение графика функции с использованием производных:
(1)Понятие непрерывности функции.Свойства непрерывных функций.

Определение 1:
Функция
 называется непрерывной в точке
называется непрерывной в точке относительно множества
относительно множества ,
если
,
если
Замечание 1:
Если
в точке
 функция непрерывна, то в силу свойств
предела она однозначна, поэтому в
дальнейшем непрерывные функции будем
считать однозначными.
функция непрерывна, то в силу свойств
предела она однозначна, поэтому в
дальнейшем непрерывные функции будем
считать однозначными.
Замечание 2:
Если понятно относительно какого множества непрерывность, то это множество не указываем.




Определение 2:
Функция
 называется непрерывной в точке
называется непрерывной в точке относительно множества
относительно множества ,
если
,
если

Замечание:
В
данном случае не обязательно требовать,
чтобы
 ,
т.к. при
,
т.к. при
 выполняется автоматически.
выполняется автоматически.
Определение 3:
Функция
 называется непрерывной в точке
называется непрерывной в точке относительно
относительно
множества
 ,
если
,
если

Пусть
 ,
обозначим
,
обозначим ,тогда
,тогда
тогда
по определению 1 функция непрерывна в
точке
 относительно
относительно ,
когда
,
когда
 ,
,
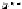

Если
функция непрерывна в каждой точке
множества
 ,
то говорят, что функция непрерывна на
множестве
,
то говорят, что функция непрерывна на
множестве
Свойства функций:
1) Общие свойства
1 св.) Пусть
 непрерывна в точке
непрерывна в точке относительно множества
относительно множества ,
, , тогда
, тогда непрерывна в точке
непрерывна в точке о тносительно множества
о тносительно множества
Доказательство:

2
св.)
 непрерывна
в точке
непрерывна
в точке относительно множества
относительно множества равносильно
непрерывности функции в точке
равносильно
непрерывности функции в точке относительно
относительно
Доказательство:
По §3.4 св. 5
3 св.) Пусть
 ,
, ,
тогда непрерывность относительно
,
тогда непрерывность относительно равносильна непрерывности в точке
равносильна непрерывности в точке как относительно
как относительно ,
так и
,
так и
Замечание:
Если точка
 в св. 3 является предельной только для
одного из множеств
в св. 3 является предельной только для
одного из множеств и
и ,
то непрерывность относительно
,
то непрерывность относительно равносильна непрерывности относительно
именно в этой точке.
равносильна непрерывности относительно
именно в этой точке.
4 св.) (предельный переход под знаком непрерывности функции)
1. Если
 непрерывна в точке
непрерывна в точке относительно
относительно ,
,
2.
 ,
,
тогда
 или
или
Следствие:
(теорема о непрерывности сложной функции)
1. Если
 непрерывна в точке
непрерывна в точке относительно множества
относительно множества ,
, ,
,
2.
 непрерывна в точке
непрерывна в точке ,
, ,
,
тогда
 непрерывна в точке
непрерывна в точке относительно множества
относительно множества
5 св.) Если
 непрерывна в точке
непрерывна в точке относительно множества
относительно множества ,
, тоже непрерывная функция в точке
тоже непрерывная функция в точке относительно множества
относительно множества
Доказательство:
По §3.7 следствие теоремы о двух милиционерах


6 св.) (непрерывность результатов арифметических действий на непрерывных функциях)
Если
 и
и непрерывны
в точке
непрерывны
в точке относительно множества
относительно множества ,
то:
,
то: непрерывны в точке
непрерывны в точке ,
относительно множества
,
относительно множества
(следует из §3.6 и определения непрерывности)
Следствие:
Многочлен и дробно-рациональные функции непрерывны во всех точках своей области определения.
Доказательство:
 непрерывна
непрерывна

 непрерывен
непрерывен
 непрерывен. Т.к. каждый многочлен –
непрерывная функция
непрерывен. Т.к. каждый многочлен –
непрерывная функция тоже непрерывна
тоже непрерывна
2) Односторонняя непрерывность
Определение:
 называется
непрерывной в точке
называется
непрерывной в точке
 относительно множества
относительно множества справа (слева), если
справа (слева), если непрерывна в точке
непрерывна в точке относительно множества
относительно множества

Теорема:
Пусть
 ,
тогда для того чтобы функция была
непрерывна в точке
,
тогда для того чтобы функция была
непрерывна в точке относительно
относительно ,
необходимо и достаточно чтобы она была
непрерывна в точке
,
необходимо и достаточно чтобы она была
непрерывна в точке и справа и слева
и справа и слева
Доказательство:
По §3.4, св. 6
3) Непрерывность монотонной и обратной к строго монотонной функции
Теорема 1:
(о непрерывности монотонной функции)
Если: 1) монотонна на
монотонна на
2) область
значений
 есть промежуток,
есть промежуток,
тогда
 непрерывна во всех точках предельной
для нее
непрерывна во всех точках предельной
для нее
Доказательство:
 ,
докажем непрерывность в точке
,
докажем непрерывность в точке
 слева и справа.
слева и справа.
Слева (справа):
Пусть
 ,
, - возрастает. По теореме о пределе
монотонной функции:
- возрастает. По теореме о пределе
монотонной функции: (1). Т.к.
(1). Т.к. возрастает
возрастает
 (2). Покажем, что в неравенстве (2) знак
«
(2). Покажем, что в неравенстве (2) знак
« »
не имеет места. Пусть
»
не имеет места. Пусть ,
тогда для
,
тогда для (а такие есть)
(а такие есть) (3) т.к. возрастает, а для
(3) т.к. возрастает, а для
 (4). Из (3),(4) следует, что функция принимает
значения
(4). Из (3),(4) следует, что функция принимает
значения и не принимает значения на промежутке
и не принимает значения на промежутке .
Это противоречит тому, что по условию
значение функции – промежуток
.
Это противоречит тому, что по условию
значение функции – промежуток в (2) меньше быть не может.
в (2) меньше быть не может.
Лемма:
Функция обратная к строго монотонной (однозначная) однозначна и строго монотонна в том же направлении.
Доказательство:
Пусть
 строго возрастает на множестве
строго возрастает на множестве .
Рассмотрим обратную к ней
.
Рассмотрим обратную к ней
 (
( - область значений
- область значений )
) точка
точка .
Т.к.
.
Т.к. строго возрастает, то
строго возрастает, то .
Возьмём
.
Возьмём из
из ,
, ,
, .
Если бы
.
Если бы ,
тогда
,
тогда - функция строго возрастает
- функция строго возрастает
Теорема 2:
(о непрерывности функции обратной к строго монотонной)
Функция обратная к строго монотонной, определённой на промежутке непрерывна во всех точках своей области определения.
Доказательство:
Функция
 определена на промежутке и строго
монотонна.
определена на промежутке и строго
монотонна. по лемме
по лемме однозначна и монотонна на
однозначна и монотонна на ,
а область значений
,
а область значений по
теореме 1
по
теореме 1 непрерывна.
непрерывна.
