
- •Алгебра
- •Гл. 1. Алгебра матриц
- •1.2 Принцип равенства
- •1.3 Транспонированная матрица
- •1.4 Сложение матриц
- •1.5 Умножение матрицы на число
- •1.6 Скалярное умножение арифметических векторов
- •1.7 Умножение матриц
- •1.8 Теория делимости квадратных матриц
- •1.9. Основные типы алгебраических структур.
- •1.10 Элементарные преобразования над матрицами и элементарные
- •1.11 Эквивалентные матрицы
- •1.12 Отношение эквивалентности.
- •1.13 Разложение матрицы в произведение простейших
- •1.14 Матричные уравнения
- •Упражнения
- •Историческая справка
- •Литература Основная литература.
- •Задачники и дополнительные методические материалы.
1.14 Матричные уравнения
Уравнение, называется матричным, если в качестве неизвестного оно содержит матрицу. Простейшие матричные уравнения имеют вид
![]() , (1.24)
, (1.24)
![]() , (1.25)
, (1.25)
![]() , (1.26)
, (1.26)
где
![]() – известные матрицы, а
– известные матрицы, а![]() – неизвестные матрицы соответствующих
размеров. В общем случае уравнения
(1.24)-(1.26) эквивалентны некоторым системам
линейных алгебраических уравнений
(СЛАУ), но в том частном случае, когда
матрицы
– неизвестные матрицы соответствующих
размеров. В общем случае уравнения
(1.24)-(1.26) эквивалентны некоторым системам
линейных алгебраических уравнений
(СЛАУ), но в том частном случае, когда
матрицы![]() и
и![]() обратимы, теория этих уравнений проста.
Прежде чем изложить её отметим, что
числовая матрица
обратимы, теория этих уравнений проста.
Прежде чем изложить её отметим, что
числовая матрица![]() является решением уравнения (1.24), если
при подстановке её в это уравнение
вместо матрицы
является решением уравнения (1.24), если
при подстановке её в это уравнение
вместо матрицы![]() мы получаем верное матричное равенство
(и аналогично для уравнений (1.25) и (1.26)).
мы получаем верное матричное равенство
(и аналогично для уравнений (1.25) и (1.26)).
Предложение
1.8. Пусть
матрицы
![]() и
и![]() обратимы, тогда уравнения(1.24)-(1.26)
разрешимы при любых правых частях
обратимы, тогда уравнения(1.24)-(1.26)
разрешимы при любых правых частях
![]() соответственно, а их единственные
решения определяются по формулам
соответственно, а их единственные
решения определяются по формулам
![]() , (
, (![]() )
)
![]() , (
, (![]() )
)
![]() , (
, (![]() )
)
◄ Так как уравнения
(1.25) и (1.26) являются частными случаями
уравнения (1.24) (![]() в первом случае и
в первом случае и![]() во втором случае), доказательство
проведём лишь для уравнения (1.24).
(Рассуждения в случае уравнений (1.25) и
(1.26) предлагаем читателю провести
самостоятельно.)
во втором случае), доказательство
проведём лишь для уравнения (1.24).
(Рассуждения в случае уравнений (1.25) и
(1.26) предлагаем читателю провести
самостоятельно.)
Пусть
![]() ,
,![]() ,
тогда по необходимости матрицы
,
тогда по необходимости матрицы![]() и
и![]() имеют размер
имеют размер![]() .
Так как
.
Так как![]() ,
,![]() ,
то для любой матрицы
,
то для любой матрицы![]() из
из![]() существует матрица
существует матрица![]() вида (
вида (![]() ).
Подставляя её в уравнение (1.24), получаем
).
Подставляя её в уравнение (1.24), получаем
![]() ,
,
т.е. матрица вида
(![]() )
является решением уравнения (1.24). Тем
самым показано, что решение уравнения
(1.24) существует.
)
является решением уравнения (1.24). Тем
самым показано, что решение уравнения
(1.24) существует.
Осталось показать
его единственность. В самом деле, пусть
![]() некоторое решение уравнения (1.24), тогда
справедливо матричное равенство
некоторое решение уравнения (1.24), тогда
справедливо матричное равенство
![]() .
.
Умножая обе части
слева на матрицу
![]() ,
а справа на матрицу
,
а справа на матрицу![]() ,
получаем, что
,
получаем, что
![]()
или
![]() .
.
т.е.
![]() имеет вид (
имеет вид (![]() ).
►
).
►
Два матричных уравнения будем называть равносильными, если они имеют одинаковые решения. В частности, если у одного из равносильных уравнений решений нет, то их нет и у второго уравнения. В последнем случае мы предполагаем, что неизвестные матрицы, входящие в оба уравнения, имеют одинаковые размеры.
Предложение
1.9. Пусть
![]() и
и![]() .
Тогда уравнения
.
Тогда уравнения
![]() , (1.27)
, (1.27)
![]() (1.28)
(1.28)
равносильны для
любых матриц
![]() из
из
![]() .
.
◄ Действительно,
если
![]() – решение уравнения (1.27), тогда
– решение уравнения (1.27), тогда![]() .
Умножая обе части этого равенства слева
на матрицу
.
Умножая обе части этого равенства слева
на матрицу![]() ,
получаем, что.
,
получаем, что.
![]() или
или
![]() ,
,
т.е.
![]() является решением уравнения (1.28).
Наоборот, если
является решением уравнения (1.28).
Наоборот, если![]() – решение уравнения (1.28), тогда
– решение уравнения (1.28), тогда
![]() .
.
Но матрица
![]() обратима. Умножая обе части последнего
равенства слева на матрицу
обратима. Умножая обе части последнего
равенства слева на матрицу![]() ,
получаем, что
,
получаем, что
![]() ,
,
т.е.
![]() – решение уравнения (1.27). Если же у одного
из уравнений (1.27) или (1.28) решений нет,
тогда их нет и у второго уравнения, так
как в противном случае, повторяя
проведённые выше рассуждения, приходим
к противоречию. ►
– решение уравнения (1.27). Если же у одного
из уравнений (1.27) или (1.28) решений нет,
тогда их нет и у второго уравнения, так
как в противном случае, повторяя
проведённые выше рассуждения, приходим
к противоречию. ►
Упражнения
1. Выяснить, какие из следующих матриц равны
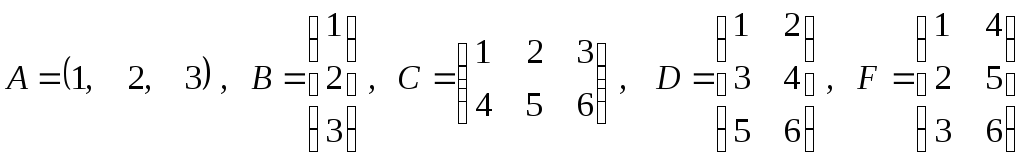 .
.
2. Написать матрицу, транспонированную данным:
 .
.
3. Если матрица
![]() имеет вид
имеет вид
 ,
,
то каков вид матрицы
![]() ?
?
4. Матрицы
![]() и
и![]() имеют вид:
имеют вид:
а)
![]() б)
б)![]() .
.
Каковы размеры
матрицы
![]() ,
если известно, что
,
если известно, что![]() ?
?
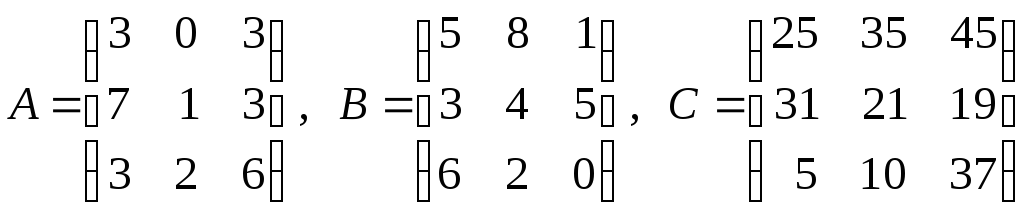
5. Даны матрицы
![]() и
и![]() .
Найти матрицы
.
Найти матрицы![]() .
.
а)
![]() ;
б)
;
б)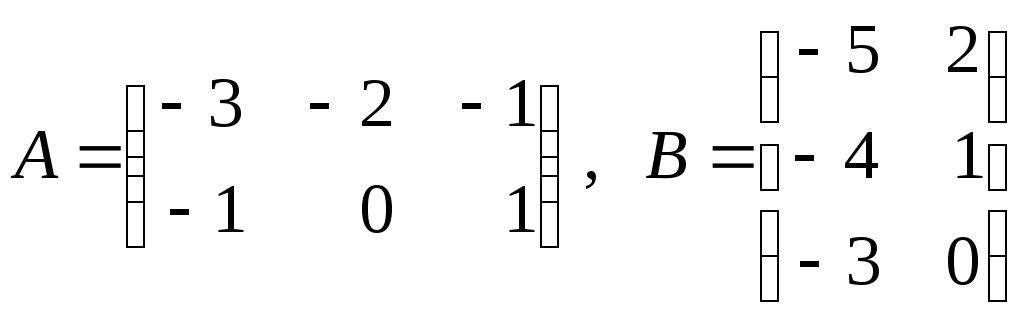 ;
;
в)
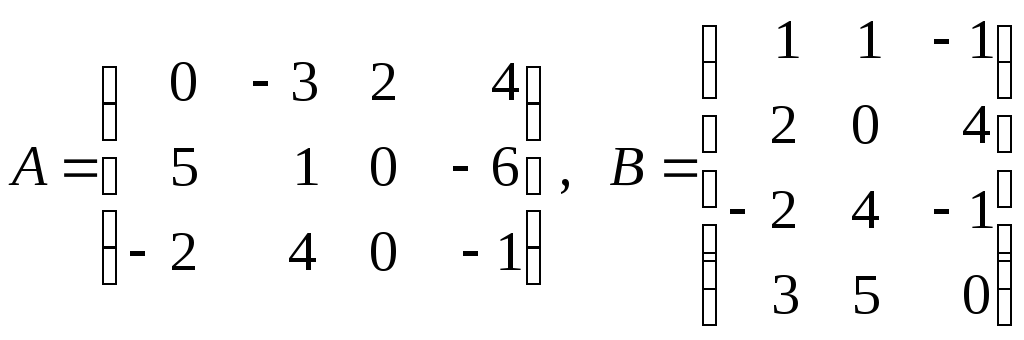 .
.
6. Найти произведение
матриц
![]() ,
если:
,
если:
а)
![]() ; б)
; б)![]() ;
;
в)
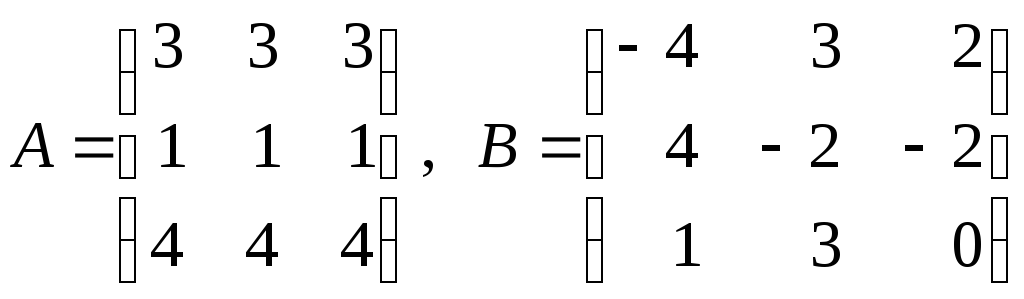 ;
г)
;
г)
д)
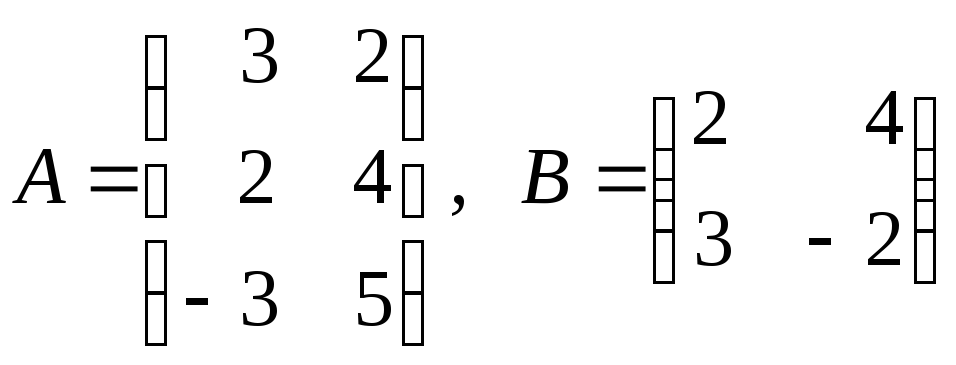 ; е)
; е) ;
;
ж)
 ;
;
з)
 ;
;
и)
![]() ;
к)
;
к)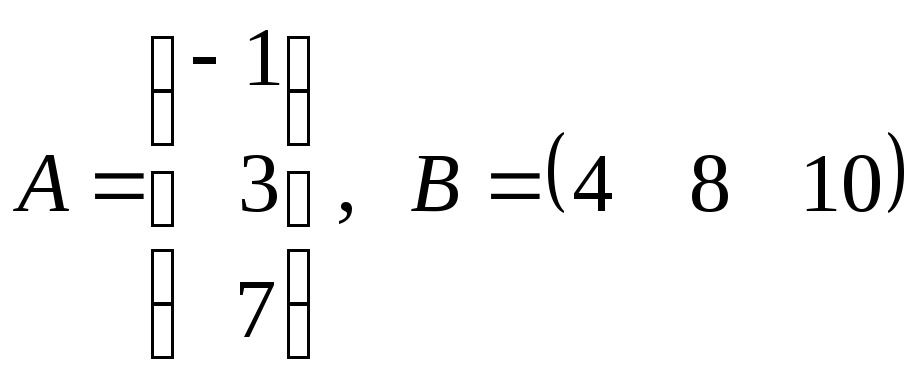 ;
;
л)
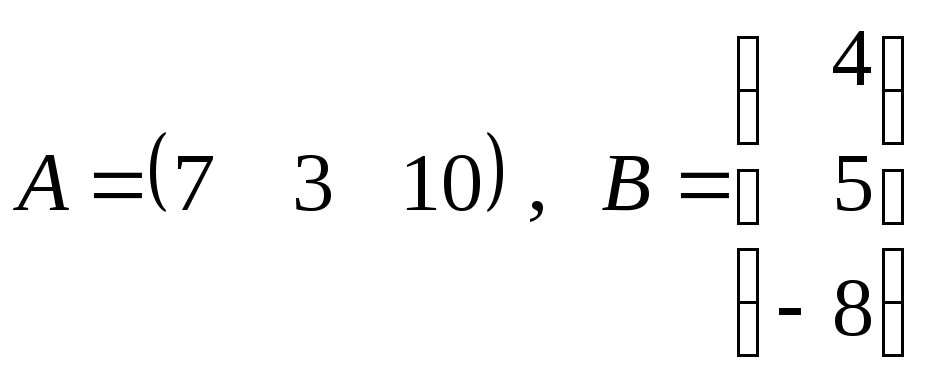 ;
м)
;
м)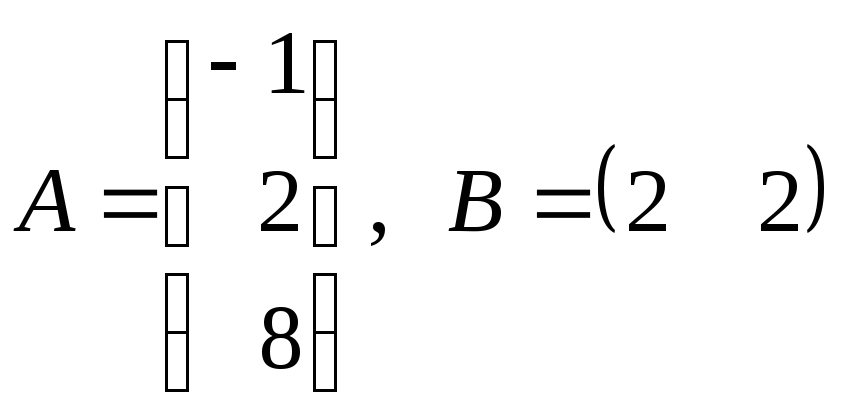 .
.
При вычислении сложных матричных выражений целесообразно продумать порядок действий, так как от этого зависит объём вычислений.
Пример
10. Найти
матрицу
![]() ,
если
,
если
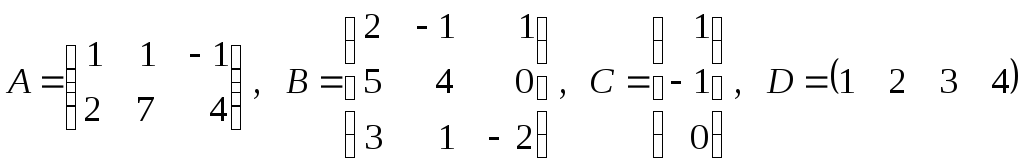 .
.
◄ Матрица
![]() существует, так как порядки сомножителей
согласованны
существует, так как порядки сомножителей
согласованны
![]() ,
,
и имеем порядок
![]() .
Благодаря свойству ассоциативности
операции умножения матриц последовательность
её вычисления может быть различной,
например,
.
Благодаря свойству ассоциативности
операции умножения матриц последовательность
её вычисления может быть различной,
например,![]() или
или![]() .
.
Напомним, что при
вычислении произведения двух матриц
используется скалярное умножение двух
арифметических векторов порядка
![]() .
Будем называть это скалярное умножение
«простым», если
.
Будем называть это скалярное умножение
«простым», если![]() ,
и – «сложным», если
,
и – «сложным», если![]() (сокращённо ПСУ и ССУ). Посчитаем
количества ПСУ и ССУ, которые необходимо
совершить, чтобы вычислить матрицу
(сокращённо ПСУ и ССУ). Посчитаем
количества ПСУ и ССУ, которые необходимо
совершить, чтобы вычислить матрицу![]() указанными выше способами.
указанными выше способами.
В первом случае последовательность вычислений такова:
1)![]() – 6
ССУ
– 6
ССУ
![]()
2)
![]() – 2
ССУ
– 2
ССУ
![]()
3)
![]() – 8
ПСУ.
– 8
ПСУ.
![]()
Всего: 8 ССУ и 8 ПСУ.
Во втором случае:
1)![]() – 12
ПСУ
– 12
ПСУ
![]()
2)![]() – 12
ССУ
– 12
ССУ
![]()
3)
![]() – 8
ССУ.
– 8
ССУ.
![]()
Всего: 20 ССУ и 12 ПСУ.
Преимущество
первого способа над вторым очевидно.
Но есть ещё один порядок умножения,
позволяющий сократить объём вычислений.
Именно,
![]() .
.
В самом деле,
1)![]() – 3
ССУ
– 3
ССУ
![]()
2)
![]() – 2
ССУ
– 2
ССУ
![]()
3)
![]() – 8
ПСУ.
– 8
ПСУ.
![]()
Всего: 5 ССУ и 8 ПСУ.
Анализ трёх
рассмотренных способов вычисления
матрицы
![]() позволяет дать рекомендацию: при
вычислении матричных произведений с
числом сомножителей больше 2-х целесообразно
начинать вычисление произведений с
наименьшим числом столбцов у правого
сомножителя, и заканчивать вычислением
произведений с наибольшим числом
столбцов у правого сомножителя. ►
позволяет дать рекомендацию: при
вычислении матричных произведений с
числом сомножителей больше 2-х целесообразно
начинать вычисление произведений с
наименьшим числом столбцов у правого
сомножителя, и заканчивать вычислением
произведений с наибольшим числом
столбцов у правого сомножителя. ►
7. Найти произведение
![]() ,
если:
,
если:
а)
![]() ;
;
б)
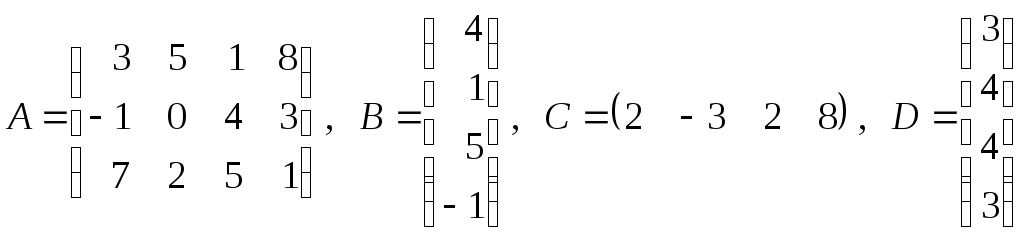 ;
;
в)
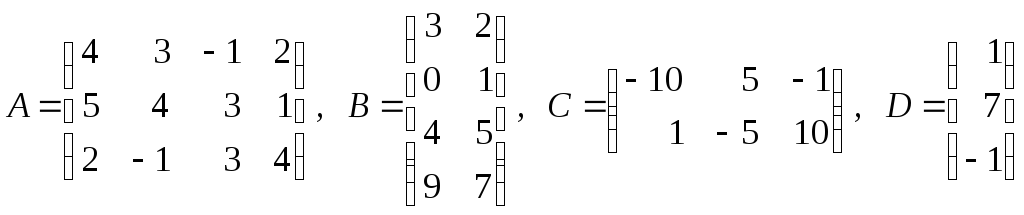 ;
;
г)
 .
.
При вычислении
матричных выражений вида
![]() предварительно следует привести подобные
члены, если это возможно.
предварительно следует привести подобные
члены, если это возможно.
Пример 11. Найти матрицу
![]() ,
,
если
![]() ,
,
![]() .
.
◄ Приводим подобные
члены в исходном выражении для матрицы
![]() ,
,
![]() .
.
Так как
![]() ,
,
![]() .
►
.
►
8. Найти матрицу
![]() ,
если:
,
если:
а)
![]()
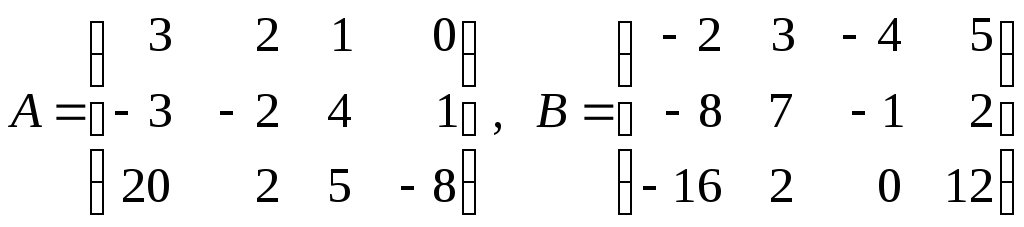 ;
;
б)
![]()
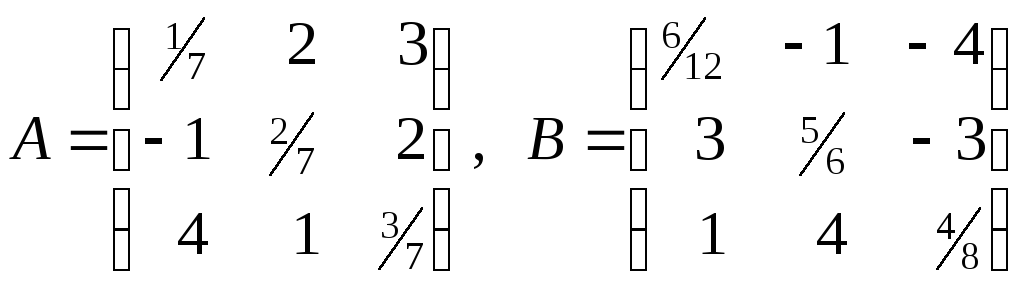 .
.
Часто сложное матричное выражение можно до его вычисления привести к более простому виду, используя свойства операций над матрицами.
Пример 12. Найти матрицу
![]() ,
,
если
![]()
◄ Заметив, что
![]() ,
,
где
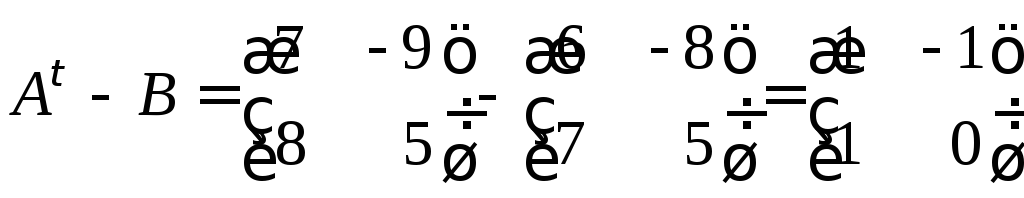 ,
,
получаем, что
 .
►
.
►
9. Найти матрицу
![]() ,
если:
,
если:
а)
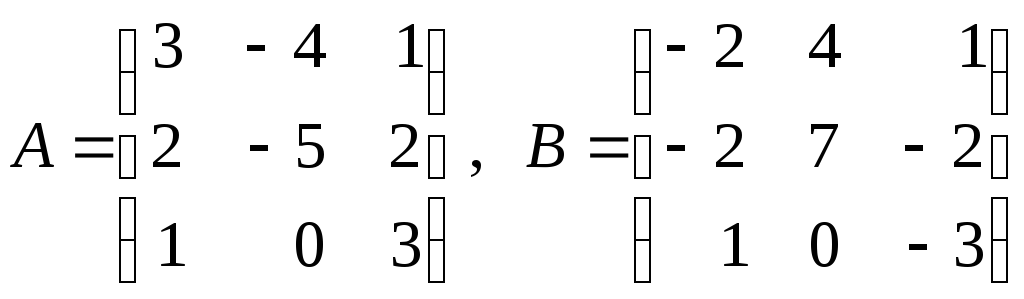 ;
;
б)
![]() .
.
10. Найти матрицу
![]() ,
если:
,
если:
а)
![]() ;
;
б)
![]() ;
;
в)
 .
.
11. Найти матрицу
![]() ,
если
,
если
 .
.
12. Найти матрицу
![]() ,
если:
,
если:
а)
![]() ;
;
б)
 .
.
Введём обозначение для степени матрицы
![]() ,
,
И заметим, что ввиду некоммутативности операции умножения матриц
![]() .
.
Из
условия согласования следует, что
степень матрицы определена только для
квадратных матриц, а степень произведения
![]() определена для матриц прямоугольного
вида. При этом число строк матрицы
определена для матриц прямоугольного
вида. При этом число строк матрицы![]() должно совпадать с числом столбцов
матрицы
должно совпадать с числом столбцов
матрицы![]() .
.
При вычислении
степеней матриц и матричных выражений
следует попытаться среди малых степеней
![]() найти максимально простую матрицу с
тем, чтобы использовать её для упрощения
вычисления матрицы
найти максимально простую матрицу с
тем, чтобы использовать её для упрощения
вычисления матрицы![]() .
.
Пример 13. а) Найти матрицу
![]() .
.
◄ Пусть
![]() ,
тогда
,
тогда
Поэтому
![]()
 ►
►
б) Найти матрицу
![]() ,
где
,
где
![]() .
.
◄ Рассмотрим
матрицы
![]() и
и![]() :
:
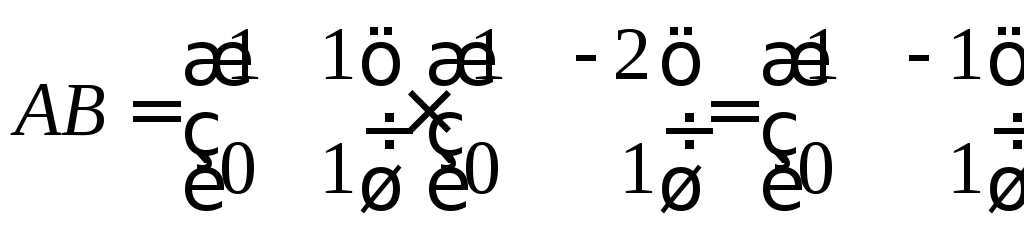 ,
,
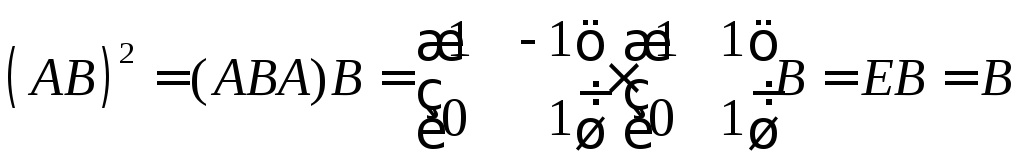 .
.
Но тогда
![]() .
►
.
►
13. Вычислить значение матричного выражения:
а)
![]() ,
если
,
если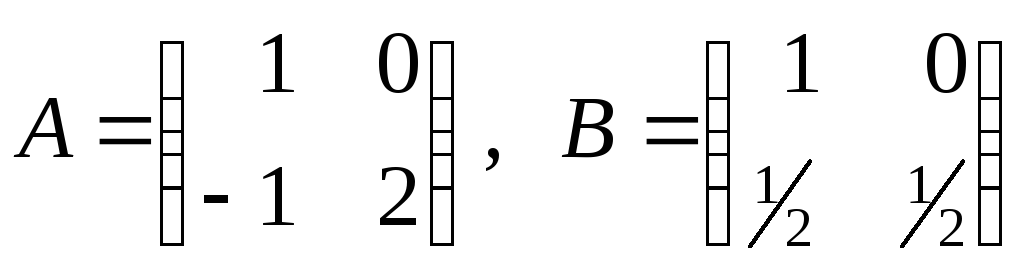 ;
;
б)
![]() ,
если
,
если ;
;
в)
![]() ,
если
,
если
 ,
,
 .
.
14. Вычислить
 .
.
Пусть
![]() – многочлен,
– многочлен,![]() ,
,![]() ,
,![]() .
Многочленом
.
Многочленом![]() от матрицы
от матрицы![]() называется матричное выражение
называется матричное выражение
![]() ,
где
,
где
![]() .
.
Пример
14. Найти
значение
![]() ,
если
,
если
![]() .
.
◄ По определению
![]()
![]() .
►
.
►
15. Найти значение
![]() :
:
а)
![]() ;
;
б)
 ;
;
в)
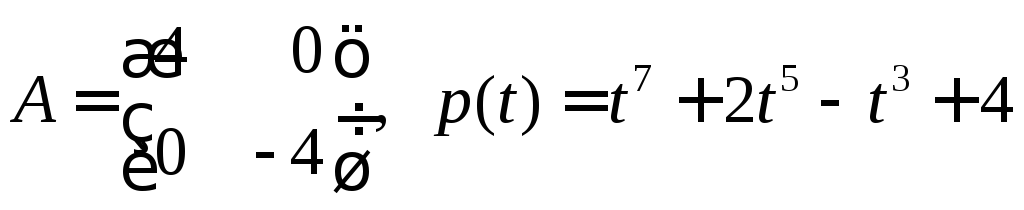 .
.
Аппарат элементарных матриц позволяет находить обратную матрицу, если исходная матрица обратима.
Пример
15. Разложить
матрицу
![]() в произведение простейших. Выяснить,
является ли матрица
в произведение простейших. Выяснить,
является ли матрица![]() обратимой, и в случае её обратимости
найти матрицу
обратимой, и в случае её обратимости
найти матрицу![]() ,
если
,
если
![]() .
.
◄ Решение основано
на предложении 1.6 (см. пример 9). Приводим
элементарными преобразованиями матрицу
![]() к виду
к виду![]() ,
,
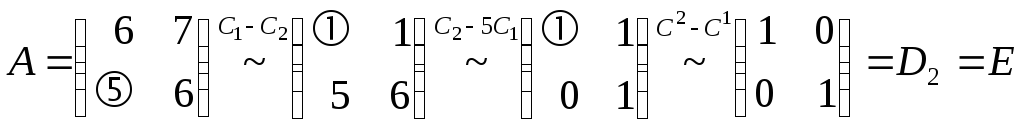 .
.
Матрица
![]() обратима и удовлетворяет соотношению
обратима и удовлетворяет соотношению
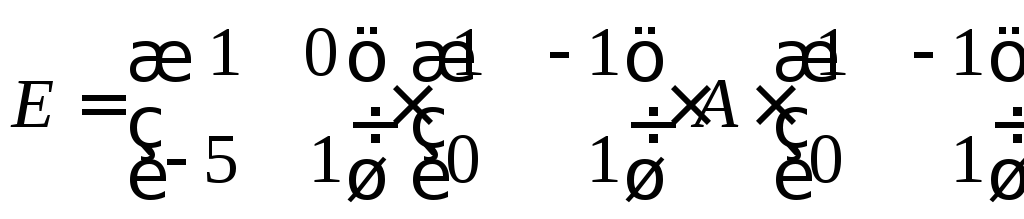 .
.
Умножая полученное равенство справа на матрицу
![]() ,
,
получаем, что
 .
.
Теперь умножаем новое равенство на матрицу
![]()
слева,
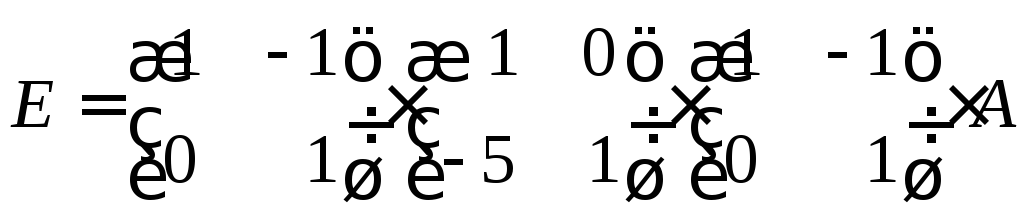 .
.
Матрица
![]() обратима и
обратима и![]() .
Поэтому
.
Поэтому
![]() ).
).
Откуда следует что
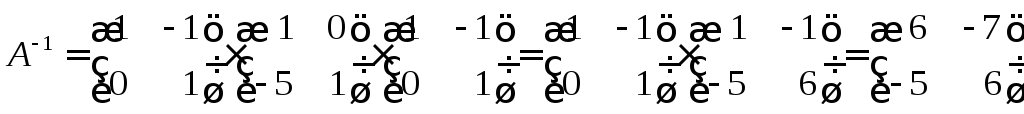 .
►
.
►
16. Указать
элементарные матрицы, отвечающие
следующим элементарным преобразованиям
матрицы размера
![]() :
:
![]() .
.
17. Каким элементарным
преобразованиям матрицы размера
![]() соответствуют элементарные матрицы:
соответствуют элементарные матрицы:
 ,
,  ,
, ,
,
 ,
,  ,
, .
.
18. В матрице
![]() произвести элементарные преобразования
умножением на соответствующие элементарные
матрицы
произвести элементарные преобразования
умножением на соответствующие элементарные
матрицы![]() или
или![]() (
(![]() соответствуют строчным преобразованиям,
соответствуют строчным преобразованиям,![]() – столбцовым):
– столбцовым):
а)
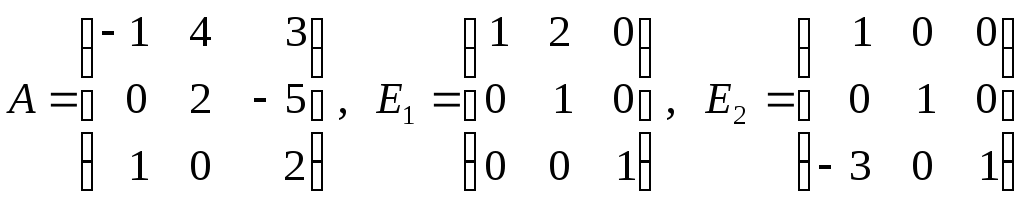 ,
,
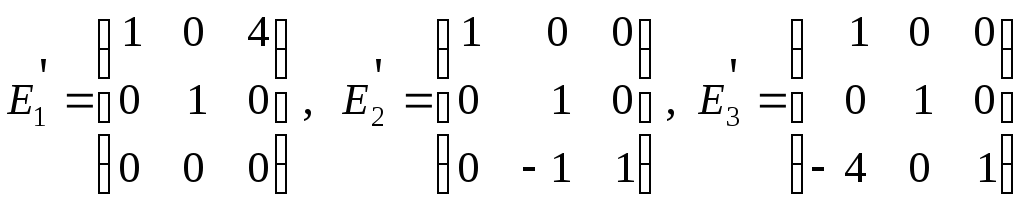 .
.
б)
 ,
,
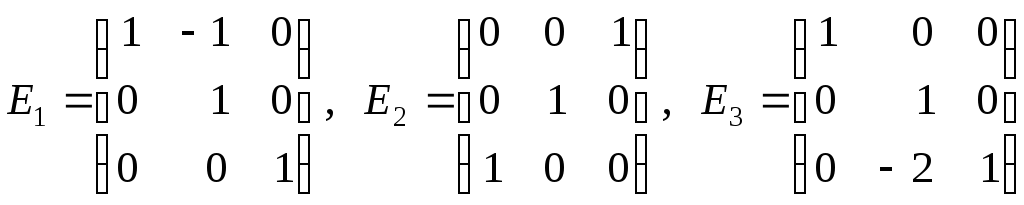 ,
,
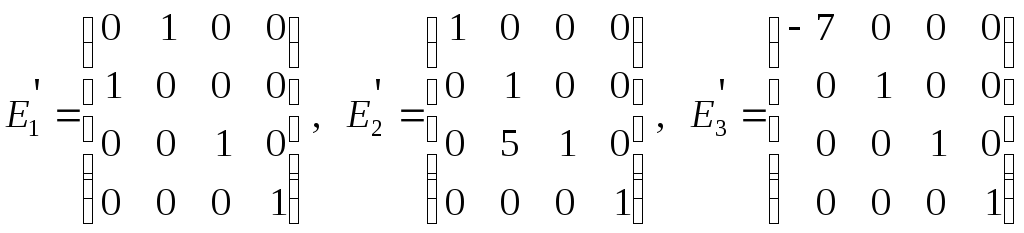 .
.
19. Элементарными
преобразованиями привести матрицу к
виду
![]() :
:
а)
 ,
б)
,
б)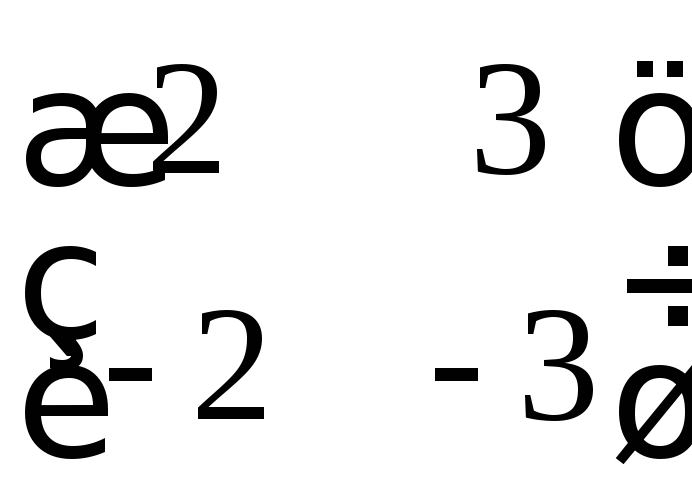 ,
в)
,
в) , г)
, г) ,
,
д)
![]() ,
е)
,
е)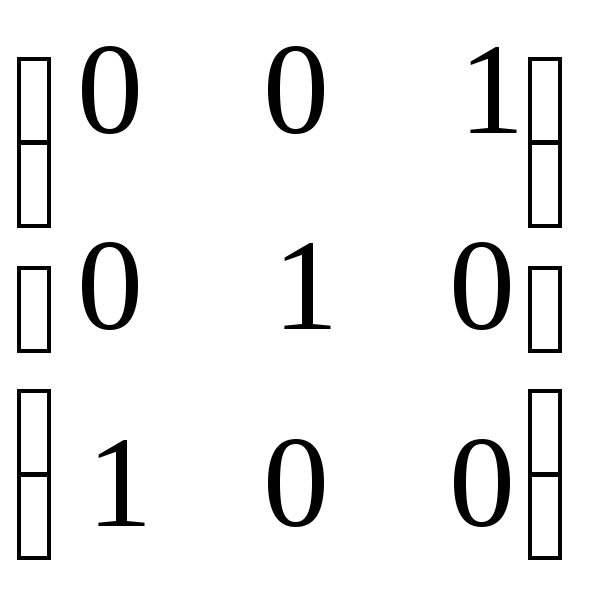 ,
ж)
,
ж)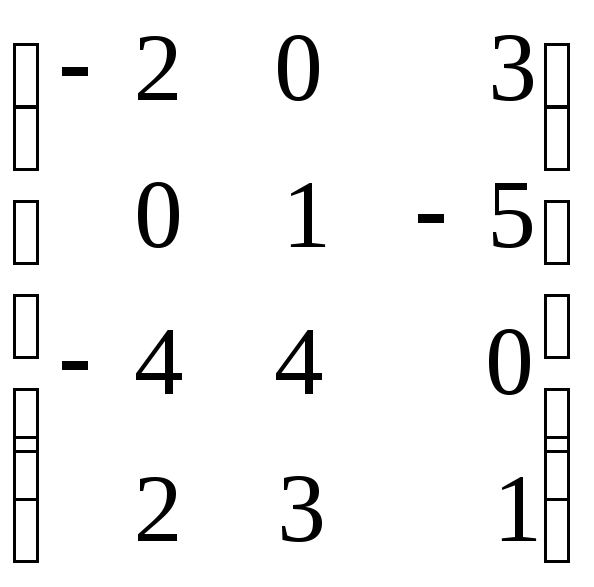 ,
з)
,
з) .
.
20. Матрицы из упражнения 19 разложить в произведение простейших.
21.
Выяснить, является ли матрица
![]() обратимой, и в случае её обратимости
найти матрицу
обратимой, и в случае её обратимости
найти матрицу![]() .
Матрица
.
Матрица![]() имеет вид:
имеет вид:
а)
![]() , б)
, б)![]() , в)
, в) .
.
Замечание. В следующей главе, основываясь на данном методе обращения матриц, мы построим более эффективную вычислительную схему для нахождения обратной матрицы, связанную с методом Гаусса решения систем линейных алгебраических уравнений.
