1.12 Отношение эквивалентности.

Пусть – непустое множество произвольной природы и– его декартов квадрат.Бинарным отношением на множестве называется произвольное непустое подмножествов. бинарное отношение на множествеможно определить указанием всех пар, принадлежащих, говоря при этом, что элементыииз множестванаходятся в отношении . Поскольку это не всегда удобно (например, если множество бесконечно), то высказывание “” заменяется специальными высказываниями, зависящими от контекста, например,

.

которые читаются соответственно как “ больше ”, “ равно ”, “ влечёт ”, “ эквивалентно ”

Бинарное отношение на множественазываетсяотношением эквивалентности на множестве , если оно удовлетворяет условиям:

1) для любого,

2) если , тогда,

3) если и, тогда.

Для отношения эквивалентности принято обозначение . Условия 1)‑3), называемые аксиомами отношения эквивалентности, в этом обозначении выглядят так:

1’) , (рефлексивность)

2’) , (симметричность)

3’) и. (транзитивность)

Введение на множестве какого-нибудь отношения эквивалентности приводит к разбиению множества наклассы эквивалентности, то есть к представлению этого множества в виде объединения конечного или бесконечного числа попарно непересекающихся подмножеств эквивалентных между собой элементов. Множество классов эквивалентности при этом называется фактор-множеством множества по бинарному отношениюи обозначается. Построение фактор-множества множествапо какому-нибудь отношению эквивалентности называетсяфакторизацией множества . Задача факторизации множества является математической формализацией проблемы классификации объектов, с которой мы сталкиваемся не только в любой научной области, будь то физика (элементарные частицы), химия (таблица Менделеева), медицина (вирусология), лингвистика (части речи) или геология (классификация топов пород), но и в повседневной жизни (проблемы прописки, гражданства или деления Думы на фракции).

В алгебре матриц отношения “л‑эквивалентности”, “п‑эквивалентности” и “эквивалентности”, введенные в предыдущем пункте, являются отношениями эквивалентности на множестве . Наиболее важным из них является последнее отношение, которое приводит к построению фактор-множества, в одном классе эквивалентности которого содержатся те и только те матрицы, которые строчными и столбцовыми элементарными преобразованиями приводятся к матрицевида (1.21) с данным. Нетрудно посчитать, что различных видов матрицвсего. Это отношение эквивалентности в алгебре называется “одинаковый ранг” и подробно будет изучено во второй части нашего курса.

Предлагаем читателю самостоятельно рассмотреть фактор-множества по двум другим указанным выше отношениям эквивалентности при различных соотношениях междуи.

Лекция V.

План

1.13 Разложение матрицы в произведение простейших

1.14 Матричные уравнения

1.13 Разложение матрицы в произведение простейших

Пусть – некоторые матрицы. Введём следующее обозначение, предполагая при этом, что произведение в правой части существует,

.

Предложение 1.5. Любую ненулевую матрицу из можно представить в виде произведения

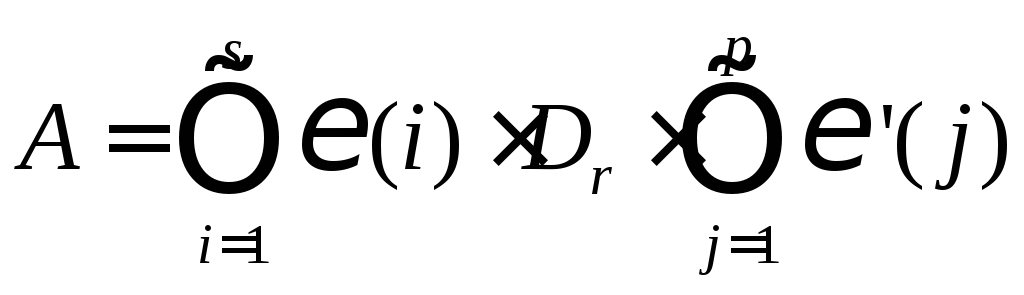, (1.22)

где , –элементарные матрицы порядка , –элементарные матрицы порядка , и матрицаимеет вид(1.21).

◄ В силу предложения 1.4 существует конечное число строчных и столбцовых элементарных преобразований, приводящих матрицу к виду. Так как проведение одного строчного элементарного преобразования в матрицеравносильно умножению этой матрицы слева на некоторую элементарнуюматрицу порядка, а проведение водного столбцового элементарного преобразования равносильно умножению матрицысправа на некоторую элементарную матрицупорядка, получаем матричное равенство

. (1.23)

Матрицы обратимы, а обратные им матрицы являются элементарными матрицами того же порядка. Поэтому, вводя обозначения

,

,

и умножая обе части равенства (1.23) в соответствующем порядке на матрицы слева и на матрицысправа, получаем

,

т.е. равенство (1.22). ►

Пример 8. разложить матрицу

в произведение простейших.

◄ Элементарными преобразованиями приводим матрицу к виду,

.

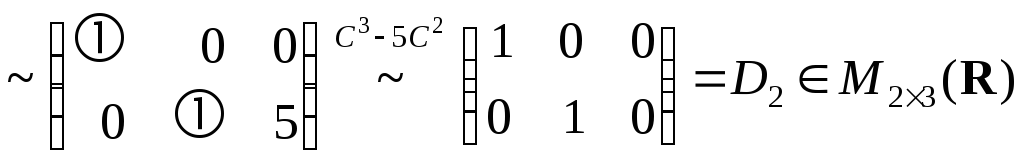Проводим эквивалентную цепочку элементарных преобразований, умножая матрицу слева на элементарную матрицу порядка 2, отвечающую элементарному преобразованию, и умножая её справа на элементарные матрицы порядка 3, отвечающие элементарным преобразованиям,,,. В результате получаем, что

.

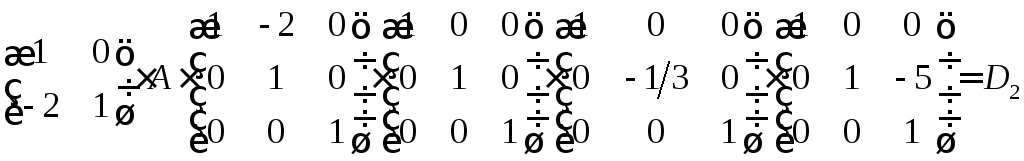Определяя обратные элементарные матрицы (см. свойство 4 элементарных преобразований) и умножая на них в соответствующем порядке последнее равенство, получаем, что

. ►

Следствием предложения 1.5 является критерий обратимости квадратной матрицы.

Предложение 1.6. (1-й критерий обратимости матрицы). Для того, чтобы матрица была обратимой, необходимо и достаточно, чтобы она была представима в виде произведения элементарных матриц.

◄ Достаточность. Элементарные матрицы обратимы, а произведение обратимых матриц есть матрица обратимая. Поэтому утверждение “матрица, представимая в виде произведения элементарных матриц, обратима” очевидно.

Необходимость. Пусть матрица обратима. Покажем, что она представима в виде произведения элементарных матриц. Прежде всего заметим, что в силу предложения 1.5 справедливо равенство (1.22), где все матрицы, входящие в это равенство, квадратные и имеют одинаковый порядок, например,. Наше утверждение будет верно, если мы покажем, что. В самом деле, матрицы

обратимы как произведение обратимых матриц. Поэтому обратимы матрицы и. Из равенства (1.22) получаем, что матрица

и является обратимой как произведение трёх обратимых матриц. Однако, матрица обратима в том и только том случае, когда. Действительно,и поэтому обратима. Если же, то матрицане может быть обратимой, так как последняя строка матрицыв этом случае нулевая и поэтому последняя строка произведениянулевая для любой матрицы, т.е. равенствоне может выполняться ни для каких матриц. В результате получаем, что матрицав данном случае имеет вид

. ►

Пример 9. Выяснить, является ли следующая матрица обратимой

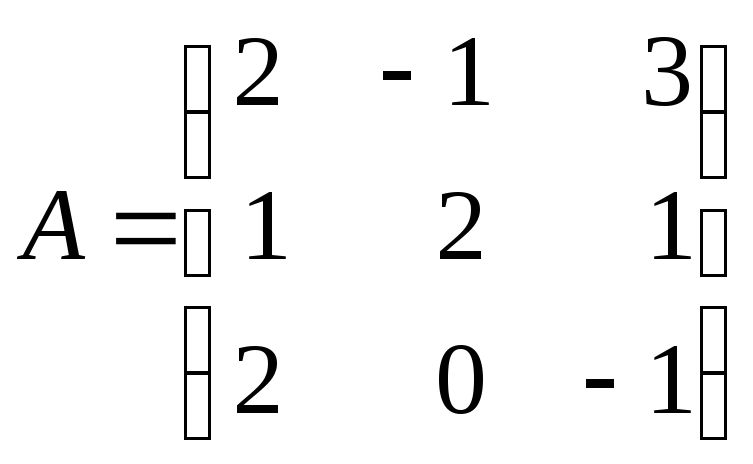
◄ Приводим матрицу к виду,

,

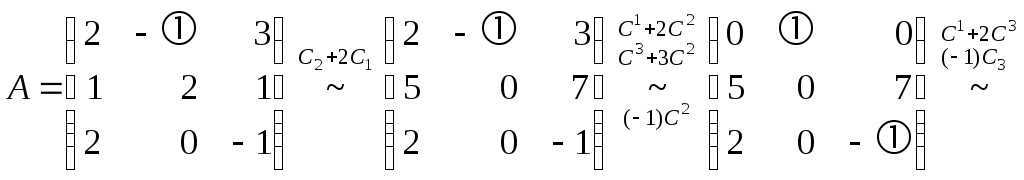
т.е. матрица обратима. Действуя дальше так же, как и в примере 6, можно представить матрицув виде произведения элементарных матриц, а после этого найти обратную матрицу. Однако этот способ обращения матриц является слишком громоздким. Ниже в Гл.2 мы разберём более простой алгоритм отыскания обратной матрицы. ►

Вернёмся к предложению 1.2. Это предложение является следствием предложений 1.5 и 1.6. В самом деле, нам нужно показать, что любая ненулевая и необратимая матрица из,, является истинным делителем нуля.

◄ Пусть и. В силу предложений 1.5 и 1.6, где. Введём матрицы

и отметим, что . Так как, то

,

. ►

В заключение этого пункта предлагаем читателю самостоятельно доказать следующее усиление предложения 1.6.

Предложение 1.7. Пусть . Следующие утверждения равносильны:

1) ;

2) ,где –элементарная матрица порядка ;

3) ;

4) ;

5) .