1.5 Умножение матрицы на число

Пусть матрица имеет вид (1.1),. Произведением матрицына числоназывается матрица

.

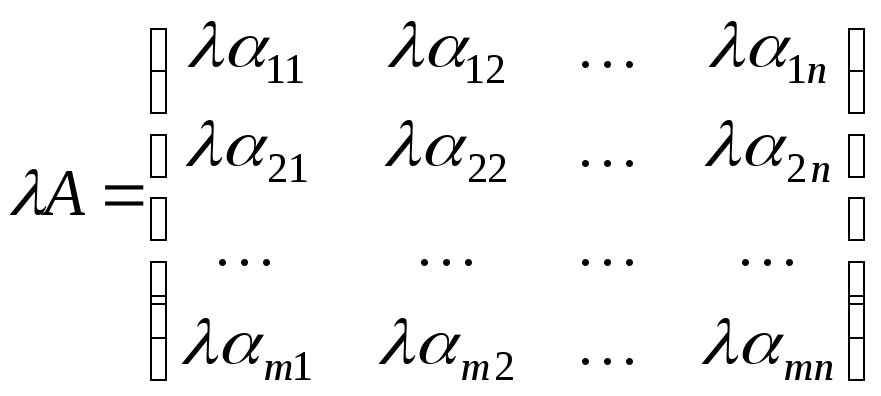Иначе говоря, умножение матрицы на число осуществляется поэлементно:

.

Отметим основные свойства введённой операции:

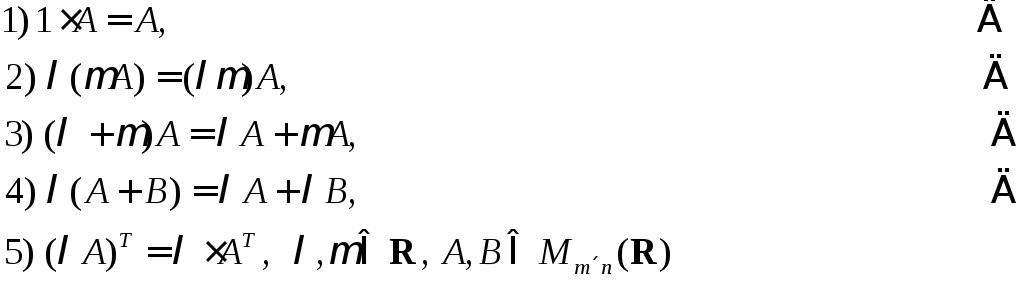
◄Действительно,

. ►

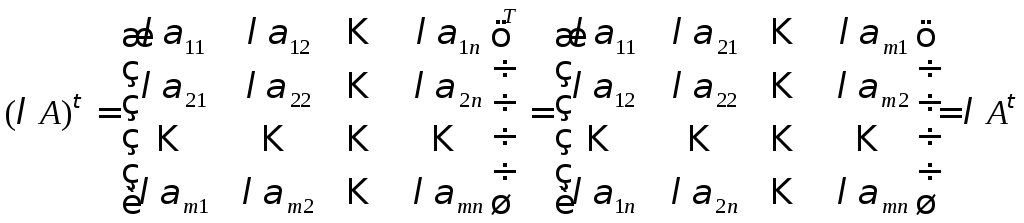Заметим также, что противоположная матрица .

Лекция II.

План

1.6 Скалярное умножение арифметических векторов

1.7 Умножение матриц

1.6 Скалярное умножение арифметических векторов

Пусть

два арифметических вектора порядка .Скалярным произведением этих векторов называется действительное число, которое обозначается и находится по правилу

(1.7)

В дальнейшем будем также считать, что скалярное произведение двух векторов-строк порядка также вводится по формуле (1.7), т.е.

.

Рассмотрим основные свойства скалярного умножения арифметических векторов.

1) Скалярное произведение симметрично, т.е.для любых и из .

◄ Действительно,

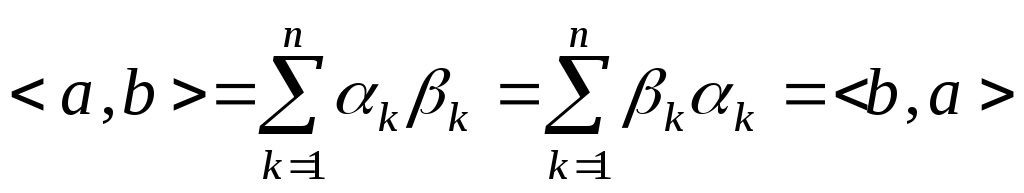
ввиду коммутативности операций умножения в . ►

2) Скалярное произведение аддитивно по каждому из сомножителей, т.е.

для любых из .

◄ Ввиду предыдущего свойства в доказательстве нуждается лишь одно из приведенных равенств. Покажем, например, справедливость первого равенства, где

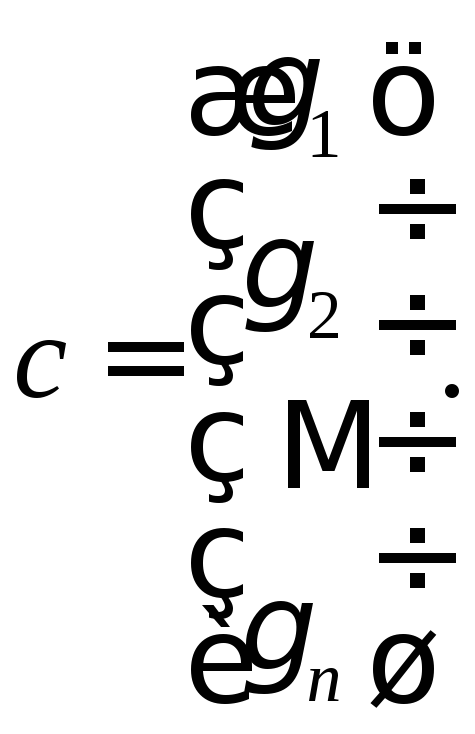
Действительно,

. ►

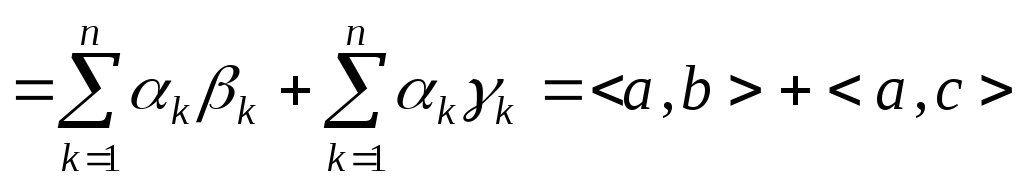3) Скалярное произведение однородно по каждому из сомножителей, т.е.

для любых действительных чисел и любых векторов и из .

Арифметический вектор являетсялинейной комбинацией векторов , если найдутся такие действительные числа, что

. (1.8)

Из свойств 2) и 3) скалярного произведения следует, что если вектор имеет вид (1.8), тогда

для любых векторов изи любых действительных чисел. Это свойство называется свойствомлинейности скалярного произведения по первому сомножителю. Аналогично имеет место свойство линейности скалярного произведения по второму сомножителю. В частности, если наряду с равенством (1.8) справедливо равенство

, где , тогда

.

4) Скалярное произведение векторана себя называетсяскалярным квадратом вектора. Скалярный квадрат любого арифметического вектора есть число неотрицательное, т.е. . Причём равенствовыполняется лишь для.

1.7 Умножение матриц

Пусть . Для того чтобы, существовало произведениенеобходимо выполнение условия согласования, т.е. число столбцов матрицыдолжно совпадать с числом строк матрицы(или порядок строк матрицыдолжен совпадать с порядком столбцов матрицы). Если условие согласования выполнено, т.е.

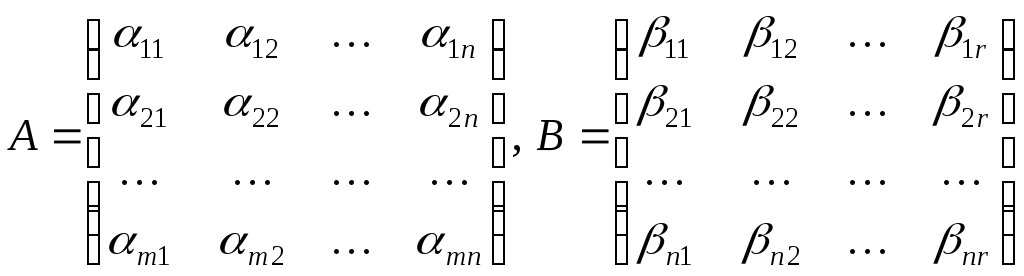
тогда произведение определено формулой

,

т.е. если , тогда

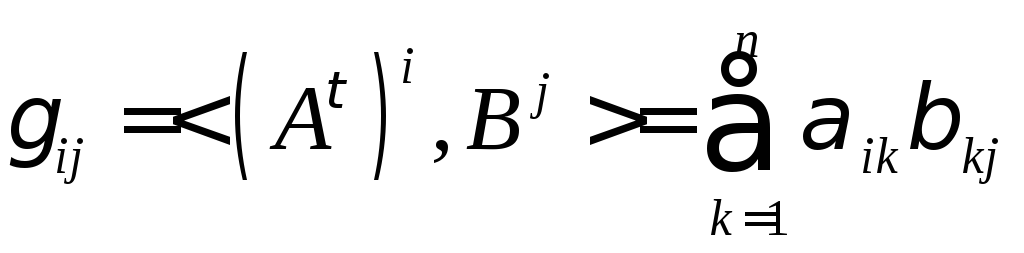
– элемент, стоящий в -ой строке и-ом столбце матрицыравен скалярному произведению-ого столбца матрицы(или транспонированной-ой строки матрицы) на-ый столбец матрицы.

Пример 2. Пусть

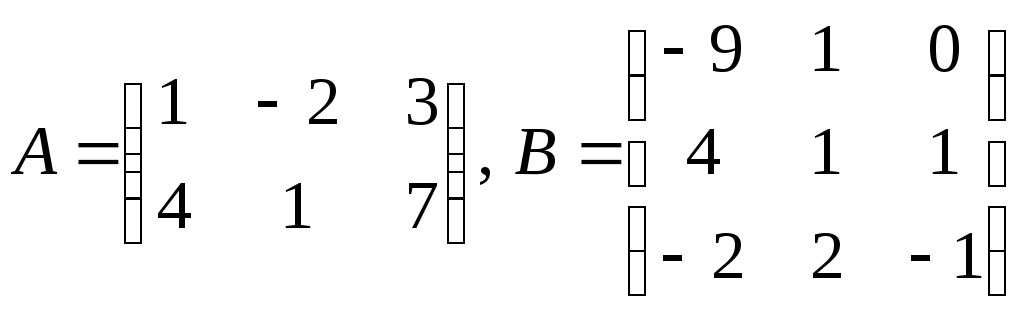
Так как , то условие согласования для матрицывыполнено и

.

Отметим также, что произведение в данном случае не существует, так как для него не выполнено условие согласования.

Заметим, что существуют и другие способы умножения матриц, естественно, приводящие к другим результатам. Данный способ умножения матриц диктуется потребностями линейной алгебры и связан с произведением (композицией, суперпозицией) так называемых линейных преобразований. Всякое линейное преобразование определяется некоторой матрицей. Во второй части курса будет показано, что матрица произведения двух линейных преобразований равна произведению матриц этих преобразований в смысле введенного выше определения.

Рассмотрим основные свойства умножения матриц.

1) Если ,тогда .

◄ Это свойство вытекает из определения произведения матриц. ►

2) Умножение матриц, вообще говоря, некоммутативно, т.е. .

◄ Прежде всего заметим, что произведение ине всегда существуют одновременно, как это видно из примера 2. Еслиисуществуют одновременно, т.е., тогда,, т.е. приматрицыиразного порядка и, следовательно, несравнимы. Но даже еслии, следовательно,иодного порядка, равенство, вообще говоря, не выполняется. Например,

. ►

В то же время существуют матрицы идля которых. Такие матрицы называютсяперестановочными. Например, матрицы

перестановочны, т.к.

.

Более того, существуют квадратные матрицы порядка , которые перестановочны со всеми матрицами из.

Примером такой матрицы во множестве является матрица

,

в чем предлагаем читателю убедиться самостоятельно.

3) Умножение матриц ассоциативно, т.е.

. (1.9)

Равенство (1.9) следует понимать так: если его левая (или правая) часть существует, тогда существует и правая (левая) часть и обе они совпадают.

Доказательство этого свойства содержится в учебнике [1], §13.

4) Умножение матриц дистрибутивно относительно сложения, т.е.

,

◄ Пусть . Тогда

. ►

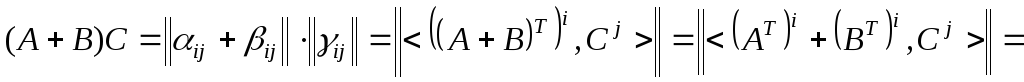
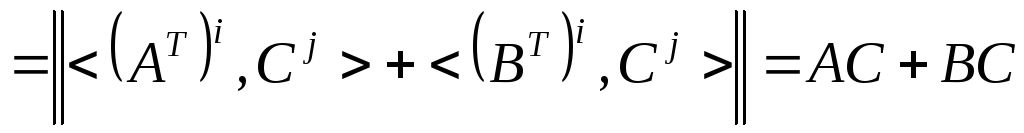5) Произведение матриц однородно по каждому из сомножителей, т.е.

, где .

◄ Например,

.

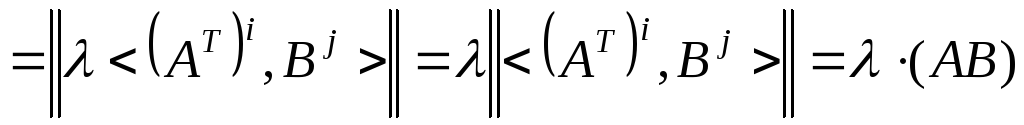Равенство доказывается аналогично. ►

6) Реакция произведения матриц на операцию транспонирования выражается формулой

(1.10)

◄ Пусть , тогда,, т.е. левая и правая части равенства (1.10) существуют и имеют одинаковые порядки. Далее

. ►

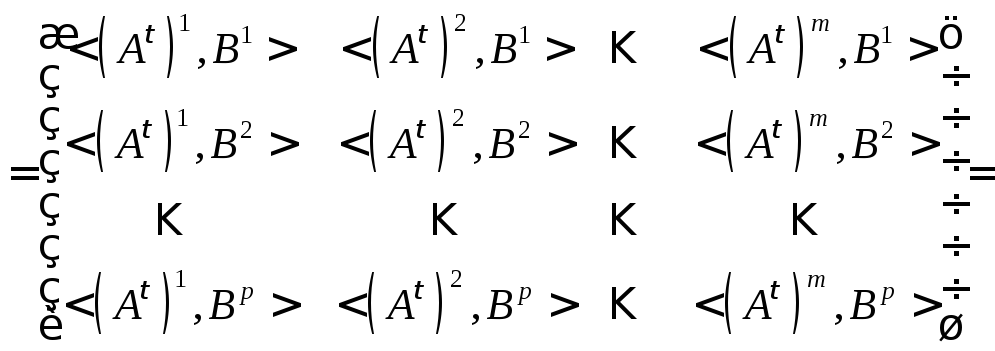
7) Рассмотрим множество квадратных матриц следующего вида:

.

Матрица называетсяединичной матрицей порядка .

Если , тогда матрицаявляется еёлевой единицей, а матрица –правой единицей, т.е.

.

Если матрица квадратная и имеет порядок, тогда матрицаявляется еёдвусторонней (левой и правой) единицей, т.е.

.

8) Напомним, что для всех действительных чисел , т.е. ноль является делителем нуля. В то же время произведениедействительных чисел может равняться нулю лишь в том случае, когда по крайней мере одно из чиселилиравно нулю. Иными словами, среди действительных чисел отсутствуют истинные (т.е. отличные от 0) делители нуля. В отличие от действительных чисел среди действительных матриц истинные делителисуществуют, т.е. найдутся такие ненулевые матрицыпорядкаипорядка, что.

◄ В самом деле, матрицы

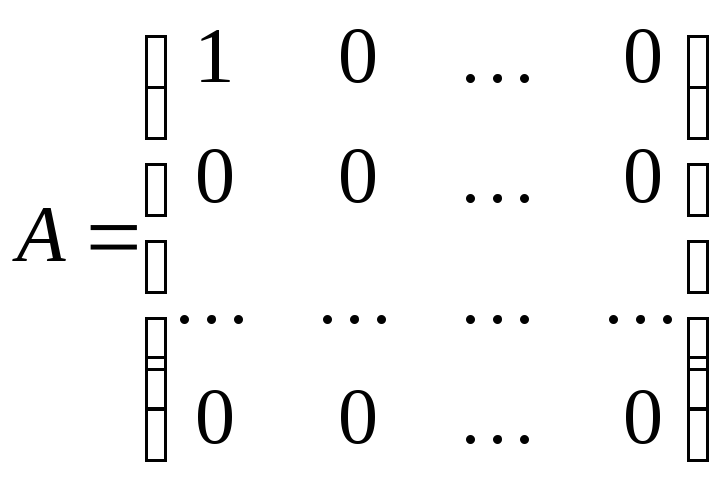и ,

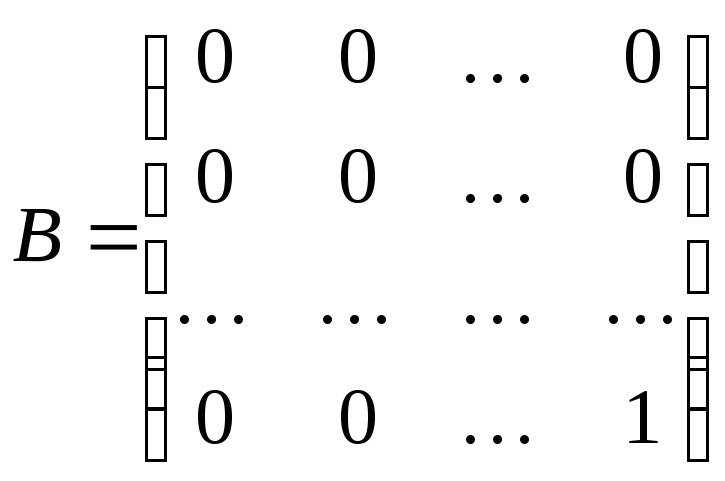соответственно порядков и, очевидно удовлетворяют нужному условию. В частности, если, то. ►

Лекция III.

План

1.8 Теория делимости квадратных матриц

1.9^* Основные типы алгебраических структур

1.10 Элементарные преобразования над матрицами

и элементарные матрицы