1.11 Эквивалентные матрицы

Нашей ближайшей целью является доказательство того, что любая матрица с помощью элементарных преобразований может быть приведена к некоторым стандартным видам. На этом пути полезным является язык эквивалентных матриц.

Пусть . Будем говорить, что матрицал‑эквивалентна (п‑эквивалентна или эквивалентна) матрице и обозначать(или), если матрицаможет быть получена из матрицыс помощью конечного числа строчных (соответственно столбцовых или строчных и столбцовых) элементарных преобразований. Ясно, что л‑эквивалентные и п‑эквивалентные матрицы являются эквивалентными.

Вначале мы покажем, что любая матрица только лишь строчными преобразованиями может быть приведена к специальному виду, называемому приведённым.

Пусть . Говорят, что ненулевая строкаэтой матрицы имеетприведённый вид, если в ней найдется такой равный 1 элемент , что все элементы столбца, отличные от, равны нулю,. Отмеченный единичный элементстрокибудем называтьведущим элементом этой строки и заключать его в кружок. Иными словами, строка матрицыимеет приведенный вид, если в этой матрице найдется столбецвида

.

Например, в следующей матрице

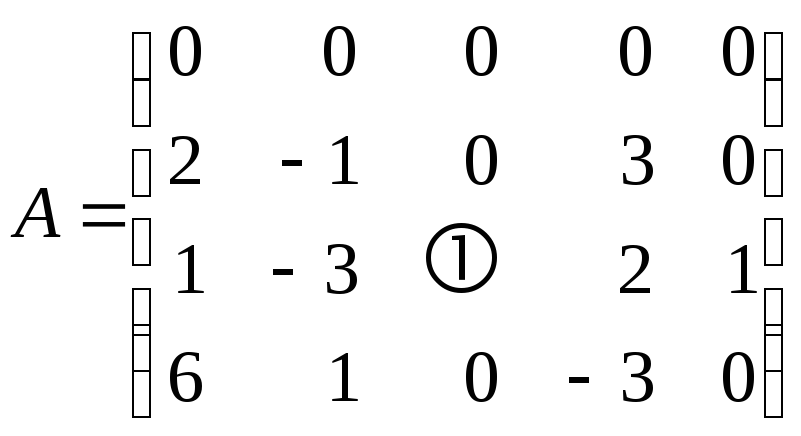
строка имеет приведенный вид, так как. Обратим внимание на то, что в этом примере на роль ведущего элемента строкипретендует также элемент. В дальнейшем, если в строке приведённого вида есть несколько элементов, обладающих свойствами ведущего, будем выделять лишь один из них произвольным образом.

Говорят, что матрица имеет приведённый вид, если каждая её ненулевая строка имеет приведённый вид. Например, матрица

имеет приведённый вид.

Предложение 1.3 Для любой матрицы существует л‑эквивалентная ей матрица приведённого вида.

◄ Во-первых, любую ненулевую строку матрицы , с помощью строчных элементарных преобразований можно сделать приведённой, т.е. если, тогда найдется конечное число строчных элементарных преобразований, применив которые к матрице, мы получим матрицу, строка которойимеет приведённый вид.

Действительно, если матрица имеет вид (1.1) и, то после проведения в ней элементарных преобразований

(1.20)

получаем матрицу

,

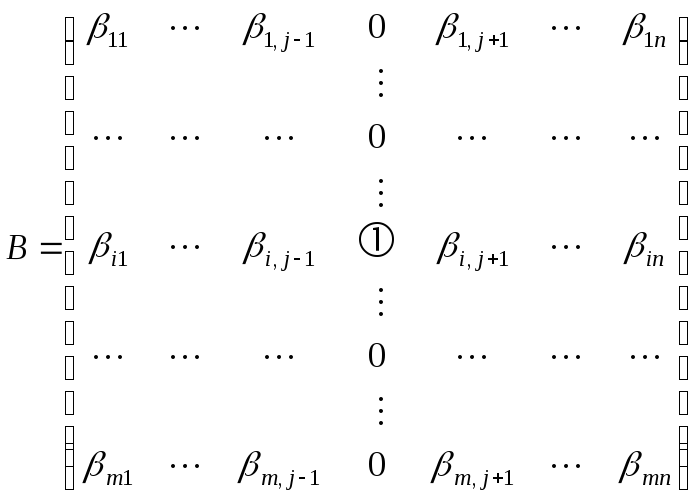у которой строка имеет приведённый вид.

Во-вторых, если строка , в матрицебыла приведённой, то после проведения элементарных преобразований (1.20) строкаматрицыбудет приведённой. Действительно, так как, приведённая, найдётся такой столбец, что

.

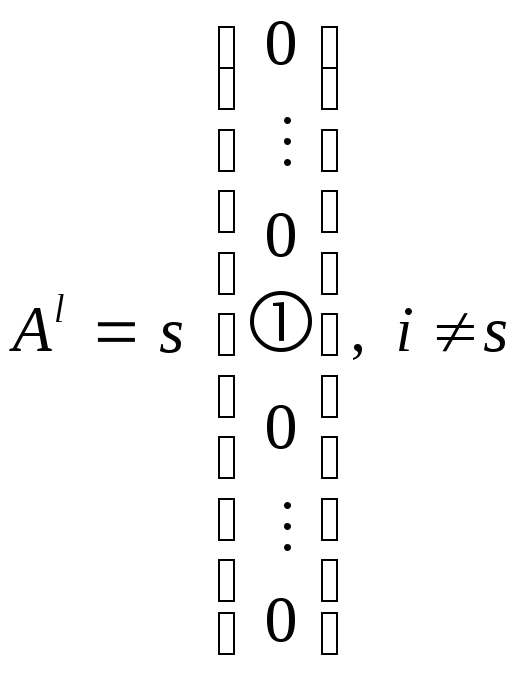но тогда и, следовательно, после проведения преобразований (1.20) столбецне меняется, т.е.. Поэтому строка, имеет приведённый вид.

Теперь ясно, что поочерёдно преобразуя указанным выше способом каждую ненулевую строку матрицы , после конечного числа шагов мы получим матрицуприведённого вида. Так как для получения матрицыиспользовались только строчные элементарные преобразования, то она л‑эквивалентна матрице. ►

Пример 7. Построить матрицу приведённого вида, л‑эквивалентную матрице

.

◄ Начиная с первой строки, указывая на каждом шаге серию проводимых элементарных преобразований, получаем

. ►

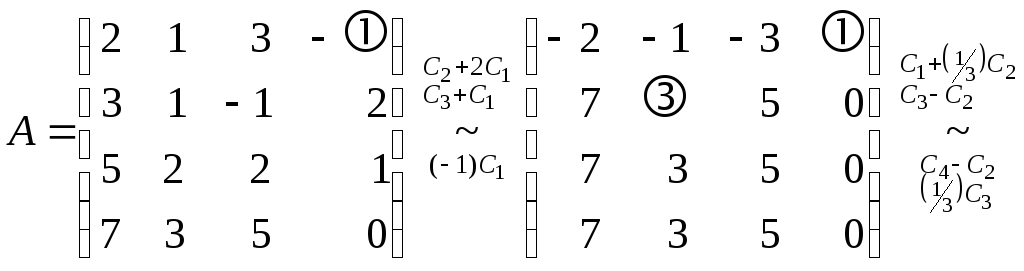
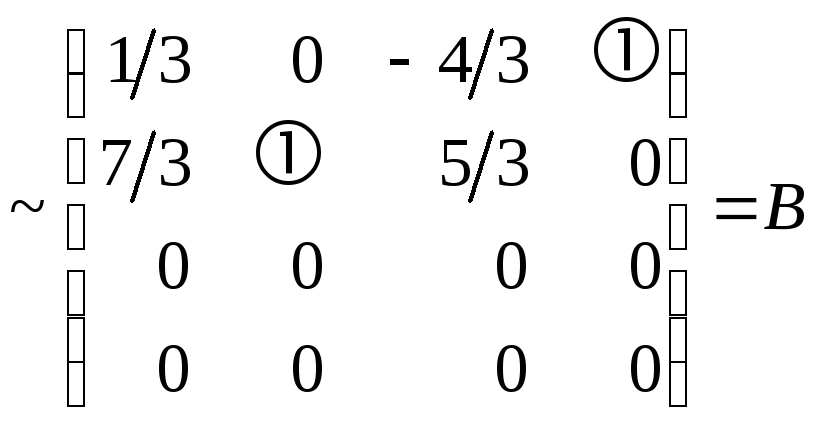Среди всех матриц размера выделим множество диагональных матриц, где, у которых

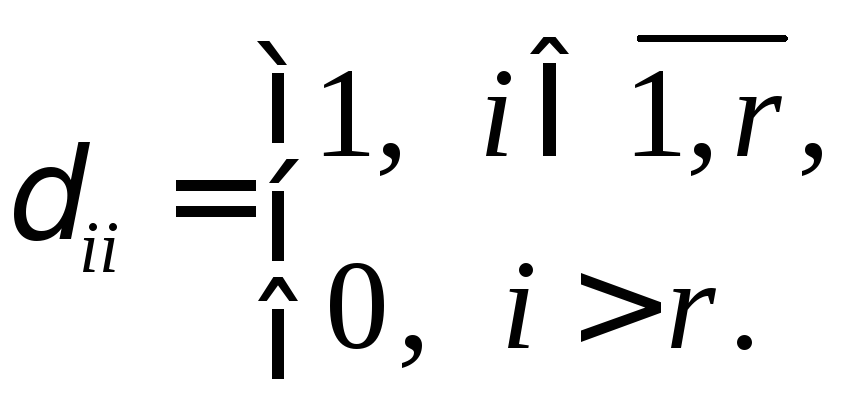
Матрицу удобно записывать в так называемом блочном виде

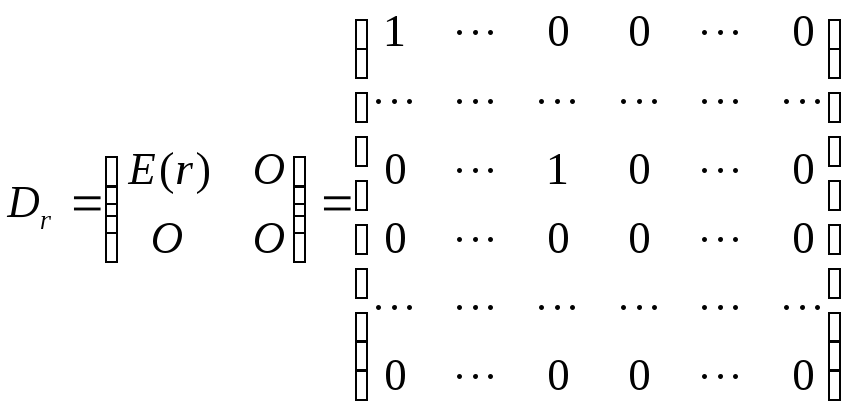, (1.21)

где единичная матрица порядка, а– обозначение, общее для нулевых блоков соответствующих размеров.

Предложение 1.4. Для любой ненулевой матрицы найдётся эквивалентная ей матрицавида(1.21).

◄ Из предложения 1.3 следует, что существует матрица приведённого вида, л‑эквивалентная, а поэтому и эквивалентная, матрице. Пусть– число ненулевых строк матрицы. Меняя местами, если это нужно, строки и столбцы матрицы, приведём её к виду

.

Проводя в матрице столбцовые элементарные преобразования

,

получим матрицу вида (1.21), эквивалентную матрице. ►