9.6. Экстраполяция и интерполяция.

Статистическая оценка возможностей развития социально-экономических явлений является важным условием регулирования рыночных отношений.

Экстраполяция – это нахождение значений функции за пределами её области определения на основе информации о поведении функции в области определения. При изучении рядов динамики это продолжение уровней ряда динамики в будущее (перспективная экстраполяция) или в прошлое (ретроспективная экстраполяция) на основе выявленной закономерности измерения уровней в изучаемом отрезке времени.

Интерполяция – это нахождение промежуточных значений функции в области её определения, т.е. в рядах динамики – для нахождения промежуточных уровней временного ряда.

Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики как базы прогнозирования, сохраняется в дальнейшем.

Важное значение при экстраполяции имеет продолжительность базисного ряда динамики и сроки прогнозирования.

Правильнее брать для экстраполяции часть ряда динамики субпериод, который является определённым этапом в развитии явления в конкретных исторических условиях. Кроме того, ем короче сроки упреждения прогноза, тем надёжнее результаты экстраполяции.

Методы экстраполяции применяются в зависимости от характера изменений в ряду динамики и задач исследования.

1) При экстраполяции на базе рядов динамики с постоянными абсолютными приростами (аналитическое выравнивание по уравнению прямой) применяется формула:

(1), где - прогнозируемый уровень,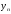- конечный уровень базисного ряда,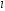- срок прогноза.

2. При экстраполяции на базе рядов динамики со стабильными темпами роста (выравнивание по уравнению показательной функции)

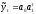(2), где - темп роста (снижения) в единицу времени.

применяется формула:

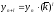(3).

В результате применения формул (1) и (3) получается точечная (дискретная) оценка. На практике экстраполяция чаще осуществляется интервальными оценками. Для определения границ интервалов используется формула:

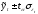(4), где - коэффициент доверия по распределению Стьюдента,- уровень значимости по таблице.

(5) - это остаточное среднее квадратическое отклонение тренда, скорректированное по числу степеней свободы (n-m). n – число уровней базисного ряда динамики, m – число параметров модели тренда.

Полученный по (2) прогноз конкретного периода корректируется на величину интервала (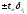), т.е. прогнозируемая на конкретный год величина явления будет иметь верхнюю и нижнюю границу.

9.7. Изучение сезонных колебаний.

Под сезонными колебаниями понимаются более/менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений (из месяца в месяц, их квартала в квартал). Ярко выраженный сезонный характер имеет сельскохозяйственное производство, туризм, спрос на ТНП в зависимости от периода времени (года). Анализ сезонных колебаний особенно необходим в маркетинговых исследованиях, когда выявляется соотношение спроса и предложения на конкретные товары и услуги и т.п.

При изучении внутригодовой динамики сезонных колебаний статистика решает две задачи:

1. выявить специфику развития явления во внутригодовой динамике;

2. измерить сезонные колебания с помощью построения модели сезонной волны.

1. Ряды внутригодовой динамики составляется по материалам текущей отчётности. Обязательно их надо привести к сопоставимому виду (сомкнуть, пересчитать в сопоставимые цены или по единой методике). Если периоды времени (месяц, квартал) разные поп продолжительности (30 дней и 31 день), то фактические величины пересчитываются в средние величины, характеризующие развитие явления в единицу времени (в день, т.е. среднедневные ).

2. Для измерения сезонных колебаний исчисляются индивидуальные индексы сезонности (1) 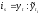, где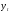- исходные уровни ряда динамики,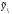- расчётные (выравненные) уровни ряда динамики (по тренду).

В (1) устраняется влияние основной тенденции на сезонные колебания. Для устранения случайных отклонений производится усреднение индивидуальных индексов i_s одноимённых периодов (месяцев, кварталов) ряда динамики.

Для каждого периода определяются средние индексы сезонности:

(2)

В зависимости от характера тренда применяются следующие формы среднего индекса сезонности:

а) если в ряду динамики основная тенденция ярко выражена (т.е. рост или снижение постоянны):

(3) 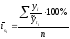-способ переменной средней.

б) если в ряду динамики отсутствует чёткий рост (снижение) уровней или он незначителен:

(4) 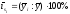- способ постоянной средней, где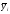- средний уровень периодаi, 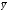- общая средняя.

Этапы исследования сезонных колебаний:

1. фактические ряды динамки приводятся к сопоставимому виду;

2. производится расчёт показателей динамики (абсолютный прирост, темпы роста, темпы прироста) и определяется тенденция ряда к росту (снижению) или её отсутствие и, следовательно, способ расчёта индекса сезонности: способ переменной средней или способ постоянной средней;

3. подбирается математическая функция, по которой будет производиться аналитическое выравнивание и определяться теоретические (расчётные) уровни (). Обычно выбирается несколько математических функций (прямая, парабола, гипербола и т.п.); оптимальная определяется по минимальному уровню ошибки аппроксимации;

4. рассчитываются теоретические уровни ряда динамики; потом индивидуальные индексы сезонности для каждого периода;

5. рассчитываются средние индексы сезонности по способу, выбранному в п.2.

6. строится график (сезонная волна) роста (снижения) объёмного показателя.

Для выявления сезонных колебаний можно применять метод скользящей средней.

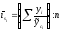, где - число одноимённых периодов,- уровни рядов динамики, сглаженные по средней.