
- •Общая теория статистики
- •Часть 2
- •Тема 8. Выборочное наблюдение.
- •8.1. Понятие выборочного наблюдения.
- •8.2. Понятие ошибки выборки.
- •8.3. Определение необходимой численности выборки.
- •8.4. Способы распространения выборочных характеристик на генеральную совокупность.
- •8.5. Способы образования выборочной совокупности.
- •Тема 9. Статистические ряды динамики.
- •9.1. Понятие статистических рядов динамики.
- •9.2. Сопоставимость в рядах динамики.
- •9.3. Система показателей динамики.
- •9.4. Средние показатели рядов динамики.
- •9.5. Приемы анализа рядов динамики.
- •9.6. Экстраполяция и интерполяция.
- •9.7. Изучение сезонных колебаний.
- •Тема 10. Индексный метод.
- •10.1. Понятие и классификация индексов.
- •10.2. Агрегатные индексы. Система индексов.
- •10.3. Средние индексы.
- •10.4. Цепные и базисные индексы.
- •10.5. Изучение индексным методом влияния структурных сдвигов.
- •10.6. Территориальные индексы.
- •Тема 11. Статистическое изучение взаимосвязей явлений.
- •11.1. Задачи статистики в изучении взаимосвязи явлений.
- •11.2. Методы корреляционно-регрессионного анализа связи.
- •11.3. Корреляционно-регрессионный анализ связи парной корреляции.
- •11.4. Понятие множественной регрессии.
11.3. Корреляционно-регрессионный анализ связи парной корреляции.
Парная корреляция (рассматривалась во втором вопросе) – методология, рассматривающая влияние вариации факторного признака x на результат y, т.е. взаимосвязь пары признаков x и y. Применение: на примере – выбрать адекватную модель (на базе данных по однотипным предприятиям зависимости затрат на ремонт оборудования от возраста оборудования.
|
№
|
Возраст оборудования; лет
|
Затраты на ремонт, тыс. руб.
|
по прямолинейной |
по логарифми-ческой |
по показа-тельной |
|
1 |
4 |
1,5 |
0,868 |
0,65 |
1,36 |
|
2 |
5 |
2,0 |
1,479 |
1,54 |
1,64 |
|
3 |
5 |
1,4 |
1,479 |
1,54 |
1,64 |
|
4 |
6 |
2,3 |
2,090 |
2,27 |
1,99 |
|
5 |
8 |
2,7 |
3,312 |
3,42 |
2,93 |
|
6 |
10 |
4,0 |
4,534 |
4,31 |
4,31 |
|
7 |
8 |
2,3 |
3,312 |
3,42 |
2,93 |
|
8 |
7 |
2,5 |
2,700 |
2,89 |
2,41 |
|
9 |
11 |
6,6 |
5,145 |
4,70 |
5,23 |
|
10 |
6 |
1,7 |
2,090 |
2,27 |
1,99 |
|
Итого: |
70 |
27,0 |
27,009 |
27,01 |
26,43 |
Определяется путём перебора наиболее часто применяемых уровней регрессии:
а)
прямолинейной функции: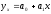 ;
;
б)
логарифмической функции:
 ;
;
в)
показательной функции:
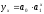 .
.
Сравниваться должны два критерия: остаточная дисперсия – должна быть минимальна для определения адекватных моделей и средняя ошибка аппроксимации – должна быть минимальна.
Параметры находятся по методу наименьших квадратов, для показательной – через логарифм.
а)
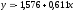 , б)
, б)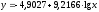 , в)
, в)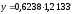 .
.
Параметры
проверяются на типичность, для чего
рассчитывается
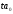 и
и
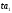 -фактические,
число степеней свободы
-фактические,
число степеней свободы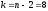 и через
и через
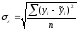 и
и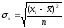 .
.
а)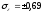 б)
б)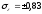 в)
в)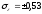
остаточная
дисперсия а)
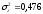 б)
б)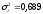 в)
в)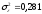 .
.
Параметры везде получаются значимы.
Практическая
значимость моделей оценивается по R(r):
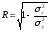 и
и
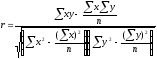
а)
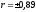 б)
б)
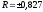 в)
в)
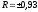
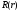 проверяется
по F-крит.
с
проверяется
по F-крит.
с
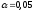 ,
,
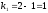
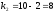 –везде
значимы.
–везде
значимы.
а)
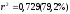 – может быть использована для практических
целей;
– может быть использована для практических
целей;
б)
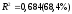 – может быть пригодна;
– может быть пригодна;
в)
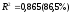 – может быть пригодна.
– может быть пригодна.
Далее модели проверяются на адекватность через показатель средней ошибки аппроксимации.
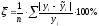
а)
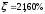 б)
б)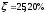 в)
в)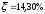 .
.
Следовательно, наиболее адекватной является экономико-математическая модель, построенная по показательной функции.
11.4. Понятие множественной регрессии.
На практике чаще всего возникает необходимость исследовать зависимость результативного признака от нескольких факторных признаков. Тогда статистическая модель представляется уравнением регрессии с несколькими переменными величинами. Такая регрессия называется множественной.
Множественная линейная регрессия имеет вид:
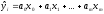 , где
, где
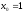 – фиктивная переменная.
– фиктивная переменная.
Параметры уравнения определяются МНК, при этом значения x и y представляются в матричном виде:
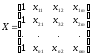 матрица
матрица
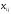 - значений независимых переменных.
- значений независимых переменных.
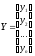 вектор
значений зависимый переменной
вектор
значений зависимый переменной
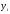 .
.
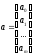
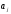 - вектор оценок параметров.
- вектор оценок параметров.
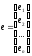 вектор
ошибок
вектор
ошибок
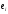 .
.
Тогда: линейная модель в векторном виде
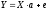 .
.
Вектор
оценки
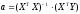 ,
где
,
где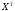 - транспонированная
матрица, строки исходной матрицы в
транспонированной становятся столбцами,
- транспонированная
матрица, строки исходной матрицы в
транспонированной становятся столбцами,
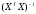 - обратная матрица.
- обратная матрица.
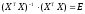 ,
где
,
где
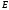 - единичная матрица.
- единичная матрица.
 .
.
Например, сравнить параметры (коэффициенты регрессии) в уравнении нельзя, если они не выражаются в одинаковых единицах.
Для
сравнения применяют нормированные
коэффициенты регрессии
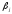 (бетта-коэффициент):
он показывает величину изменения
результативного признака при изменении
факторного признака
(бетта-коэффициент):
он показывает величину изменения
результативного признака при изменении
факторного признака
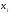 на
одну среднюю квадратическую ошибку (в
единицах измерения ошибки):
на
одну среднюю квадратическую ошибку (в
единицах измерения ошибки):
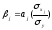 , где
, где
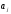 - параметр
при
- параметр
при
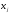 факторе,
факторе,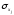 -
средне квадратическое отклонение
факторного признака,
-
средне квадратическое отклонение
факторного признака, - среднее квадратическое отклонение
результативного признака.
- среднее квадратическое отклонение
результативного признака.
Анализ дополняется расчётом коэффициента эластичности факторных признаков
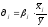 - он
показывает, на сколько процентов
изменится результативный признак
- он
показывает, на сколько процентов
изменится результативный признак
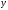 ,
если
факторный признак
,
если
факторный признак
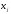 изменится на 1%, а остальные факторы
будут зафиксированы на каком-либо уровне
(среднем).
изменится на 1%, а остальные факторы
будут зафиксированы на каком-либо уровне
(среднем).
Те
факторы, у которых
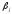 и
и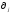 большие, по сравнению с другими, сильно
влияют на результативный признак, а те,
у которых
большие, по сравнению с другими, сильно
влияют на результативный признак, а те,
у которых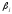 и
и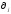 незначительны,
- слабо влияют и могут быть отброшены.
незначительны,
- слабо влияют и могут быть отброшены.
Рассчитывается
также коэффициент множественной
корреляции – он показывает тесноту
связи результативного признака
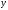 со
всеми факторными признаками
со
всеми факторными признаками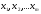 .
.
Для линейной функции он:
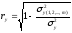 ,
, 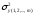 - остаточная дисперсия,
- остаточная дисперсия,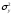 - дисперсия результативного признака.
- дисперсия результативного признака.
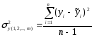 ,
,
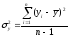 .
.
Коэффициент
множественной детерминации =
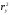 .
.
Рост множественного коэффициента корреляции обеспечивается включением в модель факторных признаков. Для оценки вклада каждого фактора применяют частные коэффициенты корреляции. Частный коэффициент корреляции – показатель, характеризующий тесноту связи между признаками при элиминации всех остальных признаков.
Список литературы.
Положение “О государственном комитете Российской Федерации по статистике”. Утверждено постановлением Правительства Российской Федерации от 9 июля 1994 г., №834.
Постановление Главы Администрации (губернатора) Омской области от 15 февраля 2000 г. № 50-п “О Всероссийской переписи населения 2002 г. на территории Омской области”.
Общая теория статистики: Учебник. / Под ред. А.А.Спирина, О.Э.Башиной. – М.: Финансы и статистика, 1994.
Омская область в цифрах “1998”: Статистический сборник – Омск: Омский областной комитет государственной статистики, 1999.
Омская область в цифрах “1999”: Статистический сборник – Омск: Омский областной комитет государственной статистики, 2000.
Практикум по теории статистики: Учебное пособие. / Под ред. проф. Р.А.Шмойловой. – М.: Финансы и статистика, 1999.
Социально-экономическое положение г. Омска за январь-июнь 1998 г.: Статистический бюллетень. – Омск: Омский областной комитет государственной статистики, 1998.
Статистика: Курс лекций. / Под ред. к.э.н. В.Г.Ионина – Новосибирск: Издательство НГАЭиУ, М.: ИНФРА-М, 1998.
Статистическйи словарь. / Гл.ред. Ю.А. Юрков – М.: Финстат-информ, 1996.
