
Лекция дискрет 04 (1)
.pdf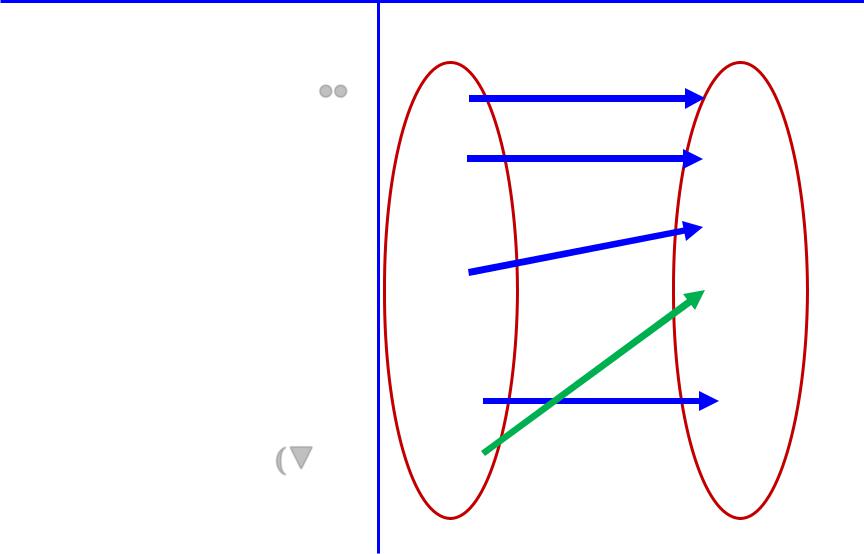
{ m1, m2, … , mk, mk+1 } = M ≈ Nk+1 = { 1, 2, … , k, k+1 }
Допустим противное:
В М, B , В ≈ М ( )
Тогда существует
взаимно однозначное
соответствие f: M B
Пусть при этом
соответствии
f (mk+1) = mq (▼)
M |
f: M B |
|
|
m1 |
|
m2 |
|
…..
mq
…..
mk
mk+1
..... |
B |
|
|
….. |
|
….. |
|
mq |
|
….. |
|
….. |
|
….. |
|

Определим вспомогательное взаимно однозначное соответствие g: M M следующим образом:
g (mq) = mk+1 g (mk+1) = mq (▼▼)
g (mi) = mi для всех i=1,2,…,k,k+1 (i q, i k+1)
(по построению очевидно, что g: Μ Μ – взаимно однозначное соответствие)
Рассмотрим суперпозицию h: M B, т.е. h (mi) = f (g (mi))
В силу (▼▼) и (▼): h (mq) = f (g (mq)) = f (mk+1) = mq h (mk+1) = f (g (mk+1)) = f (mq)
h (mi) = f (g (mi)) = f (mi) для прочих i
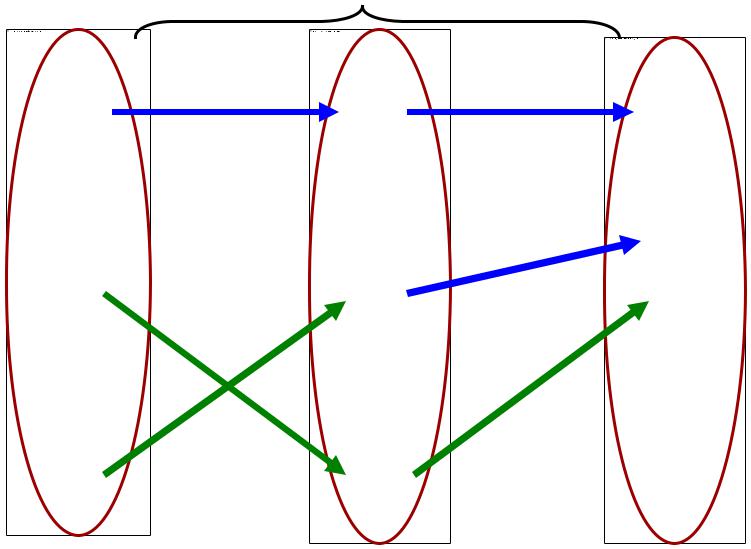
h: M B
M |
g: M M |
M f: M B |
|
m1 |
m1 |
||
|
m2  m2
m2 
….. …..
mq |
mq |
….. …..
mk  mk
mk 
mk+1 |
mk+1 |
..... |
B |
|
…..
…..
mq
…..
…..
…..

Определённое таким образом соответствие h: M B – взаимно однозначное, так как:
Соответствие h – всюду определено, так как g всюду определено, и h – сюръективно, так как f сюръективно.
Функциональность. Возьмём произвольный mi М. При соответствии g Char(mi) ≠ в силу функциональности g. Также в силу функциональности g Char(mi) не может включать два различных элемента из М. Итак, g (mi) = mi .
Аналогично, при соответствии f невозможно Char(mi ) = в силу функциональности f, по той же причине Char(mi ) не
может состоять из двух различных элементов из В, поэтому f (mi ) = mi .
Но mi = f (mi ) = f (g (mi)) = h (mi), т.е. h – функционально.

Инъективность. Возьмём произвольный mi B. При соответствии f Prot(mi ) ≠ в силу инъективности f. Также в силу инъективности f Prot(mi ) не может включать два различных элемента из М. Итак, mi = f (mi ).
Аналогично, при соответствии g невозможно Prot(mi ) = в силу инъективности g, по той же причине Prot(mi ) не
может состоять из двух различных элементов из М, т.е. : mi = g (mi).
Но mi = f (mi ) = f (g (mi)) = h (mi), т.е. h – инъективно.
Итак, доказали, что h: M B – взаимно однозначное
Построим соответствие h : M B , где:
M = M \ { mq } B = B \ { mq } |
h (mi) = f (g (mi)) |
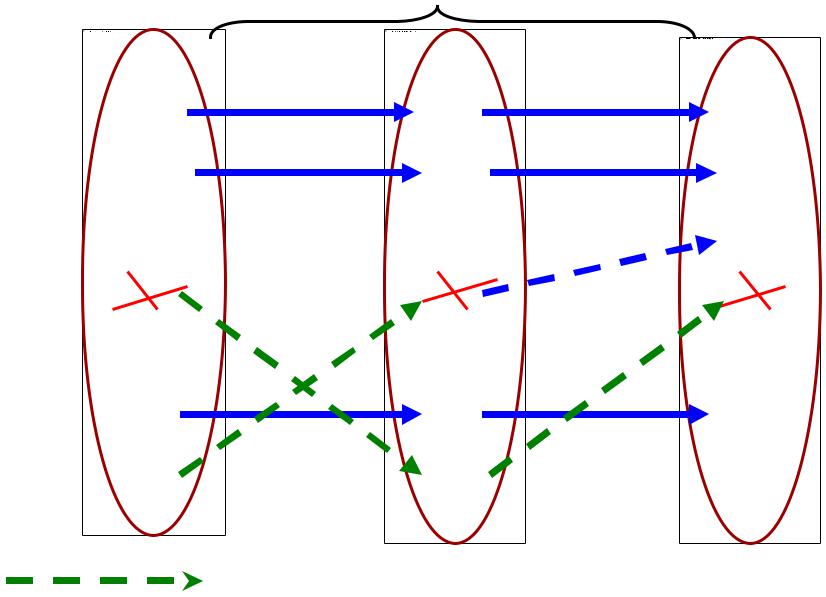
|
h : M B |
|
|||
M |
g : M M |
M |
f : M B |
B |
|
m1 |
m1 |
..... |
|||
|
|
||||
|
m2 |
m2 |
….. |
|
|
|
….. |
….. |
….. |
|
|
|
mq |
mq |
mq |
|
|
|
….. |
….. |
….. |
|
|
|
mk |
mk |
….. |
|
|
|
mk+1 |
mk+1 |
….. |
|
|
|
Не стало |
|
|
|
|

Построили соответствие h : M B , где:
M = M \ { mq } B = B \ { mq }
h (mi) = f (g (mi))
Множество M = M \ { mq } содержит ровно k элементов и, в силу индукционного предположения ( ), в М не имеется собственных подмножеств, равномощных М
Доопределим соответствия f и g так, как это показано на схеме.
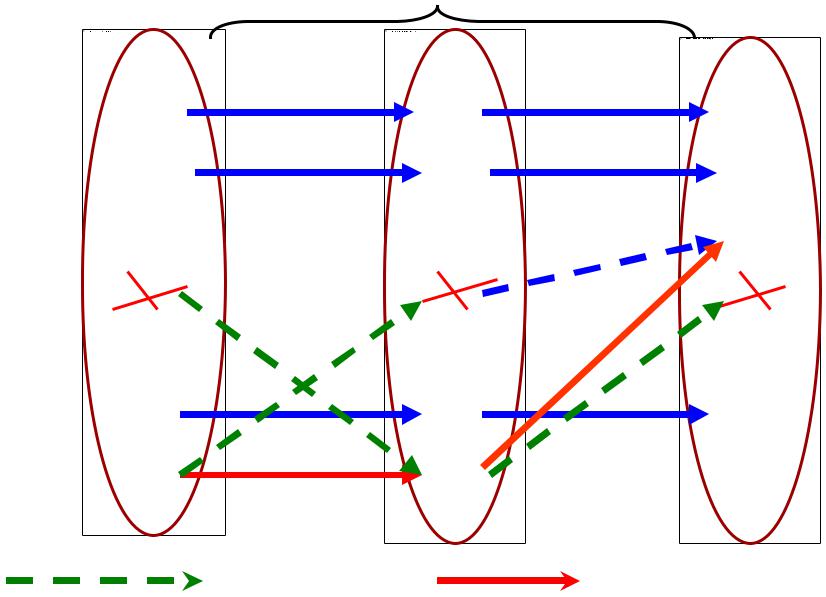
|
h : M B |
|
|||
M |
g : M M |
M |
f : M B |
B |
|
m1 |
m1 |
..... |
|||
|
|
||||
|
m2 |
m2 |
….. |
|
|
|
….. |
….. |
….. |
|
|
|
mq |
mq |
mq |
|
|
|
….. |
….. |
….. |
|
|
|
mk |
mk |
….. |
|
|
|
mk+1 |
mk+1 |
….. |
|
|
|
Не стало |
|
Новое |
|
|
|
|
|
|
||

Легко доказать, что h : M B - взаимно однозначное соответствие, значит, собственное подмножество В М равномощно М
Пришли к противоречию, значит, допущение ( )
отом, что В М, B , В ≈ М – неверно.
Всилу принципа математической индукции: при любом значении k конечное множество
М= { m1, m2, … , mk } ≈ Nk = { 1, 2, … , k }
не может быть равномощно никакому своему собственному подмножеству М1 (M1 M M1 ≠ M)
Доказано Th.1.4.2

Th.1.4.3 Конечное множество М1 не может быть равномощно никакому множеству М2 такому, что М1 М2
Доказательство Th.1.4.3
Если множество М2 – бесконечное, то согласно замечанию в начале доказательства Th.1.4.2 оно заведомо не может быть равномощно конечному множеству М1. Поэтому достаточно рассмотреть случай конечного множества М2.
Но согласно Th.1.4.2 конечное множество М2 не может иметь в качестве собственного подмножества никакое равномощное ему конечное множество М1.
Доказано Th.1.4.3
