
Лекция дискрет 08
.pdfПорядок анализа алгебры типа (2, 2) на примере [ R; +, ]
дистрибутивность ( ) слева и справа относительно (+)
[ R; + ] – абелева группа:
a ( b + c ) = a b + a c ( a + b ) c = a c + b c
(+)- ассоциативная
(+)- коммутативная нейтральный элемент обратный элемент
a + (b + c) = (a + b) + c a + b = b + a
a + 0 = 0 + a = a a + (- a) = 0
[ R; +, ] - кольцо
обратный эл-т относительно ( ) |
a a -1 = 1 |
[ R; +, ] - тело |
|
( ) - коммутативная |
a b = b a |
[ R; +, ] - поле |
|

§2.2. Примеры алгебр
1)Примеры применения теории полугрупп / групп
Исходные понятия теории полугрупп и простейшие свойства полугрупп достаточно элементарны и вполне доступны школьникам старших классов. Более того, можно сказать, что с полугруппами встречается, не подозревая этого, уже первоклассник, и затем они сопровождают учащихся на протяжении всех лет обучения в школе.
Лев Шеврин (Екатеринбург)
... я склонен верить, что в действительности понятие группы является древнейшим математическим понятием, более древним, чем понятие числа, и неотделимым от самой человеческой цивилизации.
Н.А.Вавилов (Санкт-Петербург)
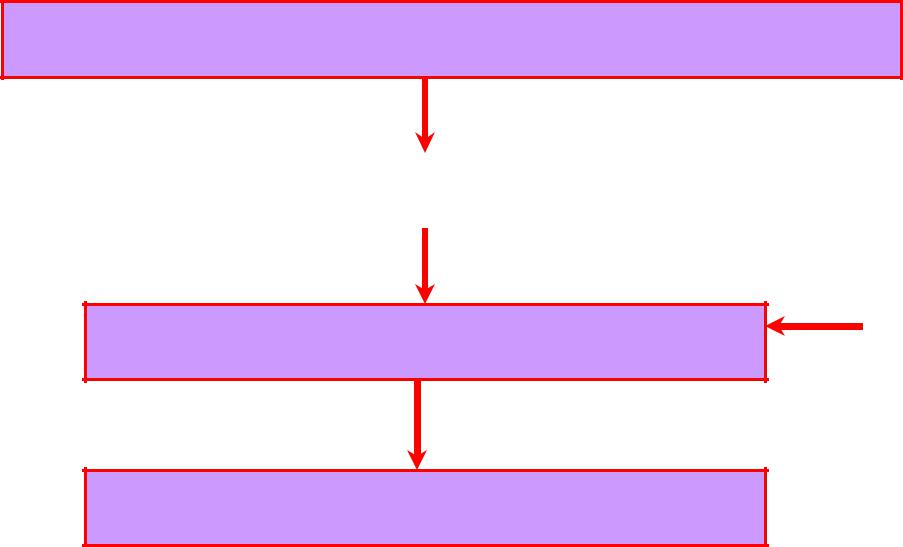
Алгебра типа (2) - [аддитивная / мультипликативная] полугруппа / группа
Полугруппа – алгебра с одной ассоциативной операцией
|
+ коммутативность |
элемент |
|
|
|
|
Абелева (коммутативная) полугруппа |
|
|
|
нейтральный+ |
+ обратный элемент |
||
+ нейтральный элемент Моноид
Группа
Примеры групп и полугрупп из § 2.1:
[ R \ { 0 }; ] – мультипликативная коммутативная группа
[ N- { 0 } N+; + ] – аддитивная коммутативная группа
[ {Mn}; ] – мультипликативная некоммутативная группа
({Mn} – множество любых квадратных матриц n-ого порядка;- матричное умножение)
[ {Mn}; ] – мультипликативный некоммутативный моноид
(единица – матрица с единичной диагональю; {Mn} – множество невырожденных квадратных матриц n-ого порядка;- матричное умножение)
[ B (M); ] – аддитивный коммутативный моноид (ноль –
пустое множество )
[ B (M); ] – мультипликативный коммутативный
моноид (единица – множество М, выполняющее роль универсума)
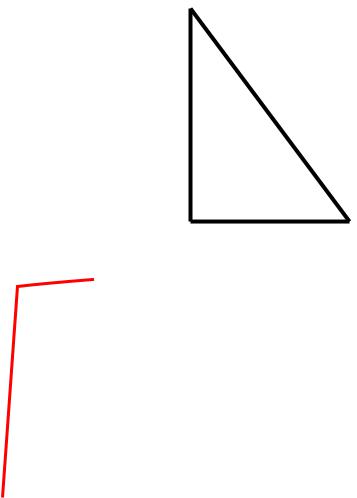
а) Пифагоровы тройки |
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Натуральные числа a, b, c |
|
|
|
c |
|||
– пифагорова тройка, |
|
|
a |
|
|||
если a2 + b2 = c2 |
|
|
|
|
|||
|
|
|
|
||||
Например: (3, 4, 5), (6, 8, 10), (5, 12, 13), |
|
|
b |
||||
(9, 12, 15), (8, 15, 17), (12, 16, 20), |
|
|
|
||||
|
|
|
|
||||
Обобщённая |
|
||||||
(15, 20, 25), (7, 24, 25), (10, 24, 26), |
|
||||||
пифагорова тройка: |
|||||||
(20, 21, 29), (18, 24, 30), (16, 30, 34), |
|||||||
допустима возможность |
|||||||
(21, 28, 35), (12, 35, 37), (15, 36, 39), |
|||||||
целых отрицательных, |
|||||||
(24, 32, 40), (9, 40, 41), (27, 36, 45), |
|||||||
а также нулевых |
|||||||
(14, 48, 50), (30, 40, 50), … |
|||||||
значений a, b, c |
|||||||
|
|
|
|||||
y |
|
|
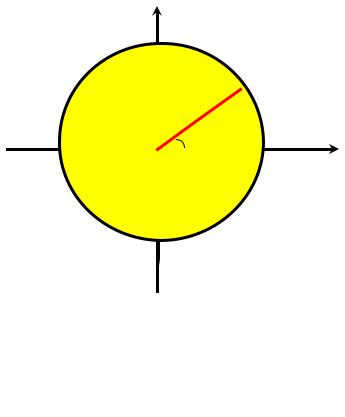
Строим формальную модель: |
|
|
|
|
||
c |
|
b |
|
Каждой обобщённой пифагоровой |
|
|
|||
|
|
тройке соответствует рациональная |
||
α |
|
x |
||
|
|
|
||
a |
|
|
|
точка на единичной окружности: |
|
|
|
||
координаты (x, y) - рациональные числа, т.е. имеют вид (a/c, b/c)
Например, точки (3/5, 4/5), (0,1), (−5/13,12/13) являются рациональными точками, а (1/2, 3 /2) — не является рациональной точкой.
Рациональная точка с координатами (a/c, b/c) однозначно определена углом α, при этом:
Sin α = |
b |
Cos α = a |
|
|
|||
c |
|||
|
c |
Обозначим: Z = N- {0} N+
P = { (a, b, c): a Z, b Z, c Z, a2 + b2 = c2 }
Введём функцию следующим образом:
(a3, b3, c3) = (a1, b1, c1) (a2, b2, c2)
Пусть:
тройка (a1, b1, c1) определена углом α1 тройка (a2, b2, c2) определена углом α2
Тогда результатом выполнения функции примем по
определению тройку (a3, b3, c3), которая соответствует |
|
углу α3 = α1 + α2 |
Получили структуру [ P; ] |
Докажем, что множество P замкнуто относительно - если (a1, b1, c1) и (a2, b2, c2) – обобщённые пифагоровы тройки, то и
тройка (a3, b3, c3) = (a1, b1, c1) (a2, b2, c2) также обобщённая пифагорова. Это будет означать, что - бинарная операция на
множестве P
Доказываем замкнутость множества P относительно
(a3, b3, c3) = (a1, b1, c1) (a2, b2, c2) = α1 + α2 = α3
Иными словами: докажем, что если α1 и α2 определяют обобщённые пифагоровы тройки, то α3 также определяет обобщённую пифагорову тройку
α3 = α1 + α2 = arcsin (b1 / c1) + arcsin (b2 / c2) =
=arcsin ((b1 / c1) (1 - (b2 / c2)2)½ + (b2 / c2) (1 - (b1 / c1)2)½ ) =
=arcsin ((b1 / c1) ((c22 - b22) / c22)½ + (b2 / c2) ((c12 – b12) / c12)½ ) =
=arcsin ((b1 / c1) (a22 / c22)½ + (b2 / c2) (a12 / c12)½ ) =
=arcsin ((b1 / c1) (a2 / c2) + (b2 / c2) (a1 / c1) ) =
=arcsin ((a1b2 + a2b1) / (c1c2))
Получили: Sin α3 = (a1b2 + a2b1) / (c1c2) = b3 / c3
a1b2 + a2b1 и c1c2 – целые числа, поэтому α3 определяет рациональную точку
Аналогично: Cos α3 = (a1a2 - b1b2) / (c1c2) = a3 / c3
Итак: |
a3 = a1a2 – b1b2 |
|
b3 = a1b2 + a2b1 |
|
c3 = c1c2 |
Проверяем, что a32 + b32 = c32, т.е. вычисленная тройка (a3, b3, c3) – обобщённая пифагорова
Для этого достаточно убедиться, что
(a1a2 – b1b2)2 + (a1b2 + a2b1)2 = (c1c2)2

(a1a2 – b1b2)2 + (a1b2 + a2b1)2 = (c1c2)2
a |
2a 2 |
– 2a |
1 |
a |
b |
b |
2 |
+ b |
2b 2 |
+ a |
2b 2 |
+ 2a |
1 |
a |
b |
b |
2 |
+ a |
2b 2 |
= c |
2c 2 |
|||||||
1 |
2 |
|
2 |
1 |
|
|
1 |
|
2 |
1 |
|
2 |
|
|
2 |
|
1 |
|
|
|
2 |
1 |
1 |
2 |
||||
|
|
|
|
a |
2a 2 |
+ b |
|
2b 2 |
+ a |
|
2b 2 + a |
2b 2 |
= c |
2c |
2 |
|
|
|
||||||||||
|
|
|
|
1 |
2 |
|
|
1 |
2 |
1 |
2 |
2 |
|
|
1 |
|
|
|
1 |
2 |
|
|
|
|||||
|
|
|
|
|
a 2(a 2 |
+ b 2) + b |
2(a |
2 + b |
|
2) = c |
2c |
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
2 |
1 |
2 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|||||
(a12 + b12) × (a22 + b22) = c12× c22
c12× c22 = c12× c22
