
Лекция дискрет 08
.pdf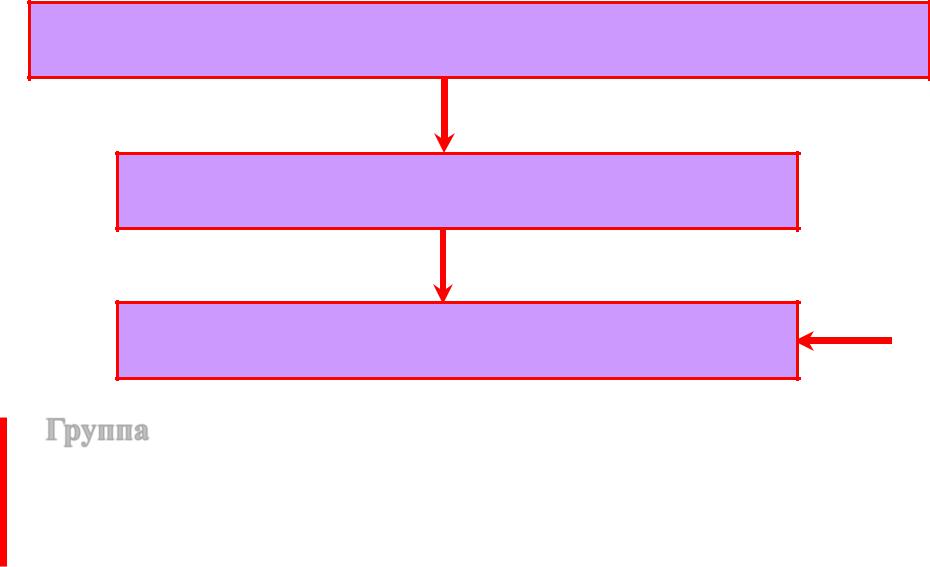
[аддитивная/мультипликативная] алгебра типа (2)
Полугруппа – алгебра с одной ассоциативной операцией
+ коммутативность
Абелева (коммутативная) полугруппа
+ нейтральный элемент
Моноид
Группа – моноид, в котором для каждого элемента существует обратный. В зависимости от других признаков группа может быть аддитивной / мультипликативной, коммутативной (абелевой) / некоммутативной
[аддитивная/мультипликативная] алгебра типа (2)
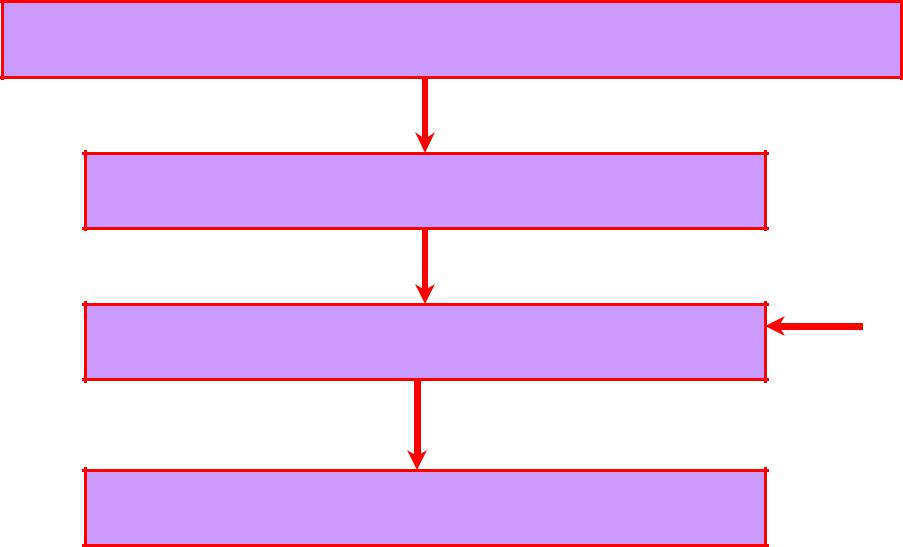
Полугруппа – алгебра с одной ассоциативной операцией
+ коммутативность
Абелева (коммутативная) полугруппа
+ нейтральный элемент
Моноид
+ обратный элемент
Группа
+ нейтральный элемент
Примеры:
[ R \ { 0 }; ] – мультипликативная коммутативная группа
[ N- { 0 } N+; + ] – аддитивная коммутативная группа
[ {Mn}; ] – мультипликативный некоммутативный
моноид ({Mn} – множество любых квадратных матриц n-ого порядка; единица – матрица с единичной главной диагональю и нулями в остальных позициях) Обратный элемент не определён для вырожденных матриц, то есть данный моноид группой не является
Но если {Mn} – множество невырожденных
квадратных матриц n-ого порядка, то получаем мультипликативную некоммутативную группу
Примеры: |
[ B (M); ] |
[ B (M); ] |
|
|
A B (M), B B (M), С B (M) |
||
Замкнутость B (M) |
|
|
|
A B B (M) |
A B B (M) |
||
относительно ( ) |
|||
|
|
||
|
|
|
|
Ассоциативность |
(A B) C = |
(A B) C = |
|
операций ( ) |
A (B C) |
A (B C) |
|
|
|||
|
|
|
|
Коммутативность |
A B = B A |
A B = B A |
|
операций ( ) |
|||
|
|
||
|
|
|
|
Нейтральный элемент |
, так как А = А |
М, так как А М = А |
|
относительно ( ) |
|||
|
|
||
|
|
|
|
Обратный элемент |
Отсутствует решение |
Отсутствует решение |
|
относительно ( ) |
А X = |
А X = M |
|
|
|
|
|
|
Коммутативный |
Коммутативный |
|
|
аддитивный |
мультипликативный |
|
|
моноид [ B (M); ] |
моноид [ B (M); ] |
|
|
|
|
|

Алгебры типа (2,2) с одной аддитивной и одной мультипликативной операцией
Алгебра типа (2,2) [ M; +, ] с одной аддитивной и одной мультипликативной операцией называется кольцом, если:
-мультипликативная операция ( ) дистрибутивна слева и справа относительно аддитивной операции (+);
-алгебра [ M; + ] – абелева группа.
Пример 1:
алгебра [ R; +, ] – кольцо действительных чисел:
-дистрибутивность ( ) относительно (+) – имеется;
-[ R; + ] – абелева группа, так как (а) – операция (+) ассоциативна и коммутативна; (b) имеется нейтральный
элемент – нулевой; (с) обратным элементом для любого r R является число (-r)

алгебра типа (2,2)
|
Алгебра [ M; +, ] с одной аддитивной |
||
|
и одной мультипликативной операцией |
||
+ дистрибутивность слева и |
+ алгебра [ M; + ] – абелева |
||
справа операции ( ) |
|||
группа |
|||
|
|
||
относительно операции (+) |
|
||
Пример 2: |
Кольцо |
|
|
|
|
Алгебра [ {Mn}; +, ] – кольцо квадратных матриц n-ого порядка:
-дистрибутивность ( ) относительно (+) – имеется;
-[ {Mn}; + ] – абелева группа, так как (а) – операция (+)
ассоциативна и коммутативна; (b) имеется нейтральный элемент – нулевая матрица; (с) обратным элементом для любой матрицы является матрица с противоположными значениями элементов
{Mn} – множество произвольных квадратных матриц n-ого
порядка; операции – согласно теории матриц
алгебра типа (2,2)
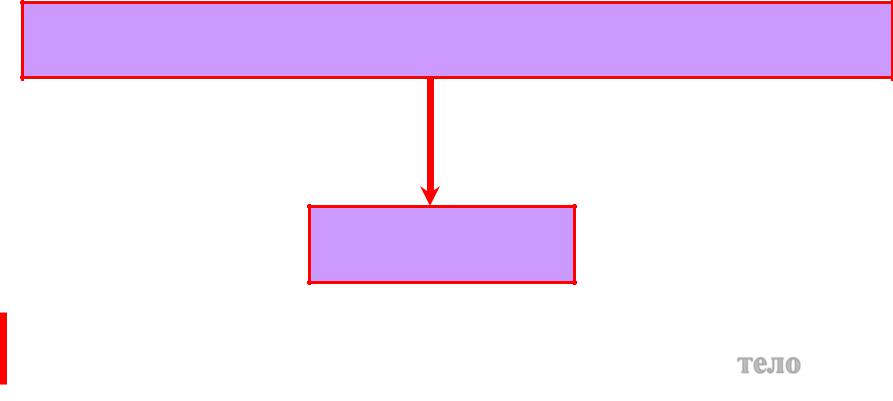
Алгебра [ M; +, ] с одной аддитивной и одной мультипликативной операцией
+ дистрибутивность слева и |
+ алгебра [ M; + ] – абелева |
|
справа операции ( ) |
||
группа |
||
|
||
относительно операции (+) |
|
Кольцо
Кольцо, в котором все ненулевые элементы имеют обратные относительно мультипликативной операции ( ) - тело
Пример 1:
Кольцо действительных чисел [ R; +, ] для каждого числа r 0 содержит число 1/r
Получили тело действительных чисел [ R; +, ]
алгебра типа (2,2)
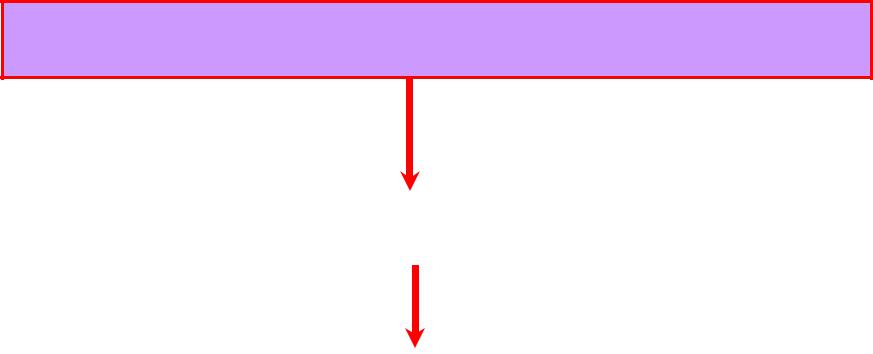
Алгебра [ M; +, ] с одной аддитивной и одной мультипликативной операцией
+ дистрибутивность слева и |
+ алгебра [ M; + ] – абелева |
|||||
справа операции ( ) |
||||||
группа |
|
|
||||
|
|
|
|
Пример 2: |
||
относительно операции (+) |
|
|
||||
|
|
|
Кольцо |
|
Кольцо произвольных |
|
|
|
|
|
|
квадратных матриц n-ого |
|
+ обратный элемент |
|
|||||
|
|
порядка [ {Mn}; +, ] – не |
||||
относительно операции ( ) |
|
|
обеспечено |
|||
|
|
|
|
|
существование обратного |
|
|
|
|
Тело |
|
||
|
|
|
|
элемента (в {Mn} |
||
|
|
|
|
|
содержатся вырожденные |
|
|
|
|
|
|
||
|
|
|
|
|
матрицы) |
|
Сужение {Mn} до множества невырожденных матриц ничего не даёт: не будет нуль-матрицы, а, значит, и абелевой группы [ {Mn}; + ] – то есть и кольца не получится

Алгебра типа (2,2) [ M; +, ] с одной аддитивной и одной мультипликативной операцией называется кольцом, если:
-мультипликативная операция ( ) дистрибутивна слева и справа относительно аддитивной операции (+);
-алгебра [ M; + ] – абелева группа.
Кольцо, в котором все ненулевые элементы имеют обратные относительно мультипликативной операции ( ) - тело
Если в теле мультипликативная операция ( ) коммутативна, то тело [ M; +, ] называется полем
Пример:
В теле действительных чисел [ R; +, ] операция умножения коммутативна
Получили поле действительных чисел [ R; +, ]

Обобщение для фундаментальных алгебр типа (2,2)
Алгебра [ M; +, ] с одной аддитивной и одной мультипликативной операцией
+ дистрибутивность слева и |
+ алгебра [ M; + ] – абелева |
|
справа операции ( ) |
||
группа |
||
|
||
относительно операции (+) |
|
Кольцо
+ обратный элемент относительно операции ( )
Тело
+ коммутативность операции ( )
Поле
