Лекция дискрет 12

4) Функционально полные системы логических функций

1. Символы переменных x1, x2, … , xn, … - логические формулы глубины 0 над множеством логических функций Σ.

2. Пусть F1, F2, … , Fni – логические формулы глубины не более k над множеством логических функций Σ, причём хотя бы одна из них имеет глубину ровно k. Пусть также

fi ( x1, x2, … , xni ) Σ – логическая функция.

Тогда fi ( F1, F2, … , Fni ) – логическая формула глубины (k+1) над множеством логических функций Σ.

3. Других логических формул над множеством логических функций Σ нет.

Система логических функций Σ называется полной (функционально полной), если любая логическая функция может быть представлена логической формулой над Σ

Σ0 = { , &, - функционально полная (Th.3.2.1) Th.3.2.4

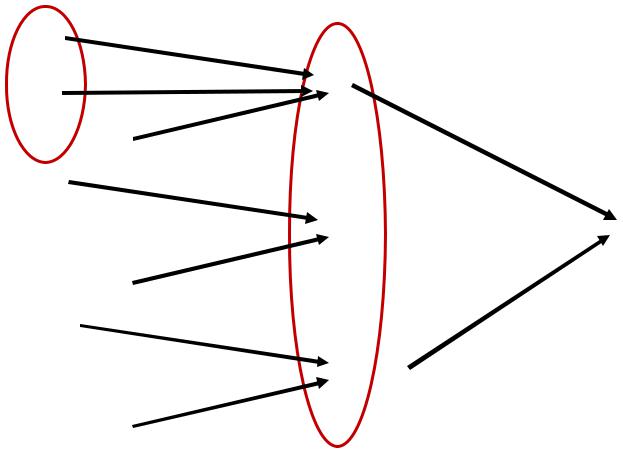
Заданы две системы логических функций:

Система Σ* - функционально полная и любая логическая функция из Σ* может быть реализована формулой над Σ.

Тогда система Σ – функционально полная

……………

g1

g2 f2 h

……………

g1

g2 ……………

……………

Доказательство Th.3.2.4

Любая h P2 представима h = fi (F1, F2, … , Fni) – формула над Σ* Здесь: F1, F2, … , Fni – подформулы также над Σ* (по условию)

Далее: Индукция по глубине формулы h = fi (F1, F2, … , Fni)

По условию: любая fi Σ* представима формулой над Σ:

f1 = gk1(g1, g2, … )

…………………………………..

fi = gki (g1, g2, … )

…………………………………..

gki (g1, g2, … ) – представление функции h формулой над Σ, т.е. для глубины = 1 доказано

Пусть верно для формул глубины k, т.е. все функции, представимые над Σ* формулами глубиной не более k, могут быть реализованы формулами над Σ

т.е. подпадают под индукционное предположение:

h = fi (gj1 (g1, g2, … ), gj2 (g1, g2, … ), … , gjni (g1, g2, … )) = = gki (gj1 (g1, g2, … ), gj2 (g1, g2, … ), … , gjni (g1, g2, … )) ( )

( ) - представление функции h формулой над Σ

В силу произвольности h P2 Доказано Th.3.2.4

……………

g1

g2 f2 h

……………

g1

g2 ……………

……………

Пример

Σ0 = { &, , - функционально полная (Th.3.2.1)

Доказать полноту системы Σ1 = { &,

1. Выбираем одну из известных полных систем в качестве Σ* (пока это только Σ0)

( (x y)) = ( x & y)

xy = ( x & y)

xy = Ф2(&, ) = ( x & y)

Эффективность более удачного выбора Σ*

Доказываем полноту Σ3 = { &, , 1 Кандидаты в Σ*: Σ0 = { &, , и Σ1 = { &,

Если выберем Σ0 в качестве Σ*, то представляем три функции системы Σ0 = { &, , формулами над Σ3 = { &, , 1 :

1) x & y = x & y 2) x = x 1

3) x y = x y = ( x & y) = ((x 1) & (y 1)) 1

Если выберем Σ1 в качестве Σ*, то представляем лишь две функции из Σ1 = { &, формулами над Σ3 = { &, , 1 :

Построить представление: x y = (&, , )

изменить на противоположное значение в последней строке. Это быть, например, функция F(x,y) = (x&y) или,

с учётом правил де Моргана (3.2.8), F(x,y) = x y.

Таким образом, получаем x y = (x y) & ( x y) =

[ (3.2.3) – дистрибутивность конъюнкции относительно дизъюнкции ] = (x& x) (x& y) (y& x) (y& y) =

[ (3.2.9) – закон противоречия, затем (3.2.7) – свойства констант ] = 0 (x& y) ( x&y) 0 = (x& y) ( x&y)