
Лекция дискрет 14
.pdf
Исчисление высказываний L – аксиомы:
|
Для любых формул A , B и C теории L |
|
следующие выражения – аксиомы: |
(А1) |
A ( B A ) |
(А2) |
(A (B C)) ((A B ) (A C )) |
(А3) |
( ┐B ┐A ) ( ( ┐B A ) B ) |
В исчислении L заданы не аксиомы, а схемы аксиом, из которых с использованием правила подстановки получаются частные случаи аксиом, например:
(А1) ┐A ((C D) ┐A)
(А2) (A (A A)) ((A A ) (A A))
(А3) ( ┐B ┐(A D)) (( ┐B (A D)) B)
Правило подстановки формулы вместо пропозициональной буквы (ср. § 3.3)
При подстановке формулы B1 в формулу B
вместо пропозициональной буквы Х должны быть одновременно заменены формулой B1
все вхождения пропозициональной буквы Х в формулу B

Исчисление высказываний L – правило вывода
Modus Ponens (MP):
A , A B
B
AB A B
Если ночное небо в звёздах, будет холодно
Небо - звёздное Значит, будет холодно
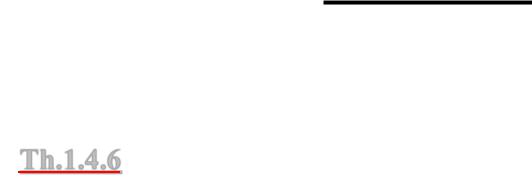
Исчисление высказываний L – правило вывода Modus Ponens
A , A B
B
Правило Modus Ponens (MP) – удаление импликации
Th.1.4.6 Любое бесконечное подмножество N N счётно
A B Если подмножество N N бесконечно, то оно счётно
A
B
1 N = F = { a0=a1=1; an = an-1 + an-2 (n≥2) } N бесконечно Применяем правило Modus Ponens, получим:
1 N = F = { a0=a1=1; an = an-1 + an-2 (n≥2) } N счётно

3) Свойства исчисления высказываний L
Вывод формулы B из формул
A 1 ,A 2 , … ,A n в аксиоматической теории Т
Последовательность формул F 1 ,F 2 , … ,F m такая что:
(1) F m есть B
(2) любая F i (i = 1 ….. m):
либо одна из аксиом теории Т
либо одна из исходных формул A 1 ,A 2 , … ,A n
либо непосредственно выводима из F 1 ,F 2 , … ,F i – 1
по одному из правил вывода теории Т

Общая идеология построения вывода
A 1 ,A 2 , … ,A n ├ B
в аксиоматической теории
Исходные формулы A 1 ,A 2 , … ,A n
(возможно, пустое множество)
+
Прототип(ы) – частный(е) случай(и) аксиом или формул, полученных ранее в результате доказательства утверждений и решения задач
+
Правила и квазиправила – приёмы для последовательного преобразования исходных и промежуточных формул к необходимому виду
Формулы теории L, которые могут быть приняты в качестве прототипов
|
(первоначальное множество, |
|
на основе определения L) |
(А1) |
A ( B A ) |
(А2) |
(A (B C )) ((A B ) (A C )) |
(А3) |
( ┐B ┐A ) ( ( ┐B A ) B ) |
|
Правила и квазиправила теории L |
|
|
(на основе определения L) |
|
1 |
Подстановка – одновременная замена в формуле F всех |
|
вхождений пропозициональной буквы, напр., А, на одну |
||
|
||
|
и ту же произвольную формулу, напр. , H |
|
2 |
Правила сокращения – представление логических связок |
&, , ≡ примитивными связками ┐и :
(D1) A & B означает ┐(A ┐B ) (D2) A B означает ┐A B
(D3) A ≡ B означает (A B ) & (B A )
3 |
Modus Ponens – удаление импликации: из посылок A и |
|
A B непосредственно выводима формула B
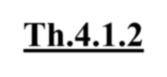
А2 (A (B C )) ((A B ) (A C ))
Th.4.1.2 Для любой формулыA исчисления L имеет место├ A A
1. (A ((A A ) A )) ((A (A A )) (A A )) A2
2. A ((A A ) A ) |
A1 |
|
3. |
(A (A A )) (A A ) |
МР к 1,2 |
4. |
A (A A ) |
А1 |
5. |
A A |
МР к 3,4 |
|
|
|
Утверждение типа «Если множество бесконечно, то оно бесконечно» не требует никаких аргументов в своё обоснование
