
Лекция дискрет 14
.pdf
Вывод формулы B из формул
A 1 ,A 2 , … ,A n в аксиоматической теории Т
Последовательность формул F 1 ,F 2 , … ,F m такая что:
(1) F m есть B
(2) любая F i (i = 1 ….. m):
либо одна из аксиом теории Т
либо одна из исходных формул A 1 ,A 2 , … ,A n
либо непосредственно выводима из F 1 ,F 2 , … ,F i – 1
по одному из правил вывода теории Т
Обозначение: A 1 ,A 2 , … ,A n ├ B
A 1 ,A 2 , … ,A n – посылки или гипотезы вывода
B - формула, выводимая из посылок A 1 ,A 2 , … ,A n
Теоремы и доказательства формул аксиоматической теории
Доказательством формулы B в аксиоматической теории Т, называется вывод формулы B из пустого множества посылок (гипотез), т.е. ├ B
Формула, для которой существует доказательство в аксиоматической теории Т, называется доказуемой в теории Т или теоремой теории Т

Th.4.1.1: и Γ – множества формул теории Т, A и B -
формулы теории Т
(1)Если Γ и ├ A , то имеет место вывод Γ├ A
Доказательство По определению вывода A 1 , … ,A n├ A не требуется использовать все посылки A 1 , … ,A n
!Возможность расширения множества посылок вывода
Теорема Пифагора: Если треугольник ABC со сторонами a, b и c – прямоугольный, то a2 + b2 = c2
Расширение множества условий теоремы Пифагора: Если треугольникABC со сторонами a, b и c – прямоугольный, пушистый и покрашен в зелёный цвет, то a2 + b2 = c2
Здесь: = { треугольник ABC со сторонами a, b и c: (1) прямоугольный }
Γ = { треугольник ABC со сторонами a, b и c: (1) прямоугольный, (2) пушистый, (3) покрашен в зелёный цвет }

Th.4.1.1: и Γ – множества формул теории Т, A и B -
формулы теории Т
(2)Γ├ A тогда и только тогда, когда в Γ существует конечное подмножество такое, что ├ A
Доказательство
( ) Если существует конечное Γ такое, что ├ A , то, применяя Th.4.1.1(1), получим Γ├ A
( ) По определению, вывод – конечная последовательность формул, значит, в нём может быть использовано лишь конечное множество посылок
!Конечность используемого в выводе множества посылок

Th.4.1.1: и Γ – множества формул теории Т, A и B - формулы теории Т
(3) Если ├ A и для любого B Γ ├ B , то Γ├ A
Доказательство
В выводе ├ A вместо каждой из посылок B
подставим её вывод Γ ├ B , получим вывод Γ├ A
!Транзитивностьформул свойства выводимости
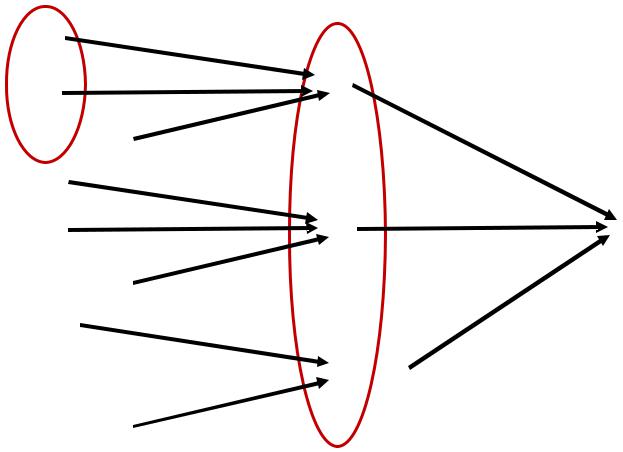
Множество |
Множество |
формул Γ Γ ├ B формул |
|
G1 |
|
G2 |
B1 |
……………
G1
G2 |
B2 |
……………
G1
G2  ……………
……………
……………
├ A
A

2) Исчисление высказываний L Исчисление высказываний L – алфавит: а) пропозициональные буквы:
A, B, C, …………….. , X, Y, Z
б) знаки логических связок:
┐, (примитивные), &, , ≡, при этом
(D1) A & B означает ┐(A ┐B ) (D2) A B означает ┐A B
(D3) A ≡ B означает (A B ) & (B A )
в) скобки ( )

Назначение символов алфавита исчисления L
Пропозициональные Простые (неделимые) переменные буквы утверждения
Логическая связка ┐А Составное утверждение «Неверно, что имеет место А»
Логическая связка А В Составное утверждение «Если А, то В»
Логическая связка А & В Составное утверждение «Имеют место оба утверждения А и В»
Логическая связка А В Составное утверждение «Имеет место хотя бы одно из утверждений А и В»
Логическая связка А В Составное утверждение «А и В – равносильные утверждения»
Круглые скобки ( ) Указание необходимого порядка применения логических связок

Значение пропозициональных букв и результатов применения примитивных логических связок исчисления L
Значения
пропозициональных |
false |
true |
букв |
|
|
Связка ┐ |
┐ false = true |
┐ true = false |
A |
B |
A B |
false |
false |
true |
false |
true |
true |
true |
false |
false |
true |
true |
true |

Исчисление высказываний L – формулы:
а) любая пропозициональная буква
A, B, C, ………, X, Y, Z есть формула
б) если A и B - формулы, то следующие выражения
есть формулы:
(┐A ) (A B )
в) выражения, не подпадающие под а) или б) – не формулы исчисления L
Выражение является формулой L
(A (┐B ┐C )) ((A B ) ┐(A C ))
Выражение не является формулой L
(A ( ┐B ┐C )) ((A B ) ┐ (A C ))
