
Signaly_1
.pdf
51
Тогда модель идеальной последовательности δ-функций (δ T (t )) можно описать
следующим выражением
+¥ |
|
δ T (t ) = ∑δ (t - n ×T ), |
(2.83) |
n=-¥
авыходной сигнал x* (t ), который представляет собой последовательность идеальных
импульсов, амплитуды которых соответствуют последовательности мгновенных значений входного сигнала ( x(0), x(T ) , x(2T ) и т.д.) может быть записан в следующем виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
x* (t ) = δ T (t )× x(t ). |
|
|
|
|
(2.84) |
|||||||
|
|
|
Последовательность дискретных значений сигнала |
x(kT ) , |
как показано ранее, |
||||||||||||||||||||
может быть представленаследующимвыражением: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(kT ) = ∫ x(t )×δ (t - kT )dt . |
|
|
|
(2.85) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как функция последовательности идеальных импульсов δ T (t ) периодическая, |
||||||||||||||||||||||
то она может быть разложена в ряд Фурье |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ T (t ) = ∑ |
|
|
n |
× e j×n×ωu ×t |
, |
|
|
|
(2.86) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n=-¥ |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
(t )× e- j×n×ωu ×t dt , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
∫δ T |
|
|
|
|
|
|
|
|
|
|
|
|
(2.87) |
||||||||||
где |
C |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
T |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
-T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωu |
= 2π × fu |
= |
2π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = |
|
∫δ T (t )× e- j×n×ωu ×t dt = |
∫δ |
(t )dt = |
, |
|
(2.88) |
||||||||
|
|
|
|
|
|
|
|
C |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
T |
T |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
-T |
|
-0 |
|
T |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
то можнонаписать |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
δ T (t ) = |
1 |
|
+¥ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑e j×n×ωu ×t . |
|
|
|
(2.89) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T n=-¥ |
|
|
|
|
|
|
||||
|
|
|
Таким образом, спектр идеальной последовательности δ-функции состоит из |
||||||||||||||||||||||
бесконечного числа гармоник с одинаковой |
амплитудой |
1 |
. И |
сигнал на выходе |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
импульсного модулятора x* (t ) можно найти из соотношения: |
|
|
|
|
|||||||||||||||||||||
52
|
1 |
+¥ |
|
|
|
x* (t ) = |
∑ x(t )× e j×n×ωu |
×t . |
(2.90) |
||
|
|||||
|
T n=-¥ |
|
|
||
§2.11. Влияниеимпульсного модулятора на спектр входного сигнала
При импульсных видах модуляции, и, в частности, при цифровой модуляции, которая используется при цифровой обработке сигналов, происходит преобразование входного сигнала в импульсную форму. Импульсные сигналы имеют довольно сложный спектр, который изменяет спектр входного сигнала. Важно выяснить закономерности изменений спектров непрерывных сигналов при прохождении ими импульсных модуляторов. Рассмотрим модель прохождения непрерывного сигнала x(t ) через импульсный модулятор, представленную на рис.2.7, в которой в качестве последовательностей импульсов используется идеальная последовательность δ-функции. Если на входе импульсного модулятора действует гармонический сигнал с частотой ω0 и амплитудой A, то есть
x(t ) = A cosω0t = |
A0 |
(e j×ω0 ×t + e - j×ω0 ×t ), |
(2.91) |
|
|||
2 |
|
|
|
то спектр сигнала на выходе импульсного модулятора будет состоять из частот, отличающихся от частоты ω0 на целое число частот прерывания ωu . Действительно, в соответствии с (2.90)
x* (t ) = |
A |
∑+¥ [e j×(ω0 +nωu )×t + e- j×(ω0 -nωu )×t ]= |
A |
(e j×ω0 ×t + e- j×ω0 ×t )+ |
|
|||||||
|
|
|
||||||||||
|
|
|
|
|
2T n=-¥ |
|
2T |
|
||||
+ |
|
A |
∑+¥ [e j×(ω0 +nωu )×t + e- j×(ω0 -nωu )×t + e j×(ω0 -nωu )×t + e- j×(ω0 +nωu )×t ]= |
(2.92) |
||||||||
|
2T |
|||||||||||
|
|
n=1 |
|
|
|
|
|
|
||||
|
|
A |
|
|
|
|
+¥ |
|
|
|
|
|
= |
cosω 0t + |
∑[cos(ω0 + nωu )t + cos(ω 0 |
- nωu )t]. |
|
||||||||
|
|
|||||||||||
|
|
T |
|
|
|
n=1 |
|
|
|
|
|
|
Таким |
|
образом, |
вследствие |
воздействия |
импульсного элемента на |
входной |
||||||
гармонический сигнал в частном спектре выходного сигнала появляется бесконечное количество высокочастотных составляющих с частотами (ω0 ± nωu ) , называемых боковыми частотами. Дополнительные высокочастотные гармоники имеют те же амплитуды, что и основная частота и частоты их сдвинуты на величину nωu . На рис.2.8а представлен спектр входного гармонического сигнала x(t ), а на рис.2.8б - частотный спектр выходного сигнала x* (t ).

|
|
53 |
|
|
|
|
|
|
|
|
|
x(ω) |
|
|
|
|
|
|
x (ω) |
|
|
|
|
|
-2ωu |
-ωu |
|
|
|
|
ωu |
|
2ωu |
|
|
|
|
|
|
|
|
|
|||||
|
-2ωu-ω0 |
|
|
|
|
|
|
|
|
||
|
-ωu-ω0 |
|
|
|
|
|
ωu+ω0 |
|
|
||
-ω0 ω0 ω |
|
-ω |
|
ω |
|
ω |
|||||
-2ωu+ω0 -ωu+ω0 |
0 |
0 |
0 |
ωu-ω0 |
2ωu-ω20 ωu+ω0 |
|
|||||
а) |
|
|
|
|
|
б) |
|
|
|
|
|
Рис.2.8
В случае, если на входе импульсного модулятора действует периодическая функция,
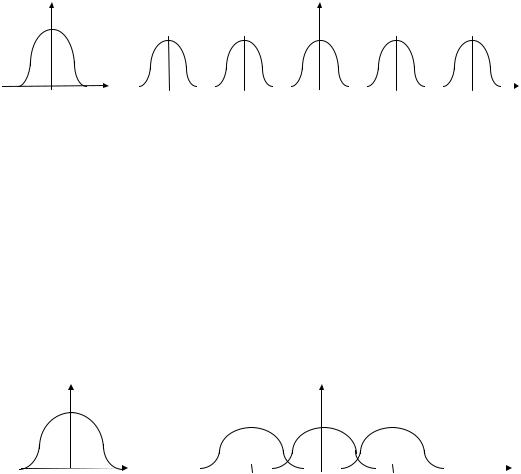
которая, следовательно, имеет линейчатый спектр, то частотный спектр на выходе легко определяется из соотношения (2.91) и (2.92), если его применить для основной частоты и каждой из гармоник. На рис.2.9а изображен частотный спектр периодического сигнала x(t ), а на рис.2.9б - частотный спектр сигнала x (t ), полученного после прохождения сигнала x(t )
через импульсный модулятор.
x(ω) |
x (ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-ω0 |
ω0 ω -ωu- -ωu -ωu+ω0 |
-ω0 0 ω0 |
ωu-ω0 ω |
u ωu+ω0 ω |
||||||||||||||||||||||||||
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
||||||
Рис.2.9
Таким образом, если входной периодический сигнал состоит из n частотных составляющих, лежащих в диапазоне от 0 до ω0 (графически частотный спектр в этом случае изображается n вертикальными линиями, высота каждой из которых равна амплитуде частотной составляющей), то в результате влияния импульсного модулятора частотный спектр выходного сигнала будет содержать бесконечное количество высокочастотных составляющих,
сгруппированных в группы по n гармоник и отстоящих от соответствующих частотных составляющих на величину ± nωu . Графически это изобразится как бесконечное повторение частотного спектра входного сигнала вдоль оси ω через промежуток ωu (рис.2.9б). Если на входе импульсного модулятора действует непериодический сигнал, имеющий непрерывный
54
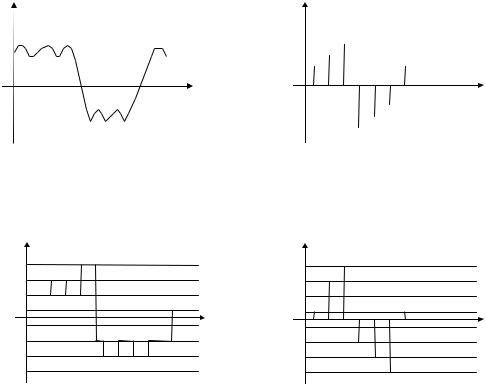
спектр, состоящий из бесконечного числа частотных составляющих, лежащих в диапазоне от 0
до ω0 , то частотный спектр выходного сигнала может быть найден из соотношения (2.91) и (2.92) аналогично тому, как был найден спектр выходного сигнала в случае поступления на вход импульсного модулятора периодического сигнала с учетом того, что число частотных составляющих бесконечно. На рис.2.10а представлен частотный спектр непериодического сигнала x(t ), а на рис.2.10б частотный спектр сигнала x (t ), полученного после прохождения сигнала x(t ) через импульсный модулятор.
x(ω) |
x (ω) |
|
|
|
|
|
|
|
|
|
ω |
-ω0 |
ω0 ω |
-2ωu |
-ωu |
-ω0 |
ω0 |
ωu-ω0 |
ωu |
2ωu-ω0 |
2ωu+ω0 |
|
а) |
|
-ωu-ω0 |
-ωu+ω0 |
0 |
|
ωu+ω0 2ωu |
||
|
|
|
|
б) |
|
|
|
|
|
Рис.2.10
Во всех рассмотренных случаях входной сигнал может быть выделен из выходного сигнала путем частотной фильтрации только тогда, когда ωu (частота прерывания импульсного
модулятора) не менее чем в 2 раза превышает ω0 (ω0 - верхняя граница входного сигнала).
Это следует из теоремы Котельникова. Если это условие не выполняется (то есть
ωu < 2ω0 ), то исходный сигнал x(t ) не может быть выделен из выходного сигнала x (t ).
x(ω) x (ω)
ω |
-ωu |
ωu |
ω |
а) |
|
б) |
|
Рис.2.11
Действительно, как видно из рис.2.11, на котором представлен частотный спектр входного сигнала x(t ) (рис.2.11а) и частотный спектр выходного сигнала x (t ) (рис.2.11б)
для случая, когда ωu < 2ω0 , в частотном спектре выходного сигнала x (t ) происходит
55
наложение частот, что искажает частотный спектр, соответствующий входному сигналу, и
ведет к невозможности выделения исходного сигнала путем частотной фильтрации.
§2.12. Случайные сигналы
Как указывалось ранее, детерминированный сигнал не может использоваться для передачи информации, так как получение информации основано на устранении априорной неопределенности состояний источника сообщений. Следовательно, детерминированный сигнал только тогда будет нести информацию, если он по некоторому закону распределения выбирается из множества возможных сигналов. Поэтому в качестве моделей сигналов необходимо использовать случайные функции (случайные процессы, если они зависят от времени).
Случайными функциями называют функции, которые в результате эксперимента могут принимать тот или иной конкретный вид, неизвестный заранее. Конкретный вид, принимаемый случайной функцией в результате эксперимента, называют реализацией этой функции.
Несколько реализаций одной и той же случайной функции называют ансамблем или семейством реализаций этой функции.
Случайные функции, зависящие от нескольких аргументов, называют случайными полями. Случайные функции широко используются при моделировании различных объектов и процессов. При исследовании природных ресурсов примерами таких функций могут быть функции, ставящие в соответствии с координатами исследуемого участка поверхности значения яркости, или давления, или температуры и т.п. Как случайную функцию можно рассматриватьпрофиль рельефа исследуемого участка поверхности.
Примерами случайных функций, зависящих от времени, которые называют случайными процессами, могут быть изменение температуры в данной точке с течением времени, внешние воздействия на летательный аппарат во время его полета и т.п.
Реальные детерминированные сигналы всегда содержат некоторые случайные составляющие, вызванные помехами, которые искажают форму сигнала. Математическая модель помехи так же может быть представлена в виде случайного процесса с определенными параметрами.
Статистические свойства помехи и сигнала, как правило, различны, что позволяет производить их разделение.
56
Рассмотрим некоторую случайную функцию X (t ). Предположим, что в результате n
независимых экспериментов получено n реализаций этой функции: x1 (t ), x2 (t ),..., xn (t ) .
Каждая реализация представляет собой обычную неслучайную функцию. Если зафиксировать некоторое значение аргумента t = t0 , то X (t0 ) будет представлять собой случайную величину. Эту случайную величину называют сечением случайной функции,
соответствующим данному значению аргумента t0 . В данном сечении получим n значений,
принятых случайной величиной в экспериментах. Основными характеристиками, по которым можно провести классификацию случайных функций, является пространство состояний и статистическиехарактеристики.
Пространством состояний называют множество возможных значений случайной
величины X (t0 ).
Случайная функция, у которой пространство состояний представляет собой бесконечное множество значений, принадлежащих некоторому отрезку (континуим), а
изменение состояний возможно при любом значении аргумента, называют непрерывной случайной функцией. Если же изменение состояний допускается лишь в конечном числе значений аргумента, то говорят о непрерывной случайнойпоследовательности.
Случайная функция, принимающая конечное число различных значений и состояние которой может изменяться при любом значении аргумента, называется дискретной случайной функцией. Если же изменения состояний возможны только в конечном или счетном числе значений аргумента, то говорят одискретных случайных последовательностях.
Иллюстрация реализаций указанных классов случайных функций представлена на рис.2.12, где
57
а) |
x(t) |
б) |
x(t) |
t |
t |
а - непрерывная случайная функция; |
|
б - непрерывная случайная |
||||||||
|
|
|
|
|
|
|
|
|
|
последовательность; |
в) |
x(t) |
г) |
x(t) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
t |
в - дискретная случайная функция; |
г - дискретная случайная |
|
последовательность. |
|
Рис. 2.12 |
В соответствии с определением случайной функции и ее сечения любая
случайная функция X (t) может быть описана совокупностью n зависимых случайных
величин, соответствующих ее сечениям при значении аргумента t1 , t2 ,..., tn : |
|
X 1 = X (t1 ), X 2 = X (t2 ),…, X n = X (tn ) . |
(2.93) |
При n → ∞ , такая совокупность эквивалентна случайной функции X (t). |
|
Исчерпывающей характеристикой такой совокупности будет n-мерная плотность вероятности. Однако вычисление ее при больших n чрезвычайно затруднено,
поэтому на практике ограничиваются одно или двумерной плотностью вероятности.
Одномерная плотность распределения вероятности p1 (X i , t1 ) случайной
функции X (t) представляет собой закон распределения случайной величины X1 ,
соответствующей сечению случайной функции X (t) при значении аргумента равном t1 .
58
Двумерная плотность вероятности p2 (X 1 , X 2 , t1 , t2 ) характеризует вероятность
совместной реализации любых двух значений случайных величин X1 и X 2 ,
соответствующих сечениям случайной функции при значениях аргумента t1 и t2
соответственно. Двумерная плотность вероятности позволяет оценить скорость изменения случайной функции.
Практическое нахождение функций плотности вероятности даже низших порядков довольно трудоемко, поэтому в большинстве случаев ограничиваются определением простейших характеристик случайных функций, аналогичных числовым
(статистическим) характеристикам случайных величин.
Действительно, так как каждое сечение случайной функции представляет собой случайную величину, то охарактеризовать все возможные реализации данной случайной функции можно с помощью числовых характеристик, используемых для случайных величин: математического ожидания ( m x ) и дисперсии ( Dx ). Тогда для
сечения t = t1
+∞ |
|
|
|
|
|
|
|
|
m x (t1 ) = M {X (t1 )}= ∫ X 1 × p1 |
(X 1 ; t1 )dx ; |
|
|
|
|
|
(2.94) |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Dx (t1 ) = D{X (t1 )}= M {(X (t1 ) - mx (t1 ))2 }= M X (t1 ) |
, |
(2.95) |
||||||
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где M - оператор математического ожидания; |
|
|
|
|
|
|
|
|
D - оператор дисперсии; |
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
X (t1 ) = X (t1 ) - mx (t1 ) - центрированная случайная величина. |
|
|
|
|
|
|
|
|
Откуда при произвольном значении t |
|
|
|
|
|
|
|
|
m x (t) = M {X (t )}, |
|
|
|
|
|
|
|
(2.96) |
|
|
|
|
2 |
|
|
|
|
Dx (t) = D{X (t)}= M {(X (t) - m x (t))2 }= M X (t ) |
. |
|
(2.97) |
|||||
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математическим ожиданием случайной функции X (t) называется неслучайная функция mx (t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.
Дисперсией случайной функции X (t ) называется неслучайная функция D(t),
значение которой для каждого t равно дисперсии соответствующего сечения случайной функции. Математическое ожидание случайной функции представляет собой
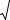
59
некоторую среднюю функцию, около которой различным образом варьируются конкретные реализации случайной функции, а дисперсия случайной функции характеризует разброс возможных реализаций случайной функции относительно этой средней функции. На практике вместо дисперсии часто используют производную от нее функцию σ x (t):
σ x (t) = |
|
, |
|
Dx (t) |
(2.98) |
которую называют средним квадратическим отклонением. Преимущества ее использования основаны на том, что ее размерность совпадает с размерностью случайных функций и случайных величин.
Следует отметить, что математическое ожидание и дисперсия случайной функции не позволяет получить представление о конкретном виде ее реализации, так как не позволяют оценить скорость ее изменения при изменении параметра. Чтобы охарактеризовать случайную функцию надо показать степень статистической
зависимости между собой значений случайных величин и
представляющих собой сечения случайной функции при двух различных значениях аргумента t.
Степень зависимости двух случайных величин (X и Y) определяют их
корреляционным моментом K xy , который иногда называют ковариацией. Как известно,
K x, y |
= M {(X - mx |
)(Y - m y |
|
O |
O |
(2.99) |
)}= M X ×Y . |
||||||
|
|
|
|
|
|
|
Для дискретных случайных величин X ,Y корреляционный момент находится по формуле:
|
K xy = ∑∑(xi - mx )(y j - m y )pij , |
(2.100) |
|
|
i |
j |
|
где xi , y j - значения, которые могут принимать случайные величины X ,Y ; |
|
||
mx |
и my - математические ожидания этих случайных величин; |
|
|
pij |
- вероятность того, что X примет значение xi , а Y - y j . |
|
|
|
Для непрерывных случайных величин ковариация (корреляционный момент) |
||
находится по формуле: |
|
|
|
|
+∞ +∞ |
(x - m x )(y - m y )p(x, y)dxdy , |
|
|
K xy = ∫ ∫ |
(2.101) |
|
−∞−∞
60
где p(x, y) - плотность распределения непрерывных случайных величин |
X ,Y , а m x и |
||||
m y - их математические ожидания. |
|
|
|
|
|
С помощью корреляционного момента можно найти ρ xy - |
коэффициент |
||||
корреляции случайных величин X и Y: |
|
|
|
|
|
ρ xy = |
|
K xy |
, |
(2.102) |
|
σ xσ y |
|||||
|
|
|
|||
где σ x и σ y - средние квадратические отклонения величин X и Y. |
|
||||
Как известно, |
|
|
|
|
|
− 1 ≤ ρ xy |
≤ 1 . |
|
(2.103) |
||
Случайные величины, для которых Kxy = 0 , называются некоррелированными. В
соответствии с (2.102) для таких случайных величин также и коэффициент корреляции
ρ xy = 0 .
Для случайных функций вводится понятие корреляционной функции.
Корреляционной функцией случайной функции X (t) называется неслучайная функция
двух аргументов K x (t1 , t2 ), которая при каждой паре значений t1 ,t2 |
равна |
корреляционному моменту соответствующих значений случайной функции: |
|
K x (t1 , t2 ) = M {(X (t1 ) − mx (t1 ))(X (t2 ) − mx (t2 ))}. |
(2.104) |
Корреляционная функция используется для определения статистических связей как между отдельными сечениями одной случайной функции, так и между двумя различными функциями. В первом случае она часто называется автокорреляционной, а
во втором - взаимнокорреляционной.
Как следует из (2.104) автокорреляционная функция не зависит от порядка своих аргументов:
K x (t1 , t2 ) = K (t2 , t1 ) . |
(2.105) |
Если t2 = t2 = t , то |
|
K x (t, t) = M {(X (t) − mx (t))2 }= Dx (t) , |
(2.106) |
то есть при t1 = t2 автокорреляционная функция обращается в дисперсию случайной
функции.
§2.13. Стационарные случайные функции
