Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет геодезии и картографии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Signaly_1

.pdf

Скачиваний:

Добавлен:

10.03.2016

Размер:

761.84 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

+¥

B(ω ) = ∫ S (t)×sin ω tdt - мнимая часть S (iω );

-¥

S (ω ) = 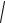[A(ω )]2 + [B(ω )]2 - модуль S (iω ) или спектр непериодического сигнала;

Y(ω ) = arctg B(ω ) - фаза S (iω ).

A(ω )

Так как A(ω ) - четная функция частоты, а B(ω ) - нечетная относительно частоты

ω , то, как и в случае ряда Фурье, модуль спектральной плотности (S (ω )) - есть функция четная, а фаза Y(ω ) - нечетная относительно частоты.

Обратное преобразование Фурье так же легко привести к тригонометрической форме. Действительно в соответствии с (2.30) и учетом (2.43) имеем:

			1	+¥			1	+¥
U (t) =				∫		(iω )× eiωt dω =		∫ S (ω )× ei[ω×t-ψ (ω )]dω =
					S
			2π		S		2π
			2π	-¥			2π	-¥			(2.47)
				-¥				-¥
1		+¥								+¥
		+¥								+¥
		∫ S (ω )× cos[ω × t -ψ (ω )]dω +							i	∫ S(ω )× sin[ω × t -ψ (ω )]dω.
	2π	∫ S (ω )× cos[ω × t -ψ (ω )]dω +							2π	∫ S(ω )× sin[ω × t -ψ (ω )]dω.
	2π	-¥							2π	-¥
		-¥								-¥

Второе слагаемое из-за нечетности подинтегрального выражения равно нулю,

следовательно:

	1	+¥	1	+¥
U (t ) =		∫ S (ω )× cos[ω × t -ψ (ω )]dω =		∫ S (ω )× cos[ω × t -ψ (ω )]dω . (2.48)
	2π		π
		- ¥		0

Преимуществом тригонометрической формы записи преобразования Фурье является его более простое и удобное физическое толкование.

§2.7. Основные свойства преобразования Фурье

1.Свойство линейности.

Если S1 (ω ) - спектральная плотность сигнала s1 (t), а S2 (ω ) - сигнала s2 (t), то при любых произвольных постоянных a1 и a2 спектральная плотность сигнала

S(t ) = a1s1 (t ) + a2 s2 (t)

будет равна
S(ω ) = a1S1 (ω ) + a2 S2 (ω ),	(2.49)

что следует из линейности операции интегрирования. 2.Свойство симметрии.

Если сигнал s(t ) имеет спектральную плотность	S (ω ) , то спектральная
плотность сигнала S (t ) будет 2 ×π × s(- ω ).
Действительно, как следует из (2.39) при t = −t
+¥
2π × s(- t) = ∫ S (ω )× e-i×ω×t dω .	(2.50)

-¥

Приведем в этом равенстве последовательно ряд замен переменных:

		+¥
	2π × s(- t )	= ∫ S (ω )× e-i×x×t dx ;
		-¥
		+¥
	2π × s(- ω )	= ∫ S (x)× e-i×x×ω dx ;
		-¥
	+¥
	2π × S (- ω ) = ∫ S (t )× e -i×t×ω dt = S [S (t )].
	-¥
Следовательно, спектральная плотность сигнала S(t ) равна 2π × s(- ω ). Если s(t )
- четная функция,	то s(- ω ) = s(ω ) и	спектральная плотность	сигнала	S(t ) равна
2π × s(ω ).
3. Свойство изменения масштаба.
Если сигнал	s(t ) имеет спектральную плотность S(ω ),		то при	изменении

масштаба исходного сигнала, то есть для сигнала s(a ×t ) ( a -любая действительная постоянная) спектральная плотность равна

1		ω
	× S	.
a
	a

Действительно:

+¥

S[s(a × t )] = ∫ s(a × t)× e-i×ω×t dt .

-¥

Произведем замену переменных a ×t = x , тогда а) при a > 0

S[s(at)] =	1		+¥	-iω x		1			ω
			∫ s(x)× e a		dx =			S		;
	a		∫ s(x)× e a		dx =	a		S		;
	a		-¥			a			a
			-¥
б) при a < 0
S[s(at)] = -	1		+¥	-iω x			1			ω
			∫ s(x)× e a		dx = -				S	.
		a	∫ s(x)× e a		dx = -			a	S	.
		a	-¥					a	a
			-¥

(2.51)

(2.52)

43
	1			ω
Следовательно, спектральная плотность сигнала	s(a ×t ) равна		S	.
Следовательно, спектральная плотность сигнала	s(a ×t ) равна		S	.
		a	a

4. Свойство частотного сдвига. Если S(ω ) спектральная плотность сигнала s(t ),

то сигналу s(t )×eiω0t соответствует спектральная плотность S(ω - ω0 ), то есть

умножение сигнала s(t ) на eiω0t сдвигает весь спектр S(ω ) на частоту ω0 .

Для доказательства этого свойства применим обратное преобразование Фурье к

спектру S(ω - ω0 ) и произведем замену переменных ω - ω0						= x , тогда
1		+¥S(ω - ω0 )× eiω0t dω =		1	+¥S(x)× ei×x×t × ei×x0 ×t dx = s(t)× ei×ω0 ×t .		(2.53)
	2π			2π
		∫			∫
		-¥			-¥
Таким образом, сигналу			s(t )×eiω0t		соответствует	спектральная	плотность

S(ω - ω0 ).

5. Свойство временного сдвига.

Если S(ω ) есть спектральная плотность сигнала s(t ), то сигналу s(t - t0 )

соответствует спектральная плотность S(ω )× e-iωt0 . Для доказательства этого свойства применим прямое преобразование Фурье к сигналу s(t - t0 ) и сделаем в нем замену переменных t - t0 = x , тогда

∫ s(t - t0 )×e-iω×t dt =

-¥

∫ s(x)

-¥

× -iω (x+t ) = -iωt × ∫ × -iω×x = ω × -iω ×t

e 0 dt e 0 s(x) e dx S ( ) e 0 . (2.54)

-¥

	Таким					образом,				сигналу			s(t - t0 )				соответствует				спектральная плотность
S(ω )× e-iωt0 .				Другими словами,								при сдвиге сигнала на t0 , его амплитудный спектр не
меняется, а изменяется только фазовый спектр на величину - ω × t0 .
	6. Если сигнал s1 (t) имеет спектральную плотность S1 (ω ), а сигнал s2 (t ) - S2 (ω ),
то
	¥ s (t)× s (t)dt =								1	¥ s (t)dt ¥ S (ω )× eiω×t dω =								1	¥	S (ω )dω ¥ s (t )× eiω×t dt =
	¥ s (t)× s (t)dt =								2π	¥ s (t)dt ¥ S (ω )× eiω×t dω =								×π	∫	S (ω )dω ¥ s (t )× eiω×t dt =
	∫	1				2			2π	∫	1	∫	2				2	×π	∫	2	∫	1
		1				2					1		2							2		1
	-¥									-¥		-¥							-¥		-¥		(2.55)
			1		¥			(ω )× S (- ω )dω =					1	¥		(ω )× S * (ω )dω,							(2.55)
	=				¥									¥
						S								S
		2	×π			S							×π	S
		2	×π		-∫¥		2	1				2	×π	-∫¥	2		1
							2	1							2		1
где S	* (ω ) –			комплексно сопряженная с S (ω ) функция.
	1													1

7. Если сигнал s(t ) со спектральной плотностью S(ω ) проходит через некоторое звено с предаточной функцией W (p) , то спектральная плотность выходного сигнала

S'(ω ) равна
S'(ω ) = S(ω )×W (i ×ω ).	(2.56)

§2.8. Распределение энергии в спектре непериодического сигнала

Если задан непериодический сигнал s(t ), физическим представлением которого может быть электрическое напряжение на активном сопротивлении в 1 Ом, то можно найти количество энергии, выделяемое на этом сопротивлении за время действия сигнала:

+∞	(t)dt .
E = ∫ s 2	(t)dt .	(2.57)

−∞

Понятие энергии сигнала имеет смысл только в том случае, если интеграл (2.57)

конечен.

Сигналы с конечной энергией называют энергетическими. Если сигналу s(t )

соответствует спектральная плотность S(ω ), то используя обратное преобразование Фурье и, меняя порядок интегрирования, можно записать:

+∞

E = ∫ s 2

(t)dt = ∫ s(t)× s(t)dt = ∫ s

(t )×

∫

(ω )× eiωt dω dt =

2π

−∞

+∞

(ω )× [s(t )× eiωt dt]dω =

+∞

(ω )×

(- ω )dω.

∫

2π

−∞

Для действительной функции s(t )

S (- ω ) = S (ω ),

где S (- ω ) - комплексно-сопряженна S (ω ) функция, и поэтому

S (ω )× S (ω ) = S(ω ) 2 ,

причем, как указывалось ранее (§2.4), S (ω ) 2 - четная функция.

Таким образом,

+∞

E = ∫ s 2

(t )dt =

∫

S (ω )

2 dω =

∫

S (ω )

2 dω .

2π

−∞

(2.58)

(2.59)

S (ω ) 2 - называют спектром плотности энергии или спектральной плотностью энергии сигнала, физический смысл которого - энергия, приходящаяся на единицу полосы частот при текущей частоте ω (размерность: энергиягерц). Соотношение (2.59),

известное как равенство Парсеваля, показывает, что энергию, выделяемую непериодическим сигналом за время его действия, можно найти, интегрируя квадрат модуля его спектральной характеристики во всем интервале частот.

В отличие от формулы (2.33) формула (2.59) определяет не среднюю мощность,

которая для любого непериодического абсолютно интегрируемого сигнала равна 0 (так как T → ∞ ), а полную энергию, выделяемую сигналом s(t ) за все время его действия.

Спектральная плотность энергии, характеризующая распределение энергии по спектру сигнала, существует лишь для энергетически ограниченных сигналов (для которых выражение (2.57) конечно), к которым применимо преобразование Фурье.

Если же значение интеграла (2.57) бесконечно, то понятие энергии сигнала теряет смысл. В этом случае рассматривают среднюю мощность сигнала. Сигналы с ограниченной мощностью называют мощностными.

Определим среднюю мощность непериодического сигнала s(t ) как среднюю мощность W, рассеиваемую на активном сопротивлении величиной 1 Ом в течение времени

(Т) действия сигнала, тогда:

(t )dt .

W = lim

∫ s2

(2.60)

T →∞ T

−T

Непериодический сигнал s(t ) представим конечным по времени сигналом sT (t ):

s(t ), при

;

(t ) =

(2.61)

0, при

При конечном Т сигнал s(t )

имеет конечную энергию, и тогда, в соответствии (2.59),

энергия ET

сигнала sT (t ) определится из выражения:

+ ∞

ET =

∫ s2 (t )dt =

∫

ST (ω )

2 dω ,

(2.62)

2 ×π

−T

−∞

где ST (ω )

- спектральная плотность сигнала s(t ). Следовательно,

+∞

(ω )

W = lim

= lim

∫ s2 (t )dt =

∫ lim

dω .

(2.63)

2 ×π

T →∞ T

−T

−∞

Если предел под знаком интеграла существует, то эта функция называется

спектральной плотностью мощности (P(ω )), то есть

P(ω ) = lim

(ω )

(2.64)

T →∞

∞

Можно доказать, что

P(ω ) = 2 ×π ∑

2δ (ω - nω0 ) и

среднюю

мощность

n =−∞

сигнала W, с учетом четности функции P(ω ), можно представить в виде:

+∞

W =

∫ P(ω )dω =

∫ P(ω )dω .

(2.65)

2 ×π −∞

§2.9. Корреляционныефункциидетерминированных сигналов

С физической точки зрения корреляционная функция характеризует взаимосвязь или взаимозависимость двух мгновенных значений одного или двух различных сигналов в

моменты времени t1 и t2 = t1 +τ . В первом случае корреляционную функцию часто

называют автокорреляционной, а во втором - взаимнокорреляционной. Корреляционные

функции детерминированныхпроцессовзависяттолькоот τ = t2 - t1 .

Если заданы

сигналы s1(t )

и s2 (t ), то

корреляционные функции определяют

следующими выражениями:

Rs1s2 (τ ) =

∫ s1(t )× s2

(t + τ )dt

- взаимнокорреляционная функция;

(2.66)

−T

(τ ) =

∫ s(t )× s(t + τ )dt

- автокорреляционная функция.

(2.67)

−T

Если s1(t ) и

s2 (t ) - два периодических сигнала с одинаковым периодом T,

то

очевидно, что их корреляционная

функция Rs

, s

(τ ) тоже является периодической

периодом Т и, следовательно, она может быть разложена вряд Фурье.

Действительно, если в выражении (2.66) разложим в ряд Фурье сигнал s2 (t + τ ) , то получим

+¥

Rs1s2

(τ ) =

∫ s1 (t )× s2 (t + τ )dt =

∫ s1

(t )

× ∑

C2n × ei×n×ω 0 (t

+τ )dt =

n =-¥

(2.68)

+¥

i×n×ω 0 ×τ 1

∫ s1 (t )× e

i×n×ω

0 ×t

i×n×ω 0

×τ

= ∑C2n × e

∑C1n × C2n × e

n =-¥

-T 2

n =-¥

- комплексные амплитуды n-й гармоники сигналов s1(t ) и s2 (t )

где

C1n и C2n

соответственно,

комплексно-сопряженный

коэффициент.

Коэффициенты

разложения взаимно корреляционной функции (C*

× C

) можно найти как коэффициенты ряда

Фурье

(τ )× e-i×n×ω0 ×t dt .

C1*n

× C2n

∫ Rs1s2

(2.69)

-T

Частотное разложение автокорреляционной функции легко получить из формул (2.68) и

(2.69), положив s1 (t ) = s2 (t ) = s(t ), тогда

+¥

Rs (τ ) =

T∫

s(t )× s(t + τ )dt = ∑

2 × ei×n×ω0 ×t .

(2.70)

n=-¥

C-n

и, следовательно,

А так как

+¥

∑

2 × ei×n×ω0 ×τ

∑

2 × e-i×n×ω0 ×t ,

(2.71)

n=-¥

то автокорреляционная функция Rs (τ ) - четная и поэтому

Rs (τ ) = C02

+¥

+ 2∑

2 × e-i×n×ω0 ×t .

(2.72)

n=1

Четность автокорреляционной функции позволяет ее разложить в тригонометрический

ряд Фурье по косинусам

Rs (τ ) = a0

+¥

+ ∑ an × cos n ×ω 0 ×τ =

+ 2∑

2 × cos n ×ω0 ×τ .

(2.73)

n=1

В частном случае, при τ = 0 , получим:

+¥

Rs (0) = C02 + 2∑

n=1

Таким образом, автокорреляционная функция при τ = 0 представляет собой полную среднюю мощность периодического сигнала s(t ), равную сумме средних мощностей всех гармоник.

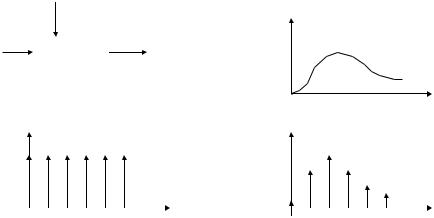
§2.10. Частотное представление импульсных сигналов

В предыдущем рассмотрении предполагалось, что сигналы непрерывны, однако при автоматической обработке информации часто используются и импульсные сигналы, а также преобразование непрерывных сигналов в импульсные. Это требует рассмотрения вопросов частотного представленияимпульсных сигналов.

Рассмотрим модель преобразования непрерывного сигнала в импульсную форму,

представленную на рис.2.6а.

a)		u(τ,t)	в) u(τ,t)
	x(t)		y(t)
	x(t)		y(t)

	T	τ
б) x(t)	г) y(t)
	t		t

Рис.2.6

Пусть на вход	импульсного модулятора поступает непрерывный сигнал x(t )
(рис.2.6б). Импульсный	модулятор формирует последовательность	единичных импульсов
(рис.2.6в) с периодом Т и длительностью импульсов τ, причем τ < T . Математическую
модель такой последовательности импульсов можно описать в виде функции u(τ , t ):
	1, если kT £ t £ kT + τ ;
	u(τ , t ) = 0, если kT + τ < t < (k +1)×T ,	(2.74)

где k - номер импульса в последовательности.

Выходнойсигналимпульсногомодулятора y(t ) (рис.2.6г) можнопредставитьввиде: y(t ) = u(τ , t )× x(t ).

На практике желательно иметь частотное представление последовательности импульсов. Для этого функцию u(τ , t ), как периодическую, можно представить в виде

ряда Фурье:

+¥

u(τ , t ) = ∑

n × e j×n×ωu

×t ,

(2.75)

n=-¥

где

∫

T u(τ , t )× e

- j×n×ωu

×t dt - спектральныекоэффициентыразложенияврядФурье;

(2.76)

ωu

2π

- частотаследованияимпульсов;

n - номергармоники.

Подставляя в выражение (2.76) соотношение (2.74), найдем Cn :

n =

u(τ , t )× e- j×n×ωu ×t dt =

e- j×n×ωu ×t dt = -

e- j×n×ωu ×t

1 - e- j×n×ωu ×τ

∫

× n ×ω

×T

j × n ×ω

×T

при n = 1,2,... ;

T u(τ , t )dt =

τ 1× dt = τ .

∫

Подставляя (2.76) в (2.74), получим:

+¥

1 - e

- j×n×ωu ×τ

+¥

j×n×ωu ×t

- e

- j×n×ωu ×(t -τ )

u(τ , t) = ∑

× e j×n×ωu ×t = ∑

j × n ×ωu × T

n=-¥ j × n ×ωu × T

n=-¥

= τ

+¥

j×n×ωu ×t

- e

- j×n×ωu ×t

- e

j×n×ωu ×(t-τ )

+ e

- j×n×ωu ×(t-τ )

+ ∑

j × n ×ωu × T

n=1

+¥

2[sin n ×ωu × t - sin n ×ωu (1 -τ )]

+ ∑

n ×ωu × T

n=1

Преобразуем разность синусов, тогда

(2.77)

(2.78)

			×	τ		× t - n ×ωu ×	τ
u(τ , t ) = τ	+¥	4 sin n ×ωu	×		× cos n ×ωu	× t - n ×ωu ×
	+ ∑			2			2	.	(2.79)
	+ ∑				n ×ωu ×T			.	(2.79)
T	n=1				n ×ωu ×T

Введем обозначение фазыn-ой гармоники

ωu	× τ = F .	(2.80)
	2

Тогда

				50
					τ
u(τ , t ) = τ		2τ	+∞	sin n ×π ×
	+	2τ	∑		T	× cos n × (ωu × t - F).	(2.81)
	+		∑	n ×π × τ		× cos n × (ωu × t - F).	(2.81)
T		T n=1		n ×π × τ

Таким образом, последовательность единичных постоянной составляющей бесконечное число гармоник Амплитуда k-ой гармоники определяется из выражения:

				τ
	2τ		sin k ×π ×
A =		×		T	.
			τ
k	T

k ×π ×

импульсов содержит наряду с с уменьшающейся амплитудой.

(2.82)

При цифровой обработке сигналов проводится дискретизация (квантование) по времени, то есть преобразование непрерывного сигнала в последовательность коротких импульсов. Как показано выше, любая последовательность импульсов имеет довольно сложный спектр, поэтому возникает естественный вопрос, каким образом процесс дискретизации по времени влияет на частотный спектр исходного непрерывного сигнала.

Для исследования этого вопроса рассмотрим математическую модель процесса дискретизации по времени, представленную на рис.2.7а.

Импульсный модулятор (ИМ) представляется в виде модулятора с несущей в виде идеальной последовательности очень коротких импульсов (последовательности δ-функций)

δ T (t ) , период следования которых равен Т (рис.2.7б).

На вход импульсного модулятора поступает непрерывный сигнал x(t )(рис.2.7в),

а на выходе образуется импульсный сигнал x (t ) (рис.2.7г).

a)		δT(t)	в) x(t)
	x(t)		x (t)
	x(t)	И.М.	x (t)
		И.М.

б) δT(t)

г) x (t)

0 T 2T 3T 4T 5T

T 2T 3T 4T 5T

Рис.2.7

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.05.20159.61 Mб38sbor.pdf
#
02.05.201575.45 Кб49SBORNIK_ZADACh_PO_ELEKTROMAGNETIZMU.docx
#
10.03.2016388.8 Кб67shedevr.docx
#
02.05.201589.41 Кб120Shpory_Baeva2.docx
#
20.09.2019403.99 Кб45Shpory_otredaktirovannye.docx
#
10.03.2016761.84 Кб14Signaly_1.pdf
#
02.05.2015181.28 Кб80Sputniki.docx
#
02.05.201552.2 Кб20Statistika.docx
#
02.05.201512.37 Mб1054Sveshnikova_I_S__Zapryagaeva_L_A__Guzeeva_I_V.pdf
#
02.05.20152.36 Mб54Teoria_odinochnogo_kadrovogo_snimka.docx
#
02.05.20151.54 Mб42Tmogi_Rusyaeva.docx