
Signaly_1
.pdf91
Для этого в программе задания последовательности импульсов заменить постоянный период следования импульсов, равный Ти , на переменный, функционально зависимый от x(t), т.е. Ти =Ти (x(t)). Можно взять зависимость Ти =Ти ×(1-0.5×x(t)), более грамотно-Ти =Ти ×(1-0.5×x(n×Tи)).
г). Построить графики исходного сообщения x(t) и модулированной по ширине последовательности импульсов Yш(t).
В этом случае в программе задания последовательности импульсов заменить постоянную длительность импульсов, равный t , на переменную, функционально зависимую от x(t), т.е. t = t (x(t)). Может быть взята зависимость Dt = t ×(1+2×x(t)), более грамотно- t = t ×(1+2×x(n×Tи)).
3.Промоделировать процессы аналого-цифрового преобразования. В качестве исходного сообщения взять гармонический сигнал x(t)=A×cos(k×t) длительностью Т равной 4 периода. Квантование по уровню произвести с постоянным шагом с использованием шести равных интервалов дискретизации, в качестве квантованных значений взять середины интервалов дискретизации. Квантование по времени произвести в соответствиии с теоремой Котельникова.
а). Построить графики исходного сообщения x(t) и соответствующего ему квантованного по уровню сообщения – Xк.у(t), которое, например при А=1, может быть задано следующим образом:
Xк.у(t):=if(x(t)<-2×A/3,-0.82, if(x(t)<-×A/3,-0.50, if(x(t)<0,-0.16, if(x(t)< A/3,0.16, if(x(t)<
2×A/3, 0.50, 0.82))))).
б). Построить графики исходного сообщения x(t) и соответствующего ему квантованного по времени сообщения – Xк.в(t).
В соответствии с теоремой Котельникова интервал между отдельными отсчетами ( t) находится из соотношения:
t=1/2×fm,
где fm=w/2×p (сек.-1)-максимальная циклическая частота в спектре сигнала; w- соответствующая ей круговая частота.
Следовательно в рассматриваемом случае fm=k/2×p, а t=p/k.
Поэтому для построения графика квантованного по времени сообщения Xк.в(t) достаточно построить в соответствующем формате отдельные значения исходного сообщения с интервалом t, т.е.
t1:=0, t .. 8×p/k
Xk.в.(t1):=A×cos(k×t1)
в) Провести квантование по времени квантованного по уровню сигнала Xk.у.(t).Построить график полученного сигнала.
Лабораторная работа №2
Преобразование сигналов из временной в частотную область.
Описание лабораторной работы выполнено с использованием программного продукта Mathcad.

92
Цель работы: Изучение методов получения Фурье-спектров (с помощью стандартных встроенных функций и аналитическим методом) и методов частотной фильтрации.
1.Использование стандартных встроенных функций.
Вэтом случае преобразование осуществляется над сигналами в виде массива
отсчетов |
сигнала (V ), число которых |
(i) равно 2m (m-целое |
число). Прямое |
||
|
i |
|
|
|
|
преобразование Фурье для вектора V выполняется с помощью стандартной встроенной |
|||||
функции |
fft(V ) . Результат |
преобразования представляется |
в виде |
вектора ( Al ) с |
|
количеством комплексных |
элементов |
равным 2m+1 + 1 . |
Данное |
преобразование |
|
переводит вектор Vi из временной или пространственной области в частотную.
Обратное преобразование осуществляется с помощью стандартной встроенной функции ifft(A), которая в качестве аргумента использует вектор А с комплексными элементами , число которых l = 2m−1 + 1, а результат представляется в виде вектора с числом элементов 2m .
Задание по п.1. Рассчитать частотный спектр прямоугольного импульса единичной амплитуды, представленного 32 равноотстоящими отсчетами (Т=32) с длительностью импульса равной t = 10 + k , где k - номер по списку. Представить частотный спектр как в комплексной форме, так и в виде амплитудно-частотной характеристики (АЧХ) и
фаза-частотной характеристики (ФЧХ).
С помощью обратного преобразования Фурье восстановить сигнал V1 по его |
||
|
|
i |
частотному спектру и сравнить с исходным сигналом Vi . |
|
|
Выполнение п.1: |
|
|
1. Задать исходный сигнал Vi : i:=0..31 |
Vi:=if( i < 10+k,1,0) |
|
2. Построить график сигнала Vi. |
|
|
3. Провести прямое преобразование Фурье сигнала Vi: |
А:=fft(V) |
|
4. Вычислить АЧХ (Мj) и ФЧХ (Qj) сигнала (Vi): |
|
|
j:=0…16
Mj:= 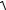
 [Re(Aj )]2 + [Im(Aj )]2
[Re(Aj )]2 + [Im(Aj )]2
Qj:= if (M j F 0, arg(Aj ),0) 5. Построить графики АЧХ и ФЧХ.
6. Восстановить сигнал по его частотному спектру V:=ifft(A), нарисовать его график и сравнить его с исходным сигналом.
2.Аналитический метод преобразования сигналов в частотную область.
Вэтом случае частотный спектр сигнала получают путем разложения его в ряд Фурье по следующим формулам:
|
S(t ) = |
a0 |
|
+ ∑(an × cos Wn t + bn × sin Wn t ), |
||
|
|
|||||
|
2 |
|
2π |
n |
||
где |
Wn = n × |
= n × W1 ; |
||||
|
||||||
|
|
|
|
T |
||
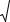
|
|
|
|
|
|
|
|
|
|
|
|
|
93 |
|
|
|
|
a0 |
|
T |
|
|
|
|
|
|
|
||||
|
|
|
= ∫ S(t )dt; |
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
an |
|
= |
|
2 |
|
T |
S(t )× cos Wn × tdt ; |
|
|
||||
|
|
|
T |
∫ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
b |
|
= |
2 |
∫ |
S (t)× sin W |
|
× tdt ; |
|
|
||||
|
|
|
T |
|
|
|
|||||||||
|
|
n |
|
|
|
|
|
n |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
или |
S(t ) = |
a0 |
+ ∑ An × cos(Wn × t + ϕ n ) |
|
|
||||||||||
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
n |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
An = |
an2 + bn2 ; |
ϕn = arctg |
n |
; |
||||||||||
an
An ,ϕ n - амплитуда и фаза n-ой гармоники соответственно.
Задание по п.2. Разложить в ряд Фурье (20 гармоник) периодический сигнал с периодом Т=1 сек. И длительностью единичного импульса Dt =(0,2+0,01 × k ) сек.,где k - номер по списку. Построить АЧХ (An (n)) и ФЧХ (Qn (n)). Синтезировать исходный
сигнал по формулам (1) и (2)с использованием с использованием различного числа гармоник (n=3,9,20).
|
Выполнение п.2. |
|
1. |
Задать исходный сигнал и построить его график: |
|
|
Т=1 |
t=0,0.001…T |
|
S(t ):= if (t < (0.2 + 0.01 × k ),1,0). |
|
2. |
Найти коэффициенты разложения а0, аn и bn по формуле (1) для 20 гармоник. |
|
3. |
Найти модуль амплитуды ( An ) и фазы ( Qn ) двадцати первых гармоник (n=1…20) и |
|
|
построить АЧХ и ФЧХ. |
|
4.Синтезировать сигнал по формулам (1) и (2) для различного числа гармоник (n=3,9,20), построить соответствующие графики и сравнить их с графиком исходного сигнала.
3.Частотная фильтрация сигналов с целью уменьшения влияния шумов.
Частотная фильтрация шумов основана на том, что шумы, как правило, имеют более высокочастотный спектр, чем полезный сигнал и, кроме того, их мощность, а следовательно и амплитуды их гармоник, значительно меньше по сравнению с амплитудами гармоник полезного сигнала. Исходя из этого частотную фильтрацию можно проводить путем нахождения спектра зашумленного сигнала и исключения из него гармоник с малой амплитудой (частотная фильтрация по уровню) или исключением из него высоко частотных гармоник (высокочастотная фильтрация). В дальнейшем по преобразованному таким образом спектру можно восстановить исходный полезный сигнал.
Задание по п.3. Произвести частотную фильтрацию по уровню и высокочастотную фильтрацию исходного сигнала, заданного своими 128-ю отсчетами вида:
|
|
i |
|
|
|
|
i |
|
|
|
|
qi |
= sin |
|
|
× (10 |
+ k )×π |
+ cos |
|
|
× (15 |
+ k )×π |
, |
|
|
||||||||||
|
128 |
|
|
|
128 |
|
|
|
|
||
зашумленного случайным шумом с максимальной амплитудой равной 1.

94
Фильтрацию провести при различных уровнях амплитуд исключаемых гармоник (не менее 3) и различных границах исключаемых высокочастотных гармоник (не менее 3). Полученные результаты сравнить с исходным полезным сигналом.
Выполнение п.3.
1. |
Задать полезный сигнал (qi ) , аддитивный шум (ri ) и зашумленный сигнал |
||
( Si = qi + ri ), i:=0,1..127 и построить их графики. |
|||
2. |
Найти комплексный частотный спектр с помощью стандартной встроенной |
||
функции |
F:=fft(S), j=0,1..64. |
||
|
|
|
|
3. |
Построить график АЧХ сигнала (модулей амплитуд гармоник) |
Fj |
. |
4. |
Произвести частотную фильтрацию по уровню исключая из спектра сигнала |
||
гармоники с амплитудами менее заданного уровня р (р=0.3,0.5,0.9). gi = if (Fj - p ³ 0, Fj ,0)
ивосстановить сигнал по преобразованному спектру S1:=ifft(g).
5.Построить графики восстановленных сигналов и сравнить их с исходным сигналом.
6.Произвести высокочастотную фильтрацию при различных границах исключаемых высокочастотных гармоник n (n=15,30,50).
g j := if (( j - n) £ 0, Fj ,0)
ивосстановить сигнал по преобразованному спектру: S 2 := ifft(g ).
7.Построить графики восстановленных сигналов и сравнить их с исходным сигналом.
95
Литература
1.Журкин И.Г., Шавенько Н.К. Автоматизация обработки аэрокосмической информации. М., МИИГАиК, 1989, с. 147.
2.Прэтт У. Цифровая обработка изображений. Кн.1,кн.2. М., Мир, 1982, с. 790.
3.Савиных В. П., Соломатин В.А. Оптико-электронные системы дистанционного зондирования. М., Недра, 1995, с.315.
4.Гоноровский И.С. Радиотехнические цепи и сигналы. Кн.1, кн.2. М., Советское радио, 1987, с. 438, 327.
5.Денисенко А.Н.,Стеценко О.А. Теоретическая радиотехника: справочное пособие Ч.1.: Детерминированные сигналы (методы анализа).-М.: Изд. Стандартов,1993.-
с. 215.
96
|
|
Оглавление |
|
Глава 1. Сигналы. |
4 |
||
1.1 |
Основные понятия и классификация. |
4 |
|
1.2 |
Модуляция сигналов. |
8 |
|
1.3 |
Непрерывные и импульсные модуляции. |
10 |
|
1.4 |
Цифровая модуляция. |
13 |
|
1.5 |
Дискретизация по уровню (квантование по уровню). |
14 |
|
1.6 |
Дискретизация (квантование) по времени или по текущей координате. |
18 |
|
1.7 |
Шумы. Общие понятия. |
22 |
|
Глава 2. Аналитическое моделирование сигналов. |
23 |
||
2.1 |
Общие подходы к моделированию сигналов. |
23 |
|
2.2 |
Математические модели представления детерминированых |
|
|
|
одномерных сигналов. |
24 |
|
2.3 |
Частотная форма представления детерминированых сигналов |
27 |
|
2.4 |
Математическое описание одномерных сигналов. |
29 |
|
2.5 |
Распределение энергии в спектре периодического сигнала. |
36 |
|
2.6 |
Преобразование Фурье. |
37 |
|
2.7 |
Основные свойства преобразования Фурье. |
41 |
|
2.8 |
Распределение энергии в спектре непериодического сигнала. |
44 |
|
2.9 |
Корреляционные функции детерминированых сигналов. |
46 |
|
2.10 |
Частотное представление импульсных сигналов. |
48 |
|
2.11 |
Влияние импульсного модулятора на спектр входного сигнала. |
52 |
|
2.12 |
Случайные сигналы. |
55 |
|
2.13 |
Стационарные случайные функции. |
60 |
|
2.14 |
Определение характеристик случайных функций по |
|
|
|
|
экспериментальным данным. |
62 |
2.15 |
Эргодическое свойство стационарных случайных функций. |
64 |
|
2.16 |
Спектральное представление случайных сигналов. |
65 |
|
2.17 |
Частотное представление стационарных случайных сигналов. |
68 |
|
2.18 |
Случайные поля при исследовании природных образований. |
72 |
|
|
97 |
|
2.19 |
Математическое описание непрерывных двумерных сигналов на |
|
|
примере изображений. |
74 |
2.20 |
Дискретное преобразование Фурье. |
85 |
Лабораторные работы. |
90 |
|
Литература. |
95 |
|
Оглавление. |
96 |
|
