
Signaly_1
.pdf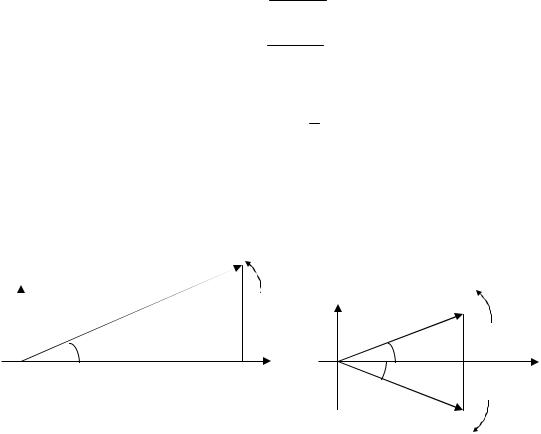
31
Еще одну форму комплексного представления гармонического сигнала можно получить исходя из формул Эйлера:
eix = cos x + i sin x, e−ix = cos x − i sin x,
cos x = eix + e−ix , 2
sin x = eix − e−ix . 2
В этом случае получаем следующее соотношение
S(t ) = A0 cos(ω0t + ϕ ) = 1 A0ei(ω0t+ϕ )
2
+ |
1 |
A e−i (ω0t+ϕ ) . |
(2.16) |
|
|||
2 |
0 |
|
|
|
|
||
Первой из этих форм соответствует векторное представление, изображенное на рис.2.3а.
ω0 |
|
|
|
|
|
Im |
|
|
|
ω0 |
|
A0 |
Im |
A0 |
|||
|
|||||
|
|
|
|||
|
|
2 |
|
|
|
ω0t+φ |
|
ω0t+φ |
|
||
B Re |
|
-(ω0t+φ) B |
Re |
||
а) |
|
б) |
-ω0 |
||
|
|
||||
Рис. 2.3
Действительная функция S(t ) получается в первом случае как проекция OB
вектора A0 на горизонтальную ось, а во втором – как сумма проекций OB на ту же ось двух векторов с амплитудами A0 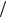 2 , вращающимися с угловой частотой ω0 во взаимнопротивоположных направлениях.
2 , вращающимися с угловой частотой ω0 во взаимнопротивоположных направлениях.
В соответствии с этим второе слагаемое в правой части выражения (2.16) можно трактировать как колебание с «отрицательной» частотой, что приводит к следующей записи:
32
S (t ) = |
1 |
A [ei(ω0t +ϕ ) + ei(−ω0t −ϕ ) ]. |
(2.17) |
|
|||
2 |
0 |
|
|
|
|
||
Нетрудно видеть, что в данном случае «отрицательные» частоты имеют формальный характер и связаны с применением комплексной формы для представления действительной функции времени. Хотя, если рассматривать частоту как скорость изменения фазы гармонического сигнала (ω (t) = ϕ ′(t)), то отрицательные частоты приобретают физический смысл и они равноправны с положительным.
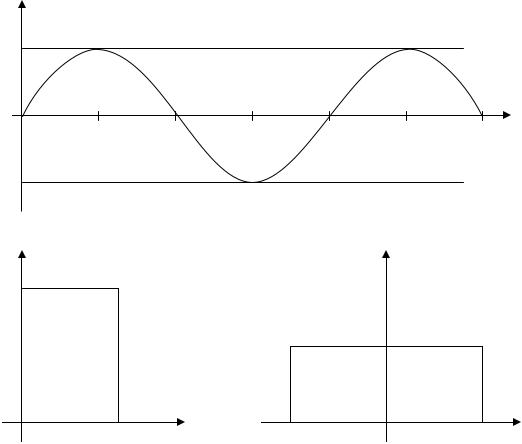
Графически амплитудный спектр гармонического сигнала S(t ) (рис.2.4а), может быть представлен как в виде, показанном на рис.2.4б, так и в виде, показанном на рис.2.4в.
S(t)
A0
T0/2 |
t |
T0 |
-A0
а)
A A
ω 0 |
= |
2π |
ω |
− ω 0 |
= − |
2π |
ω 0 |
= |
2π ω |
|
T0 |
|
|
|
|
||||||
|
T |
T |
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
0 |
|
б) |
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
Рис. 2.4 |
|
|
|
|
|
|

33
Пусть S(t ) - периодическая функция, заданная на интервале [t1 ;t2 ] и
удовлетворяющая условию Дирихле (то есть S(t ) – непрерывна на этом интервале или имеет конечное число точек разрыва первого рода). Таким образом,
S(t ) = S (t + T ) ,
где T = t |
- t = |
2π |
- период функции S(t ). |
|
|||
2 |
1 |
ω0 |
|
|
|
||
В этом случае сигнал S(t ) может быть представлен в виде ряда Фурье, то есть
может рассматриваться как сумма гармонических колебаний с угловыми частотами ω n
(представлен в тригонометрической форме):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω n = n × |
2π |
= n ×ω |
0 , |
|
n = 0,1,2,... , |
(2.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω0 = |
2π |
; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
причем |
|
ω0 |
|
|
|
|
|
|
называется основной частотой, а |
ω1 ,ω 2 ,Kω n - соответствующими |
||||||||||||||||||||
гармониками или обертонами. |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
Разложение производится по следующей формуле (тригонометрическая форма): |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
∞ |
|
|
|
|
|
|
a0 |
∞ |
|
|
|
|
|
|
|
S(t ) = |
|
+ ∑(an × cos nω0t + bn × sin nω0t) = |
+ ∑ An × cos(nω0t + ϕn ), |
(2.19) |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
n=1 |
|
|
|
|
|
|
2 |
n=1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где A |
= |
|
|
|
a 2 + b 2 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
n |
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
ϕn |
= -arctg |
bn |
; |
|
|
|
|
|
|
|
|
(2.20) |
|||||||||||||||||
an |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
a0 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
|
|
∫ S(t )dt |
- постоянная составляющая; |
|
|
|
(2.21) |
||||||||||||||||||||
2 |
|
T |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
− |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
T |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
an |
= |
2 |
|
|
2 |
|
S (t)cos nω0tdt ; |
|
|
|
(2.22) |
||||||||||||||||||
|
|
|
|
|
− |
T |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
b |
|
= |
2 |
|
2 |
S(t )sin nω tdt . |
|
|
|
(2.23) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
∫ |
|
|
|
|||||||||||||||||||
|
|
n |
|
|
|
T |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
−T
2
Ряд Фурье может быть записан и в комплексной форме:

34
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
||
|
|
|
|
|
|
¥ |
|
|
|
¥ |
|
|
|
|
|
|
|
¥ |
2 |
|
|
|
||||||
|
|
|
|
S(t ) = |
1 |
∑Cn × e |
+i (nω0t+ϕn ) = |
1 |
∑ |
Cn × einω0t = |
2 |
∑einω0t ∫ S(t)× e-inω0t dt , |
(2.24) |
|||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2 n=-¥ |
|
|
|
2 n=-¥ |
|
|
|
|
|
|
|
T n=-¥ |
- |
T |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(i × n ×ω0 ) = |
|
|
= |
2 |
2 |
|
S (t)× e-in×ω0t dt , |
|
|
|
|
|
(2.25) |
||||||
|
|
|
|
|
|
|
C |
Cn |
|
∫T |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
где |
|
|
n = Cn × e-iϕn |
= (an - ibn ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.26) |
|||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
-n = Cn × eiϕn = (an + ibn ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Следует еще раз подчеркнуть, что полученные тригонометрический и экспоненциальные разложения в ряд Фурье не являются двумя различными типами рядов, а выражают одно разложение двумя различными способами. Как видно из выше приведенных выражений, коэффициенты одного разложения можно выразить через коэффициенты другого:
|
|
|
a0 = C0 ; |
|
an = |
|
|
|
|
|
|
|
|
bn = i( |
|
n - |
|
-n ); |
|
|||||||||||||||
|
Cn + C-n ; |
|
C |
C |
(2.27) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
1 |
(a |
|
- ib ), |
|
|
|
= |
1 |
(a |
|
+ ib ). |
|
|
|||||||||||||
|
|
|
|
C |
n |
n |
C |
-n |
n |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
n |
|
|
|
|
2 |
|
|
n |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Амплитуды Сn и С-n являются взаимосопряженными комплексными |
||||||||||||||||||||||||||||||||||
величинами и отвечают условию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
× |
|
|
|
= (a |
|
- ib |
|
|
)(a |
|
|
+ ib |
|
) = a 2 |
+ b2 |
= A2 . |
(2.28) |
|||||||||||
|
|
C |
n |
C |
-n |
n |
n |
n |
n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
n |
|
||||||||||
При тригонометрическом виде представления функцию An |
= A(n ×ω 0 ) называют |
|||||||||||||||||||||||||||||||||
односторонним (не имеющим отрицательных частот) спектром амплитуд, а функцию
ϕ n |
= ϕ (n ×ω0 ) - называют спектром фаз (односторонним). |
|
|
||||||||
|
|
|
В случае |
экспоненциального |
вида представления |
ряда Фурье |
функцию |
||||
|
|
|
= C(i × n ×ω0 ) |
|
|
|
|
|
сигнала, |
||
Сn |
принято называть комплексным |
спектром |
периодического |
||||||||
если эту функцию (2.14) представить в виде |
|
|
|
||||||||
|
|
|
|
|
|
|
= C(i × n ×ω0 ) = C(n ×ω0 )× e-iϕn ; |
n = 0,±1,±2,... , |
(2.29) |
||
|
|
|
|
Сn |
|||||||
то функции C(n1 ×ω 0 ) |
и ϕ n = ϕ (n ×ω 0 ) |
называют соответственно спектром амплитуд и |
|||||||||
спектром фаз. |
|
|
|
|
|
|
|
|
|||
|
|
|
Таким образом, если известны спектры амплитуд и спектры фаз сигнала S(t ), то |
||||||||
в соответствии с (2.19) и (2.24), он может быть однозначно восстановлен. |
|
||||||||||
35
Как легко заметить из приведенных соотношений, спектры периодических сигналов определены только в дискретных точках n ×ω0 , поэтому спектры периодических сигналов называют линейчатыми или дискретными. Такие спектры принято изображать графически в виде вертикальных линий на частотах ω = n ×ω0 ,
причем высота каждой линии пропорциональна амплитуде или фазе соответствующей гармоники, что дает наглядное представление о «ширине спектра» и относительной величине отдельных ее составляющих.
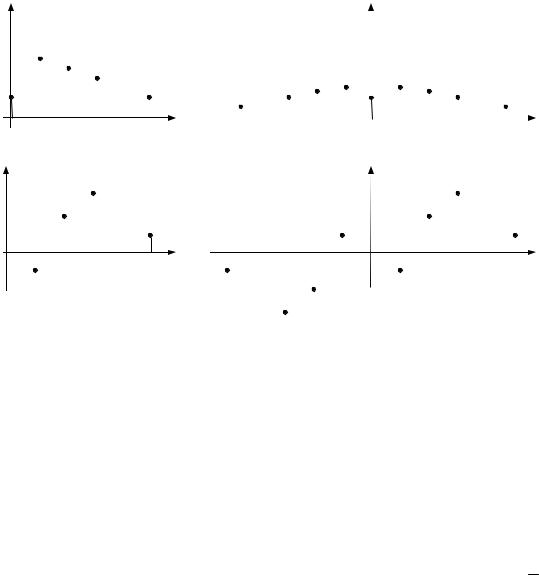
На рис.2.5а показаны примеры амплитуды и фазы одностороннего частотного спектра периодического сигнала, представленного в комплексной форме.
An |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
An |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
A1 |
|
|
A2 |
|
|
|
|
|
|
|
A |
|
A3 |
|
A |
A1 |
|
A1 |
|
A2 |
|
A |
|
A |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
A3 |
|
|
|
|
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
An |
|
|
|
n |
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
n |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
A0 |
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
A0 |
|
|
|
|
|
|
|
|
|
ω |
||||||||||||
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
||||||||||||||||||||
ω |
|
0 ω |
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
2 … |
ωn |
|
|
|
-ωn |
|
-ω2 -ω1 -ω0 |
ω0 |
ω1 |
ω2 |
ωn |
|
|||||||||||||||||||||||||||||||
φn |
|
|
|
|
φ3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φn |
|
|
φ3 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
φ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-φ1 |
|
|
|
φ2 |
|
|
|
|
|
|
φn |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ω0 |
|
|
|
|
|
|
… |
φn ω |
-ωn |
|
-ω2 -ω1 |
ω0 |
|
|
|
|
|
… |
|
|
ω |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
ω1 |
|
ω2 |
ωn |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
-ω0 |
|
|
|
ω1 |
ω2 |
|
|
ωn |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
φ1 |
|
|
|
|
|
|
|
|
|
-φn |
|
|
|
|
|
|
|
|
|
|
|
|
|
φ1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-φ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
-φ3 |
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Рис.2.5
Таким образом, две характеристики: амплитудная и фазовая каждой гармоники определяют частотный спектр периодического сигнала и однозначно его описывают.
Как видно из рис.2.5б двухсторонние спектры периодических сигналов обладают интересной особенностью: спектры амплитуд симметричны относительно оси ω = 0 , а спектры фаз симметричны относительно начала координат. Это легко доказать для общего случая. Действительно, исходя из выражений 2.14, 2.15, 2.16 Сn и
36
C−n являются комплексно-сопряженными величинами, следовательно Сn = С−n , то есть Сn - четная функция n и график функции Сn - симметричен относительно оси
ω = 0 .
Если Сn - действительная величина, то C−n - так же действительная величина и
Сn = С−n , а если Сn - комплексная величина, то
Сn = Cn × e−iϕn и C−n = Cn × eiϕn .
Следовательно ϕ n - нечетная функция n и ее график симметричен относительно
начала координат.
§2.5. Распределение энергии в спектре периодического сигнала
Положим, что сигнал S(t ) представляет собой периодическую функцию параметра t с периодом T. Средней за период мощностью сигнала назовем величину
|
T |
∫ |
|
|
W = |
1 |
T |
S 2 (t)dt , |
(2.30) |
|
|
|||
T |
|
|
|
|
|
|
0 |
|
|
аналогично тому, как определяется в физике мощность на активном сопротивлении величиной 1 Ом. Представим сигнал S(t ) в виде ряда Фурье в тригонометрической форме, тогда выражение (2.30) предстанет в виде:
|
|
1 |
T |
a |
0 |
∞ |
|
|
|
2 |
|
||
WT |
= |
|
∫ |
|
+ ∑(an |
× cos n ×ω0 × t + bn |
× sin n ×ω0 |
× t ) |
dt . |
(2.31) |
|||
T |
2 |
||||||||||||
|
|
0 |
|
n=1 |
|
|
|
|
|
||||
При возведении в квадрат правой части выражения (2.31) появятся слагаемые
следующих видов:
a |
0 |
|
2 |
|
|
|
|
|
|
|
|
1. |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
||
2. a 2 |
cos2 × n ×ω |
0 |
× t |
и |
b 2 |
×sin n ×ω |
0 |
×t ; |
|||
|
n |
|
|
|
|
|
n |
|
|
||
3. произведения синусов и косинусов с аргументами различной кратности.
|
|
|
a |
0 |
|
2 |
|
|
|
а2 |
||
Постоянная составляющая |
|
|
после интегрирования даст |
0 |
×Т . |
|||||||
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
Слагаемые второго вида после приведения к форме: |
|
|
||||||||||
|
an |
2 |
× (1 + cos 2 × n ×ω0 × t ) |
и |
b2 n |
(1- cos 2 × n ×ω0 ×t ) |
||||||
2 |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||

37
и интегрирования в пределах [0;T ] дают |
|
|
|
|||
|
a 2 |
|
b2 |
|||
|
n |
×T |
и |
n |
×T . |
|
2 |
2 |
|||||
|
|
|
||||
Последний вид слагаемых при интегрировании за период Т обращаются в нуль, как ортогональные функции.
Таким образом, средняя мощность сигнала за период Т выразится следующим
соотношением:
|
|
2 |
|
1 |
∞ |
|
|
|
|
|
|
|
1 |
∞ |
|
|
|
|
W |
= |
a0 |
+ |
∑ |
(a 2 |
+ b2 ) |
= |
S 2 |
+ |
∑ |
S 2 |
, |
(2.32) |
|||||
|
|
|
|
|||||||||||||||
T |
|
|
|
|
n |
n |
|
|
|
0 |
|
|
n |
|
|
|||
|
|
4 2 n=1 |
|
|
|
|
|
|
|
2 n=1 |
|
|
|
|
||||
где S0 = a0 - постоянная составляющая; 2
Sn - амплитуда n-й гармоники сигнала.
При использовании ряда Фурье в комплексной форме и с учетом (2.28) получим:
|
|
1 |
+∞ |
|
|
|
|
|
|
|
1 |
+∞ |
|
|
|
|
2 |
|
C 2 |
∞ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
WT |
= |
|
∑Cn |
× C−n |
|
= |
|
∑ |
|
Cn |
|
= |
0 |
+ ∑ |
|
Cn |
|
. |
(2.33) |
||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
4 n=−∞ |
|
|
|
|
|
4 n=−∞ |
|
|
|
|
2 |
n=1 |
|
|
|
|
|
||||||||
Итак, средняя мощность сигнала за период T равна сумме средних мощностей постоянной составляющей и гармоник. С энергетической точки зрения отдельные спектральные составляющие сложного периодического сигнала аддитивны, что является результатом ортогональности гармонических функций с кратными частотами.
Важно отметить, что мощность сигнала не зависит от величин фаз отдельных гармоник. Таким образом, изменение формы сигнала из-за изменений фазовых соотношений между отдельными гармониками, входящими в спектр сигнала, не влияет на среднюю мощность сигнала.
По виду функции Sn2 можно делать выводы о распределенной мощности в спектре периодического сигнала и, следовательно, определять полосу пропускания,
обеспечивающую достаточно полное использование мощности сигнала.
§2.6. Преобразование Фурье.
Любой физически реализуемый сигнал является ограниченным по частоте, по времени и обладает конечной энергией. Ограничение по частоте и энергии следует из инерционности и ограничения мощности реально реализуемых источников сигналов и если сигнал обладает конечной энергией, то он должен быть ограничен и во времени.

38
С математической точки зрения это означает, что функции S(t ), отображающие реальные сигналы, удовлетворяют условиям Дирихле и требованию абсолютной сходимости интеграла от модуля функции S(t ), то есть
+¥ |
|
∫ S (t )dt £ M , |
(2.34) |
-¥
где М - конечная величина.
Очевидно, что непериодический сигнал можно рассматривать как периодический с периодом (Т), стремящимся к бесконечности. Количество гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно
возрастать, так как при T → ∞ основная частота
ω 0 = |
2π |
|
(2.35) |
|
Т |
||||
|
|
|||
будет стремиться к нулю, а их амплитуды также будут стремиться к нулю. |
||||
Следовательно, расстояние между спектральными линиями, |
равное основной |
|||
частоте ω0 , становится бесконечно малым, а спектр - непрерывным (сплошным).
Таким образом, выражения для спектрального представления непериодического сигнала можно получить предельным переходом (при T → ∞ ) спектра периодического
сигнала, выраженного рядом Фурье.
Прямое и обратное преобразование Фурье для периодической функции SП (t)
запишем в форме, аналогичной (2.24):
+¥ |
|
|
|
|
|
|
|
|
|||||
SП (t) = |
1 |
∑ |
|
|
(i × n ×ω0 )× e+i×n×ω0 ×t ; |
||||||||
С |
|||||||||||||
|
|||||||||||||
|
|
|
2 n=-¥ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
T |
|
(2.36) |
||
|
|
|
|
|
|
2 |
2 |
|
|||||
|
|
(i × n ×ω0 ) = |
|
SП (t )e-i×n×ω0 ×t dt. |
|||||||||
С |
|
|
|
|
|
||||||||
|
T |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
∫T |
|||||
|
|
|
|
|
|
|
- |
|
|
|
|||
|
|
|
|
|
|
|
2 |
||||||
Периодический сигнал SП (t) преобразуется в непериодический сигнал S(t ) |
|||||||||||||
путем предельного перехода при T → ∞ . При этом основная частота ω0 уменьшается |
|||||||||||||
до dω , nω0 превращается в текущую частоту ω , а операция суммирования заменяется операцией интегрирования. Таким образом, ряд Фурье преобразуется в интеграл Фурье:
|
1 |
+¥ +¥ |
|
|
|
S(t ) = |
∫ ∫ S (t)× e-i×ω×t dt ei×ω×t dω . |
(2.37) |
|||
2π |
|||||
|
-¥ -¥ |
|
|
||
Внутренний интеграл, являющийся функцией ω ,
39
∞ |
|
S (iω ) = ∫ S (t)× e−iωt dt |
(2.38) |
−∞
называется прямым преобразованием Фурье, а результат этого преобразования S (iω )
называется комплексной спектральной плотностью или спектральной характеристикой функции S(t ). Внешний интеграл, являющейся функцией t,
|
1 |
∞ |
|
|||
S(t ) = |
∫ |
|
(iω )eiωt dω , |
(2.39) |
||
S |
||||||
2π |
||||||
|
−∞ |
|
||||
|
|
|
||||
называется обратным преобразованием Фурье. Эти соотношения безусловно справедливы только для абсолютно интегрируемой функции S(t ). Как видно из выражения (2.38), на каждой конкретной частоте значение соответствующей спектральной плотности, а следовательно, и амплитуды равно нулю. Из сравнения выражения (2.39) с рядом Фурье (2.24) видно, что бесконечно малому интервалу частоты dω соответствует составляющая с бесконечно малой комплексной амплитудой dCn = dC(i ×ω ), то есть
dC(iω ) = |
1 |
|
|
(i ×ω )dω . |
(2.40) |
|
S |
||||||
π |
||||||
|
|
|
|
|
Сравнение выражений (2.38) и (2.25) позволяет пояснить физический смысл понятия «спектральная плотность». Для этого выделив какую-либо дискретную частоту
ωn = n ×ω0 , соответствующую в случае периодической функции n-й гармонике, найдем амплитуду этой гармоники:
T
|
|
|
|
|
|
|
|
= |
|
(i ×ωn ) = |
2 |
2 S(t)× e−iωnt dt . |
(2.41) |
||||||
|
|
|
|
|
Сn |
C |
|||||||||||||
|
|
|
|
|
T |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Для непериодической функции, совпадающей с периодической на интервале |
||||||||||||||||
|
T |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = ωn , |
||
- |
|
; |
|
|
ее спектральная плотность, соответствующая той же частоте |
||||||||||||||
|
|
||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяется выражением : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(i ×ωn ) = ∫ S (t )× e−iωnt dt , |
(2.42) |
||||||||
|
|
|
|
|
|
|
|
S |
|||||||||||
−T
2
где T - конечно.
Так как интегралы в правых частях выражений (2.41) и (2.42) полностью совпадают, то

|
|
40 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(i ×ωn ) = |
|
T |
× |
|
(iωn ). |
|
(2.43) |
||||||
|
|
S |
C |
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|||||||||||
Учитывая, что |
|
|
|||||||||||||||||
|
|
|
|
|
|
T = |
1 |
, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
F0 |
|
|
||||||||
где F = |
ω0 |
- циклическая частота, соответствующая круговой частоте ω , получим: |
|||||||||||||||||
2π |
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
(iωn ) = |
|
|
(i ×ω n ) |
. |
|
|
|||||||||
|
|
|
|
|
C |
|
(2.44) |
||||||||||||
|
|
S |
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 × F0 |
|
|
||||||||
Множитель знаменателя 2 в правой части этого выражения учитывает то, что при использовании экспоненциальной формы ряда Фурье, в которой фигурируют отрицательные частоты, амплитуды гармоник равны половине амплитуд получаемых при одностороннем разложении.
Таким образом, значение спектральной плотности на частоте ω n равно отношению половины амплитуды гармоники ω n к основной частоте периодического сигнала, выраженной в герцах, которая равна полосе частот, отделяющей соседние линии дискретного спектра. Таким образом, физическая суть спектральной плотности – это плотность амплитуд и ее размерность [амплитуда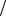 герц]. Из анализа соотношения
герц]. Из анализа соотношения
(2.44) вытекает важное положение: непрерывный спектр (модуль спектральной плотности) непериодической функции и огибающая линейчатого спектра периодической функции совпадают по форме и отличаются только масштабом:
Сn |
= |
2 × S (ω n ) |
= |
ω0 |
× S (ω n ). |
|
π |
||||
|
|
T |
|
||
Из выражения (2.38) с учетом формулы Эйлера можно получить выражение для спектральной плотности (S (iω )), а, следовательно, и прямое преобразование Фурье, в
тригонометрической форме:
|
|
+∞ |
+∞ |
|
|
|
(iω ) = ∫ S(t )× cosω tdt - i ∫ S(t)× sin ω tdt . |
(2.45) |
|
S |
||||
|
|
−∞ |
−∞ |
|
Спектральная плотность S (iω ) величина комплексная, поэтому для нее справедливо следующее представление
|
|
(iω ) = A(ω ) - i × B(ω ) = S (ω )× e−iψ (ω ) , |
(2.46) |
S |
+∞
где A(ω ) = ∫ S(t )× cosω tdt - действительная часть S (iω );
−∞
