
- •1. Информатика как наука
- •1.1. Общее представление об информации
- •1.2. Свойства информации
- •Контрольные вопросы
- •2. Организация компьютерной системы
- •2.1. Основные принципы построения компьютерной системы
- •2.2. Основные блоки фон-неймановской компьютерной системы
- •2.3. Архитектура компьютерной системы
- •2.4. Основные компоненты компьютерной системы
- •2.5. Программное обеспечение
- •Контрольные вопросы
- •Двоичная система кодирования
- •3.2. Системы счисления
- •Позиционные системы счисления
- •3.3. Правила двоичной арифметики. Операция сдвига по разрядной сетке
- •3.4. Перевод чисел из одной позиционной системы счисления в другую
- •Контрольные вопросы
- •Варианты практических заданий по теме «Системы счисления»
- •4. Формы представления данных в компьютере
- •4.1. Форма представления двоичных чисел с фиксированной запятой
- •Примеры записи двоичных чисел в прямом, обратном и дополнительном кодах
- •4.2. Форма представления двоичных чисел с плавающей запятой
- •Операция денормализации/нормализации (стандарт IEEE 754)
- •4.3. Представление символьной информации в компьютере
- •Контрольные вопросы
- •Варианты практических заданий по теме «Формы представления данных в компьютере»
- •5. Операционные системы
- •5.1. Назначение и функции операционной системы
- •5.2. Структуры операционных систем
- •5.3. Операционная среда Windows
- •Контрольные вопросы
- •6. Основы алгебры логики
- •6.1. Основные понятия алгебры логики
- •6.2. Двойственные аксиомы и теоремы алгебры логики
- •6.3. Способы представления логических функций
- •Контрольные вопросы
- •Варианты практических заданий по теме «Основы алгебры логики»
- •Библиографический список

Таким образом, есть возможность выражать конъюнкцию через дизъюнкцию и отрицание или дизъюнкцию – через конъюнкцию и отрицание. Законы де Моргана и следствия из них справедливы для любого количества переменных.
6.3. Способы представления логических функций
Табличный способ представления логической функции. |
В данном случае ЛФ представля- |
||||||
ется своей таблицей истинности. |
|
|
|
|
|
|
|
Например, представление ЛФ трех аргументов f(x1, x2, x3) ее таблицей истинности: |
|||||||
|
№ |
|
Набор |
|
|
Значение |
|
|
набора |
x1 |
x2 |
x3 |
|
функции |
|
|
0 |
0 |
0 |
0 |
|
1 |
|
|
1 |
0 |
0 |
1 |
|
0 |
|
|
2 |
0 |
1 |
0 |
|
0 |
|
|
3 |
0 |
1 |
1 |
|
1 |
|
|
4 |
1 |
0 |
0 |
|
1 |
|
|
5 |
1 |
0 |
1 |
|
0 |
|
|
6 |
1 |
1 |
0 |
|
1 |
|
|
7 |
1 |
1 |
1 |
|
0 |
|
Табличный способ является максимально наглядным, но в случае сложных функций алгебры логики (ФАЛ) он недостаточно компактен.
Аналитический (алгебраический) способ представления логической функции
Аналитический (алгебраический) способ представления логической функции – это аналитическая запись функции в виде формулы, по которой можно реализовать логическое устройство, состоящее из логических элементов, каждый из которых реализует элементарную логическую операцию. В результате операции, выполняемой логическим элементом, на его выходе появляется сигнал «да» – 1 или «нет» – 0, таким образом, это действие может быть выражено двоичным кодом.
Любая сложная логическая операция может быть разложена на элементарные логические функции – «НЕ» (логическое отрицание), «ИЛИ» (дизъюнкция), «И» (конъюнкция). Например,
f1(x1, x2 , x3) = x3 + x1 x2 + x2 x3 + x1 x2 x3
f2 (x1, x2 , x3 ) = (x1 + x2 ) (x2 + x3 ) (x1 + x2 + x3 )
Макстерм H (дизъюнктивный терм) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком дизъюнкции (например, для f2 (x1, x2 , x3 ) : x1 + x2 + x3 – макстерм
максимального ранга, так как присутствуют все переменные функции). Элементарная сумма – это дизъюнкция нескольких переменных или их отрицаний (например, дляf2(x1, x2, x3): x1 + x2 ).
Минтерм F (конъюнктивный терм) – это ЛФ, связывающая все переменные в прямой и инверсной форме (литералы) знаком конъюнкции (например, для f1(x1, x2, x3): x1 x2 x3 – минтерм
максимального ранга, так как присутствуют все переменные функции). Элементарное произведение – это конъюнкция нескольких переменных или их отрицаний (например, для f1(x1, x2, x3):
x2 x3 ).
Нормальные формы аналитического представления ЛФ:
•нормальная дизъюнктивная форма (НДФ) – это ∑Fi или Fi, где Fi – минтермы любого
ранга, включая единичный, ∑ и |
– знаки логического сложения; |
|
|
• |
нормальная конъюнктивная форма (НКФ) – это ПHi или Hi, где Hi – макстермы любого |
||
ранга, |
включая единичный, П и |
– знаки логического умножения; |
|
• |
совершенная нормальная дизъюнктивная форма (СНДФ) – это ∑Fi или |
Fi, где Fi – мин- |
|
термы только максимального ранга; |
|
||
• |
совершенная нормальная конъюнктивная форма (СНКФ) – это ПHi или |
Hi, где Hi – мак- |
|
стермы только максимального ранга. |
|
||
Любая совершенная нормальная форма (СНФ) отличается от нормальной тем, что всегда содержит термы только максималь-ного ранга и дает однозначное представление логической функции.
34

Любая таблично заданная ФАЛ (ЛФ) может быть пред-ставлена аналитически в виде дизъюнкции конечного числа минтермов, т.е. НДФ и СНДФ. На каждом из минтермов функция равна единице:
f(x1, x2,..., xn) = F0+ F1 + ... +Fn-1 = ∑ Fi =  Fi,
Fi,
11
i– номера наборов, на которых функция равна единице.
СНДФ функции находится следующим образом: формируется дизъюнкция произведений (минтермов) всех аргументов с количе-ством слагаемых, равным числу наборов, на которых функция равна единице; в каждом минтерме над аргументом, значение которого равно нулю, ставится знак отрицания. Например, записать в аналитической форме функцию, заданную таблично:
x1 |
x2 |
x3 |
f(x1, x2, x3) |
x1 |
x2 |
x3 |
f(x1, x2, x3) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
СНДФ функции:
f(x1, x2, x3)= F0(0, 0, 0)+ F3(0, 1, 1)+ F4(1, 0, 0)=
= x1 x2 x3 + x1 x2 x3 + x1 x2 x3
Для реализации логического устройства по СНКФ функции потребуется три логических элемента, производящих конъюнкцию (&), и один логический элемент, производящий дизъюнкцию (1) рис. 1.
х1 |
& |
|
|
|
|
|
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3 |
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
& |
|
|
|
1 |
f(х1, х2, х3) |
||
|
|
|
|||||
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х3
х1 &
х2  х3
х3 
Рис. 1
Для упрощения логического устройства можно получить НДФ функции, произведя соответствующие упрощения в ее СНДФ:
f (x1, x2 , x3 ) = x1 x2 x3 + x1 x2 x3 + x1 x2 x3 = = x2 x3 (x1 + x1) + x1 x2 x3 = x2 x3 + x1 x2 x3
Таким образом, для реализации логического устройства вместо трех логических элементов, производящих конъюнкцию, по-требуются только два, т.е. можно получить более оптимальное устройство (рис. 2).
x2  &
&
x3 
1 f(x1, x2, x3)
х1  &
&
х2 х3
35
Рис. 2
Любая таблично заданная ФАЛ может быть представлена аналитически в виде конъюнкции конечного числа макстермов, т.е. НКФ и СНКФ. На каждом из макстермов функция равна нулю:
f(x1, x2,..., xn) = H0 & H1 &… &Hn-1 = ПHi = 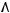 Hi. 0 0
Hi. 0 0
Используя правила двойственности, СНКФ функции находят следующим образом: формируют произведение дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых функция равна нулю; в каждом макстерме над аргументом, равным единице, ставят знак отрицания.
СНКФ функции для предыдущего примера:
f (x1, x2 , x3 ) = H1(0, 0,1) & H2 (0,1, 0) & H5 (1, 0,1) & H6 (1,1, 0) & H7 (1,1,1) = (x1 + x2 + x3 ) & (x1 + x2 + x3 ) & (x1 + x2 + x3 ) &
(x1 + x2 + x3 ) & (x1 + x2 + x3 )
Для реализации логического устройства по СНКФ функции потребуется пять логических элементов, производящих дизъюнкцию, и один логический элемент – конъюнкцию. Любую СНКФ функции можно привести к ее СНДФ и наоборот. Для упрощения логического устройства можно произвести соответствующие упрощения в полученной СНКФ функции и привести ее к НДФ:
f (x1, x2, x3) =
= (x1 + x1 x2 + x1 x3 + x1 x2 + 0 + x2 x3 + x1 x3 + x2 x3 + 0) & (x1 + x1 x2 + x1 x3 + x1 x2 + 0 + x2 x3 + x1 x3 + x2 x3 + 0) &
(x1 + x2 + x3) = (x1 (1 + x2 + x3 + x2 + x3) + x2 x3 + x2 x3) & (x1 (1 + x2 + x3 + x2 + x3) + x2 x3 + x2 x3) & (x1 + x2 + x3) =
= (x1 + x2 x3 + x2 x3) & (x1 + x2 x3 + x2 x3) & (x1 + x2 + x3) =
= (0 + x1 x2 x3 + x1 x2 x3 + x1 x2 x3 + x2 x3 + 0 + x1 x2 x3 +
0 + x2 x3) & (x1 + x2 + x3) = (x2 x3 (x1 + x1 +1) + x2 x3 (x1 +1)) &
(x1 + x2 + x3) = (x2 x3 + x2 x3) & (x1 + x2 + x3) = x1 x2 x3 +
0 + 0 + x1 x2 x3 + x2 x3 + x2 x3 = x1 x2 x3 + x1 x2 x3 + x2 x3 = = x1 x2 x3 + x2 x3 (x1 +1) = x1 x2 x3 + x2 x3
Каждая ФАЛ, в общем случае, может иметь несколько НДФ или НКФ, но только одну СНДФ и одну СНКФ. Нормальные формы можно получить из совершенных после возможных упрощений выражений.
П р и м е р. Записать в аналитической форме функцию, задан-ную таблицей истинности:
x1 |
x2 |
x3 |
f(x1, x2, x3) |
x1 |
x2 |
x3 |
f(x1, x2, x3) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
CНДФ функции:
f (x1, x2 , x3) = F0 (0, 0, 0) + F1(0, 0,1) + F3(0,1,1) + F4 (1, 0, 0) +
F6 (1,1, 0) = x1 x2 x3 + x1 x2 x3 + x1 x2 x3 + x1 x2 x3 + x1 x2 x3
Для реализации логического устройства по СНДФ потребуется пять логических элементов, осуществляющих конъюнкцию, и один логический элемент, осуществляющий дизъюнкцию. Чтобы упростить логическое устройство, можно, произведя соответствующие упрощения в СНДФ функции, перейти к ее НДФ:
36
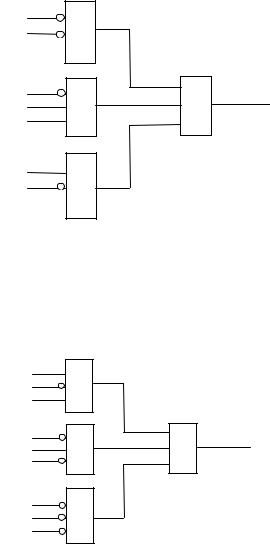
f (x1, x2 , x3 ) = x1 x2 (x3 + x3 ) + x1 x2 x3 + x1 x3 (x2 + x2 ) =
= x1 x2 + x1 x2 x3 + x1 x3
Теперь для реализации логического устройства вместо пяти логических элементов, производящих конъюнкцию, потребуются только три (рис. 3).
х1 |
& |
|
|
х2 |
|
|
|
3 |
|
|
|
х1 |
& |
1 |
f(х1, х2, х3) |
х2 |
|
|
|
х3 |
|
|
|
х1 |
& |
|
|
х3 |
|
|
|
3 |
|
|
|
Рис. 3
CНКФ функции:
f(x1, x2 , x3 ) = H2 (0,1, 0) & H5 (1, 0,1) & H7 (1,1,1) =
=(x1 + x2 + x3 ) & (x1 + x2 + x3 ) & (x1 + x2 + x3 )
Для реализации логического устройства по СНКФ функции потребуются три логических элемента, производящих дизъюнкцию, и один логический элемент – конъюнкцию (рис. 4).
х1 |
1 |
|
х2 |
|
|
х3 |
|
|
х1 |
1 |
& f(х1, х2, х3) |
х2 |
|
|
х3 |
|
|
х1 |
1 |
|
х2 |
|
|
х3 |
|
|
Рис. 4
Используя соответствующие преобразования, СНКФ функции можно привести к ее СНДФ.
Преобразование нормальных форм логической функции в совершенные нормальные формы
Преобразование НДФ логической функции в СНДФ. НДФ логической функции представлена минтермами не только максимального ранга, поэтому, чтобы преобразовать НДФ функции в СНДФ, т.е. получить все минтермы только максимального ранга, необходимо произвести конъюнкцию каждого минтерма НДФ с логической суммой (дизъюнкцией) недостающей в минтерме логической переменной и ее инверсии. Так как дизъюнкция логической переменной и ее инверсии равна логической единице, то такое действие не изменит результат минтерма. Если максимальный ранг для функции равен r (функция r переменных), а ранг i-го минтерма равен k, где k < r, то преобразование необходимо применить к i-му минтерму r − k раз.
П р и м е р. Преобразовать НДФ логической функции f (x1, x2 , x3 ) = x1 x2 + x1 x2 x3 + x1 x3 в СНДФ:
f(x1, x2, x3)= x1 x2 + x1 x2 x3 + x1 x3
37
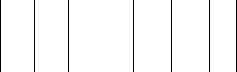
F1 F2 F3
Так как минтерм F2 имеет максимальный ранг, то преобразования необходимо применить только к минтермам F1 и F3:
F1 = x1 x2 (x3 + x3 ) = x1 x2 x3 + x1 x2 x3 F3 = x1 x3 (x2 +x2 ) = x1 x2 x3 + x1 x2 x3
СНДФ данной функции:
f (x1, x2 , x3 ) = x1 x2 x3 + x1 x2 x3 + x1 x2 x3 + x1 x2 x3 +
+ x1 x2 x3
Преобразование НКФ логической функции в СНКФ. НКФ логической функции представлена макстермами не только максимального ранга, поэтому, чтобы преобразовать НКФ функции в СНКФ, т.е. получить все макстермы только максимального ранга, необходимо произвести дизъюнкцию каждого макстерма НКФ с конъюнкцией недостающей в макстерме логической переменной с ее инверсией. Так как конъюнкция логической переменной с ее инверсией равна логическому нулю, то такое действие не изменит результат макстерма. Если максимальный ранг для функции равен r (функция r переменных), а ранг i-го макстерма равен k, где k < r, то преобразование необходимо
применить к i-му макстерму r − k раз. |
|
|
|
||
П р и м |
е р. |
Преобразовать |
НКФ |
логической |
функции |
f (x1, x2 , x3 ) = (x1 |
+ x2 ) & (x2 + x3 ) & (x1 + x2 + x3 ) в СНКФ: |
|
|
||
|
f (x1, x2 , x3 ) = (x1 + x2 ) & (x2 + x3 ) & (x1 + x2 +x3 ) |
|
|||
|
H1 |
H2 |
H3 |
|
|
Так как макстерм H3 имеет максимальный ранг, то преобразования необходимо применить только к макстермам H1 и H2:
H1 = (x1 + x2 ) +x3 x3 = (x1 + x2 + x3 ) & (x1 + x2 + x3 ) H2 = (x2 + x3 ) + x1 x1 = (x1 + x2 + x3 ) & (x1 + x2 + x3 )
СНДФ данной функции:
f (x1, x2 , x3 ) = (x1 + x2 + x3 ) & (x1 + x2 + x3 ) & (x1 + x2 + x3 ) &
(x1 + x2 + x3 ) & (x1 + x2 + x3 ) = (x1 + x2 + x3 ) & (x1 + x2 + x3 ) &
(x1 + x2 + x3 )
Представление логической функции таблицей истинности по совершенным нормальным формам
По СНДФ и СНКФ можно представить функцию таблицей истинности. Например, представить логическую функцию таблицей истинности по CНДФ:
f (x1, x2 , x3 ) = x1 x2 x3 + x1 x2 x3 + x1 x2 x3 ,
f (x1, x2 , x3 ) = F5 (1, 0,1) + F3 (0,1,1) + F4 (1, 0, 0)
Таблица истинности будет следующей:
x1 |
x2 |
x3 |
f(x1, x2, x3) |
x1 |
x2 |
x3 |
f(x1, x2, x3) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Например, представить логическую функцию таблицей истинности по СНКФ:
f (x1, x2 , x3 ) = (x1 + x2 + x3 ) & (x1 + x2 + x3 ) & (x1 + x2 + x3 ) f (x1, x2 , x3 ) = H2 (0,1, 0) & H4 (1, 0, 0) & H5 (1, 0,1)
x1 |
x2 |
x3 |
f(x1, x2, x3) |
x1 |
x2 |
x3 |
f(x1, x2, x3) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
38
