10.Нечеткие множества и основные операции над ними.

В 1965г. Заде предложил теорию нечетких или размытых множеств, получивших также название нечеткой логики. Нечеткая логика предполагает неточные, приблизительные, примерные оценки. Необходимость такого подхода вызвана тем, что:

- в некоторых ситуациях невозможно или не нужно точное определение параметров;

- по мере роста сложности систем постепенно падает наша способность делать точные и в то же время значащие утверждения относительно ее поведения, пока не будет достигнут порог, за которым точность и значимость становятся почти взаимоисключающими характеристиками.

Конечное нечёткое множество А из универсального множества U– это множество упорядоченных пар:

A={u_i,µ_A(u_i)}, u_i ϵ U

Где µ_A(u_i)– значение истинности, определяющее функцию принадлежности, которая указывает предполагаемую степень принадлежности этому множеству.

В нечётких множествах функция принадлежности (мера членства) задаётся на интервале [0,1] часто в виде точки этого интервала. Если µ_A(u_i)может принимать значения в интервале [0,1] иµ_A(u_i)=0 будет означать, что элементu_i не принадлежит множествуA,µ_A(u_i)=1 означает, чтоu_i принадлежит множествуA, а любое значение0<µ_A(u_i)<1 определяет степень принадлежностиu_i множеству А, тогда А – нечёткое множество. При этомµ_A(u_i)может быть как непрерывной, так и дискретной.

Пример. Пусть Х – множество отечественных машин.

Х={“Волга”,”Запорожец”,”Москвич”,”Жигули”}. Тогда можно определить нечёткое множество А хорошихмашин так: А={(“Волга”;1), (“Запорожец”;0.4), (“Москвич”;0.6), (“Жигули”,0.8)}. Функция принадлежности выбирается субъективно, зависит от субъекта, его настроения, цели построения множеств и т.д.

Такие операции над классическими множествами как объединение, пересечение, дополнение и т.п. могут быть определены и для нечетких множеств.

Объединением двух нечетких множеств A иB называется множествоC , обозначаемоеC AB A OR B, функция принадлежности которого задается выражением:

Можно сказать, что объединением двух нечетких множеств является множество - «наименьшее» среди всех, которые включают оба эти множества.

Пересечением двух нечетких множеств A и B называется множество C , обозначаемое C AB A AND B , функция принадлежности которого задается выражением:

Как и в предыдущем случае, определение можно интерпретировать, так: пересечением двух множеств является «наибольшее» среди всех, которые включены и в A, и в B

Дополнением (отрицанием) нечеткого множества A называется множество, обозначаемое A или A , илиNOT A , функция принадлежности которого определяется выражением:

Рис. 6 иллюстрирует вышеперечисленные стандартные операции над множествами.

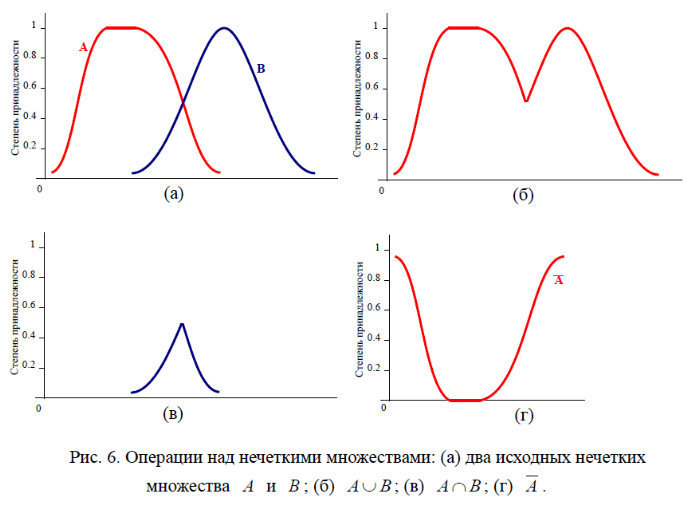
Можно рассматривать различные операции над нечеткими множествами по аналогии с четкими множествами. Наиболее распространенными являются определения отношений вложения, дополнительного нечеткого множества, произведения нечеткого множества и суммы нечетких множеств. Их обычно записывают в следующем виде: