
- •1. Теория принятия решений: задача принятия решений, цель, проблема, проблемная ситуация.
- •2.Измерения при формировании решений: ранжирование, парное сравнение, непосредственная оценка, виды неопределенностей и их измерение.
- •3.Виды экспертиз.
- •4.Метод Дельфы
- •5. Дерево целей и решений.
- •6.Определение усредненного мнения экспертов (среднее арифметическое, среднее геометрическое, мода, медиана Кемени
- •7.Определение согласованности мнений экспертов (коэффициент конкордации).
- •8.Виды критериев оптимальности и их содержание.
- •9. Критериальный анализ ситуации: метод базовых шкал, ранжирование и выбор критериев.
- •10.Нечеткие множества и основные операции над ними.
- •11.Экспертные методы определения функций принадлежности.
- •12. Аналитический и оптимизационный методы определения функций принадлежности.
- •13. Нечеткая задача оптимизации выбора вариантов проектов.
- •14. Модели стохастического математического программирования
- •15. Генерация альтернатив решений: понятие генетического алгоритма.
- •16. Генерация альтернатив решений: Дерево решений
- •17. Многокритериальная оптимизация. Проблемы многокритериальной оптимизации
- •18. Многокритериальная оптимизация. Множество Парето.
- •19. Многокритериальная оптимизация. Метод идеальной точки.
- •20. Принятие решений по многим критериям: Метод последовательных уступок
- •21. Принятие решений по многим критериям: Парето оптимальное решение
- •23.Принятие решений по многим критериям: Гарантированные достоинства и недостатки.
- •24.Принятие решений по многим критериям: Правило Борда.
- •25.Принятие решений по многим критериям: Принцип Беллмана-Заде
- •26. Принятие решений по многим критериям: Турнирная таблица
- •30.Согласование групповых решений: принцип большинства голосов, принцип диктатора, принцип вето, идеальной точки, консенсус.
- •31.Согласование групповых решений по Парето.
- •32. Согласование групповых решений: Метод идеальной точки
- •33. Марковская модель согласования решений.
- •34. Согласования групповых решений. (принципы Курно, Парето, Эджворта).
- •35. Теория игр: платежная матрица, чистые и смешанные стратегии, решение игры.
- •36. Решение игры в чистых стратегиях. Игры с седловой точкой.
- •37.Решение игры в смешанных стратегиях. Теорема фон Неймана.
- •38.Решение матричных игр МхN (сведение к задаче линейного программирования).
- •39.Игры с природой (теория статистических решений). Особенности платежной матрицы.
- •40.Байесовские стратегии в играх с природой (частичная неопределенность).
- •41. Критерии принятия решений в играх с природой (полная неопределенность).
- •42.Марковские процессы с дискретным временем: основные понятия и определения.
- •43.Игры с природой: оценка риска
40.Байесовские стратегии в играх с природой (частичная неопределенность).
При частичной неопределенности в качестве показателя эффективности (критерия), который необходимо обратить в максимум принимается среднее значение (математическое ожидание) выигрыша игрока А с учетом всех возможных вероятностей Q(Пj). В этом случае за несколько партий мы получим среднее значение выигрыша (математическое ожидание) – критерий Байеса –Лапласа (B-L – критерий) :
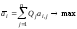 ,
,
где
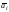 – взвешенное среднее.
– взвешенное среднее.
Оптимальной стратегией А* = Аi будет та, которая удовлетворяет этому условию.
В результате задача сводится к поиску решения в среднем.
Средний риск:

Можно показать,
что стратегия максимизации āi
и минимизации
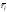 одна и та
же. В случае, когда известны вероятности
Q1,
Q2
…. Qn,
при решении игры с природой всегда можно
обойтись чистыми стратегиями, не применяя
смешанных стратегий, то есть:
одна и та
же. В случае, когда известны вероятности
Q1,
Q2
…. Qn,
при решении игры с природой всегда можно
обойтись чистыми стратегиями, не применяя
смешанных стратегий, то есть:
средний выигрыш
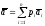 – это среднее взвешенное среднего
выигрыша, соответствующее чистым
стратегиям и:
– это среднее взвешенное среднего
выигрыша, соответствующее чистым
стратегиям и:

Поэтому принятие смешанной стратегии игроком А не может быть выгоднее с любыми вероятностями Пi, чем применение чистой стратегии А* = Аi.
Если в качестве
оптимальной стратегии выбирается та
из них, для которой величина
āi
обращается в максимум, соответственно
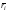 в минимум,
то такая
стратегия
называется байесовской..
Эта стратегия
является чистой
в минимум,
то такая
стратегия
называется байесовской..
Эта стратегия
является чистой
41. Критерии принятия решений в играх с природой (полная неопределенность).
1. Максиминный
критерий Вальда (критерий пессимизма
-всегда рассчитывай на худшее) - худший
результат объявляется минимальным
выигрышем, то есть: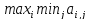
2. Критерий
Сэвиджа (любыми путями избежать
большого риска) - худшим объявляется не
минимальный выигрыш, а максимальная
потеря выигрыша по сравнению с тем, чего
можно было бы добиться в данных условиях: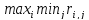
3. Критерий Гурвица (критерий пессимизма-оптимизма) - степень пессимизма оценивается экспертами критериема

где а = 1, ... ,n. Приа = 1 получаем критерий Вальда.
Одним из центральных вопросов теории игр с природой является вопрос о том, как могут помочь в принятии решений эксперименты, направленные на выяснение действительных состояний природы. Речь здесь идет, прежде всего, о выводах из экспериментов, об их планировании и обработке. Как правило, при планировании эксперимента рассматривается следующий вопрос.
Нам предстоит предпринять некоторую операцию в недостаточно выясненных условиях, например, бурить или не бурить скважину, выполнять гидроразрыв пласта или нет и т.д. Имеет смысл для уточнения условий в нашей неопределенной ситуации предпринять некоторый эксперимент ξ. Но на проведение эксперимента требуются средства. Если эксперимент дорог, он не проводится, если достаточно дёшев - ответ положительный. Расчеты о целесообразности проведения эксперимента производятся исходя из среднего риска.
Эксперименты бывают двух типов:
- идеальный эксперимент, после которого мы точно знаем состояния природыПj
- неидеальный эксперимент, который не приводит к точному вычислению состояний природыПj.
42.Марковские процессы с дискретным временем: основные понятия и определения.
Марковских случайных процессы с дискретным временем нашли применение для прогноза множества показателей, которые меняются щ года в год одновременно, но непосредственно связи между ними не установлены ввиду отсутствия информации или крайней сложности этих связей. Примером может служить прогноз потребностей народного хозяйства в ресурсах. При этом, однако, при реализации данного прогноза устанавливается на перспективу сама структура потребления ресурсов различными отраслями.
Марковский случайный процесс с дискретным временем задается графом состояний элементов системы и матрицей вероятностей Кодов элементов системы из состояния в состояние. Обычно при исследовании такого процесса интересуются вероятностями пребывания системы в j-м состоянии.
Для вычисления вероятности перехода в j-oeсостояниеPj- на к-м шаге существует соотношение Колмогорова - Чепмена:
 ,
,
Где
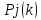 – вероятность пребывания элементов
системы вj-ом состоянии
наk-ом шаге (вk-й
дискретный интервал времени),
– вероятность пребывания элементов
системы вj-ом состоянии
наk-ом шаге (вk-й
дискретный интервал времени),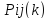 -
вероятности перехода системы из состоянияiв состояниеjнаk-м шаге, образующих
матрицу
-
вероятности перехода системы из состоянияiв состояниеjнаk-м шаге, образующих
матрицу вероятностей перехода, задаваемую
соответствующим графом переходов
системы из состояния в состояние.
вероятностей перехода, задаваемую
соответствующим графом переходов
системы из состояния в состояние.
Переход из состояния в состояние зависит от того, в каком состоянии находилась система на предыдущем шаге и от Рij(K) - матрицы вероятности переходов наk-ом шаге, и эти вероятности могут меняться. Если матрица вероятности переходов не зависит от номера шага, то цепь Маркова называется однородной.
В основе же прогноза лежит вычисление матрицы переходов, элементами которой являются вероятности перехода прогнозируемых параметров из одного состояния в другое, от одного значения к другому.
