23.Принятие решений по многим критериям: Гарантированные достоинства и недостатки.

Правило использует понятия обобщенных достоинств и недостатков. Это соответствует выделению таких отношений между вариантами, которые показывают, по каким характеристикам один вариант лучше или хуже другого и насколько.

Достоинства и недостатки варианта по каждой характеристике определяются как взвешенная разность логических функций. Исходными данными является таблица μij—логических функций характеристик.

Порядок расчета по данному правилу состоит в следующем:

• для каждого варианта определяются взвешенные разности логических функций по каждой характеристике:

• если разность положительна, то речь идет о достоинстве варианта по данной характеристике. Если разность отрицательна, то речь идет о недостатках варианта по данной характеристике.

Это позволяет разделить достоинства и недостатки вариантов следующим образом.

Достоинства варианта jпо сравнению с вариантомкпоi-ойхарактеристике:

[5.4.1.]

Недостатки варианта jпо сравнению с вариантомкпоi-ойхарактеристике:

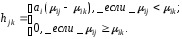
24.Принятие решений по многим критериям: Правило Борда.

Согласно этой процедуре подсчитывается, по скольким парамет­рам данное предложение превосходит все другие, результаты сумми­руются. Лучшей считается предложение, набравшее большую сумму. Эта процедура около двадцати лет применялась при выборах акаде­миков во французской академии наук.

Формально процедуру Борда можно записать следующим обра­зом.

Всем xA (А - множество предложений) припишем значенияr_i(x) определяемым по правилу:

r_i(x) ={bA :Pi(x) <Pi(b)+ε_i}, гдеb - предложения, у которых значениеi-го параметраP_i(b) лучше значенияP_i(x) -i-го параметра предложенияx,s_i - характеристика «чувствительности».

Сумма этих значений образует так называемую шкалу альтерна­тив Борда:

r(x) =

i

Поясним правило примером. Пусть требуется выбрать двигатель для некоторого насоса. Характеристики двигателей показаны в таблице 9.1.

Таблица 9.1

Параметры	Название фирм
	А	B	С	D
Мощность двигателя	25	40	20	30
Расход горючего	30	60	30	45
Вес двигателя	50	80	50	65

По правилу Борда для выбора лучшего двигателя надо использо­вать следующий алгоритм:

• для каждого двигателя подсчитать число параметров, по ко­торым он превосходит остальные двигатели, т.е. определить величи­ну r(x);

• сравнить значения r(x) всех двигателей;

• лучшим считается двигатель, набравший большую сумму.

В нашем примере при допущении ε = 0.00 значения r_i(x) иr(x) показаны в табл. 9.2. По табл. 9.2 лучшим двигателем оказался дви­гатель фирмыA.

25.Принятие решений по многим критериям: Принцип Беллмана-Заде

Многокритериальная оптимизацияилипрограммирование— это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

Задача многокритериальной оптимизации формулируется следующим образом:^[3]

где это() целевых функций. Векторы решенийотносятся к непустой области определения.

Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.

Принятие решения - это выбор альтернативы, которая одновременно удовлетворяет и нечетким целям, и нечетким ограничениям. В этом смысле, цели и ограничения являются симметричными относительно решения, что стирает различия между ними и позволяет представить решение как слияние нечетких целей и ограничений.

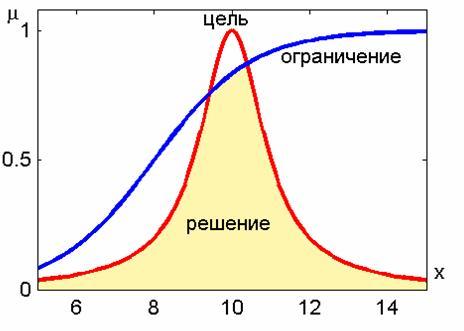
Рис. 14.1 - К примеру 14.1: принятие решения по принципу Беллмана-Заде

При принятии решений по схеме Беллмана-Заде не делается никакого различия между целью и ограничениями. Всякое разделение на цель и ограничения является условным.

Принцип Беллмана-Заде.

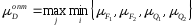
Решение задачи – нечеткое множество (так как с решением соотнесли функцию принадлежности).

По вертикали выполним пересечение множеств. Берем лучшее среди худших. Если два оптимальных решения, то нужно привлекать дополнительную информацию.