19. Многокритериальная оптимизация. Метод идеальной точки.

Многокритериальная оптимизацияилипрограммирование— это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

Задача многокритериальной оптимизации формулируется следующим образом:^[3]

где это() целевых функций. Векторы решенийотносятся к непустой области определения.

Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.

Принятие решения - это выбор альтернативы, которая одновременно удовлетворяет и нечетким целям, и нечетким ограничениям. В этом смысле, цели и ограничения являются симметричными относительно решения, что стирает различия между ними и позволяет представить решение как слияние нечетких целей и ограничений.

Метод идеальной точки

Рассмотрим один из методов, использующий множество Парето - метод идеальной точки. Пусть у нас есть некоторое множество е, каждая точка которого описывается двумя функциям U=Ф(х;у) иV⁼Р(х;y)/).(UиV- средние выигрыши игроков А и В соответственно,axиy - вероятности вы­бора стратегий для получения этого выигрыша).

Теперь в данном множестве ε попытаемся найти такую точку, в которой обе функции U иV принимают свои максимальные значе­ния. В общем случае эта точка окажется вне множества ε. То есть, не существует стратегий, при которых оба игрока получат максималь­ный для каждого выигрыш. Точка, в которой функцииUиV достигают своих максимальных значений, называетсяточкой утопии.

Поэтому строится множество Парето и на нем ищется точка, бли­жайшая к точке утопии — идеальная точка (см. рис. 6.2).

Значения функций U иV в идеальной точке и есть оптимальные средние выигрыши для каждого игрока. Пусть Н_A(р, q) и Нв (р, q) — средние выигрыши игроков А и В с платежными матрицами

Ситуация (p*q*) в биматричной игре А и В называется оптимальной по Парето, если из того, что

вытекают равенства:

Р =Р*, q=q*.

То есть, в оптимальной по Парето ситуации игроки не могут совместными усилиями увеличить выигрыш одного из игроков, не уменьшив при этом выигрыш другого.

20. Принятие решений по многим критериям: Метод последовательных уступок

Руководитель устанавливает СППР (Система поддержки принятия решений) порядок приоритета логических функций, ставя на первое место наиболее важную, и СППР выполняет сл. операции:

СППР находит =, где-значение логической функции по самой важной характеристике, ее индексi=1,j- номер альтернативы.

Руководитель определяет величину уступки

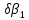
СППР в пределах уступки находит=

Если таких вариантов нет – руководитель увеличивает уступку и в ее пределах СППР выбирает вариант, имеющий максимум по третьей логической функции и.т.д до полного перебора всех .

Такой способ построения компромиссного решения имеет то преимущество, что руководитель имеет возможность наглядно видеть цену (уступки) по каждому критерию.

Процедура получения компромиссного решения может быть реализована и без назначения уступок 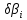. В этом случае вначале отбирают варианты решений по первому (наиболее важному) критерию, затем среди отобранных решений выбираются наилучшие решения по второму критерию и.т.д. Процедура завершается при выборе наилучшего решения по последнему критерию.

Если же методом последовательных уступок решается многокритериальная оптимизационная задача, то к исходным ограничениям задачи на каждом шаге добавляются ограничения вида: