Л.В. АРНОЛЬД, В. С. МАРКОВ,

В. М. СЕЛIIВЕРСТ0В, П. П. ФЕДОРКО

СБОРНИК ЗАДАЧ

по

ТЕХНИЧЕСКОЙ ТЕРМОДИНАМИКЕ

И ТЕПЛОПЕРЕДАЧЕ

ПОД ОБЩЕЙ РЕДАКЦИЕЙ

проф. Л. В. АРЛНОЛЬДА

Допущено

Управлением кадров и учебных заведений

МРФ РСФСР в качестве учебного пособия

для ИНСТИТУТОВ водного транспорта

ИЗДАТЕЛЬСТВО

ЛЕНИНГРАДСКОЕ Отъеление

Ленинград 1960

ЧАСТЬ ПЕРВАЯ

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА

РАЗДЕЛ ПЕРВЫЙ

ПАРАМЕТРЫ ТЕРМОДИНАМИЧЕСКОГО СОСТОЯНИЯ ТЕЛА

Удельный объем газа определяется по формуле

где V– объем рассматриваемого газа в м³;G– его вес в кг.

Удельный вес газа

Давление. Абсолютное давление выше атмосферного определяется как

Здесь: Р_изб- избыточное (или манометрическое) давление;

Р_разреж- показание вакуумметра (вакуум или разрежение);

Р_бар- атмосферное (или барометрическое) давление.

Соотношение между различными единицами давления:

1 ат = 1 кг/см²= 10000 кг/м²= 10000 мм вод. ст. = 735,6 мм рт. ст.

Избыточное давление, выраженное в технических атмосферах, обозначают ати, а абсолютное давление ата.

Пример. Барометр показывает 744 мм рт. ст. Определить абсолютное давление в конденсаторе паровой турбины, если вакуумметр показывает разрежение = 660 мм рт. ст.

Решение. Абсолютное давление в конденсаторе можно определить, воспользовавшись соотношением

Задачи

1. В пусковом баллоне двигателя внутреннего сгорания емкостью 300 л при некоторых температуре и давлении содержится воздух, удельный вес которого 28,6 кг/м³Определить вес воздуха, заключенного в баллоне.

Ответ: G= 8,58 кг.

2. Определить объем 10 кг кислорода, если известно, что его удельный вес равен 1,43 кг/м³

Ответ: V= 7 м³

3. Определить объем 3 кг газа, если известно, что его удельный объем равен 0,74 м³

Ответ: V= 2,22 м³

4. Объем баллона 80 л. Определить вес кислорода, находящегося в баллоне, если его удельный объем равен 0,0128 м³

Ответ: G= 6,25 кг.

5. Манометр показывает давление в воздухопроводе 760 мм вод. ст. при барометрическом давлении 745 мм рт. ст. При другом наблюдении давление в воздухопроводе составляет 600 мм вод. ст., а барометрическое 757 мм рт. ст. Определить, в каком случае абсолютное давление больше и насколько.

Ответ: В обоих случаях абсолютные давления одинаковы и составляют Р_абс= 1,09 ата.

6. Избыточное давление в воздухопроводе равно 500 мм вод. ст. Показание ртутного барометра составляет 760 мм рт. ст. Определить абсолютное давление в воздухопроводе.

Ответ: р = 1,083 ата.

7. Тягомер, соединенный с газоходом котла, показывает разрежение 30 мм вод. ст. Определить абсолютное давление дымовых газов в технических атмосферах, если барометр показывает 750 мм рт. ст.

Ответ: р = 1,017 ата.

8. К дымоходу котла присоединяется тягомер (Креля) с наклонной под углом α=30° трубкой. Тягомер заполнен керосином с удельным весом 0,8 г/см³. Отсчет по длине трубки составляет 180 мм (рис. 1). Какое давление в дымоходе, если барометр показывает 740 мм рт. ст.?

Ответ: р = 0,998 ата.

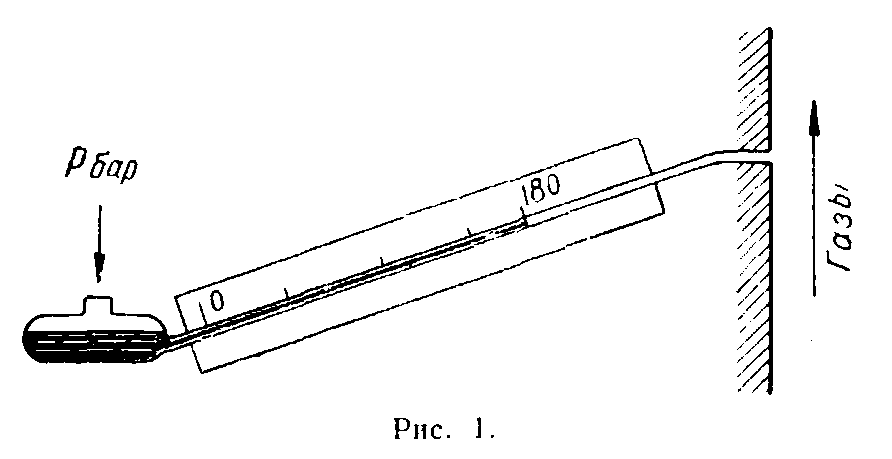
9. Определить абсолютное давление в конденсаторе паровой машины, если вакуумметр показывает разрежение 60 см рт. ст., а показание барометра составляет 750 мм рт. ст.

Ответ: р = 0,204 ата.

10. Определить показания вакуумметра конденсатора паровой машины, шкала которого имеет обозначения в см рт. ст., если при показании барометра 757 мм рт. ст. абсолютное давление в конденсаторе равно 0,3 ата.

Ответ: р_разр= 54см рт. ст.

11. В машинно-котельном отделении судна давление по водяному манометру составляет 120 мм вод. ст. Барометр на палубе показывает 750 мм рт. ст. Стрелка манометра котла указывает 30 ати. Разрежение в конденсаторе по вакуумметру соста вляет 610 мм рт. ст. Определить абсолютное давление:

а) в машинно-котепьном отделении,

б) в котле

в) в кондепсаторе.

Ответ: а) Р_МКО= 1,03 ата;

б) Р_к= 31 ата;

в) Р_конд= 0,2 ата.

12. Ввиду вредного влияния, оказываемого ртутными парами на человеческпй организм, поверх ртути в манометр наливается вода (рис 2). Определить абсолютное давление в воздухопроводе р, если в манометре высота ртутного столба h_р= 450 мм, высота столба водыh_l= 100 мм и давление окружающего воздуха Р_бар= 740 мм рт. ст.

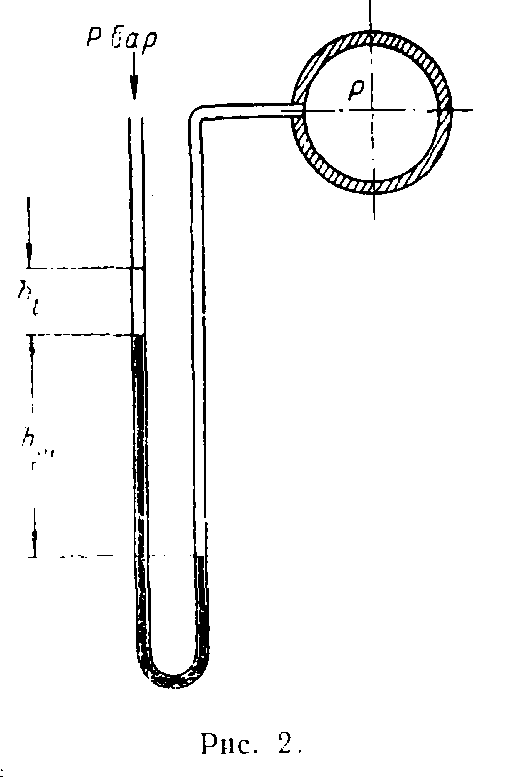
Ответ: р = 1,63 ата

13. На дно цистерны для жидкого топлива помещен колокол А (рис. 3). Воздух под колоколом А сжимается столбом жидкости высотой Н. Давление под колоколом по манометру Р_ман= 150 мм рт. ст. Какова высота Н, если удельный вес топлива равен 0,88 г/см³?

Ответ: Н = 2,32 м.

РАЗДЕЛ ВТОРОЙ

ОСНОВНЫЕ ЗАКОНЫ ДЛЯ ИДЕАЛЬНЫХ ГАЗОВ

Ураваение состояния идеального газа получено в результате совместного использования закона Бойля—Мариотта (приt=const) и закона Гей—Люссака (приv=const). Уравнение состояния имеет вид:

для 1 кг газа

для Gкг газа

Для М молей газа

при М = 1, т.е. для одного моля газа

З а к о н А в о г а д р о позволяет определить объем моля V_μ. При нормальных физических условиях (t= 0°С, р = 760 мм рт. ст.) объем моля любого идеального газа равен 22,4 нм³/моль.

Удельный вес газа γ₀(при (t= 0°Cи р = 760 мм рт. ст.) определяется по формуле

.

где μ — молекулярный вес.

Газовая постоянная Rможет быть определена по формуле

или

Пример. Чему равно давление в резервуаре, содержащем 10,5 нм³водорода при температуре 25°С? Объем резервуара равен 0,5 м³.

Р е ш е н и е. Вес водорода

где γ₀ = 0,09 кг/нм³— удельный вес водорода при нормальных физических условиях.

Давление водорода находим из уравнения

где R= 420,5 кгм/кг град — газовая постоянная водорода.

Пример. Смесь из 0,8 моля аммиака и 0,4 моля азота находится

под давлением 3 ата при температуре 45°С. Какой объем занимает

смесь?

Р е ш е н и е. По уравнению состояния

,

где - объем М молей газа.

М=0,8+0,4=1,2 моля.

Таким образом

.

Пример. Чему равен удельный вес кислорода при 12 ата и 60°С, если при 3 ата и 10°С его удельный вес равен 4 кг/м³?

Р е ш е н и е. Запишем уравнение для двух заданных состояний газа: для состояния 1 (р₁= 3 ата,t₁= 10°С) и для состояния 2 (р₂= 12 ата,t₂= 60°С).

Поделив почленно первое уравяение на второе, получим соотношение

;

.

Поделив почленно первое уравнение на второе, получим соотношение

,

из которого определяем вес газа γ₂

.

Пример. Баллон с воздухом при давлении 125 ата и температуре 25°С весит 36,12 кг. в результате выпуска части воздуха вес баллона уменьшился и стал равным 35,21 кг. Давление воздуха в баллоне при этом снизилось до 90 ата, а температура—до 15°С. Чему будет равно давление в баллоне при температуре 25°С, если из него выпустить еще 0,5 кг воздуха?

Р е ш е н и е. Вес баллона с воздухом равен

вес баллона с воздухом после выпуска первой порцин воздуха равен

где G_б— вес самого баллона, аV— его емкость. Исключая из этих двух уравненийG_б, находим

Отсюда находим емкость баллона

Вес воздуха в баллоне после выпуска части воздуха

Вес воздуха в баллоне после дополиительного выпуска 0,5 кг

Давление воздуха в баллоне в этом случае

Задачи

14. Вычислить удельный вес при нормальных физических условиях водорода; кислорода; азота; метана.

Ответ: γ₀= 0,0899; 1,429; 1,250; 0,717 кг/нм³

15. Определить, чему равен вес 3 нм³воздуха.

Ответ: G= 3,879 кг.

16. Чему равно давление в баллоне, содержащем 0,2 нм³кислорода при 0°С? Объем баллона 50 л.

Ответ: Р = 4,135 ата.

17. Какой объем занимает 6,5 кг кислорода при давлении 40 ата и температуре 20°С?

Ответ: V=0,126 м³

18. При какой температуре 0,4 кг метана занимают объем 50 л при давлении 12 ати, если барометрическое давление равно 755 мм рт. ст.?

Ответ: t= 36°С.

19. В резервуаре находится воздух при температуре — 15°С. Вакуумметр показывает разрежение 200 мм рт. ст. Определить вес воздуха в резервуаре, если объем резервуара равен 2 м³. Барометрическое давление равно 740 мм рт. ст.

Ответ: G=1,94 кг.

20. Какое давление будет показывать манометр, установленный на баллоне емкостью 40 л, если баллон наполнить 0,9 нм³азота при температуре 20°С? Барометрическое давление равно 765 мм рт.ст.

Ответ: р = 23,55 ати.

21. Какой объем занимает 1 моль водорода при давлении 20 ата в температуре 60°С?

Ответ: V= 1,41 м³

22. В резервуаре емкостью 10 м³находится 2 моля ацетилена при температуре —10°С. Под каким давлением находится газ?

Ответ: р = 4,46 ата.

23. В резервуаре объемом 40 м³находится 2,5 моля азота при температуре 27°С. Под каким давлением находится газ?

Ответ: р = 15,9 ата.

24. В резервуаре емкостью 20 м³находится смесь газов, состоящая из 0,6 моля углекислоты и 1,3 моля азота. Давление смеси по манометру равно 1,5 ати. Чему равна температура смеси? Барометрическое давление равно 745 мм рт. ст.

Ответ: t =38°С.

25. Чему равен удельный вес метана, находящегося в баллоне при давлении 65 ата и температуре 40°С?

Ответ: γ = 39,35 кг/м³

26. При какой температуре удельный вес воздуха равен 1,85 кг/м³если давление воздуха равно 2 ата?

Ответ: t== 96°С.

27. Два баллона одинаковой емкости заполнены одинаковым весовым количеством различных газов: метана и кислорода. Температура обоих газов одинакова. Одинаково ли давление в баллонах?

Ответ: Давление в баллоне, содержащем метан, приблизительно в 2 раза меньше, чем в баллоне, содержащем кислород.

28. Чему равен объем азота при давлении 6 ата и температуре 40°С, если при 20 ата н 0°С он равен 3 м³?

Ответ: V=11 ,47 м³

29. Как изменится удельный вес воздуха, если абсолютное давление воздуха возрастет в 2 раза, а температура повысится от 5 до 100 °С?

Ответ: Увеличится в 1,49 раза.

30. Чему равен удельный вес кислорода при давлении 14 ата н температуре 80°С, если при 760 мм рт.ст. и 0°С он равен 1,429 кг/нм³?

Ответ: γ = 14,95 кг/м³

31. Определить удельный вес гелия при давлении 4 ата и температуре 17°С, если известно, что при 1,5 ата и 0°С его удельный вес равен 0,259 кг/м³

Ответ: γ = 0,65 кг/м³

32. Определить подъемную силу воздушного шара, наполненного гелием, если объем шара равен 500 м³, а давление и температура окружающего воздуха (и гелия в воздушном шаре) соответственно равны 600 мм рт. ст. и —25° С.

У к а з а н и е: Подъемная сила воздушного шара равна разности весов газа, наполняющего шар, и окружающего воздуха в объеме шара.

Ответ: G= 485 кг.

33. Подъемная сила воздушного шара, наполненного водородом, при температуре окружающего воздуха —20°С равна 300 кг. Шар внезапно попадает в зону более теплого воздуха с температурой +20°С при том же давлении. Как изменится подъемная сила шара, если считать, что вследствие медленного протекания процесса теплообмена температура водорода не успеет измениться?

Ответ: ∆G=G₂-G₁= -21,2 кг.

34. Чему равна подъемная сила воздушного шара, заполненного 1,5 кг водорода, при давлении 0,6 ата и температуре -30° С? Какой объем должен иметь воздушный шар, заполненный гелием, чтобы его подъемная сила при тех же услонiюях была такой же?

Ответ: G= 20,1 кг;V_He= 27,7 м

35. Воздушный шар объемом 1600 м³, имеющий жесткую оболочку. наполняется нагретым воздухом при атмосферном давлении, после чего его оболочка герметически закрывается. До какой температуры должен быть нагрет воздух, чтобы воздушный шар мог подняться на высоту 2000 м, где атмосферное давление равно 640 мм рт.ст., а температура воздуха 5°С? Вес шара вместе с полезной нагрузкой составляет 0,4 т. Атмосферное давление у поверхности земли равно 760 мм рт. ст.

Ответ: t = 158°С.

36. В баллоне, находящемся при температуре —15°С, Давление равно 42 ати. Как изменится давление в баллоне после того, как его перенесут в помещение, где температура равна 30°С? Барометрическое давление равно 750 мм рт. ст.

Ответ: р = 49,5 ати.

37. По трубопроводу протекает 4 м³кислорода при давлении 1,5 ата и температуре 17°С. Какое весовое количество газа протекает в течение 20 мин.?

Ответ: G= 156 кг.

38. При определении теплоты сгорания топлива калориметрическую бомбу, в которой находится навеска топлива, заполняют кислородом при давлении 20 ати. Кислород в бомбу поступает из баллона. Чему будет равно давление кислорода в баллоне после 130 опытов, если его начальное давление равно 110 ати при температуре 20°С? Объем баллона 40 л, объем калориметрической бомбы 0,3 л. Барометрическое давление равно 750 мм рт. ст. Учесть, что перед заполнением кислородом бомба содержит воздух при атмосферном давлении, условно считая при этом, что подаваемый в бомбу кислород не смешивается с находящимся там воздухом.

Ответ: р = 90,5 ати.

39. Из баллона емкостью 60 л выпустили часть содержащегося там метана, в результате чего давление газа в баллоне уменьшилось от 60 до 23 ата, а температура — от 30° до 10°С. Определить вес выпущенного газа.

Ответ: G= 1,325 кг.

40. 3а какое время компрессор, всасsваюoий 3 м³воздуха, заполнит резервуар емкостью 1,5 м до давления 4 ати? Температура воздуха в резервуаре при этом повышается от 10 до 70°С. Барометрическое давление 765 мм рт. ст.

Ответ: τ = 1,49 мин.

41. В баллоне емкостью 20 л находится 2,1 нм³азота при температуре 20°С. Какое весовое количество газа выпущено из баллона, если его давление понизилось в 2 раза, а температура снизилась до 5°С?

Ответ: G= 1,24 кг.

42. Какую производительность должен иметь компрессор, чтобы давление воздуха в резервуаре емкостью 2,6 м³повысилось от 7 ата до 23 ата в течение 50 мин.? Температура воздуха равна 15°С, ее изменением при работе компрессора превебречь. Барометрическое давление равно 740 мм рт. ст.

Ответ: V= 0,834 м³

43. Производительность компрессора при 1 ата и 10°С 250 м³/час. За какое время он наполнит воздухом резервуар емкостью 25 м³до давления 5 ати, если начальное давление воздуха в резервуаре равно 0,5 ати, а его температура за время наполнения равна температуре окружающей среды (10°С)? Барометрическое давление равно 736 мм рт. ст.

Ответ: τ = 27,2 мин.

44. Сосуд, заполненный атмосферным воздухом (р₀= 1,02 ата,t₀= 17°С), нагревают до 400°С, после чего разобщают с атмосферой и охлаждают. Какое давление установится в сосуде, когда температура воздуха в нем станет равной первоначальному значению? Какое количество воздуха вытекло из сосуда при его нагревании? Объем сосуда равен 2 м³

Ответ: р₂= 0,44 ата;G =1,37 кг.

45. Баллон, содержащий кислород под давлением 130 ата, весит 35,1 кг. В результате выпуска части газа вес баллона стал равным 33,2 кг. Давление в баллоне при этом снизилось до 75 ата. Чему будет равно давление в баллоне, если из него выпустить еще 0,85 кг кислорода? Температура газа во всех указанных случаях остается одинаковой и равна 15°С.

Ответ: Р = 50,4 ата.

РАЗДЕЛ ТРЕТИЙ

СМЕСИ ИДЕАЛЬНЫХ ГАЗОВ

Давление смеси газов равно сумме парциальных давлений компонентов смеси (закон Дальтона):

Объем смеси газов равен сумме парциальных объемов, т. е. объемов отдельных компонентов, приведенных к давлению и температуре смеси:

Для газовой смеси справедливо уравнение состояния идеального газа, если в него вводится газовая постоянная смеси

Состав газовой смеси может быть задан:

а) весовыми долями – g₁,g₂,…,g_n;

б) объемными долями – r₁,r₂,….,r_n;

Объемные доли могут быть также найдены как отношение числа молей компонента к общему гислу молей всей смеси:

В табл. 1 дана сводка основных формул, применяемых в расчетах по газовым смесям.

Пример. Дымовые газы, уходящие из котла, имеют следующий состав по объему: СО₂= 14,5%; О₂= 4,5%; СО = 2,0%;N₂= 79,0%. Определить весовые доли, газовую постоянную, кажущийся молекулярный вес и удельный вес дымовых газов при температуре 220°С и давлении 716 мм рт. ст.

Р е ш е н и е. Определяем кажущийся молекулярвый вес смеси газов по формуле

Весовой состав дымовых газов определяем по формуле

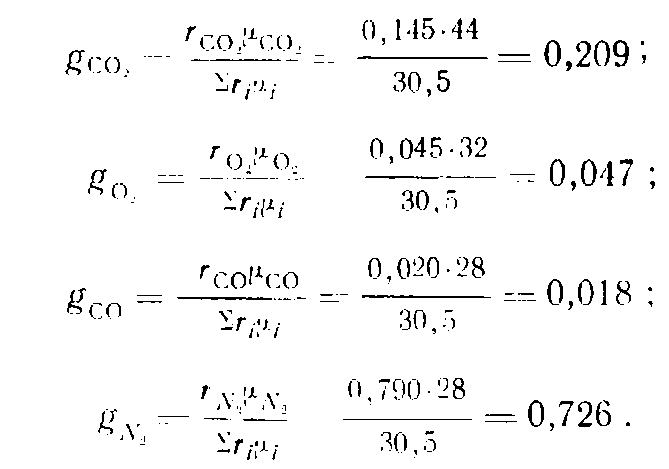
Проверка:

Газовую постоянную дымовых газов определяем из уравнения

газов

Удельный вес дымовых газов

где

Пример. Сухой генераторный газ из антрацита состоит из 12 молей углекислого газа, 64 молей окиси углерода, 24 молей водорода и 120 молей азота. Определить объемные и весовые доли и парциальные объемы компонентов при температуре 27°С и давлении 1,2 ата.

Р е ш е н и е. Объемный состав генераторного газа:

где М — число молей смеси, определяемое как сумма чисел молей компонентов

Определяем кажущийся молекулярный вес смеси

Весовой состав генераторного газа

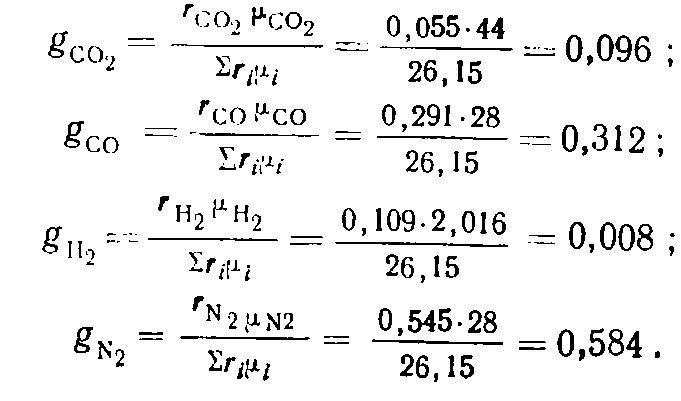
Парциальные объемы компонентов смеси определяем из ураненения

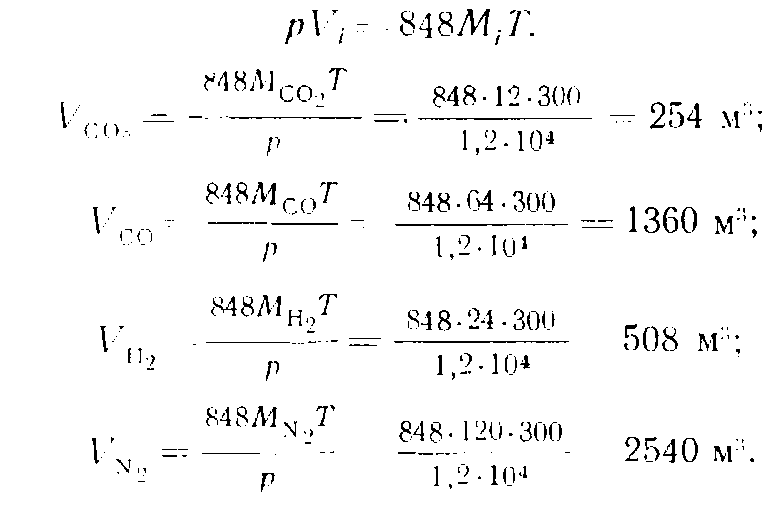
Пример. В сосуде находится смесь кислорода и азота при температуре 50°С. Удельный вес кислорода в смеси 1,81 кг/м³. Определить удельный вес смеси газов и давление, под которым находится смесь, если объемный состав ее:N₂= 40%;O₂= 60%.

Рс ш е н и е. Парциальное давление кислорода определяем по формуле

давление смеси

Газовую постоянную смеси находим но формуле

Удельный вес смеси

Пример. Газовая смесь, состоящая из двух компонентов, находится в сосуде объемом 2 м³под давлением 5 ата при температуре 17°С. Определить вес смеси в сосуде. Определить также, из каких компонентов состоит смесь, если одним из компонентов является окись углерода. Парциальное давление окиси углерода 3 ата. Кажущийся молекулярный вес смеси 17,6.

Р е ш е н и е. Определяем газовую постоянную смеси

Парциальное давление неизвестного газа находим из ураввения

Объемные доли компонентов

Молекулярный вес неизвестного газа может быть определен из уравнения

По значению молекулярного веса определяем, что вторым компонентом смеси является водород.

Вес смеси газов

Задачи

46. Определить весовой состав и вес газовой смеси в баллоне емкостью 33 л, если давление смеси 12 ата, а температура 40°С. Объемный состав смеси: СО₂= 15%;N₂= 83%;O₂= 2%.

Ответ: g(CO₂) = 0,216; g(N₂) = 0,763; g(O₂) = 0,021; G = 0,453 кг,

47. В сосуде объемом 1 м³при давлении 2 ата находится смесь азота и углекислого газа ири температуре 50°С. Вес азота в сосудс 1,5 кг. Определить весовые и объемные доли и вес углекислого газа

Ответ: r(S₂) = 0,735; r(CO₂) = 0.265; g(N₂) = 0.638; g(CO₂) = 0,362; G(CO₂) = 0.85кг

48. Какой объем будут занимать 10 молей газовой смеси, имеющей следующий объемный состав: H₂= 40%; СН₄= 35%; СО = =15%;N₂= 10%, при давлении 3 ата и температуре 90°С. Определить также весовой состав, газовую постоянную и кажущийся молекуляряый вес смеси.

Ответ: V = 102,5 м³; g(H₂) = 0,059; g(CH₄) = 0,418; g(CO) = 0,314; g(N₂) = 0,209;

_c= 13,4;R_c= 63,1 кгм/кг град.

49. Принимая, что сухой воздух состоит из 21 объемной части кислорода и 79 объемных частей азота, определить весовой состав воздуха, его газовую постоянную, кажущпйся молекулярный вес и удельный вес при нормальных физиическпх условнях.

Ответ: g(О₂) = 0,232;g(N₂) = 0,768;R_н= 29,27 кгм/кг град;_н= 29; γ_н= 1,293 кг/им³

50. Какова объемная доля азота в уходящих газах двигателя внутреннего сгорания, если объем остальных составляющих уходящих газов следующий: СO₂= 13%;O₂= 6%; СО = 1%? Определить весовые доли компонентов смеси, газовую постоянную и кажущийся молекулярвый вес уходящих газов.

Ответ: r(N₂) = 0,8;_c= 30,32;R_c= 28 кгм/кг град;g(N₂) = 0,749;g(CO₂) = 0.189;g(O₂) = 0,063;g(CO) = 0,009.

51. Природный газ, имеющий объемный состав СО₂= 2%; СН₄= 93%;N₂= 5%, подается по трубопроводу в газгольдеры, в которых он сохраняется под давлением 1,2 ата ири температуре 25°С. Объем газгольдеров 250 м³. Определить весовоtколичество газа в газгольдерах и удельный вес газа.

Ответ: G= 204 кг, γ_c=0,815 кг/м³

52. Генераторный газ имеет следующий весовой состав: N₂= 62%, СО = 30%, СO₂= 5,5%, Н₂= 2,5%. Определить парциальные давления компонентов смеси и ее удельный вес, если генераторный газ находится под давлением 2,2 ата при температуре 50°С.

Ответ: Р(N₂) = 1,05 ата, Р(СО) = 0,51 ага; Р(СО₂) = 0,06 ата; Р(Н₂) = 0,58 ата; γ_c= 1,73 кг/м³

53. Определить газовую постоянную, удельный вес и удельный объем смеси газов при нормальных физических условиях. если кажущийся молекулярный вес смеси равен 20.

Ответ: R_c= 42,4 кгм/кг град; γ_c= 0.895 кг/нм³; υ_с= 1,12 нм³/кг

54. Определить удельный вес и газовую постоянную сухих дымовых газов после котла при температуре 300°С и разрежении в газоходе 10 мм вод. ст., если их объемный состав следующпй: N₂= 79,5%, СО = 1,5%, СO₂= 13,5%, О₂= 5,5%. Барометрвческое давление равно 745 мм рт. ст. Найти также удельный вес дымовых газов при нормальных физических условииях.

Ответ: γ_c= 0,63 кг/м³;R_c= 27.9 кгм/кг град; γ_н= 1,355 кг/нм³

55. Газовая смесь, состоящая из углекислого газа и азота, имеет кажущийся молекулярпый вес _с= 34. Определить весовой и объемный состав смеси, газовую постоянную и удельный вес смеси при давлении 1,1 ата и температуре 120°С.

Ответ: g(CO₂) = 0,485;g(N₂) = 0,515;r(CO₂) = 0,375;r(N₂) = 0,625;R_c= 24,9 кгм/кг град; γ_c= 1,12 кг/м³

56. Смесь газов состоит по весу из четырех частей воздуха и одной части окиси углерода. Определить весовые и объемные доли, кажущийся молекулярный вес, газовую постоянную, удельный вес и парциальные давления при давлении смеси 1,5 ата и температуре 25°С.

Ответ: g_в= 0,8;g_CO= 0,2;r_в= 0,795;r_СО= 0,205;_с= 28,8;R_c= 29,45 кгм/кг град;

Р_СО= 0,3 ата; Р_в= 1,2 ата; γ_с= 1,705 кг/м³.

57. Смесь азота и углекислого газа при нормальных физических условиях имеет удельный объем 0,65 нм³/кг. Определить объемные и весовые доли компонентов, газовую постоянную и кажущийся молекулярный вес смеси.

Ответ: r(CO₂) = 0,403; r(N₂) = 0,597; g(CO₂) = 0,514; g(N₂) = 0,486;

R_c= 24,7 кгм/кг град;_с= 34,4.

58. Газовая смесь состоит из днух молей углекислоты, двух молей кислорода и четырех молей азота. Определить объемные и весовые доли компонентов, газовую постоянную и кажущийся молекулярный вес смеси.

Ответ: r(CO₂) = 0,25; r(О₂) = 0,25; r(N₂) = 0,50; g(CO₂) = 0,333; g(О₂) = 0,243;

g(N₂) = 0,424;R_c= 25,7 кгм/кг град;_с= 33,0.

59. В цилиндр газового двигателя подается смесь газов. состоящая из одного моля генераторного газа (R_ген= 32 кгм/кг град) и 1,3 моля воздуха. Давление в конце всасывания 0,98 ата температура смеси 80°С. Определить весовое количество смеси, поданной в цилиндр, если диаметр цилиндра 250 мм, ход поршня 340 мм.

Ответ: G= 0,0154 кг.

60. Газовая смесь, состоящая из углеквслого газа, азота и кислорода, находится в резервуаре под давлением 5 ата при температуре 40°С. Парциальные давления компонентов смеси равны: Р(СО₂) == 0,5 ата, Р(N₂) = 3,8 ата. Определить состав смеси в объемных и весовых долях и удельный вес смеси.

Ответ: r(CO₂) = 0,1; r(О₂) = 0,14; r(N₂) = 0,76; g(CO₂) = 0,146; g(О₂) = 0,148;

g(N₂) = 0,706; γ_с= 5,69 кг/м³

61. До какого давления по манометру необходимо сжать газовую смесь, состоящую из 20 кг кислорода, 58 кг азота, 10 кг ‚ углекислого газа и 2 кг сернистого газа, чтобы парциальное давление кислорода в смеси составляло 1,5 ата? Каковы парциальные объемы компонентов при температуре смеси 50ºС? Барометрическое давление воздуха 750 мм рт. ст.

Ответ: р = 6,04 кг/см²;V(С₂) = 2,42 м³;V(СО₂) = 0,88 м3;V(N₂) = 7.96 м3;

V(SO) = 0,12 м³.

62. Определить удельный вес влажного воздуха, рассматривая его как смесь сухого воздуха н водяного пара, при температуре 25ºС и давлении 760 мм рт. ст., если в 1 нм³содержится 8 г водяного нара. Каково парциальное давление водяного нара во влажном воздухе? Водяной пар в данном случае можно считать идеальным газом.

Ответ: γ = 1,18 кг/м³; Р(Н₂О) = 7,3 мм рт. ст.

63. В баллоне емкостью 1 м³находится воздух при давлении 2 ата и температуре 20ºС. Сколько надо накачать в баллон азота, чтобы давление в нем достигло 10 ата при температуре 20°С?

Ответ: G(N₂) = 8,0 кг.

64. Газовая смесь, состоящая из азота и кислорода, находится в баллоне под давлением 2,5 ата при температуре 27°С. Определить состав смеси в весовых долях и парциальные давления компонентов, если удельный вес смеси при заданных условиях равен 2,91 кг/м³.

Ответ: g(N₂) = 0,575;g(O₂) = 0,425;P(N₂) = 1.52 ата;P(О₂) = 0,98 ата.

65. В сосуде объемом 2 м³находится 5 кг воздуха при температуре 40°С. В сосуд введено 2 кг углекислого газа. Определить объемные и весовые доли после введения углекислого газа. Насколько возросло давление в сосуде?

Ответ: g(O₂) = 0,166; g(N₂) = 0,548; g(CO₂) = 0,286; r(O₂) = 0,166; r(N₂) = 0,626;

r(CO₂) = 0,208; ∆р = 0,295 ата.

РАЗДЕЛ ЧЕТВЕРТЫЙ

ТЕПЛОЕМКОСТЬ ИДЕАЛЬНЫХ ГАЗОВ

В зависимости от выбранной единицы измерения количества вещества различают:

сккал/кг град — весовую теплоемкость, т. е. теплоемкость, отнесенную к 1 кг рабочего тела;

Сккал/нм³град – объемную теплоемкость, т.е. теплоемкость, отнесенную к 1 нм³(или γ₀кг) рабочего тела;

сккал/моль град — мольную теплоемкость, т. е. теплоемкость, отнесенную к одному молю (кг или 22,4 нм³) рабочего тела.

Указанные теплоемкости связаны между собой следующими зависмосгями:

где — молекулярный вес и γ₀кг/нм³— удельный вес газа при нормальных физических условиях.

Количество тепла, сообщаемое рабочему телу, зависит от особенностей протекания термодинамического процесса, а поэтому и теплоемкость рабочего тела также зависит от процесса. Особоважными являются и з о х о р н а я (в процессе при v=const) теплоемкосгь С_vи и з о б а р н а я (в процессе при р =const) теплоемкосгь С_р.

Для газов:

ккал/кг град

В общем случае теплоемкость газа зависит от температуры. В связи с этим различают истинную и среднюю теплоемкость. Среднюю Теплоемкость в интервале температур от t₁доt₂обозначают , а в интервале от 0ºС доt, ради сокращения письма, обозначают просто. В технических расчетах главным образом приходится иметь дело со средней теплоемкостью. Связь между средней и истинной теплоемкостью при температуреtв обшем виде выражается формулой

Зависимость теплосмкости от температуры достаточно сложна (криволинейная зависимость). Обычно пользуются таблицами теплоемкостей. (см. Приложения 2) В таблицах даны значения средней теплоемкости в интервале от 0°С до t, т. е. величина. Для определения средней теплоемкости в интервале отt₁доt₂используется формула

где и— средние теплоемкости соответственно в интервале температур от 0°С доt₁и от 0°С доt₂.

Поскольку теплоемкость является слабой функцией температуры, в ряде случаев возможна замена криволинейной зависимости теплоемкости на линейную (с некоторой допустимой погрешностью). В этом случае теплоемкость выражается функцией вида

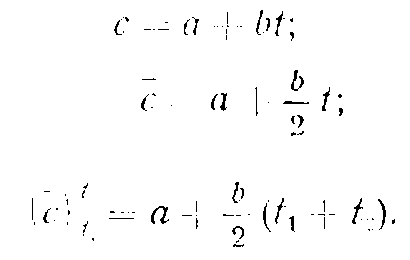
Для средней мольной изобарной теплоемкости (в пределах от 0° до 1500°С) могут быть использованы формулы:

для кислорода (О₂)

для азота (N₂)

для воздуха

для окиси углерода (СО₂)

для водяного пара (Н₂О) (рассматривается как идеальный газ)

для углекислого газа (СО₂) от 0° до 600°С

В том случае, когда теплоемкость газа изменяется в сравнительно небольших пределах (t₂–t₁<100°C) (данное указание не распространяется на область температур, меньших 0°С), можно принять среднюю теплоемкость постоянной н равной ее значению при любой из температур в интервале отt₁доt₂. При приближенных расчетах обычно полагают теплоемкость постоянной и равной ее значению при 0°С. В этом случае значения мольных теплоемкостей могут быть взяты по данным табл. 2.

Теплоемкость смеся газов в зависимости от способа задания состава смеси определяется по одной из следующих формул:

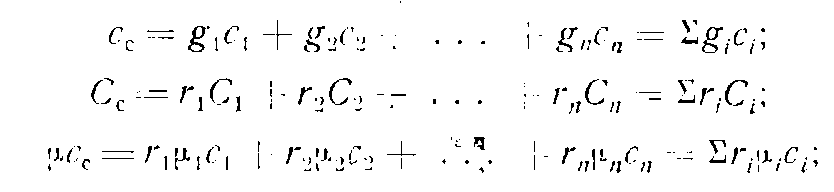
где g₁,g₂….g_n— весовые доли компонентов смеси;

r₁,r₂…r_n- объемные доли компонентов смеси;

c_c — теплоемкость смеси.

Количество тепла, участвующего в процессе, определяется по формуле

Пример. Определить значение объемной теплоемкости N₂при постоянном давления, считая, что теплоемкость газа не зависит от температуры.

Р е ш е н н е. Для двухатомных газов с_р= 6,95 ккал/моль град.

Следовательно

Пример. Определить количество тепла, отдаваемое 1 им³дымового газа при его охлаждении от 1300° до 300°С. Объемный состав газа

r(CO₂)=12%; r(H₂O)=7%; r(N₂)=75%; r(O₂)=6%. При расчете принять криволинейную зависимость теплоемкости от температуры. Процесс охлаждения считать протекающим при р =const.

Р е ш е н и е. Определяем количество тепла по формуле

где и— средняя объемная теплоемкость смеси газов соответственно в итервале от 0° до 300°С и от 0° до 1300°С. Теплоемкость

Количество отданного тепла

Пример. Используя формулу для средней мольной изобарной теплоемкости окиси углерода, найти истинную изохорную объемную теплоемкость при 1000°С.

Р е ш е н и е. Если средняя мольная изобарная теплоемкость

то истинная мольвая теплоемкость будет

Пользуясь формулой для теплоемкостгi

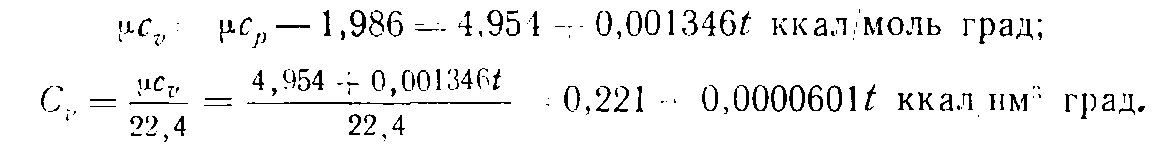
При t= 1000°С получим

Пример. Определить истинную весовую изобарную теплоемкость воздуха при 1500°С, пользуясь таблицей средних теплоемкостей.

Р е ш е н и е. Принимаем

Из таблиц

Задачи

66. Определить обьемную теплоемкость кислорода при постоянном давлении, считая ее независящей от температуры.

Ответ: С_р= 0,310 ккал/нм³град.

67. Вычпслить среднюю теплоемкость воздуха в интервале температур от 200 до 800°С при постоянном давлении, считая зависимость теплоемкости от температуры криволинейной.

Ответ: = 0,260 ккал/кг град.

68. Определить истинную изобарную весовую теплоемкость кислорода при t=1000°С, если= 0,2206 + 0,000254t

Ответ: 0,2714 ккал/кг град.

69. Найти объемную изобарную теплоемкость окиси углерода, если известно, что = 0,248 ккал/кг град.

Ответ: С_р= 0,310 ккал/нм³град.

70. Найти весовуно теплоемкость азота при постоянном давлении, если известно, что для азота R= 30,25 кгм/кг град и С_р= 0,181 ккал/кг град.

Ответ: С_р= 0,252 ккал/кг град.

71. Определить среднюю весовую теплоемкость азота при постоянном давлении в пределах от 250° до 1200°С, считая зависимость теплоемкости от темпсратуры

а) криволинейной,

б) прямолинейной.

Ответ: а) = 0,257 ккал/кг град;

б) = 0,279 ккал/кг град.

72. Используя формулу для средней мольной изобарной теплоемкости кислорода дать зависимость объемной изохорной истинной теплоемкости от температуры и определить С_рприt= 500°С.

Ответ: С_р= 0,226+0,0000726t; С_t=500= 0,2623 ккал/нм³град.

73. Определить истинную объемную теплоемкость кислорода при постоянном объеме при 1200°С, пользуясь таблицей средних теплоемкостей

Ответ: = 0,301 ккал/нм³град.

74. Определить истиную изобарную объемную теплоемкость смеси газов при t=320°С. Состав смеси в объемных долях:r(CO₂) = 0,13;r(O₂) = 0,043;r(CO) = 0,007;r(N₂)=0,82.

Ответ: (С_р)_с= 0,332 ккал/нм³град.

75. Определить истинную теплоемкосгь моля продуктов сгорания бензпна ири постоянном давлении, если t=1600°С. Весовой состав продуктов сгорания: 19,0% СО₂, 9,5 Н₂О и 71,5%N₂.

Ответ: (µC_p)_c= 9,768 ккал/моль град.

76. Продукты сгорания 1 кг бензина имеют следующий состав: 0,464 моля двухатомаых газов, 0,071 моля углекислого газа и 0,075 моля паров воды. Определить среднюю мольную изохорную теплоемкость продуктов сгорания от 0 до 1500°С. (Теплоемкость двухатомных газов принять равной теплоемкости азота).

Ответ: = 6,594 ккал/моль град.

77. Для условий предыдущей задачи определить продуктов сгорания.

Ответ: = 8,580 ккал/моль град.

78. Вычислить количество тепла, необходимое для подогрева 1 кг воздуха от 300° до 1200°С. Процесс протекает при постоянном давлении.

Ответ: 244,6 ккал/кг.

79. Через воздухоподогреватель, установленный на паровом котле, проходит 4500 нм³/ч воздуха. Температура воздуха на входе в воздухоподогреватель равна 20°С, а на выходе 200°С. Определить количество тепла, сообщенное воздуху. р =const.

Ответ: Q= 256680 ккал/час (с учетом зависимости теплоемкости от температуры):Q= 251340 ккал/час (считая теплоемкость постоянной).

80. Углекислый газ (СО₂) в количестве 6 кг заключен в баллон при температуре 30°С. Определить: а) количество тепла, сообщенное углеквслому газу при нагревании его до 270°С в процессе при постоянном объеме, приняв зависимость теплоемкости от температуры криволинейной; б) погрешность при определении количества тепла, если привять. С_р= 0,1505+0,00011t(линейная зависимость).

Ответ: а) Q= 261,9 ккал; б)Q= 264,2 ккал; ∆Q= 0,76%.

81. 0,4 м³азота нагрева.тся ог 20 до 470°С при давлении 2,5 ата. Определить: а) Количество тепла, затраченное на нагревание азота, приняв зависимость теплоемкости от температуры криволинейной; б) погрешность при определении количества тепла, если принять теплоемкость постоянной.

Ответ: а) Q= 130,0 ккал; б)Q= 126,2 ккал; ∆Q= -2,70%.

82. Определить количество тепла, необходимое для нагревания 1 нм³воздуха от 200 до 1000°С в процессе при постоянном давлении, приняв криволинейную зависимость теплоемкости от температуры.

Ответ: Q= 274,3 ккал/нм³

83. Для условий задачи 82 определить количество тепла, если процесс протекяет при постоянном объеме.

Ответ: Q= 203,4 ккал/нм³

84. Топочные газы поступают в газоход котла при t₁= 1100°С, а выходят ириt₂= 700°С. Состав газов по объему:r(CO₂) = 13%,r(O₂) = 5%,r(H₂O) = 7%,r(N₂) = 75%. Определить количество тепла, теряемое 1 нм³топочных газов, принимая криволинейную зависимость теплоемкости от температуры. Р =const

Ответ: Q= 158,8 ккал/нм³

85. В составе топочных газов имеется азот. Определить количество тепла, отдаваемого азотом в окружающую среду в течение часа, если расход топочных газов равен 5000 нм³/ч, объемная доля азотаr(N₂) = 0,8, температура топочииьих газовt= 360°С, а температура окружающей среды равна 20°С. При определении количества тепла принять криволинейную зависимость теплоемкосги от температуры. Р =const

Ответ: Q= 428060 ккал/час.

86. Для условий предыдущей задачи вычислить погрешность при определении количества тепла, если принять: а) зависимость теплоемкосги от температуры прямолинейной; б) теплоемкость постоянной.

Ответ: а) ∆Q= + 1,44%; 6) ∆Q= -1,42%.

87. Воздух охлаждается от 800° до 100°С в процессе при постоянном давлении. Определить количество тепла, выделяемого . при охлаждении 1 кг и 1 нм³воздуха.

Ответ: q_g= 180,6 ккал/кг;q_v= 233,4 ккал/нм³

88. При испытании судового двигателя внутреннего сгорания был определен состав продуктов сгорания на 1 кг жидкого топлива: G(CO₂) = 3,18 кг,G(CO) = 0,006 кг,G(N₂) = 18,6 кг,G(O₂) = 2,32 кг,G(Н₂О) = 1,18 кг. Считая давление постоянньим, определйть среднюю весовую теплоемкость продуктов сгорания при температуре газов, равной 420°С.

Ответ: = 0,259 ккал/кг град.

РАЗДЕЛ ПЯТЫЙ

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ

Тепло Qпревращается в механическую работуL(или наоборот) в эквивалентных количествах

Q=AL

где — тепловой эквивалент механической работы.

Тепловые эквиваленты: 1 силочаса: 1 л.с.-ч= = 632 ккал; 1 киловаттчаса: 1 квт-ч = 860 ккал.

Экономический к. п. д. теплового двигателя определяется в зависимости от удельного расхода топлива по очевидной формуле

если удельный расход топлива с_свыражеп в кг/л. с.-ч, или

если удельный расход топлива с_свыражен в кг/квт-ч.

Здесь — теплота сгорания топлива в ккал/кг

В тех случаях, когда по тем или иным причинам можно не учитывать перемещения рабочего тела как целого (например, при неподвижном центре тяжести рабочего тела), аналитическое выражение первого закона термодинамики, отнесенное к 1 кг рабочего тела, имеет вид

dq=du+Adl

или

q=∆u+Al

где qккал/кг — количество тепла, подведенного к рабочему телу (q>0) или отведенного от рабочего тела (q<0);

∆uккал/кг — изменение внутренней энергии рабочего тела;

lкгм/кг — работа, совершаемая рабочим телом. В процессе расширения работаlсчитается положительной, а в процессе сжатия — отрицательной.

для идеального газа изменение внутренней энергии определяется по формуле

где ккал/кг град - средняя весовая изохорная теплоемкость газа в интервале температур отt₁доt₂;

t₁иt₂— начальная и конечная температура газа.

В случае направленного движения (потока) рабочего тела первый закон термодинамики выражается следующим уравнением:

где ∆lккал/кг - изменение удельной энтальпии рабочего тела;

ω₁и ω₂м/сек — начальная и конечная скорость потока;

l_m, кгм/кг — техническая работа, совершаемая потоком рабочего тела. Если стенки, ограничивающие поток рабочего тела, неподвижны, тоl_m= 0.

Для идеального газа изменение энтальпии определяется по формуле

где ккал/кг град - средняя весовая изохорная теплоемкость газа в интервале температур отt₁доt₂;

Связь между энтальпией и внутренней энергией рабочего тела определяется соотношением

или

где риv— давление (кг/м²) и удельный объем (м³/кг) рабочего тела в рассматриваемом состоянии.

Пример. Пассажирский пароход идет со скоростью 20 км/час. Какова мощность силовой установки парохода, если на 1 км пути расходуется 50 кг каменного угля с теплотой сгорания 5000 ккал/кг? К. п. д. силовой установки равен 12%.

Р е ш е н и е. Часовой расход топлива

В=5020=1000 кг/час.

Часовое количество тепла, выделившееся от сгорания 1000 кг/час топлива

Мощность силовой установки

Пример. К воздуху в количестве G=5 кг подведеноQ=20 ккал тепла, в результате чего воздухомcовершена работаL= 5000 кгм. Как при этом изменилась удельная внутренняя энергия воздуха?

Р е ш е н и е. Изменение внутренней энергии 5 кг воздуха

Изменение удельной внутренней энергии составляет:

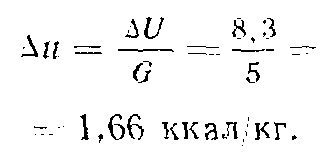
Пример.

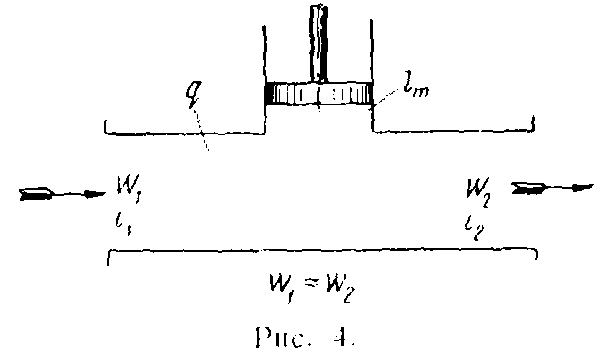
Определить техническую работу, которую может совершить поток газа (рис. 4), если к нему подводится 5 ккал/кг тепла. Энтальпия газа в результате процесса уменьшилась на 15 ккал/кг. Изменением скорости потока можно преаебречь.

Р е ш е н и е. Используя уравнение первого закона термодинамики для потока, определим техническую работу l_mкгм/кг

Задачи(При решении задач настоящего и всех последующих разделов первой части, если не слелано специальной оговорки, значение теплоемкости газа принимается ПОСТОЯННЫМ (не зависящим от температуры) и определяется по мольным значениям теплоемкостей)

89. Определить, какое количество тепла может быть получено от 1 г урана в атомном котле (реакторе), если для силовой установки мощностью 75 000 л. с. требуется 140 г урана в сутки при к. п. д. котла (реактора) 40%. Сколько бы потребовалось в сутки угля с теплотой сгорания 7000 ккал/кг для этой же силовой установки?

Ответ: q_ур= 2,03510⁷ккал/г; В’ = 4.0710⁵кг/сутки.

90. Пассажирский поезд, совершающий рейсы между Москвой и Ленинградом (расстояние приблизительно 650 км), идет со скоростью 65 км/час. Мощность силовой установки 2500 л. с., а ее к. п. д. 10%. Какое количество топлива необходимо взять на паровоз, чтобы его хватило на весь рейс? Теплота сгорания топлива 10000 ккал /кг

Ответ: В’ = 15 800 кг.

91. При стендовых испытаниях двигателя внутреннего сгорания его приходится затормаживать. Для этого используется гидротормоз. Во избежание нагрева тормозного устройства его охлаждают водой. Определить, какая доля тепла уносится с охлаждающей водой, если мощность двигателя 300 л. с., часовой расход воды 3000 кг/час. Начальная температура воды 15°С, конечная 60°С.

Ответ: 71%.

92. Определить экономический к. п. д. двигателя мощностью 50 л. с., если расход бензина на 1 км пути составляет 320 г при скорости 40 км/час. Теплота сгорания бензина 10 500 ккал/кг.

Ответ: _э= 0,236

93. Определить количество воды, необходимое для охлаждения цилиндра двигателя нутреннего сгорания, если цилиндровая мощность 100 л.с., КПД двигателя 0,38, а относвтельная потеря тепла с охлаждающей водой в тепловом балансе двигателя состав ляет 0,28. Тсмпература охлаждающей воды на входе 15°, на выходе 60°С. (Во всех задачах теплота воды принимается равной 1 ккал/кг град.)

Ответ: G= 1035 кг/час.

94. Удельный расход пара па паровую турбину составляет 2,75 кг/л.c. час. Начальная энтальпия нара 750 ккал/кг.Определить, какое количество тепла теряется с отработавшим паром.

Ответ: q_пот= 520 ккал/кг.

95. При работе двигателя 30% от всего тепла топлива передается охлаждающей воде. К. п. д. двигателя 0,30. Определить количество охлаждающей воды, цвркулирующей в двигателе на 1 л. с., если подогрев воды составляет 40°С.

Ответ: g= 15,8 кг/л. с. час.

96. За какое время 2,5 л воды нагреются до температуры кипения с помощью электрического кипятильника мощностью 450 вт? Теплообмен с внешней средой отсутствует. Начальная температура воды равна 20°С.

Ответ: τ = 31 мин.

97. Вследствие плохой смазки машины происходит нагревание 150 кг стали за 30 мин. на 50°С. Определить вызванную этим потерю мощности машины. Теплоемкость стали 0,11 ккал/кг град.

Ответ: 2,62 л. с.

98. Через какое время в закрытом помещешюи объемом 25 м³температура достигает 25°С в случае его отопления электронагревателем мощностью 0,8 квт? Коэффициент использования вагревателя 0,7. Начальная температура воздуха в помещении 10°С, а потери в окружающую среду составляют 20%. Начальное давление воздуха в помещении 760 мм рт. ст.

Ответ: 12 мин.

99. Определить мощность, удельный расход топлива и КПД двигателя, если при его испытании с помощью гндротормоза получены следующие результаты: крутящий момент М_кр= 95,5 кгм, число оборотовn= 1500 об/мин и часовой расход топлива В = 36 кг/час. Теплота сгорания топлива 10000 ккал/кг.

Ответ: N= 200 л.с.;_э= 0,35; с_е= 0,18 кг/л. с.-ч.

100. Определить давление вала на подшипник, если часовой расход воды на его охлаждение составляет 100 кг/час, а повышение температуры воды 40°С. Число оборотов вала n= 300 об/мин, диаметр вала 110 мм. Коэффициент трения 0,1.

Ответ: Р = 2740 кг.

101. Первый искусственный спутник Земли был создан и запущен на орбиту в СССР. При выходе на орбиту искусственный спутник движется со скоростью 29 000 км/час. Через некоторое время после запуска скорость спутника уменьшается, спутник входит в более плотные слои атмосферы и сгорает. Определить, какое количество тепла разовьется на 1 кг тела спутника при снижении его скорости до 20 000 км/час.

Ответ: q= 4080 ккал/кг.

102. К 3 кг окиси углерода подведено 10 ккал тепла, в результате чего газом совершена работа 6000 кгм. Определить, как изменилась температура газа. Теплоемкость газа считать постоянной.

Ответ: ∆t= —7,5°С.

103. К 2 кг кислорода подведено 70 ккал тепла. Определить, какое количество тепла пошло на изменение внутренней энергии и на внешнюю работу, если в результате совершения термодинамического процесса температура газа возросла от 10° до 166°С.

Ответ: ∆U= 50 ккал;L= 8540 кгм.

104. При движении газа через проточную часть турбины совершается техническая работа в 20 000 кгм/кг и в то же время от газа отведено 5 ккал/кг тепла. Определить снижение температуры газа в турбине. Работой сил тяжести и изменением скорости газа пренебречь. Теплоемкость газа считать ПОСТОЯННОЙ и равной 0,24 ккал/кг град.

Ответ: ∆t= 216°С.

105. Определить значение энтальпии 1 кг воздуха, если 5 кг воздуха при давлении 20 ата занимают объем 280 л. Условно принять, что при 0°С энтальпия равна нулю.

Ответ: i = 26,3 ккал/кг.

106. Определить изменение внутренней энергии и энтальпии 5 кг азота, если температура азота возросла от 100° до 300°С. Учесть зависимость теплоемкости от температуры.

Ответ: ∆U= 180 ккал; ∆I= 250 ккал.

107. Принимая потери в вентиляторе равными нулю, определить энергию, переданную потоку воздуха в вентилятореi(техническая работа, отнесенная к 1 кг воздуха; см. рис. 5). Разрежение воздуха во всасывающем патрубке равно р₁= —10 мм вод. ст., скорость воздуха ω₁= 40 м/сек. В нагнетательном патрубке давление воздуха р₂= 75 мм вод. ст., скорость ω₂= 50 м/сек. Температура воздуха в помещении 20°С, барометрическое давление 745 мм рт. ст. Удельный вес воздуха принимается постоянным.

Ответ: l_m= 117,8 кгм/кг.

108. Центробежный вентилятор подает в топку парового котла воздух в количестве 6500 м³/час при температуре 30°С и давлении 150 мм вод. ст. Барометрическое давление 760 мм рт. ст. Диаметр выходного патрубка вентилятора 300 мм. Определить мощность, потребляемую вентилятором, если его к. п. д. 0,7.

Ответ: N= 6,5 л. с.

РАЗДЕЛ ШЕСТОЙ

ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ

С ИДЕАЛЬНЫМИ ГАЗАМИ

Термодинамический процесс, описываемый уравнением

где n— произвольное, но постоянное число, называется п о л и т р о п н ы м процессом, а числоnназывается п о к а з а т е л е м п о л и т р о п ы.

В том случае, когда теплоемкость может быть принятой не зависящей от температуры, политропный процесс можно определить как процесс, протекающий при неизменном в течение процесса значении теплоемкости с, определяемой по формуле

где

с_р– изобарная теплоемкость газа;

c_v– изохорная теплоемкость газа.

Частными случаями политропньгх процессов являются:

а) процесс, протекающий при постоянном объеме (и з о х о р н ы й);

б) процесс, протекающий при постоянном давлении (и з о б а р н ы й);

в) процесс, протекающий при постоянной температуре (и з о т е р м и ч е с к и й);

г) процесс, протекающий без теплообмена с внешней средой (а д и а б а т н ы й).

Уравнения, устанавливающие связь между начальными и конечными параметрами газа, а также основные формулы для определения работы и тепла, участвующих в процессе, приведены в табл. 3.

В таблице приведены формулы для 1 кг идеального газа. Если же в процессе участвуют Gкг газа, то работа в тепло, участвующие в процессе вычисляются по формулам

и

В том случае, когда теплоемкость можно принять не зависящей от температуры, при протекании политропного процесса соотношение между изменением внутренней энергии, работой и теплом, участвующими в процессе, остается постоянным на протяжении всего процесса. Поэтому отношение изменения внутренней энергии к теплу, участвующему в процессе, есть однозначная функция показателя политропьгn. Значение х определяется по формуле

Таким образом

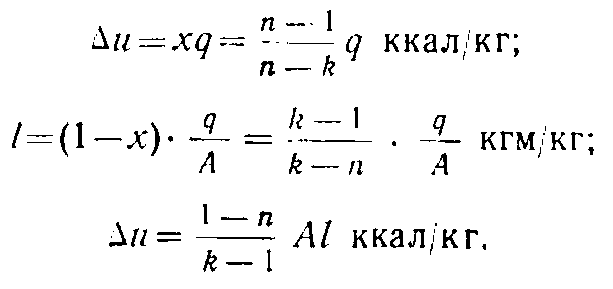
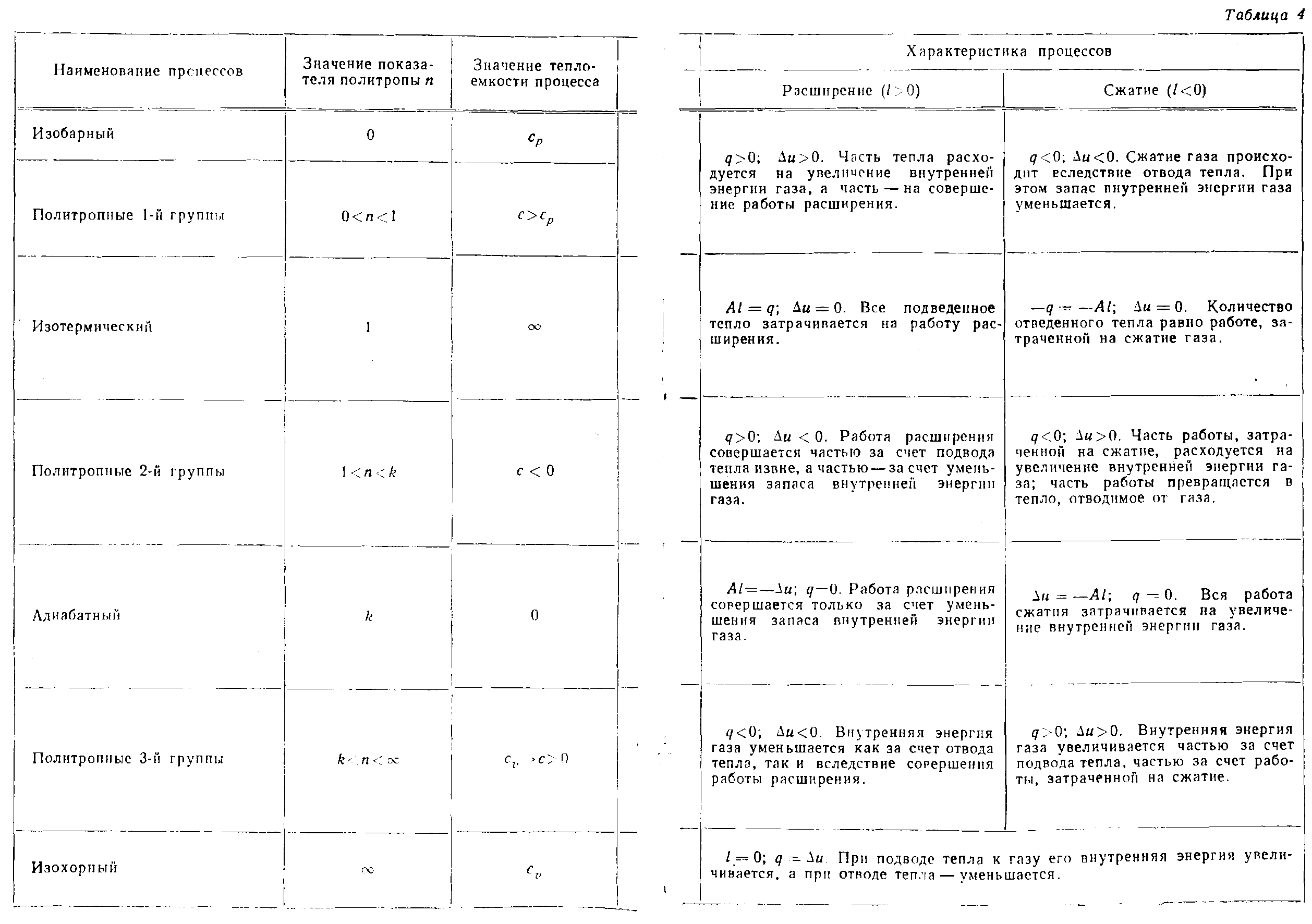
В зависимости от значения n(или х) политропные процессы разделяются на три группы:

1-я группа: 0<n<l;

2-я группа: l<n<k;

3-я группа: k<n<∞.

Х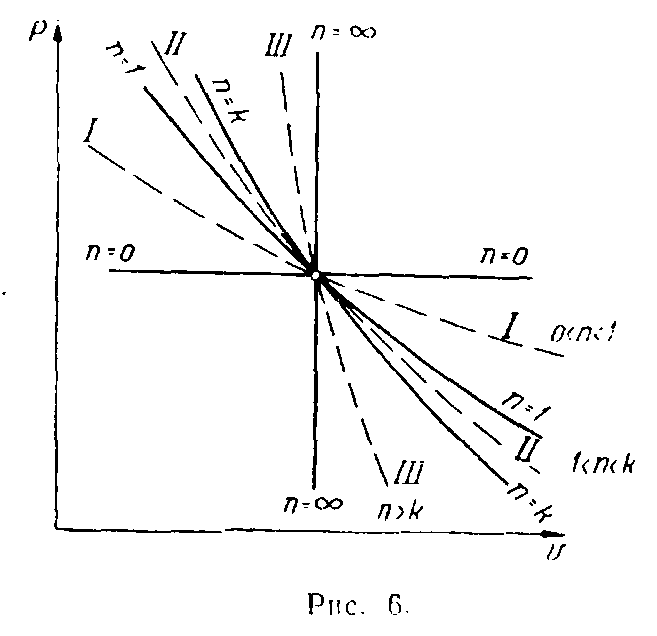арактеристика политропных процессов различных групп приведена в табл. 4, а схематическое изображение их взаимного расположения в диаграмме рvприведено на рис. 6

Пример. При изохорном отводе 60 ккал тепла от 1 нм³азота давление газа понижается от 30 ата до 15 ата. Определить конечную температуру газа. Теплоемкость считать постоянной.

Решение. Количество тепла, участвующее в процессе, определяется по формуле

Объемная изохорная теплоемкость азота равна

Так как

получим

Отсюда искомая температура определяется как

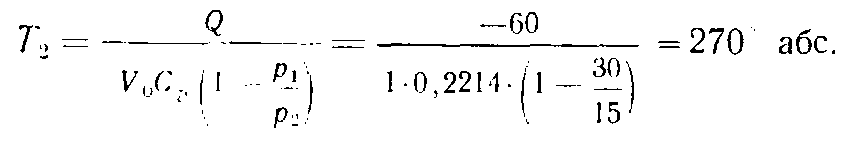
Пример. К 2 кг воздуха изохорно подведено 59,85 ккал тепла. Определить конечное давление воздуха, если его начальное давление равно 1,5 ата, а начальная температура равна 25°С. Зависимость теплоемкости от температуры считать криволинейной.

Р е ш е н и е. После того как будет определена конечная температура воздуха, его конечное давление можно будет найти из соотношения между параметрами в изохорном процессе

Конечную температуру можно определить из выражения для тепла, подведенного в изохорном процессе

Поскольку значение конечной температуры, необходимое для нахождения средней теплоемкости, неизвестно, задачу следует решать методом последовательных приближений.

В первом приближении полагаем, что теплоемкость газа постоянна и равна

Тогда

Зная значение t₂, по таблицам теплоемкостей (приложение 5) определим значение средней теплоемкости

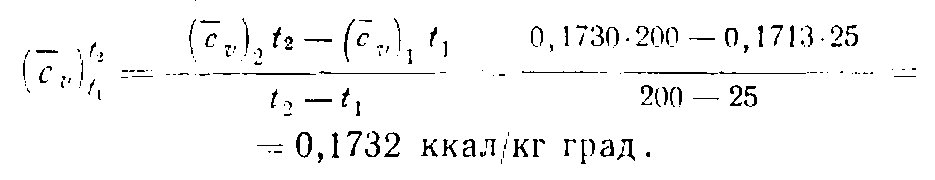
Находим температуру t₂во втором приближении

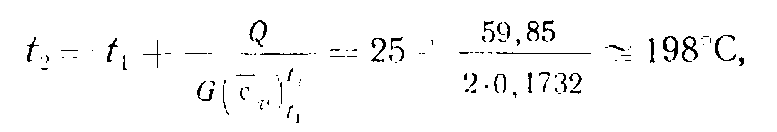
что отличается от значения t₂, найденного в первом приближении, всего на 2ºС. Поэтому можно остановиться на этом значенииt₂. (Если бы оказалось, что значениеt₂, полученное во ВТОРОМ приближении, значительно отличается от предыдушего, следовало бы таким же образом найти значениеt₂в третьем приближении и т. д., пока, наконец, полученное значениеt₂будет близко к полученному в предыдущем приближении. Тогда для дальнейших расчетов принимается значение, полученное в последнем приближении).

Определяем конечное давление воздуха

Пример. 1 кг азота охлаждается при v= 0,75 м3/кг =constдо температуры —40°С, а затем изобарно нагревается до начальной температуры. Определить начальное давление газа, если известно, что при нагревании к газу было подведено на 12 ккал больше, чем отведено при охлаждении.

Р е ш е н и е. Изобразим процесс в координатах рv(рис. 7).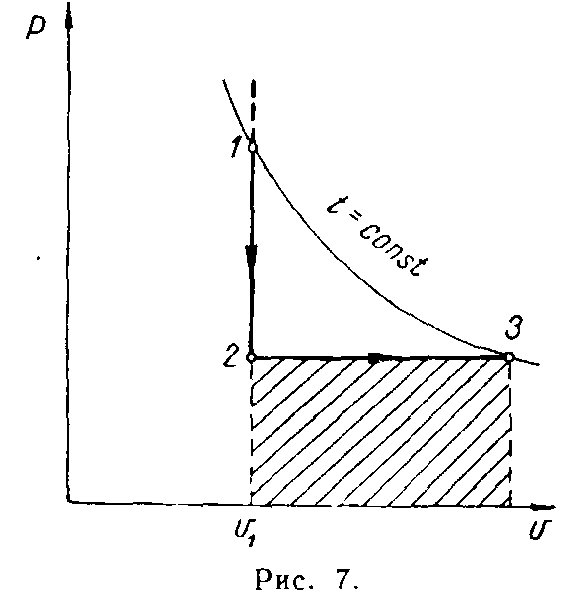Так как температуры в точках 1 и З одинаковы (t₁=t₃), а точка 2 общая для обоих процессов, то изменение внутренней энергии газа в обоих процессах по абсолютной величине Одинаково (Но противоположно по

знаку) |u₂-u₁| = |u₃-u₂|

Разность между абсолютными значениями подведенного и от веденного тепла, равная 12 Ккал/кг, есть та часть тепла, которая израсходована на совершение работы при изобарном расширении. Таким образом

Это позволяет определить начальную температуру t₁=t₃.

Начальное давление газа определяется из уравнения состояния

Пример. На изобарное сжатие 1 кг кислорода затрачена работа 10 000 кгм, после чего газ изотермическ расширяется. Определить давление газа в конце изотермического расширения, если работа расширения равна работе изобарного сжатия. В начале сжатия объем газа равен 0,4 м3/кг. Температура газа в конце расширения равна 30° С.

Р е ш е н и е. Изобразим процесс в координатах рv(рис. 8).

для определения конечного давления газа необходимо знать давление в точке 2:p₂=p₁. Последнее может быть определено следующим образом.

Из выражения для работы газа в изобарном процессе

можно найти начальную температуру газаt₁. При этом имеется в виду, чтоt₂=t₃= 30ºC.

Из уравнения состояния идеального газа определяем давление в точке 1

Из выражения для работы в изотермическом процессе находим

С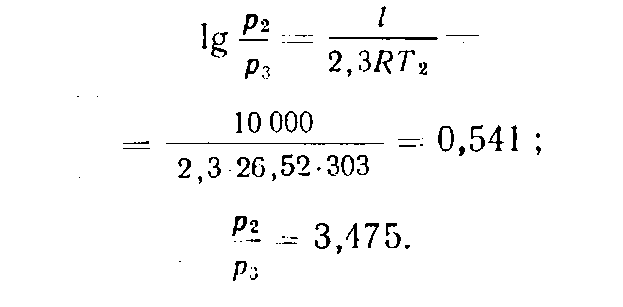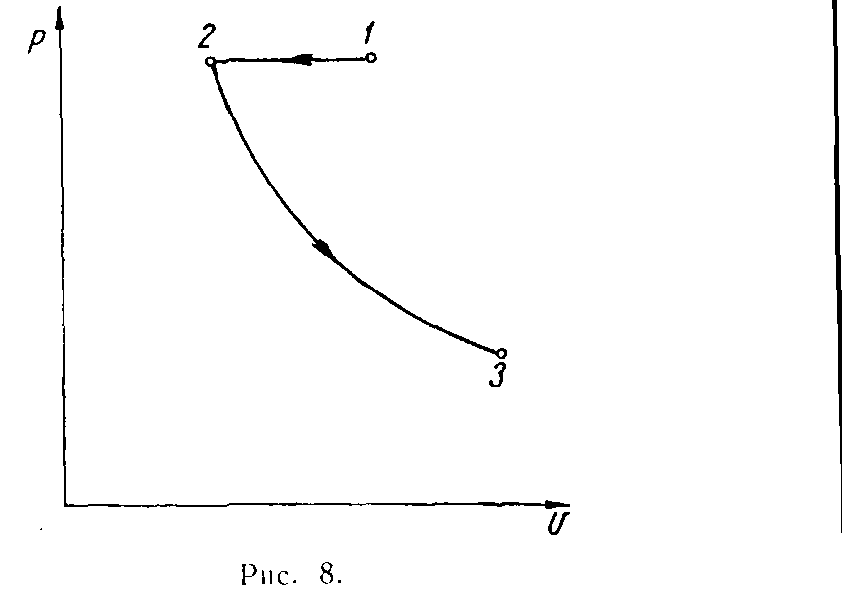ледователбно

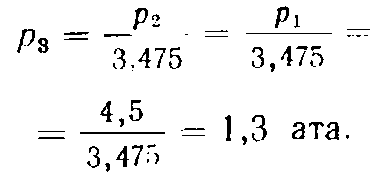
Пример. Из сосуда, содержащего воздух при давлении 14 ата и температуре 80С, вытекает одна треть содержимого. Определить давление и температуру оставшегося воздуха в конце истечения, принимая истечение происходящим без теплообмена с внешней средой.

Р е ш е н н е. Вследствие вытекания части Воздуха другая его часть, остающаяся в сосуде, расширяется, причем по условиям задачи это расширение происходит адиабатно. Удельный объем воздуха в сосуде до истечения равен , а после истечения(ЗдесьG₁иG₂- вес воздуха в сосуде до и после истечения части воздуха,V– объём в сосуда). По условиям задачипоэтому

Конечное давление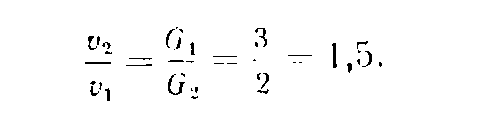

Конечная температура

Пример. Какое количество тепла необходимо изобарно подвести к З кг окиси углерода (СО), чтобы при последующем адиабатном расширении газ мог быть приведён в состояние p₃= 2 ата,v₃= 1,2 м³/ кг? Начальное состояние газа характеризуется параметрамиp₁= 5,5 ата,v₁= 0,19 м³/кг. Теплоёмкость считать постоянной.

Р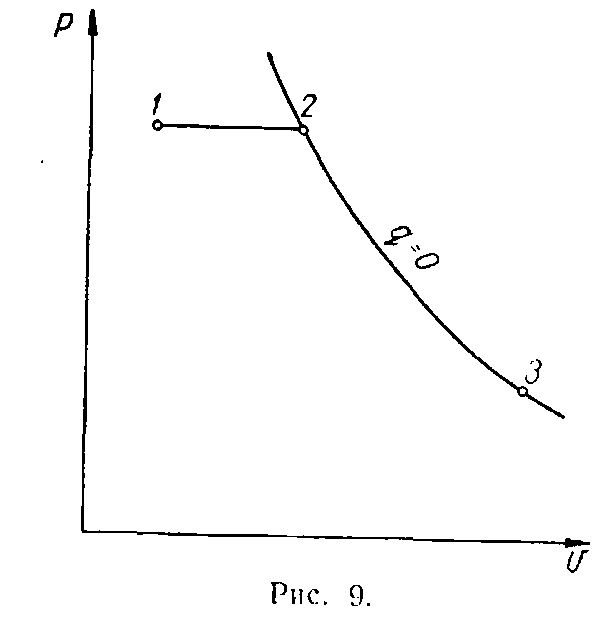ешение. Изобразим процесс в координатахpv( рис. 9). Точка 2, соответствующая состоянию газа в конце изобарного расширения, должна находиться на адиабате, проходящей через точку 3 (p₃= 2 ата,v₃= 1,2 м³/кг). Поэтому удельный объём в точке 2 можно определить как

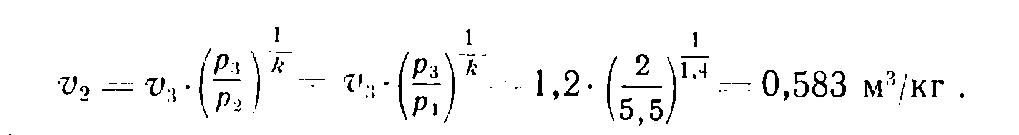
Так как v₂>v₁, в изобарном процессе 1—2 тепло подводится, как это и указывается в уcловиях задачи. В случаеv₂<v₁ имело бы место изобарное сжатие, т. е. отвод тепла.

Температура газа в начале и в конце изобарного расширения определяется из уравнения состояния

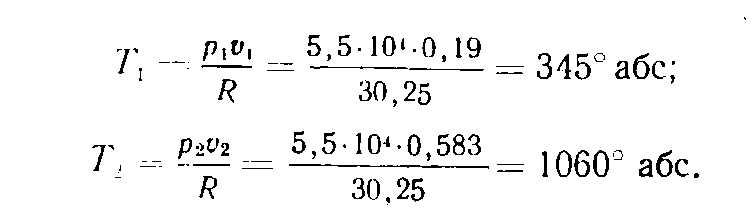
где – весовая изобарная теплоёмкость окиси углерода.

П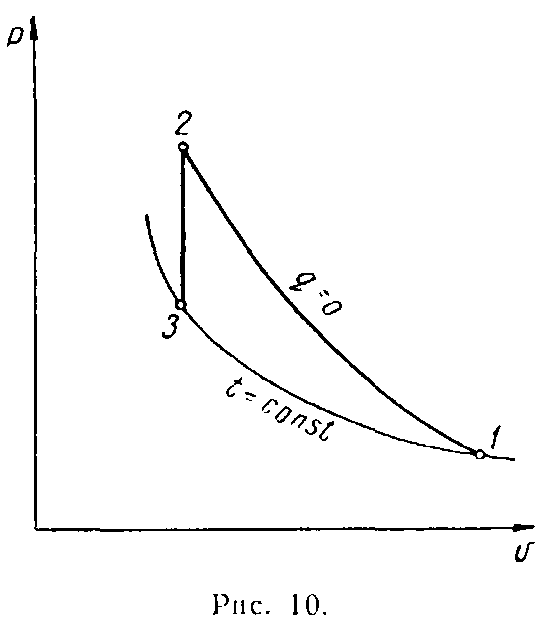ример. Вследствие адиабатного сжатия 0,6 нм³воздуха его температура повышается до 310°С, а давление — до 30 ата; при этом на сжатие воздуха затрачена работа 16 000 кгм. Затем воздух изохорно охлаждается до начальной температуры. Определить конечное давление воздуха и количество отведённого тепла. Теплоёмкость считать постоянной.

Решение. Изобразим процесс в координатах рv (рис. 10). Количество тепла, отведённого в изохорном процессе, равно уменьшению внутренней энергии газа. Работа адиабатного сжатия расходуется на увеличение внутренней энергии газа. Но в рассматриваемом случае ввиду того, что температура в точках 1 и 3 одинакова, а точка 2 является общей для обоих процессов, изменение внутренней энергии в обоих процессах – в адиабатном 1 – 2 и в изохорном 2 – 3 – одинаково по величине, но противоположно по знаку. Поэтому количество отведённого тепла можно определить как

Объемная изохорная теплоемкость воздуха

Конечная температура газа определяется из формулы

откуда

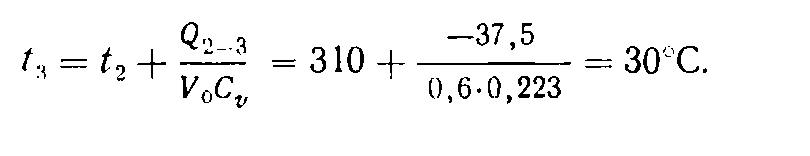
Конечное давление воздуха определяется из соотношения между параметрами газа в изохорном процессе

Пример. Исследовать процесс политропного расширения азота при показателе политропы равном 1,2.

Р е ш е н и е. Отношение изменения внутренней энергии газа

к теплу, участвующему в процессе, равно

Отношение работы процесса к теплу, участвующему в процессе

При расширении газа его работа положительна: Al>0. Так каки А1>0, тоq>0, т. е. в рассматриваемом процессе имеет место подвод тепла к газу. Так какq>0 и, то ∆u<0, т. е. внутренняя энергия газа уменьшается. Таким образом, в исследуемом процессе работа расширения производится как за счет уменьшения запаса внутренней энергии газа, так и за счет подвода к газу тепла извне.

Отношение равно 2, откуда заключаем, что за счет подведенного извне тепла совершается 50% работы. Следовательно, за счет внутренней энергии газа совершается также 50% работы.

Энергетические преобразования в рассматриваемом процессе можно схематически представить так (такую схему называют схемой трансформации энергии):

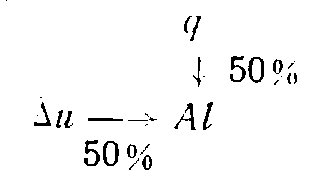
Пример. На сжатие 0,7 нм³аргона затрачена работа 12 000 кгм, при этом от газа отведено 8 ккал тепла. Во сколько раз увеличилось давление газа? Как изменилась энтальпия газа? Начальная температура газа равна 12°С. Теплоемкость считать постоянной.

Р е ш е н и е. Из соотношения

получаем значение n

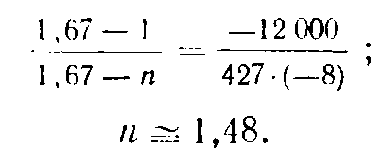
Объемная изохорная теплоемкость аргона равна

Политропна я (объемная) теплоемкость процесса

Из выражения для определения количества тепла

определим конечную температуру газа

Изменение энтальпии газа

Отношение конечного давления к начальному

т. е. давление газа увеличилось в 5.72 раза

Задачи

109. В баллоне находится кислород под давлением 64 ата при температуре —30°С. Как изменится давление газа в баллоне, если Температура увеличится до 25° С?

Ответ: Р₂= 78,5 ата.

110. В закрытом резервуаре находится воздух при разрежении 20 мм рт. ст. и температуре 35° С. До какой температуры следует охладить газ, чтобы разрежение в резервуаре стало равным 100 мм рт. ст.? Барометрическое давление 765 мм рт. ст.

Ответ: t₂= -2ºС.

111. В результате охлаждения метана, находящегося в закрытом баллоне емкостью 40 л при давлении 60 ата, его давление снизилось до 55 ата. Определить количество отведенного тепла. Теплоемкость считать постоянной. Начальная температура газа равна 40ºС.

Ответ: Q= —14,1 ккал

112. Какое количество тепла необходимо подвести к азоту. находящемуся в баллоне емкостью 20 л при давлении 25 ата и температуре 15 ºС, чтобы давление газа увеличилось До 29 ата? Теплоемкость газа считать постоянной.

Ответ: Q= 4,7 ккал.

113. 2 кг смеси газов, состоящей по объему из 14% СО₂, 5% О₂, 2% СО и 79%N₂, находятся под давлением 0.5 ати при температуре 200°С. Сколько тепла должно быть отведено изохорно, чтобы давление газа уменьшилось до 0,17 ати? Принять криволинейную зависимость теплоемкости от температуры. Барометрическое давление равно 770 мм рт. ст.

Ответ: Q= —36,5 ккал

114. В цилиндре двигателя внутреннего сгорания происходит изохорный подвод тепла к рабочему телу, заполняющему объем камеры сгорания, равный 0,2 л, в результате чего давление рабочего тела повышается от 32 ата до 68 ата. Определить количество подведенного тепла, если начальная температура рабочего тела равна 380°С. Рабочее тело обладает свойствами воздуха. Теплоемкость считать постоянной.

Ответ: Q= 0,423 ккал.

115. В Двигателе внутреннего сгорания к рабочему телу изохорно подводится 180 ккал/кг тепла. При этом давление рабочего тела возрастает от 30 ата до 70 ата. Определить конечную температуру рабочего тела. Рабочее тело обладает свойствами воздуха. Теплоемкость считать постоянной.

Ответ: t₂= 1553° С.

116. К 1 кг кислорода изохорно подводится 15,9 ккал тепла, в результате чего давление газа возрастает до 3,8 ата. Определить начальное давление кислорода, если его начальная температура равна 0°С. Принять зависимость теплоемкости от температуры прямолинейной.

Ответ: р₁= 2,88 ата.

117. От 3 кг окиси углерода изохорно отводится 107 ккал тепла. Определить конечное Давление газа, если его начальное давление равно 60 ата, а начальная температура равна 400°С. Зависимость теплоемкости от температуры считать криволинейной.

Ответ: р₂= 43 ата.

118. Определить работу, совершаемую ири изобарном расширении 2,5 кг углеквслоты до двойного объема, если начальная температура газа равна 45° С.

Ответ: L= 15 300 к гм.

119. При совершении изобарного сжатия 1 кг азота при давлении 2 ата от газа отводится 17,5 ккал тепла. Определить конечную температуру и объем газа, а также изменение его внутренней энергии. Начальная температура газа равна 135° С. Теплоемкость считать постоянной.

120. Какую работу производит при изобарном расширении 3,7 нм³окиси углерода, если энтальпия газа увеличивается на 68 ккал/кг?

121. При изобарном сжатии 2 кг кислорода объем газа уменьшился в 1,3 раза, а внутренняя энергия газа уменьшилась на 16,4 ккал/кг. Начальный объем газа равен 0,6 м³Определить давление газа. Теплоемкость считать постоянной.

Ответ: р = 4,05 ата.

122. В газоходах парового котла движутся дымовые газы, имеющие следующий состав по объему: СО₂= 10,3%; О₂= 7,8%;N₂= 75,3%; Н₂О = 6,6%. Определить количество тепла, отдаваемое 1 нм³дымовых газов на участке газохода, на котором температура газов снижается от 800° до 400° С. Определить также, как изменится скорость газов, если сечение газохода по всему данному участку одинаково. Учесть зависимость тенлоемкости от температуры, считая ее криволинейной.

123. 2 кг газовой смеси изобарно нагреваются от 400° до 1800°С. Определить количество подведенного тепла и работу, совершаемую смесью газов, если смесь имеет следующий весовой состав: СО₂= 14%; О₂= 6%;N₂= 75%; Н₂О = 5%. Теплоемкость считать постоянной.

Ответ: G= 697 ккал;L= 82 250 кгм.

124. Какое количество азота необходимо взять, чтобы при изобарном расширении от 100 до 700 °С газ совершил работу 25000 кгм? Как при этом изменится энтальпия газа? Какое количество водорода необходимо взять для совершения такой же работы в том же температурном интервале? Принять прямолинейную зависимость теплоемкости от температуры.

Ответ: G(N₂) = 1,376 кг;i= 156,55 ккал/кг;G(H₂) = 0,099 кг.

125. 1 кг гелия изобарно охлаждается так, что его объем уменьшается в 1,6 раза, а затем изохорно нагревается до первоначальной температуры. Определить конечное давление газа и совершаемую работу, если начальное давление равно 2 ата, а начальная температура равна 210°С.

Ответ: р₁= 3,2 ата;L= 400 кгм/кг.

126. После изобарного расширения 1 кг окиси углерода происходит его изохорное охлаждение до начальной температуры. При этом при нагревании газ получает на 15 ккал тепла больше, чем отдает при охлаждении. Определить конечное давление газа, если известно, что начальный объем газа равен 0,9 м³/кг, а максимальное значение температуры в описанном процессе составляет 250° С

Ответ: р₂= 0,63 ата.

127. При сжатии 2,3 кг воздуха его объем уменьшился в 4 раза. Начальная температура воздуха 30° С, начальное давление 1,05 ата. Какое количество тепла должно быть отведено от газа, чтобы его температура оставалась постоянной? Определить также конечное давление воздуха.

Ответ: Q= -66,1 ккал; р₁= 4,2 ата.

128. При расширении 0,5 м³ацетилена совершается работа 15 000 кгм. Определить конечное давление газа, если его начальное давление равно 6,5 ата. а температура газа в процессе расширения не изменилась.

Ответ: р₂= 4,1 ата.

129. Как изменится объем гелия в процессе его изотермического расширения при температуре 100° С, если к 2 кг газа подводится 40 ккал тепла?

Ответ: v₂/v₁= 1,11.

130. Какое количество тепла необходимо подвести к кислороду, чтобы объем газа увеличился в 4 раза и стал равным 0,5 м³, а температура газа при этом не изменилась? Начальное давление газа равно 7,5 ата.

Ответ: Q= 30,4 ккал.

131. При изотермическом сжатии воздуха в цилиндре давление увеличивается в 4,5 раза. Какая часть работы сжатия расходуется в течение первой половины хода поршня?

Ответ: L₁/L= 0,328.

132. Какое количество тепла необходимо отвести от 10 кг воздуха, чтобы при уменьшении объема воздуха в 6 раз температура его осталась постоянной и равной 20°С? Чему при этом равна работа сжатия?

Ответ: Q= -359,4 ккал;L= -153460 кгм.

133. На изотермическое сжатие азота от 0,9 ата до 5,4 ата затрачивается работа 12 000 кгм. Определить начальный и конечный объем газа.

Ответ: V₁= 0,745 м³;V₂= 0.124м³

134. Во сколько раз увеличится объем 1 кг метана при изотермическом расширении, если получаемая при этом работа равна работе изотермического расширения 1 кг воздуха при двухкратном увеличении объема? Температура обоих газов одинакова.

Ответ: v₂/v₁= 3,49.

135. Определить работу расширения 2 нм³кислорода от 4 ата до 0,8 ата, если в процессе расширения внутренняя энергия газа остается неизменной, а начальная температура равна 10°С.

Ответ: L= 22 400 кгм

136. Начальное состояние газа определяется параметрами р₁= 10 ата иV₁= 0,8 м³. Построить (с соблюдением масштабов) изотерму расширения, используя графический способ.

137. Построить (с соблюдением масштабов) в координатах рvизотерму сжатия 1 кг азота, используя уравнение изотермы. В начальном состоянии температура газа равна 60° С, а давление равно 2 ата; конечное давленые равно 12 ата.

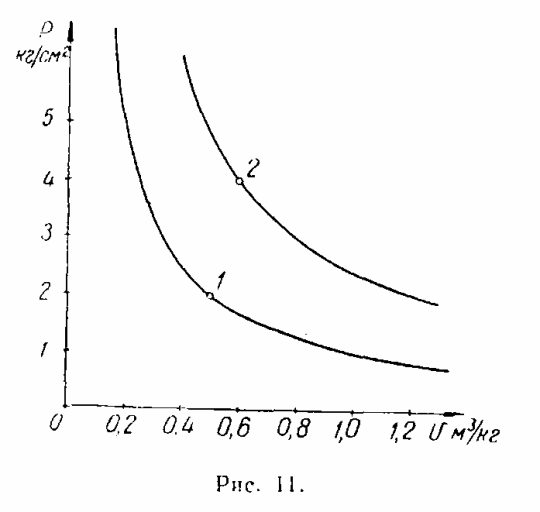
138. Являются ли изотермами линии, изображенные на рис. 11? Определить температуры н точках 1 и 2, если диаграмма построена для а) азота: б) водорода; в) кислорода.

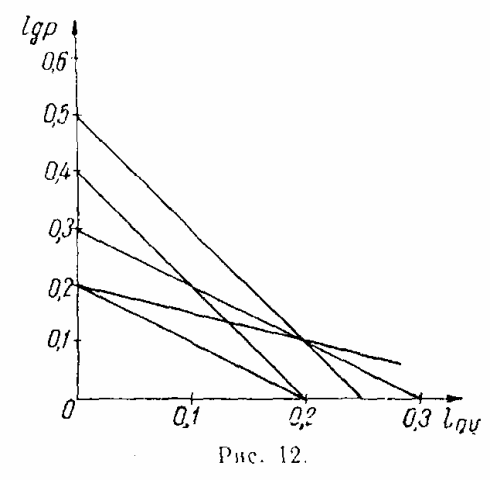
139. Имеются ли среди линий, построенных на рис. 12. изотермы? Для каких температур они построены? График построен для 1 кг воздуха, при его построении давление измерялось в ата, а объем — в м³/кг

140. 1 кг азота изотермически сжимается так, что его объем уменьшается в 2 раза, а затем изобарно расширяется до первоначального объема. Определить конечную температуру газа, а также суммарное изменение внутренней энергии, работу и тепло, участвующие в процессе, если начальная температура газа равна 20° С, а начальное давление равно 1,2 ата.

Ответ: t₂= 313 °С;

u= 52,3 ккал/кг;l= 2720 кгм/кг;

q=58,7 ккал/кг.

141. На изобарное сжатие 0,2 нм³окиси углерода за трачена работа 6000 кгм, после чего газ изотермически расширяется. Определить Давление газа в конце изотермического расширения. если работа расширения равна работе изобарного сжатия. Известно также, что газ в начале сжатия занимает объем 0,085м³, а температура газа в конце расширения равна 20° С.

Ответ: р₃= 0,645 ата.

142. К 4 кт кислорода подведено 68 ккал тепла, причем первые 50% этого тепла подводятся изохорно, а последующие 50% — изотермически. Определить начальное давление газа, если его конечное давление равно 0,8 ата, а конечная температура равна 15° С. Теплоемкость газа считать постоянной.

Ответ: Р₁= 1,045 ата.

143. 1 кг воздуха изотермически расширяется так, что его объем увеличивается в 2,2 раза, выполняя при этом работу 6900 кгм, а затем в изохорном процессе давление воздуха доводится до первоначального значения. Определить конечную температуру воздуха и количество подведенного тепла, если минимальное давление воздуха в описанном процессе составляет 1,1 ата.

Ответ: t₂= 386° С;q= 78,2 ккал/кг.

144. Какую работу необходимо затратить на адиабатное сжатие 0,7 нм³воздуха от 1,3 ата до 18 ата, если начальная температура воздуха равна —15° С?

Ответ: L= — 7700 кгм.

145. Как изменяется давление и температура гелия, если в результате адиабатного сжатия его объем уменьшается в 6 раз?

Ответ: р₂/р₁= 19,8; Т₂/Т₁= 3,3.

146. Во сколько раз уменьшится объем 0,7 кг азота при его адиабатном сжатия, если внутренняя энергия газа увеличивается на 13 ккал/кг, а начальная температура газа равна 0° С?

Ответ: В 2,24 раза.

147. Определить давление я удельный вес азота в конце адиабатного сжатия, если в начале сжатия давление и температура газа равны соответственно 1,3 ата и 12° С, а работа, затраченная на сжатие 1 кг газа, равна 14 000 кгм.

Ответ: Р₂= 7,48 ата;= 5,25 кг/м³

148. Из сосуда, заполненного кислородом при давлении 8 ати и температуре 140° С вытекает одна пятая часть содержимого. Определить давление и температуру оставшейся части кислорода полагая, что процесс, протекающий в сосуде, может рассматриваться как адиабатный. Барометрическое давление 740 мм рт. ст.

Отвел:: Р₂= 5,56 ата; Т₂= 104° С.

149. Работа, полученная при адиабатном расширении 1,5 кг окиси углерода, равна 21 000 кгм. Определить начальное давление газа, если конечное давление р₂= 1 ата, а конечная температура Т₂= 15° С. Определить, на сколько изменилась внутренняя энергия газа в процессе расширения.

Ответ.: Р₁= 5,66 ата;U= —49,6 ккал.

150. В двигателе с воспламенением от сжатия происходит адиабатное сжатие воздуха до температуры, превышающей температуру воспламенения впрыскиваемого топлива. Какова должна быть степень сжатия (отношение объемов в начале и в конце сжатия), если температура воздуха в конце сжатия должна быть равной 700° С? Температура воздуха в начале сжатия равна 100° С. Определить также работу, затрачиваемую на сжатие 1 кг воздуха.

Ответ: а = V₁/V₂>11,0;l= —44 000 кгм кг.

151. Решить предыдущую задачу, учитывая зависимость теплоемкости от температуры и полагая эту зависимость криволинейной.

Ответ: а = V₁/V₂>14,3;l= —48900 кгм/кг.

152. В цилиндре происходит адиабатное сжатие воздуха, начальное давление которого равно 0,95 ата, а начальная температура 25° С. До какого давления можно сжать воздух, если его температура не должна превышать 1700° С? Определить также работу сжатия 1 нм³воздуха.

Ответ: p₂> 3,8 ата;L= —13 700 кгм/нм³

153. Определить работу адиабатного расширения 1 кг метана от Р₁= 10 ата до Р₂= 1,5 ата. Какое количество гелия необходимо взять, чтобы при адиабатном расширении в том же интервале давлений получить ту же работу, что и в случае расширения метана? Сравнить температуры газов в конце расширения. Температура газов в начале расширения одинакова и равна 160° С.

Ответ: l= 26 000 кгм/кг;G_He= 1,42 кг;

= —4°С; 1 = —71° С.

154. В результате сжатия азота его давление повышается в 6,5 раза. Сравнить работу, затрачиваемую на сжатие 1 кг газа, для двух случаев:

а) сжатие происходит изотермически;

б) сжатие происходит адиабатно.

Начальная температура газа в обоих случаях одинакова и равна 25° С.

Ответ: а) 1 = —16 850 кгм/кг;

6)1 = —15 950 кгм/кг.

155. 1 кг водорода адиабатно сжимается от 8 м³до 5 м³, а затем изобарно расширяется до первоначального объема. Определить изменение внутренней энергии, работу и тепло, участвующие в процессе, а также конечное давление и температуру газа. Начальная температура газа равна —30° С.

Ответ: ∆u= 563 ккал/кг; 1 = 22 200 кгм/кг;q= 615 ккал/кг; р₃= 2,46 ата;t₃= = 196° С.

156. Кислород находится в состоянии, которое характеризуется параметрами: Р₁= 2,2 ата,v₁= 1,2 м³/кг Какое количество тепла необходимо изохорно отвести от 3 нм³газа, чтобы последующим адиабатным сжатием газ можно было привести в состояние р₂= 4 ата,v₂= 0,6 м³/кг. Теплоемкость считать постоянной.

Ответ: Q= —208 ккал.

157. К воздуху изобарно подводится некоторое количество тепла, а затем происходит адиабатное расширение воздуха до начальной температуры. В результате этих двух процессов газ совершает работу 42 000 кгм/кг. Начальное состояние воздуха характеризуется параметрами: t₁= 30° С;v₁= 0,09 м³. Определить максимальную температуру воздуха в этом процессе и его конечное давление.

Ответ: t_max= 440° С; Р₂= 0,495 ата.

158. К 1 нм³азота изохорно подводятся 5 ккал тепла, вследствие чего температура газа повышается до 300° С, а давление до 15 ата. В результате последующего адиабатного расширения давление газа уменьшается до первоначального значения. Определить работу, произведенную газом, и его конечную температуру.

Ответ: L = 8700 кгм; t₂= 208° С.

159. К 3,5 кг окиси углерода изохорно подводится 150 ккал тепла, вследствие чего температура газа повышается до 250° С, а давление — до 20 ата. В результате последующего адиабатного расширения температура газа уменьшается до начального значения. Определить работу, произведенную газом, и его конечное давление.

Ответ: L = 63 600 кгм; р₂= 2,33 ата.

160. На сжатие 1 нм³воздуха затрачивается работа, равная 25 000 кгм. Начальные параметры газа: Р₁= 1 ата;t₁= 20° С. Определить давление сжатого воздуха, если сжатие осуществляется:

а) изотермически;

б) адиабатно.

Ответ: а) р₂= 9,65 ата; 6) р₃= 9,5 ата.

161. 1 кг воздуха изотермически расширяется так, что его объем увеличивается в 2 раза, после чего воздух расширяется адиабатно до температуры 15° С. Определить начальное давление воздуха, если его конечное давление равно 1 ата. Начальная температура воздуха 250° С. Вычислить также работу расширения. Как изменилась бы работа расширения, если бы вначале происходило адиабатное расширение, а затем — изотермическое (при тех же начальном в конечном состояниях воздуха)?

Ответ: р₁= 16,2 ата;l= 27 800 кгм/кг;

l= — 4750 кгм/кг.

162. Построить график зависимости для воздуха в пределах измененияот 3,0 до 7,0. Здесь: р₁и р₂— давление воздуха в начале и в конце сжатия;L_адиL_изот- работа, затрачиваемая на сжатие одинакового количества воздуха в адиабатном и в изотермическом процессах соответственно.

У к а з а н и е. Начальное состояние воздуха в обоих случаях (при адиабатном и ири изотермическом сжатии) принять одинаковым.

163. Определить работу адиабатного расширения 0,7 нм³кислорода отt₁= 300° С доt₂= 0° С, считая зависимость теплоемкости от температуры криволинейной.

164. Определить давление и удельный объем в конце политропного расширения водорода, если показатель политропы n= 0,7. Начальные параметры:p₁= 6 ата иt₁= 10º С. Конечная температура равна 1000º С.

165. В результате политропного сжатия 0,2 нм³азота давление газа повышается от 1,2 ата до 18 ата. Чему равна работа сжатия? Как изменилась внутренняя энергия газа? Начальная температура 60° С. Показатель политропыn= 1,8.

166. В цилиндре двигателя внутреннего сгорания происходит сжатие воздуха до температуры, превышающей температуру самовоспламенения впрыскиваемого топлива. Какова должна быть степень сжатия, если температура воздуха в конце сжатия должна быть равной 500º С? Температура воздуха в начале сжатия равна 60° С. Сжатие происходит по политропе с показателем n= 1,3. Определить также работу, затрачиваемую на сжатие 1 кг газа.

167. В цилиндре происходит сжатие воздуха по политропе с показателем n= 1,25. Начальное давление воздуха равно 1,05 ата, начальная температура 10° С. До какого давления можно сжимать воздух, если его температура не должна превышать 170° С? Определить также, какую работу необходимо затратить на сжатие 1 ни воздуха в какое тепло должно быть при этом отведено от сжимаемого воздха.

168. Исследовать процесс политропного расширения воздуха при показателе политропы, равном: а) 0.6; 6) 1,1; в) 1,9:

У к а з а н и е. В результате исследования должны быть построены схемы трансформаци и энергии и установлено соотношение между изменением внутренней энергии, работой и теплом, участвующими в процессе.

169. Исследовать процесс политропного сжатия гелия при показателе политропы. равном: а) 0,9; 6) 1,3; в) 1,8 (см. указание к предыдущей задаче).

170. Определить количество тепла, участвующего в политропном процессе с 0,6 нм³кислорода, если в начальном состоянии р₁= 2 ата,t₁= 30° С. а в конечном состоянии р₂= 18 ата,t₂= 600° С. Определить также значение показателя политропы.

171. Построить график зависимости работы сжатия 1 нм³воздуха от показателя политропы сжатия в пределах: 1<n<k, если начальные параметры воздуха равны Р₁= 1 ата,t₁= 15° С, а конечное давление Р₂воздуха равно: а) 4 ата; б) 6 ата; в) 8 ата.

172. 1 кг кислорода совершает политропный процесс. Начальное давление газа 0,8 ата, начальный объем 4 м³конечное давление 3,1 ата, конечный объем 0,7 м³. Чему равна работа процесса? Каков объем газа при давлении 1 ата? Каково значение показателя политропы?

173. В результате некоторого волитропного процесса 1 кг воздуха совершил работу 12 810 кгм; при этом внутренняя энергия газа уменьшилась на 30 ккал. Во сколько раз уменьшилось давление воздуха? Начальная температура равна 250° С. Определить также показатель политропы.

174. В результате политропного процесса от 0,4 нм³окиси углерода отведено 12 ккал тепла. При этом температура газа повысилась от 0° до 300° С. Чему равен показатель политропы и как изменился объем газа в этом процессе?

175. На политропнос сжатие 2 кг азота затрачена работа 35 000 кгм. При этом внутренняя энергия газа возросла на 96 ккал. Как изменилось давление воздуха, если его начальная температура равна 30° С? Чему равен показатель политропы? Сколько тепла необходимо изохорно отвести от газа, чтобы температура стала равна начальной?

176. При политропном сжатии 1 кг азота его объем уменьшается в 6 раз. Работа сжатия равна 17 100 кгм/кг. Определить изменение давления в этом процессе. если начальная температура газа равна

17° С. Определить также показатель политропы.

1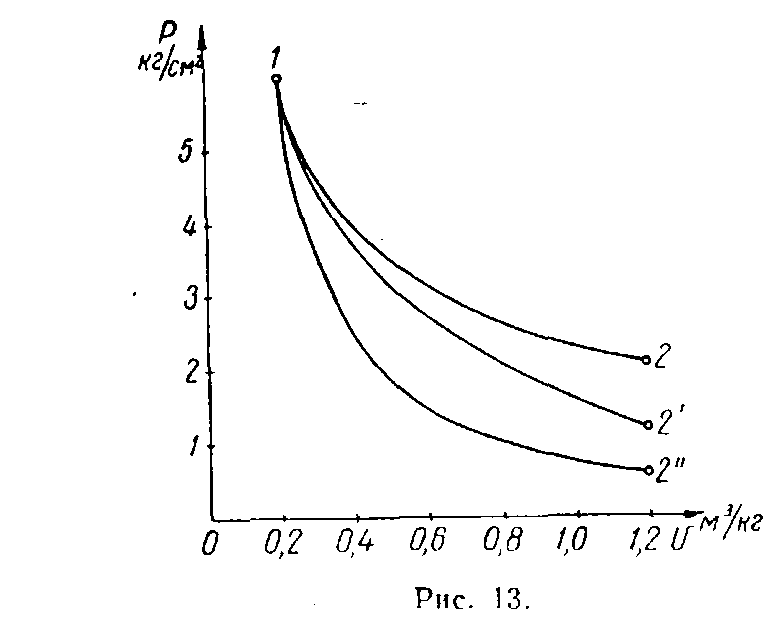77. 1 кг кислорода в результате подвода 30 ккал тепла совершает работу 6400 кгм. Во сколько раз увеличился объем газа? Как изменилась его энтальпия? Чему равен показатель политропы? Начальная температура газа равна 50С.

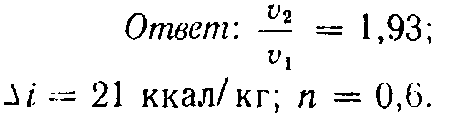
178. Путем построения графика процесса в логарифмических координатах проверить, являются ли политропными процессы изображенные на рис. 13.

179. Какое количество тепла необходимо отвести изохорно от

1 кг кислорода, находящегося в состоянии 1 (р = 4 ата, v₁= 1 м³/кг), чтобы последующим политропным сжатием при показателе политропыn= 0,9 его можно было привести в состояние 2 (p₂= 6 ата,v₂= 0,2 м³/кг)? Чему равна при этом работа сжатия?

Ответ: g= -152,5 ккал/кг:l= -20950 кгм/кг.

180. 1 нм³азота сжимается по политропе с показателемn= 1,2 так, что его объем уменьшается в 7 раз, а затем изотермически расширяется до первоначального объема. Определить работу и тепло, участвующие в процессе, а также конечное давление, если в начальном состоянииp₁₌ 1 ата,t₁= 60С.

Ответ: L=6150 кгм;Q=49,2 ккал; р₂=1,47 ата.

Энтропия. Смешение газов.

Энтропия.

Элементарное приращение энтропии рабочего тела в любом обратимом процессе определяется по формуле

Энтропия является функцией состояния. Поэтому ее изменение в каком-либо термодинамическом процессе может быть определено как разность значений энтропии в конечном и начальном состояниях процесса (или совокупности нескольких процессов). Применительно к идеальному газу и при условии, что теплоемкость постоянна, изменение энтропии может быть определено по одной из нижеследующих формул:

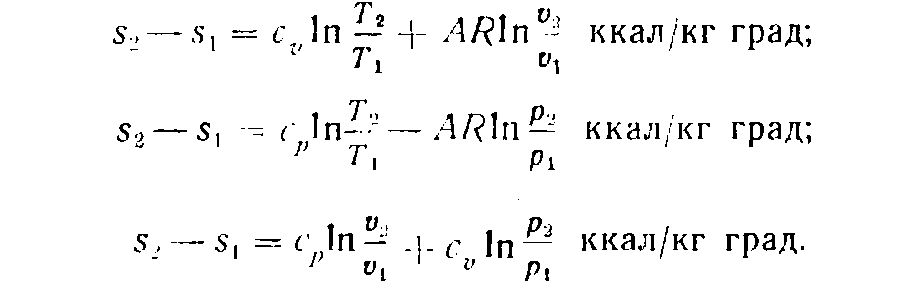
По приведенным формулам можно определить изменение энтропии самого рабочего тела и в необратимом процессе, если только конечное и начальное состояния являются равновесными. Если количество идеального газа равно Gкг, то изменение его энтропии определяется как

Иногда представляется удобным отсчитывать величину энтропии от некоторого ее значения, условно принятого в качестве нулевого. для газов принимают, что энтропия равна нулю при нормальных физических условиях. Значение энтропии идеального газа, отсчитанное от этого условного нуля, определяется по формулам

где v₀— значение удельного объема газа при нормальных физических условиях в нм³/кг. Для определения изменения энтропии идеального газа в результате совершения какого-либо политропного процесса удобно пользоваться формулой

где

с- истинная весовая теплоемкость газа (принимаемая постоянной) в данном процессе;

Т₁и Т₂, — начальная и конечная абсолютная температура газа, совершающего процесс.

Эта формула применима для всех политропных процессов, исключая изотермический процесс. Изменение энтропии идеального газа в изотермическом процессе может быть определено по формуле

Иногда при вычислении энтропии газа необходимо учесть зависимость теплоемкости от температуры. Примем линейную зависимость теплоемкости от температуры. Тогда

а истинная теплоемкость

Таким образом

Интегрируя от начального состояния до конечного, получим

Аналогично. используя’ зависимость

получим

и, наконец, из уравнения

получим

Вместо этих формул можно использовать предыдущие формулы, подставляя вместо истинной теплоемкости среднюю теплоемкость в заданном интервале температур, однако внося при этом известную условность и неточность. Средняя теплоемкость, формулы для определения которой были даны выше, получена путём усреднения по теплу

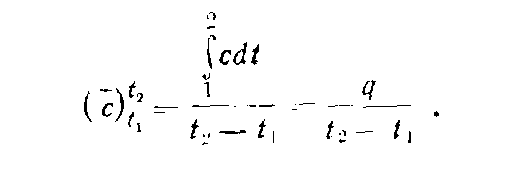
Приращение энтропии является логарифмической функцией температуры, а поэтому закон усреднения теплоемкости уже будет иным. Так, например, если зависимость истинной теплоемкости от температуры может быть представлена для двухатомных газов линейной зависимостью

то средняя теплоемкость, усредняемая по теплу g, будет иметь вид

а при усреднении в соответствии с формулой получим

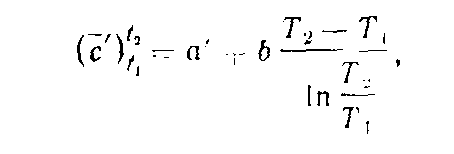
причем

можно доказать, что

где - поправочный коэффициент. Приимеем φ = 0,990; привеличина φ = 0,962; привеличина φ = 0,910.

Указанные цифры показывают, что при ошибка, вносимая в определение второго члена формулы дляне превышает 9%. Так как второй член линейной зависимости даже приt₁+t₂≈2000°С обычно не превышает 12% от значения самой теплоемкости, то ошибка, вносимая пренебрежением коэффициентом φ изменяет величину средней теплоемкости не более чем на 1—2%.

В случае необратимого процесса

Для адиабатного необратимого процесса, поскольку dq = 0 получим

ds>0

При рассмотрении изолированной системы, состоящей из нескольких тел, изменение энтропии системы равно сумме изменений энтропии отдельных тел, входящих в систему. Если внутри системы происходят только обратимые процессы, то для всей изолированной системы

Если в системе происходят необратимые процессы, то для системы в целом

т. е. энтропия изолированной системы возрастает.

Одним из типичных необратимых процессов является процесс смешения газов.

СМЕШЕНИЕ ГАЗОВ

Смещение газов полагают происходящим без теплообмена с окружающей средой. Различают два случая смещения газов: смещение при постоянном объеме и смещение при постоянном

давлении (смешение потоков).

В табл. 5 приведены формулы для определения объема, давления и температуры газов после смешения (для обоих случаев смешения).

Пример. Вычислить энтропию 1 кг азота при р= 3 ата и 300° С, приняв теплоемкость постоянной.

Решение.

Условно принимаем s= 0 при нормальных физических условиях.

По формуле

Пример. Вычислить энтропию 1 кг кислорода при давлении 5 ата и температуре 200° С, приняв линейную зависимость теплоемкости от температуры.

Решение.

Истинная весовая теплоемкость кислорода

Переходя к абсолютным температурам

Следовательно, a’_p= 0.2607;b= 0.0000508. Принимаяs₁= 0 при р₁= 1,033 ата и Т₁= 273º абс:

Пример. Определить изменение энтропии 2 кг азота в изохорном процессе, если p₁= 1 ата,t₁=27° С,p₂= 4 ата. Теплоемкость считать линейной функцией температуры.

Решение. Определяем конечную температуру в изохорном процессе:

Как и в предыдущей задаче, определяем коэффициенты иb. Пользуясь формулами

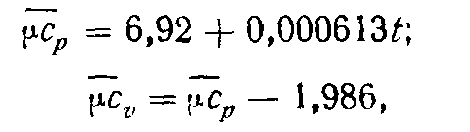
находим истинную изохорную теплоемкость

или

Следовательно

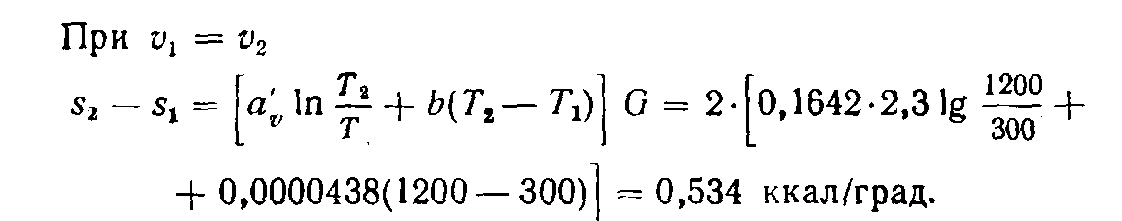
Решим эту же задачу, пользуясь средними теплоемкостями

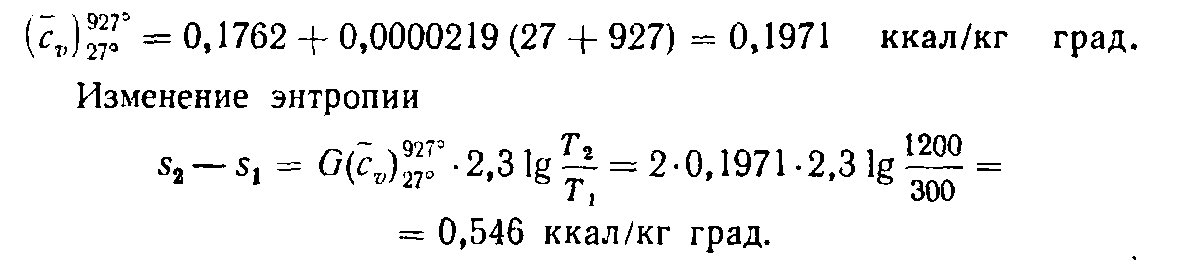
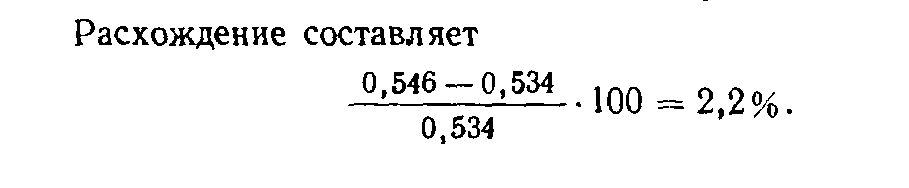
Пример. Начальное состояние воздуха определяется параметрами: p₁= 20 ата иt₁= 527º С. Воздух расширяется по политропе рv^1,2= соnstдо р₂= 1,2 ата, а затем приp₂=constсжимается до объемаv₃= 7v₁. Определить изменение энтропии за процесс 1 – 2 – 3 и представить процесс вTs—диаграмме, считая, что теплоемкость является величиной постоянной.

Решение. Вычисляем удельный объем воздуха в начале процесса

Затем определяем параметры воздуха в конце политропного расширения

Определяем температуру в конце процесса

Так как энтропия является функцией состояния, то ее изменение зависит только от значений параметров в начальном и конечном состояниях.

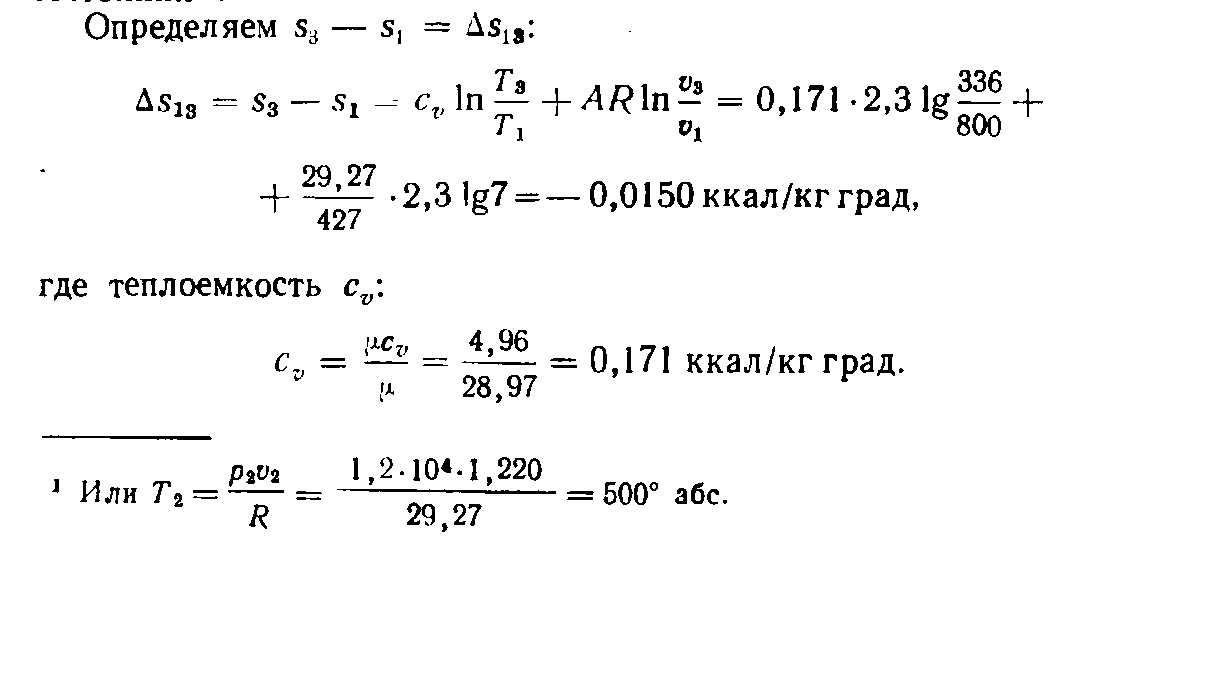
Для политропного процесса

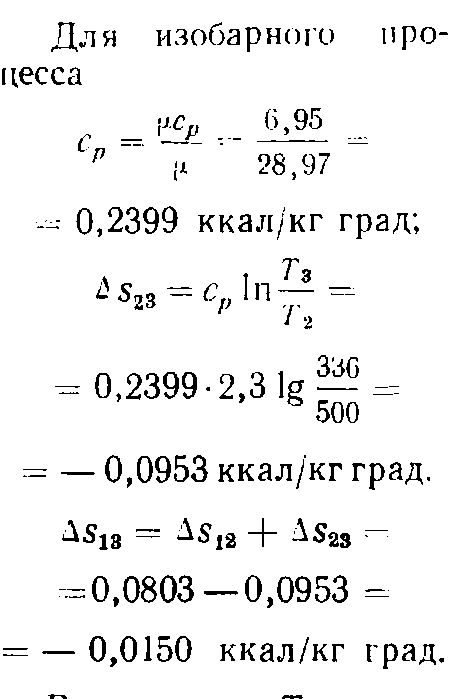
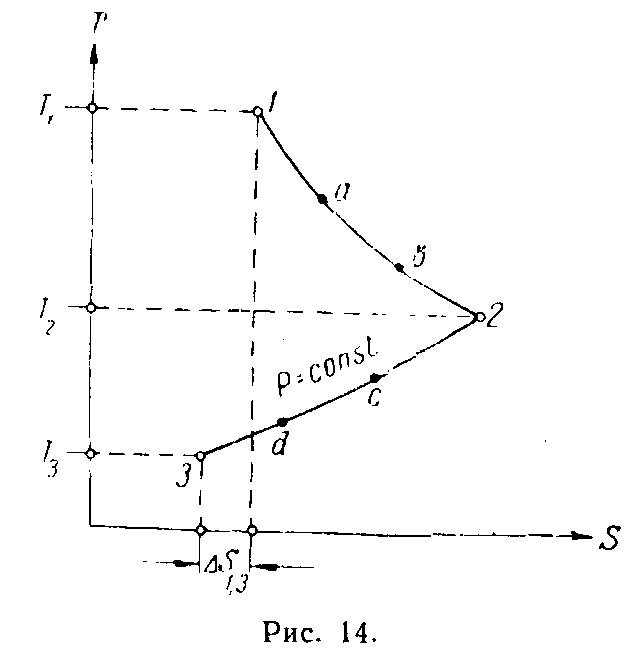
В диаграмме Тsпроцесс 1—2—3 можно построить, зная параметры в характерных точках 1, 2 и 3 и параметры промежуточных состояний (рис. 14).

Пример. 10 кг дымовых газов с начальной температурой 1300° С изобарно охлаждаются до 300° С, отдавая тепло воде при постоянной температуре кипения 200° С. Определить изменение энтропии Системы «дымовые газы — вода». Теплоемкость газов принять постоянной и равной 0,25 ккал/кг град.

Решение. В данном случае рассматривается система, состоящая из двух тел: 10 кг дымовых газов и вода. Оба тела, составляющие систему, считаются полностью изолированными от каких-либо воздействий со стороны внешней среды.

Изменение энтропии дымовых газов при постоянном давлении:

Количество тепла, полученное водой

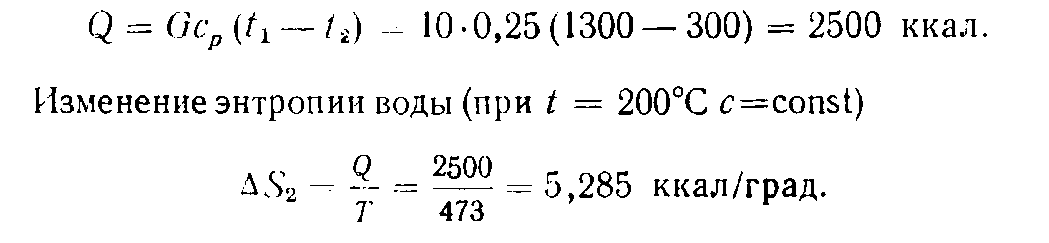
Изменение энтропии рассматриваемой системы

В итоге энтропия системы возросла на 2,763 ккал/град.

Пример. В сосуде емкостью 0,5 м³находится углекислый газ при температуре 100° С и давлении 2 ата. В другом сосуде емкостью 1,5 м³находится воздух при температуре 250° С. Какое давление необходимо создать в сосуде с воздухом, чтобы при соединении сосудов друг с другом получить 8 кг смеси? Определить давление и температуру после смешения. Определить внутреннюю энергию газовой смеси, условно считая, что при 0° С значение внутренней энергии газа равно нулю.

Решение. Весовое количество углекислого газа до смешения

Весовое количество воздуха до смешения

Давление в сосуде с воздухом до смешения

Смещение газов происходит при постоянном объеме. Температуру смеси можно определить по формуле

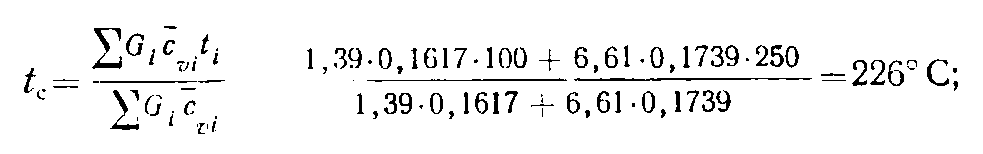
теплоемкости с_vберутся из таблиц.

Давление после смешения находим по формуле

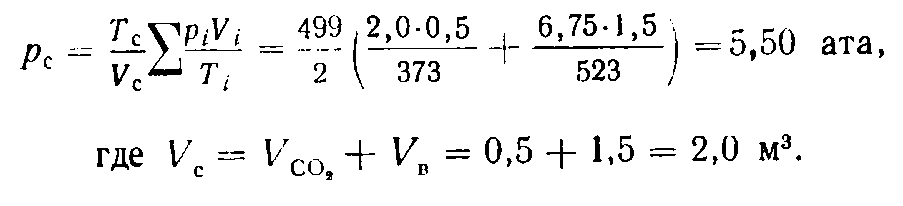
Внутреннюю энергию после смещения получаем из выражения

Пример. Баллон, содержащий 2 кг воздуха при давлении 2 ата и температуре 100° С, сообщается с другим баллоном такого же объема, содержащим воздух при давлении 10 ата и температуре 150° С. Какое давление и температура установятся после сообщения сосудов? Каково изменение энтропии в результате смещения обоих количеств воздуха?

Решение. Объем баллонов

Количество воздуха во втором баллоне

Общий объем после смещения

Температура воздуха после смешения может быть определена по упрощенной формуле, так как смешению подвергаются двухатомные газы, температуры которых отличаются всего на 50° С, в связи с чем зависимостью теплоемкости от температуры можно пренебречь

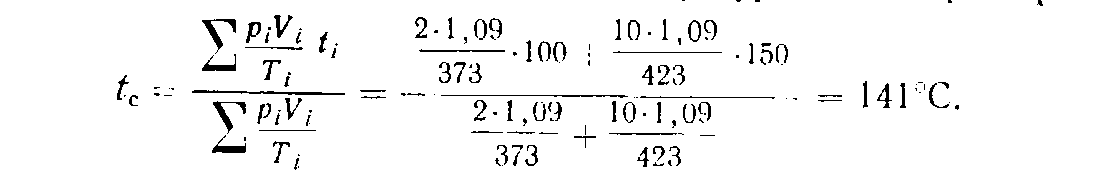
Давление воздуха после смешения

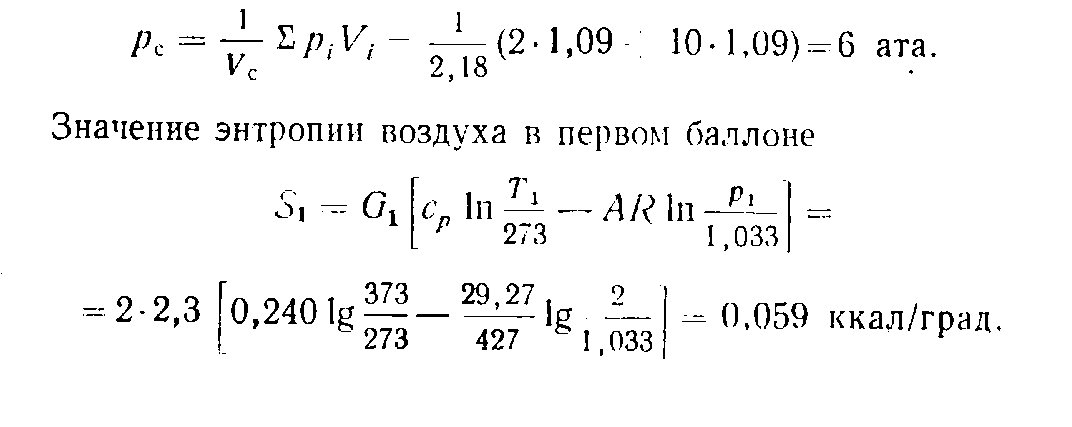
Значение энтропии воздуха во втором баллоне

Энтропии воздуха после смешения

Изменение энтропии системы

Пример. По двум газопроводам к месту смешения подается кислород и азот. Часовой расход кислорода 250 кг/час, давление4 ата, температура 500° С, а часовой расход азота 100 кг/час, давление 2 ата и температура 300° С.Давление после смешения 1,8 ата. Определить температуру и объемный расход смеси в общем газопроводе, а также изменение энтропии при смешении обоих потоков.

Решение. Смещение происходит при постоянном давлении. Определяем температуру после смешения потоков по формуле (см. табл. 5)

Объемный расход смеси определим по формуле

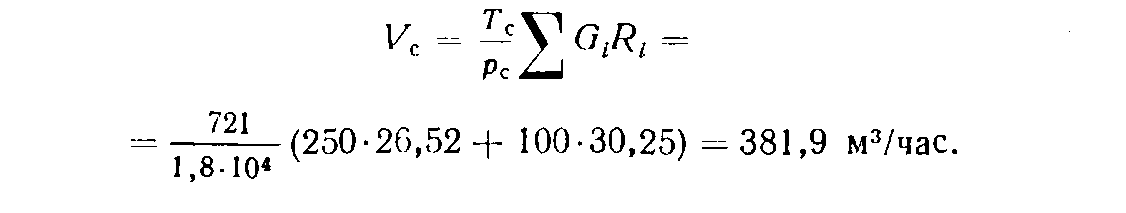
Определим весовые доли кислорода O₂и азотаN₂в смеси

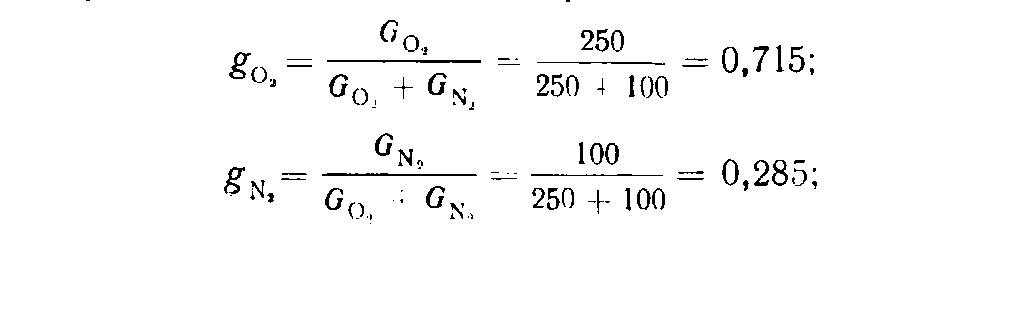
а затем газовую постоянную смеси

Изменение энтропии при смещении потоков определяем при условии линейной зависимости теплоемкости от температуры. Для кислорода и азота имеем:

Соответственно истинные весовые теплоемкости

Переходя к абсолютным температурам, получаем:

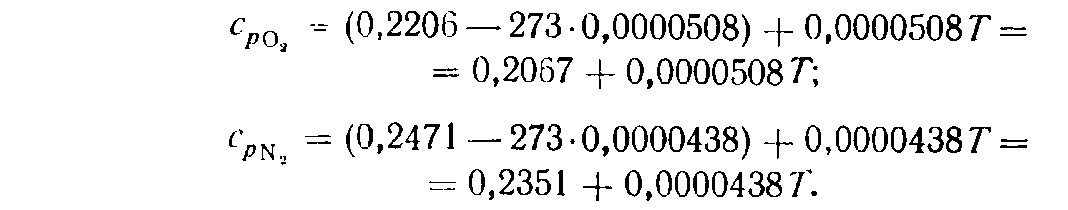
Значение удельной энтропии кислорода и азота в соответствующих газопроводах определяется по формуле

Пользуясь этой формулой, получаем

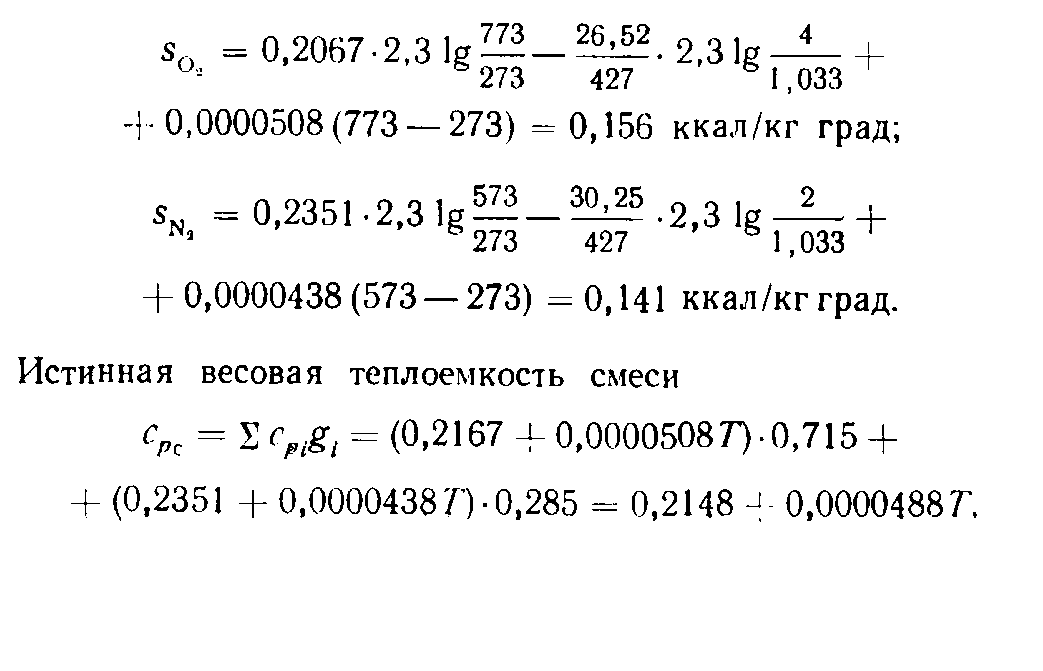
Следовательно, для смеси газов имеем: = 0,2148; Ь_с= 0,0000488.

Тогда значение удельной энтропии после смещения

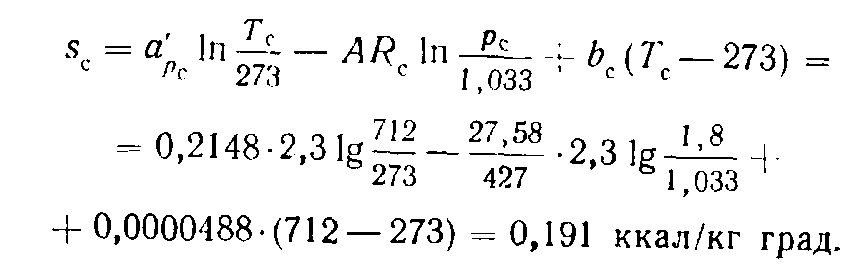
Приращение удельной энтропии в процессе смешения

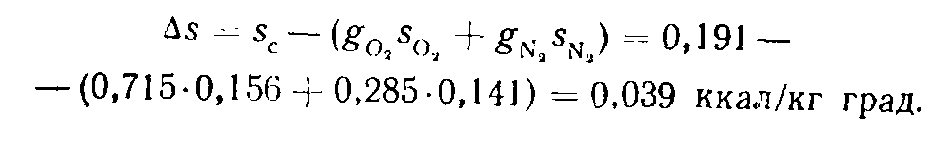
Задачи

181. Воздух находится при нормальных физических условиях. Как изменится энтропия 12 кг воздуха, если в изохорном процессе температура его поднялась до 850° С?

Ответ: S= 2,899 ккал/град.

182. Определить энтропию 1 кг воздуха при давлении 3 ата и температуре 420° С в случае постоянной теплоемкости с_р= 0,240 ккал/кг град = соnstи переменной теплоемкости с_р= 0,2399 + 0,0000398tккал/кг град.

Ответ: При постоянной теплоемкости s= 0,124 ккал/кг град;

при переменной теплоемкости s= 0,130 град.

183. 2 м³воздуха с начальной температурой 17° С получают извне 200 ккал тепла, вследствие чего объем воздуха увеличивается до 3,2 м³. Подвод тепла осуществляется изобарно. Определить конечную температуру и изменение энтропии воздуха. Теплоемкость с считать постоянной и равной 0,240 ккал/кг град.

Ответ: t₃= 191° С;S= 0,540 ккал/кг град.

184. 1 кг воздуха, имеющий начальную температуру 15° С, изобарно расширяется при давлении 2 ата до двойного объема, а затем изохорно нагревается до давления 3 ата. Определить работу процесса и изменение энтропии газа, если теплоемкость с_р= 0,240 ккал/кг град. Представить процесс в рvи Т диаграммах.

Ответ: l= 8430 кгм;S= 0,2173 ккал/кг град.

185. При изотермическом сжатии азота в количестве 2,1 м³отводится 80 ккал тепла. Начальное давление 1 ата. Определить изменение энтропии газа в процессе сжатия.

Ответ: S= —0,115 ккал/кг град.

186. Воздух, взятый при нормальных физических условиях, сжимается при постоянной энтропии до 3 ата, а затем охлаждается в изобарном процессе до 0° С. Определить изменение энтропии, если в конце процесса объем воздуха равен 1 м³. Представить процесс в рvи Т диаграммах.

Ответ: S= —0,2742 ккал/град.

187. 4 кг окиси углерода политропно сжимаются, вследствие чего температура изменяется от 100° до 50° С. Показатель политропы n= 0,7. Определить изменение энтропии, если с_р= 0,177 ккал/кг град иk= 1,4.

Ответ: S= —0,237 ккал/кг град.

188. 3 кг воздуха расширяются по политропе рv= соnst. Начальная температура 127° С. Определить изменение энтропии, если работа расширения составляет 4270 кгм, а теплоемкость с_р= 0,171 ккал/кг град.

Ответ: S= 0,00637 ккал/град.

189. Для 1 кг кислорода построить в диаграмме Тsлинии изохорv₁= 0,3 м³/кг;v₂= 0,6 м³/кг;v₃= 0,9 м³/кг и линии изобарp₁= 2 ата; р₂= 4 ата; р₃= б ата. При построении принять теплоемкость постоянной.

190. К 10 кг углекислого газа, начальные параметры которого Р₁= 1 ата иt₁= 60° С, изохорно подводится тепло, в результате чего давление газа повышается до 2 ата. Затем газ изотермически расширяется до начального давления р₃= р₁= 1 ата. Определить изменение энтропии в процессе 1—3. Представить процесс в рvи Тsдиаграммах. Принять теплоемкость зависящей от температуры.

Ответ: S= 2,855 ккал/град.

191. При политропном расширении воздуха давление уменьшается от 4 ата до 1 ата, а удельный объем увеличивается от 0,23 м³/кг до 0,86 м³/кг. Определить изменение энтропии в процессе. Теплоемкость считать постоянной.

Ответ: S= 0,0806 ккал/кг град.

192. В топке парового котла поддерживается постоянная температура 1500° С. Тепло в количестве 2000 ккал с каждого сгоревшего кг топлива посредством лучеиспускания передается поверхностям нагрева котла, имеющим постоянную температуру 2500° С. Определить изменение энтропии рассматриваемой системы.

Ответ: S= 2,70 ккал/ град на 1 кг сгоревшего топлива,

193. В баллоне емкостью 80 л находится сжатый кислород при давлении 25 ата и температуре 22° С. Вследствие плохой посадки запирающего клапана происходит постепенный выпуск кислорода в атмосферу, имеющую давление 1 ата и температуру 22°С. Определить изменение энтропии системы "кислород баллона и окружающий воздух", предполагая, что температура выпускаемого кислорода не изменяется.

Ответ: S= 0,358 ккал/град.

194. Определить изменение энтропии изолированной системы из двух однородных тел (с = 0,1 ккал/кг град) в процессе выравнивания их температуры. Вес первого тела 5 кг, температура 20° С; вес второго тела 2 кг, температура 1000° С.

Ответ: S= 0,176 ккал/ град.

195. В теплоизолированном сосуде происходит смешение 2 кг воды при температуре 10°С и 3 кг воды при температуре 90° С. Определить возрастание энтропии в результате процесса смешения, считая, что при 0° С энтропии воды условно принята равной нулю. Теплоемкость воды принять равной 1 ккал/кг град.

Ответ: S= 0,033 ккал/град.

196. В результате некоторого политропного процесса, проведенного с 3,5 кг азота, температура газа возросла от 30° до 600° С. При этом энтропия газа уменьшилась на 1,5 ккал/ град. Определить показатель политропы и указать, сжимается или расширяется газ. Теплоемкость считать постоянной.

Ответ: n= 1,12; происходит сжатие газа.

197. Из резервуара емкостью 10 м³воздух давления 2 ата и температуры 27° С вытекает в другой резервуар емкостью 5 м³. Определить температуру, давление и изменение энтропии после полного выравнивания давления в обоих резервуарах, если во втором резервуаре до перепуска воздуха была пустота и оба резервуара тщательно изолированы от окружающей среды. Теплоемкость с_р= 0,240 ккал/кг град и с_v= 0,171 ккал/кг град.

Ответ: V =15 м³; р = 1,33 ата;

t=27° С;S=0,028 ккал/кг град.

198. В двух баллонах емкостью 25 л и 55 л находятся соответственно кислород и воздух при нормальных физических условиях. Какое давление должно быть в сосуде с кислородом, чтобы при соединении его с сосудом, наполненным воздухом, получить давление смеси, равное 5 ата?

Ответ: Р(О₂) = 13,7 ата.

199. Трубопровод, соединяющий два сосуда, перекрыт клапаном. В первом сосуде, емкостью 75 л. находится сжатый воздух при давлении 60 ата и температуре 250° С; второй сосуд, емкостью 60 л, заполнен воздухом при температуре 15° С (показание барометра 760 мм рт. ст.). Какое давление и температура ‚становятся после сообщения сосудов? Определить значение внутренней энергии воздуха после смешения, принимая, что при 0°С внутренняя энергия газа условно равна нулю.

Ответ: t_c= 245° С; р_c= 33,8 ата;U= 127 ккал

200. В первом сосуде емкостью 20 л находится кислород под давлением 5 ата при температуре 200° С; во втором сосуде емкостью 30 л находится азот под давлением 8 ата при температуре 250° С и в третьем сосуде емкостью 5 л находится углекислый газ под давлением 2 ата при температуре 150° С. Определить давление и температуру, которые установятся во всех трех сосудах после их соединения между собой. Теплоемкость определять по таблицам.

Ответ: р_с= 6,35 ата;t_c= 230° С.

201. В сосуде емкостью 0,2 м³находится 7 кг азота при температуре 150° С; в другом сосуде емкостью 0,1 м³находится 1,5 кг углекислого газа при температуре 90° С. Какое давление и температура установятся, если соединить сосуды друг с другом, в каково будет приращение энтропии в результате процесса смещения? Чему равны парциальные давления компонентов в смеси? Теплоемкость принять постоянной.

Ответ: t_c= 138°C; Р_с= 32,8 ата; P(N₂) = 28,9ата;

P(CO₂) = 3,9 aта; S = 0,063 ккал/град.

202. Два вентилятора производительностью 1000 нм³/час и 1600 нм³/ч подают воздух в общий воздуховод. Воздух, нагнетаемый первым вентилятором, имеет температуру 120°С, вторым 30°С. давление воздуха до смещения и после смещения одинаково и равно 1,06 ата. Определить температуру и объемный расход воздуха в общем воздуховоде, а также изменение энтропии в процессе смешения. Теплоемкость принять постоянной.

Ответ: t_c= 64° С;V_c= 3130 м³/ч

S= 0,0016 ккал/град

203. Поток азота, имеющий часовой расход 350 м³/ч давление 2 ата и температуру 50° С, смешивается с потоком воздуха, имеющим часовой расход 500 м³/ч, давление 1,5 ата и температуру 600°С. давление смеси в общем трубопроводе 1,5 ата. Определить состояние смеси в общем трубопроводе и изменение энтропии в результате процесса смешения.

Ответ: t_c= 211° С;V_c= 945 м³/ч;S= 0,044 ккал/кг град.

204. В котельных установках иногда для подогрева воздуха. поступающего в топку котла, производят его смешение с отходящими дымовыми газами. Объемный состав дымовых газов: СО₂= 15%; О₂= 4%; СО = 1,5%;N₂= 79,5%. Температура отходящих газов 300° С, температура поступающего воздуха 30° С. Определить температуру газо-воздушной смеси и процентное содержание кислорода в смеси, если весовое соотношение между дымовыми газами и воздухом равно 0,25. давление дымовых газов и воздуха до и после смешения одинаково и равно 1,05 ата.

Ответ: t_c= 85° С; О₂= 17,7%.

205. Дымовые газы от трех котлов удаляются через общую дымовую трубу. Объемный состав дымовых газов после каждого котла принять одинаковым и равным: СО₂= 12%; О₂= 6,5%; СО = 3,5%;N₂= 78%. Количество газа, удаляемое от каждого котла, соответственно составляет 1500 м³/ч при температуре 220° С, 2500 м³/ч при температуре 270° С и 6000 м³/ч при температуре 330° С. Давление в газоходах всех трех котлов одинаковое. Определить температуру после смешения и объемный расход газов через дымовую трубу.

Ответ: t_c= 295° С;V_с= 10000 м³/ч

206. В двух баллонах содержится по 1 кг воздуха. Определить изменение энтропии воздуха при соединении баллонов между собой, если: а) давление в баллонах одинаково и равно 2 ата, а температура в одном 17°, а в другом 127° С; 6) температуры в баллонах одинаковы и равны 17° С, а давление в одном 1,2 ата, а в другом 3 ата.

Ответ: а) S= 0,0055 ккал/град; б)S= 0,0142 ккал/град.

207. 1 моль воздуха при давлении 4 ата и температуре 100° С смешивается с 1 молем углекислого газа при давлении 2 ата и температуре 50° С. Определить давление и температуру смеси и изменение энтропии в результате процесса смешения. Теплоемкость принять постоянной.

Ответ: р_с= 2,7 ата;t_c= 73°С;S= 0,195 ккал/град.

208. Определить температуру смеси после смещения 6 м³дымовых газов (R= 29,7 кгм/кг град) при температуре 600° С и 2 м³воздуха при температуре 17° С. давление воздуха и дымовых газов 743 мм рт. ст. Найти также объем смеси и изменение энтропии в результате процесса смешения. Теплоемкость дымовых газов принять равной теплоемкости воздуха и считать ее постоянной.

Ответ: t_c= 307° С;V_c= 8,0 м³;S= 0,166 ккал/град.

РАЗДЕЛ ВОСЬМОЙ

КРУГОВЫЕ ПРОЦЕССЫ. ЦИКЛ КАРНО

Круговым процессом или циклом называется совокупность термодинамических процессов, в результате осуществлении которых рабочее тело возвращается в исходное состояние.

Круговой процесс в координатах рvили Тsизображается замкнутым контуром. Площадь, заключенная внутри этого контура, изображает работу (в соответствующих единицах), совершаемую рабочим телом за цикл.

П р я м о й цикл осуществляется по часовой стрелке и является прототипом для всех тепловых двигателей. О б р а т н ы й осуществляется против часовой стрелки и является прототипом для всех холодильных установок.

Работа l, получаемая за цикл от 1 кг рабочего тела, определяется по формуле

где q₁ккал/кг — количество тепла, подведенное к рабочему телу от теплоотдатчиков, и |q₂| ккал/кг — абсолютное количество тепла. отведенное от рабочего тела к теплоприемникам.

Т е р м и ч е с к и й к. п. д. ц и к л а определяется по формуле

Обратный цикл характеризуется отношением

называемым холодильным коэффициентом.

В заданном температурном интервале максимально возможным термическим к. п. д. обладает ц и к л К а р н о.

Термический к. п. д. цикла Карно равен

где Т₁и Т₂— абсолютные температуры соответственно теплоотдатчика и теплоприемника.

Количество подведенного тепла в цикле Карно

количество отведенного тепла

Если цикл является необратимым (вследствие необратимого протекания одного или нескольких процессов, составляющих цикл), работа цикла уменьшается по сравнению с работой обратимого ЦИКЛА на величину

где ∆S_сист— возрастание энтропии системы¹вследствие необратимости одного или нескольких процессов в ккал/град;

Т₂— температура теплоприемника в °абс.

Величину ∆Lпринято называть потерей работоспособности цикла.

Термический к. п. д. необратимого цикла равен

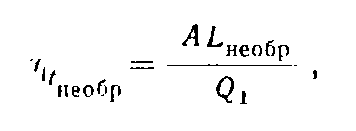
гдеL_необр=L_обр– ∆L– работа необратимого цикла в кгм;

L_обр— работа обратимого цикла, совершающегося между теми же теплоотдатчиками

и теплоприемниками (и при том же количестве подведенного тепла) в кгм;

Q₁— количество подведенного тепла в ккал.

Пример. Определить параметры рабочего тела в характерных точках цикла Карно, а также количество подведенного и отведенного тепла, работу и термический к. п. д. цикла, если известно, что максимальная и минимальная температуры цикла равны соответственно 600° и 100° С, а максимальное и минимальное давления его — 60 ата и 1 ата. Рабочим телом является воздух.

Р е ш е н и е. Характерными точками цикла называют ТОЧКИ пересечения кривых различных процессов. В данном случае такими точками являются точки 1, 2, 3 и 4 (рис. 15 и 16). Заданными являются следующие величины; Р₁= 60 ата; р₃= 1 ата;t₁=t₂= 600° С;t₃=t₄= 100° С. Определим остальные значения параметров рабочего тела в характерных точках цикла.

Точка 1. Из уравнения состояния находим

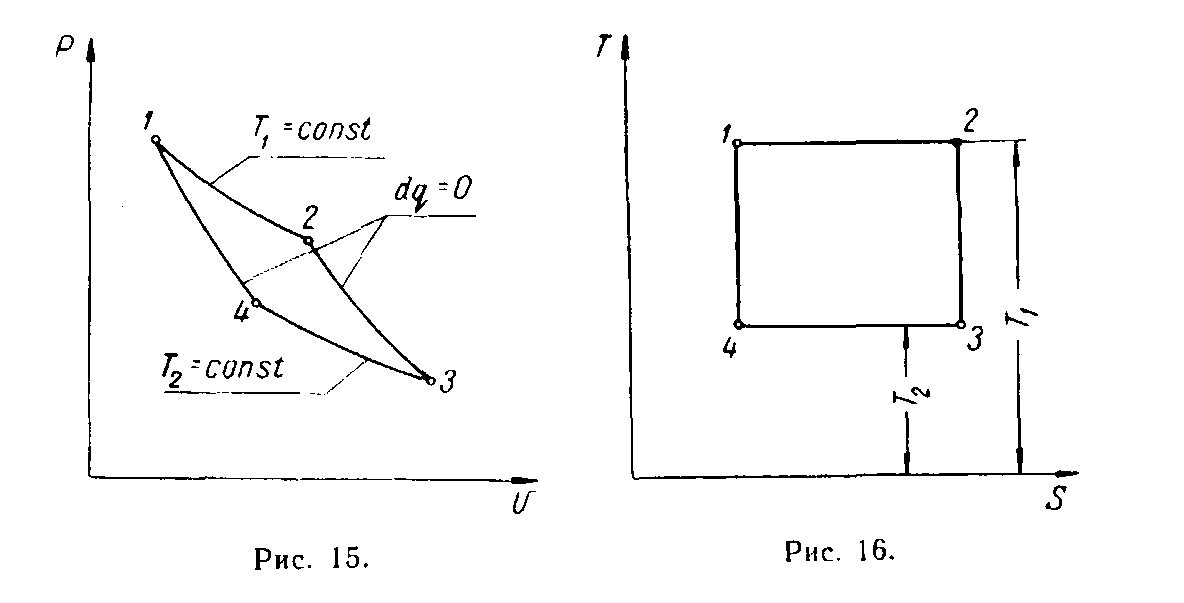
Точка 2. Из соотношения параметров в адиабатном процессе 2—3 получаем

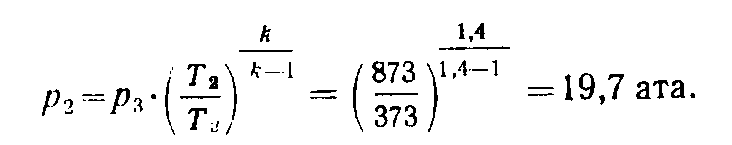
Из уравнения изотермы 1—2 находим

Точка 3. Из уравнения состояния находим

Точка 4. Из соотношения параметров в адиабатном процессе 4—1 получаем

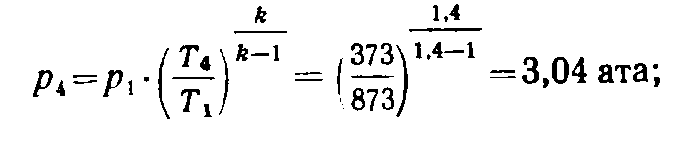
а из уравнения изотермы 3—4

Запишем параметры рабочего тела в характерных точках цикла в таблицу:

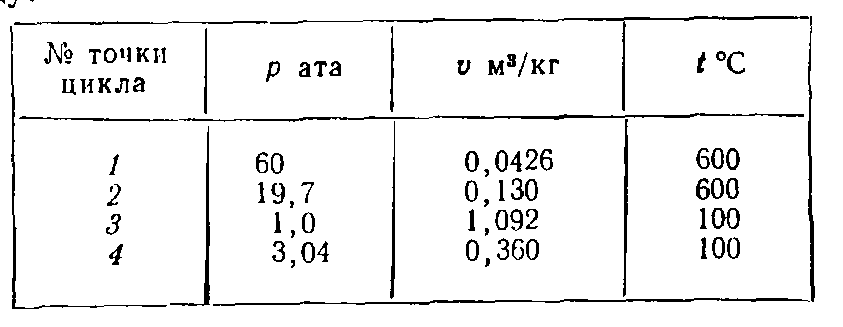
Количество подведенного тепла

Количество отведенного тепла

Работа, полученная за цикл

Термический к. п. д. цикла

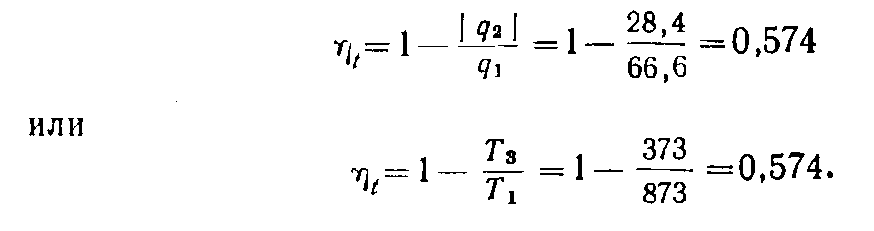
Пример. Определить термический к. п. д. цикла Карно, в котором при адиабатном сжатии давление рабочего тела повышается в 12 раз. Рабочее тело — двухатомный газ.

Р е ш е н и е. Для определения термического к. п. д. цикла Карно достаточно знать отношение абсолютных температур теплоотдатчика и теплоприемника. Это отношение можно найти по заданному повышению давления при адиабатном сжатии

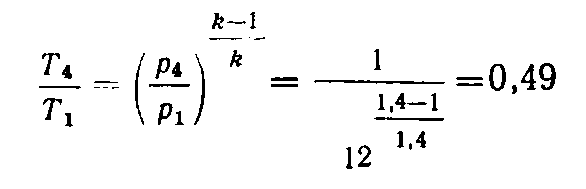
(индексы у величин Т и р приняты в соответствии с нумерацией характерных точек цикла на рис. 15).

Следовательно, термический к. п. д. цикла равен

Пример. Определить термический к. п. д. и работу цикла Карно, в котором давление рабочего тела в начале адиабатного расширения и адиабатного сжатия одинаково. В цикле подводится 80 ккал/кг тепла 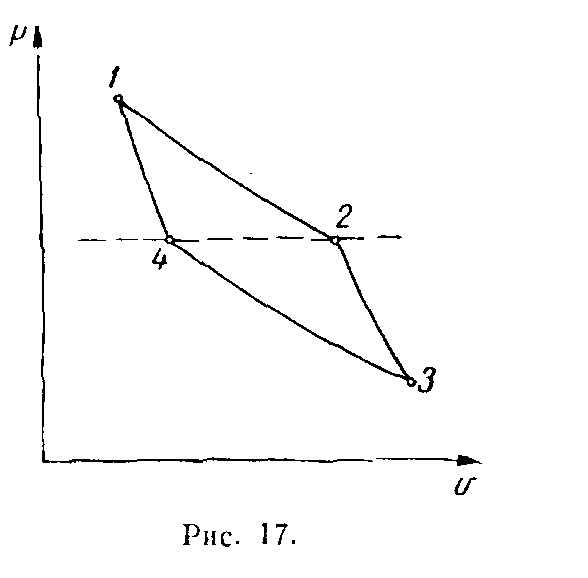при температуре 700° С. Рабочее тело обладает свойствами кислорода.

Р е ш е н и е. Изобразим цикл в координатах рv(рис. 17).

Из формулы для подведенного тепла находим отношение давлений в начале и в конце изотермического расширения

Но по условиям задачи . По отношению давлений находим отношение абсолютных температур в начале и в конце адиабатного сжатия

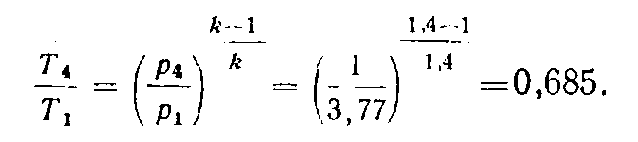
Термический к. п. д. цикла Карно

Работа, получаемая за цикл

Пример. Определить работу и термический к. п. д. обобщенного цикла Карно, состоящего из двух изотерм и двух изобар, если известно, что энтропия рабочего тела уменьшается при изобарном сжатии на 0,095 ккал/кг град, а при изотермическом сжатии — на 0,125 ккал/кг град. Температура теплоотдатчика равна 127°С. Рабочее тело окись углерода.

Р е ш е н и е. Изобразим цикл в диаграмме Тs(рис. 18). Так как изобары 4—1 и 2—3 являются эквидистантными кривыми, то заштрихованные площади 4—1—1’ и 3—2—2’ равны, а следовательно пл. 1—2—3—4 = пл. 1—2—2’—1’ Это означает, что работа рассматриваемого цикла может быть вычислена как

В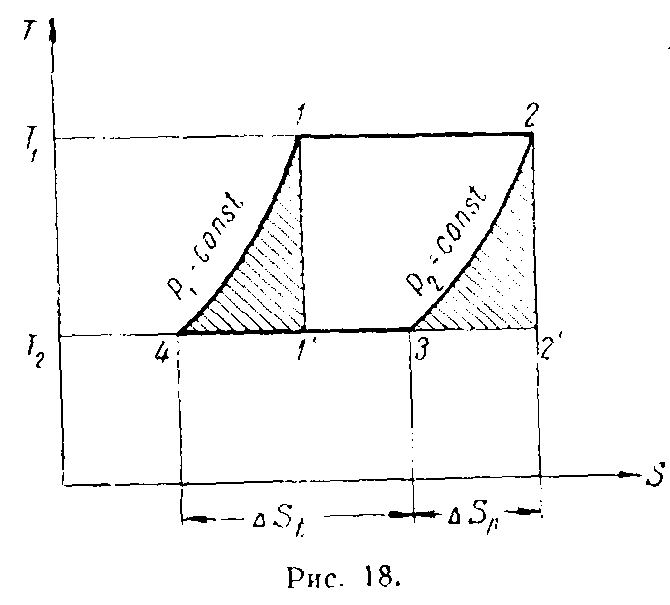следствие эквидистантности изобар 4—1 и 2—3 имеем

Поэтому

Для вычисления температуры Т₂воспользуемся формулой изменения энтропии, применяя ее к изобарному процессу 2—3. Из этой формулы следует:

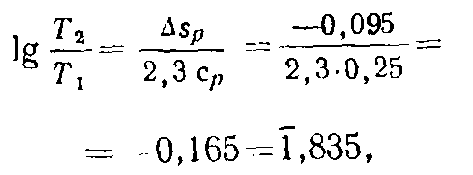
где - изобарная теплоемкость окиси углерода.

Таким образом

в искомая температура

Следовательно

Термический к. п. д. рассматриваемого цикла

Пример. Определить термический к. п. д. цикла, который состоит из адиабаты сжатия 1—2, изотермы расширения 2—3 и изохоры 3—1. Степень сжатия равна 3,5. Рабочее тело — кислород. Изобразить цикл в координатах рvи Тs. Определить также термический к. п.д. цикла Карно, совершающегося в том же температурном интервале.

Р е ш е н и е. Изображение цикла в координатах рvи Тsпри ведено на рис. 19 и 20. Подвод тепла в этом цикле происходит по изотерме 2—3, а отвод тепла — по изохоре 3—1.

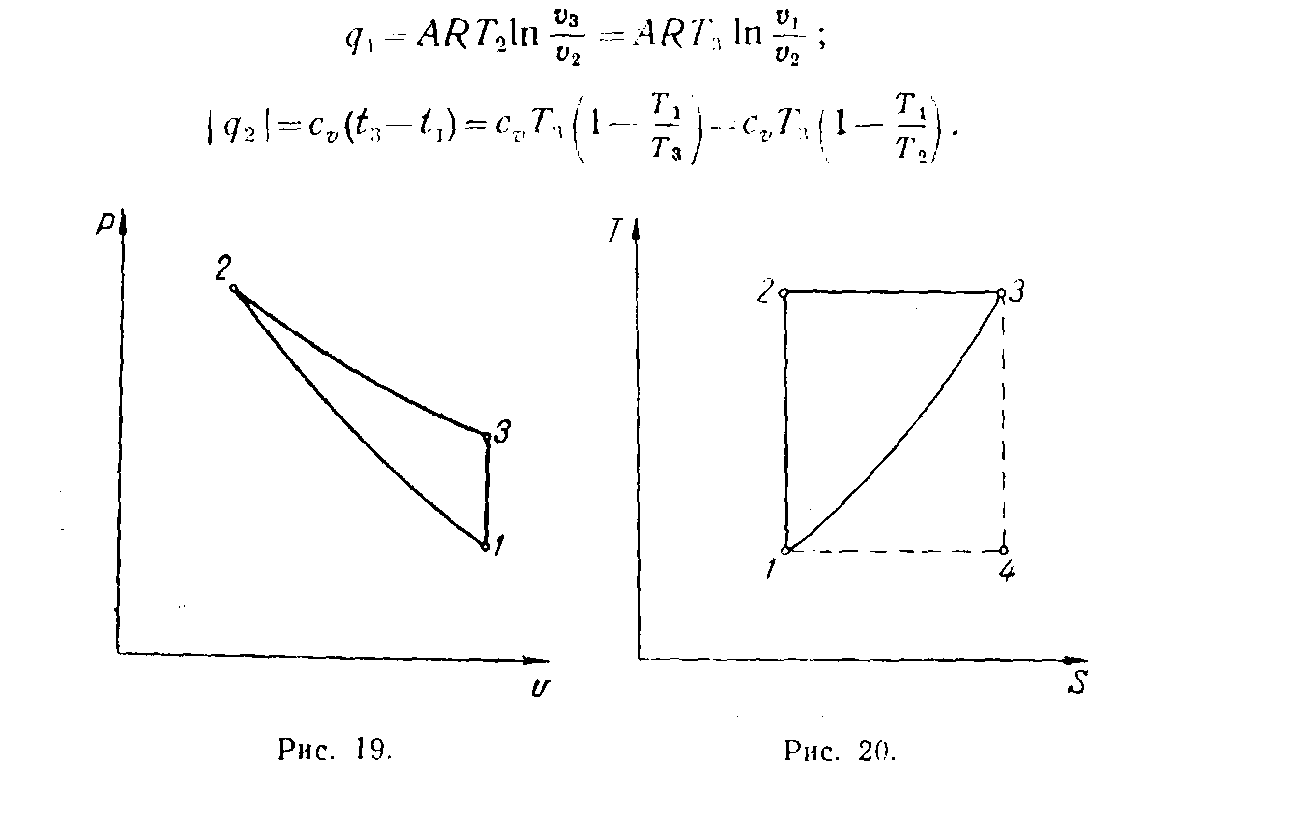
Термический к. п. д. рассматриваемого цикла

Отношение абсолютных температур определяется из соотношения между параметрами в адиабатном процессе

Подставляя это значение в выражение термического к. п. д., а также имея в виду, что АR= с_p— с_vи— степень сжатия, получаем следующую формулу для вычисления термического к. п. д. цикла

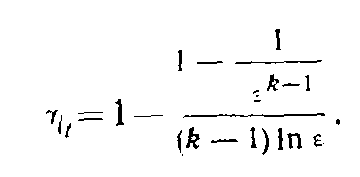
Следовательно, термический к. п. д. рассматриваемого цикла зависит только от степени сжатия и от свойств рабочего тела (показателя адиабаты). От начального состояния рабочего тела термический к. п. д. цикла не зависит.

Для кислорода k= 1.4. При ε = 3,5 по этой формуле получаем:

Определим термический к. п. д. цикла Карно. совершающегося в том же температурном интервале. Цикл Карно изображается фигурой 1—2—3—4 (рис. 18). Температурный интервал ограничен максимальной и минимальной температурами заданного цикла. Поэтому к. п. д. цикла Карно

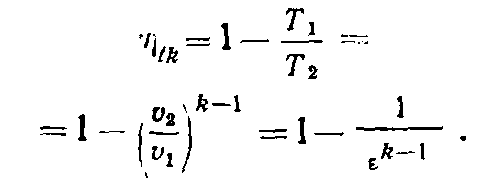
Подставляя сюда k= 1.4 и ε = 3,5, получаем

Пример. Цикл состоит из адиабаты сжатия 1—2, политропы расширения 2—3 и изохоры 3—1. Определить термический к. п. д. и работу цикла, если температура в начале сжатия равна 0° С, температура в конце расширения равна 400° С, а степень сжатия равна 5,5. Рабочее тело - воздух. Теплоемкость считать постоянной. Изобразить цикл в координатах рvи Тs

Р е ш е н и е. Изображение цикла в координатах рvприведено на рис. 21. Взаимное расположение точек 1 и 3 на этом графике определяется заданными значениями температур. Если бы температура в конце расширения была ниже, чем температура в начале сжатия, то точка 3 располагалась бы ниже точки 1.

В координатах Тsцикл можно будет изобразить после того как будет найден показатель политропы 2—3.

Температура в точке 2 (из уравнения адиабаты 1—2)

Уравнение политропы 2—3

Отсюда показатель политропы 2—3:

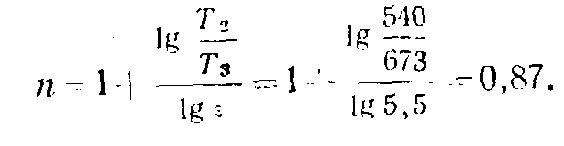
После того как определено, что процесс расширения является политропой 1-й группы (0<n<1), можно изобразить цикл в координатах Тs(рис. 22).

Подвод тепла в заданном цикле происходит по политропе 2—3, отвод тепла — по изохоре 3—1. Количество подведенного тепла равно

Количество отведенного тепла

Работа, полученная за цикл

Термический к. п. д. цикла

Пример. Между теплоотдатчиком (t₁= 6000° С) и теплоприемником (t₂= 40° С) совершается обратимый цикл Карно, работа которого равна 8000 кгм. Как изменится термический к. п. д. цикла, если при тех же температурах теплоотдатчика и теплоприемника и при том же количестве подведенного тепла рабочее тело при изотермическом подводе тепла будет иметь температуру 5000° С? Определить также потерю работоспособности цикла.

Р е ш е н и е. В обратимом цикле Карно температура рабочего тела в процессе изотермического подвода тепла (расширения) равна температуре теплоотдатчика, а в процессе изотермического отвода тепла (сжатия) она равна температуре теплоприемника. Термический к. п. д. обратного цикла Карно:

Количество подведенного тепла

Во втором случае имеет место необратимый цикл Карно. Необратимым является процесс подвода тепла к рабочему телу, так как он протекает при конечной (а не бесконечно малой) разности температур теплоотдатчика и рабочего тела. В результате необратимости этого процесса имеет место возрастание энтропии системы

Здесь ∆S₁— изменение энтропии теплоотдатчика: оно определяется делением теплаQ₁= 29,2 ккал на абсолютную температуру теплоотдатчика и имеет знак минус, так как тепло отводится от теплоотдатчика:

∆S_р-τ— изменение энтропии рабочего тела в процессе изотермического подвода тепла; оно определяется делением теплаQ₁ = 29,2 ккал на абсолютную температуру рабочего тела в этом процессе и имеет знак плюс, так как тепло подводится к рабочему телу;

Остальные процессы цикла остаются обратимыми и не вызывают возрастания энтропии системы.

Таким образом

и, следовательно, потеря работоспособности цикла равна

Термический к. п. д. необратимого цикла Карно

Следовательно, термический к. п. д. цикла уменьшился на

или на

Термический к. п. д. необратимого цикла Карно можно определить и иначе. Представим себе, что между теплоотдатчиком и рабочим телом находится некоторый передатчик тепла, температура которого равна температуре рабочего тела в процессе изотермического подвода тепла (500° С). Этот воображаемый теплопередатчик воспринимает тепло Q₁от теплоотдатчика в отдает его рабочему телу. Теперь изотермический процесс подвода тепла к рабочему телу является обратимым, так как температура рабочего тела и промежуточного теплопередатчика одинакова (точнее, отличается на бесконечно малую величину). Необратимым в системе является процесс передачи теплаQ₁от теплоотдатчика к промежуточному теплопередатчику.

Таким образом, при наличии промежуточного передатчика тепла рассматриваемый необратимый цикл Карно можно считать обратимым и его термический к. п. д. будет

что совпадает с ранее вычисленным значением.

Задачи

209. Чему равен термический к. п. д. цикла, если рабочее тело производит за цикл 5000 кгм работы, а количество отведенного тепла составляет 4 ккал?

210. Какую работу производит рабочее тело, совершающее круговой процесс, термический к. п. д. которого равен 0,37, если количество отведенного тепла составляет 10 ккал?

211. Определить параметры рабочего тела в характерных Точках цикла Карно, а также количество подведенного и отведенного тепла, работу и термический к. п. д. цикла, если известны максимальное и минимальное значения температуры t₁иt₃и давления р₁и р_3.Рабочее тело – воздух. Задачу решить в трех вариантах:

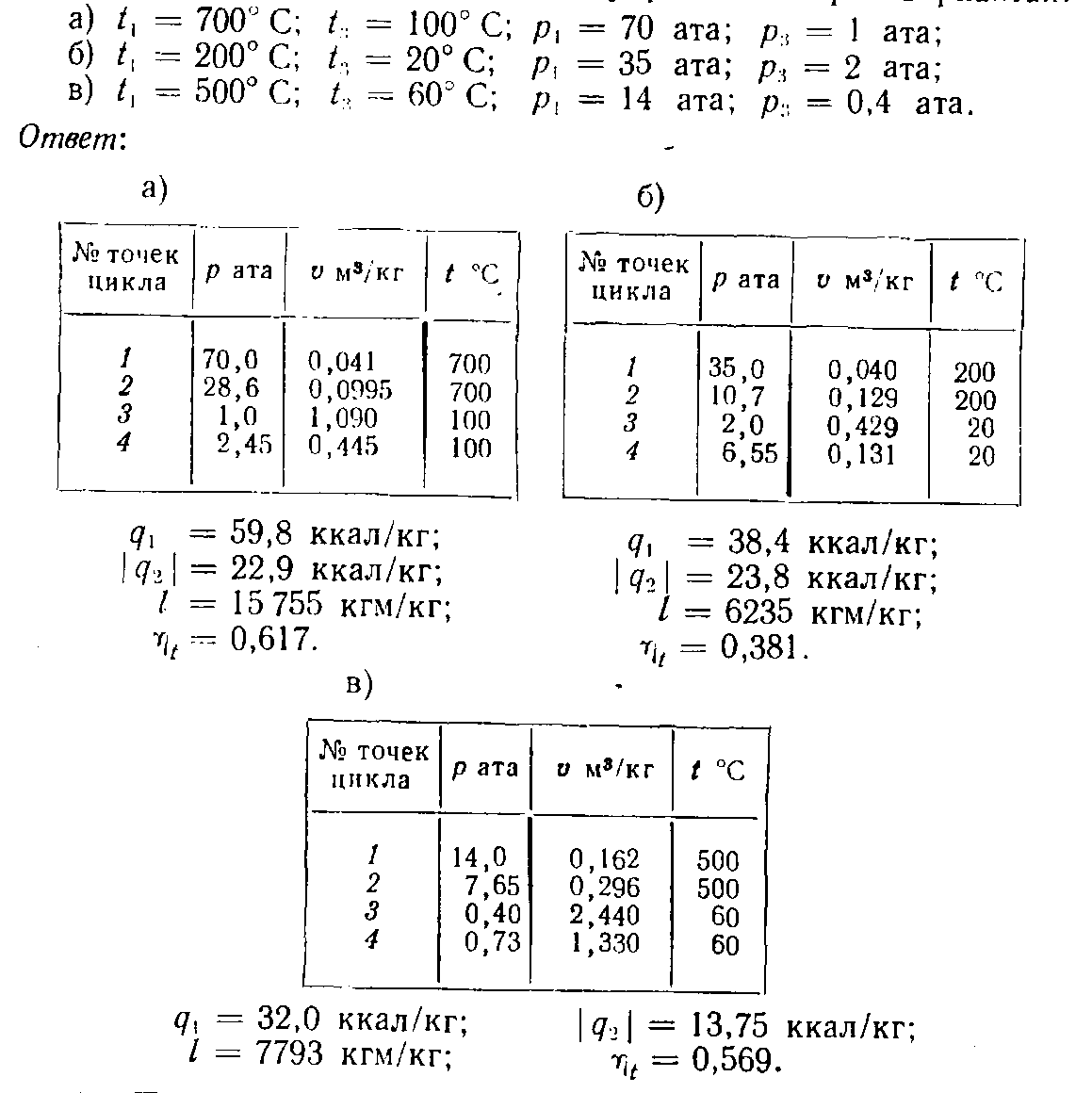
212. Построить график зависимости термического к. п. д. цикла Карно от Температуры теплоотдатчика t₁, если температура теплоприемника равна 0º С. Построение графика выполнить при изменении в пределах от 500° до 1500° С.

213. Построить график зависимости термического к. п. д. цикла Карно от температуры теплоприемника t₂, если температура теплоотдатчика равна 1000° С. Построение графика выполнить при измененииt₂в пределах от —50° до 500° С.

214. Некое рабочее тело совершает цикл Карно, получая тепло от теплоотдатчика, температура которого равна 320° С. Как изменится термический к. п. д. цикла, если температура и теплоотдатчика и теплоприемника повысится на 125° С? (Соответственно повысится и температура рабочего тела, так что цикл остается обратимым)

215. Определить термический к. п. д. цикла Карно, в котором при адиабатном расширении объем рабочего тела увеличивается в 4 раза. Рабочее тело воздух.

216. Решить предыдущую задачу для случая, если бы рабочим телом был углекислый газ (k= 1,31).

217. Определить термический к. п. д. и работу цикла Карно, если известно, что при изотермическом расширении объем рабочего тела увеличивается в 2,5 раза, а при адиабатном расширении — в 3,5 раза. Температура теплоприемника равна 17° С. Рабочее тело — окись углерода.

218. Чему равно отношение максимального и минимального объемов азота, совершающего цикл Карно, если работа цикла равна 12 000 кгм/кг, а его термический к. п. д. равен 0,56? Температура теплоприемника равна 27° С.

219. Определить работу и термический к. п. д. цикла Карно, если известно, что температура теплоприемника равна 0 °С, а объем рабочего тела в конце изотермического расширения и изотермического сжатия одинаков. Известно также, что количество отведенного тепла составляет 20 ккал/кг. Рабочее тело — кислород.

220. Определить термический к. п. д. и работу цикла Карно, если известно, что температура теплоприемника равна — 13°С, а давление рабочего тела в начале адиабатного расширения и адиабатного сжатия одинаково. Количество отведенного тепла составляет 15 ккал/кг. Рабочее тело — воздух.

221. Решить предыдущую задачу для случая, если бы рабочим телом был метан.

222. Определить работу и термический к. п. д. обобщенного цикла Карно, состоящего из двух изотерм и двух изобар (см. рис. 18), если известно, что температуры теплоотдатчика и теплоприемника равны соответственно 700° и 50° С, а отношение максимального и минимального давлений цикла равно 16. Рабочее тело — азот.

223. Чему равна работа и термический к. п. д. цикла Карно, если известно, что подведенное тепло составляет 40 ккал/кг? Известно также, что изотермическое сжатие рабочего тела осуществляется при температуре 9° С и при этом его энтропия уменьшается на 0,085 ккал/кг град.

224. Чему равна работа 1 кг воздуха, совершающего цикл Карно, если температуры теплоотдатчика и теплоприемника равны соответственно 20° и 880°С, а возрастание энтропии воздуха в процессе изотермического расширения составляет 0,073 ккал/кг град?

225. Определить работу и термический к. п. д. обобщенного цикла Карно, состоящего из двух изохор и двух изотерм, если энтропия рабочего тела при изохорном подводе тепла возрастает на 0,075 ккал/кг град, а при изотермическом подводе тепла возрастает на 0,102 ккал/кг град. Температура теплоприемника равна —10°С. Рабочее тело—кислород.

226. Определить термический к. п. д. и работу цикла, состоящего из двух изотерм и двух изохор, если максимальная и минимальная температуры цикла равны соответственно 1400° и 30° С, а степень сжатия (отношение наибольшего объема рабочего тела к его наименьшему объему) равна 6,5. Начертить схему цикла в координатах рvи Тs. Рабочее тело — азот.

227. Определить термический к. п. д. цикла, который состоит из следующих процессов: адиабаты сжатия 1—2, изобары расширения 2—3 и изохоры 3—1. Степень сжатия равна 2,0. Рабочее тело — воздух. Изобразить цикл в координатах рvи Тs.

228. Цикл состоит из политропьг сжатия 1—2, изобары расширения 2—3 и изохоры 3—1. Температура в начале сжатия равна 0° С, максимальная температура цикла равна 1500°С. Степень сжатия 4,0. Определить количество подведенного и отведенного тепла, работу и термический к. п. д. цикла. изобразить цикл в диаграммах рvи Тs. Рабочее тело — азот.

229. Цикл состоит из адиабаты сжатия 1—2, политропы сжатия 2—3 и изотермы расширения 3—1. Максимальная и минимальная температуры цикла равны соответственно 130° и 19° С. Отношение объемов в начале и конце тюлитропного сжатия равно 5,0. Определить количество подведенного и отведенного тепла. Изобразить цикл в диаграммах рvи Тs. Рабочее тело — кислород.

230. Определить работу и термический к. п. д. цикла, состоящего из политропы сжатия 1—2, изобары расширения 2—3 и изохоры 3—1. Известно, что количество тепла, отведенное при постоянном объеме, равно количеству тепла, подведенному при постоянном давлении. Наименьшая температура в цикле равна — 10°С, а наименьшее давление равно 0,4 ата. Степень сжатия 2,4. Рабочее тело — азот.

231. Между теплоотдатчиком (t₁= 800° С) и теплоприемником (t₂= 20° С) совершается цикл Карно. Количество подведенного тепла составляет 20 ккал. Температура рабочего тела в процессе изотермического подвода тепла равна 800°С, а в процессе изотермического отвода тепла равна 80°С. Определить термический к. п.д. цикла и потерю его работоспособности по сравнению с обратимым циклом Карно, совершающимся между теми же теплоотдатчиком и теплоприемником (при том же количестве подведенного тепла),

232. Между теплоотдатчиком (t₁= 450°С) и теплоприемником (t₂= 10°С) совершается цикл Карно. Температура рабочего тела в процессах изотермического подвода и отвода тепла равна соответственно 380° и 70°С. Определить потерю работоспособности цикла вследствие его необратимости, если количество подведенного тепла составляет 35 ккал.

233. Между теплоотдатчиком (t₁= 530°С) и теплоприемником (t₂= 30°С) совершается цикл Карно. Температура рабочего тела в процессах изотермического подвода и отвода тепла равна соответственно 450° и 100° С; количество работы, получаемой за цикл, равно 5000 кгм. Какое количество работы можно дополнительно получить за цикл (при том же количестве подведенного тепла), если бы удалось повысить температуру рабочего тела при подводе тепла до 500° С и понизить ее при отводе тепла до 50°С?

РАЗДЕЛ ДЕВЯТЫЙ

РАБОЧИЙ ПРОЦЕСС В КОМПРЕССОРЕ.

ТЕОРЕТИЧЕСКИЕ ЦИКЛЫ

ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ

И ГАЗОТУРБИННЫХ УСТАНОВОК

ПОРШНЕВЫЕ КОМПРЕССОРЫ

Теоретическая индикаторная диаграмма идеального одноступенчатого поршневого компрессора изображена на рис. 23. Процесс сжатия 1—2 в общем случае осуществляется по политропе. Если газ сжимается без отвода тепла, сжатие происходит по адиабате. Если охлаждение газа настолько интенсивно, что его температура в процессе сжатия вовсе не повышается, сжатие происходит по изотерме.

Работа L, потребляемая идеальным компрессором при изотермическом сжатии, равна

Тепло, отводимое в процессе изотермического сжатия, равно

Работа, потребляемая идеальным компрессором при политропном сжатии

В приведенных формулах V₁объем всасываемого газа в м³РаботаLпотребляемая идеальным компрессором при адиабатном сжатии, может быть определена, если вместо показателя политропыnподставить показатель адиабатыRРаботаL_адможет быть также определена по формуле

где G— вес >сжимаемого газа в кг:

i₁иi₂— энтальпия сжимаемого газа соответственно в начале и в конце процесса сжатия в ккал/кг.

В случае сжатия идеального газа формула эта принимает вид

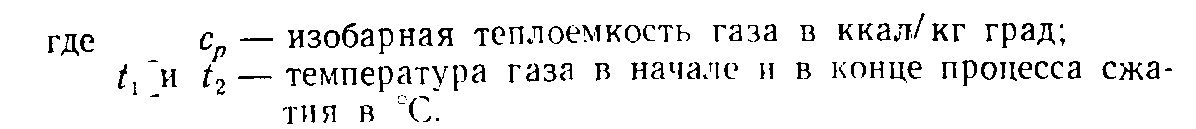
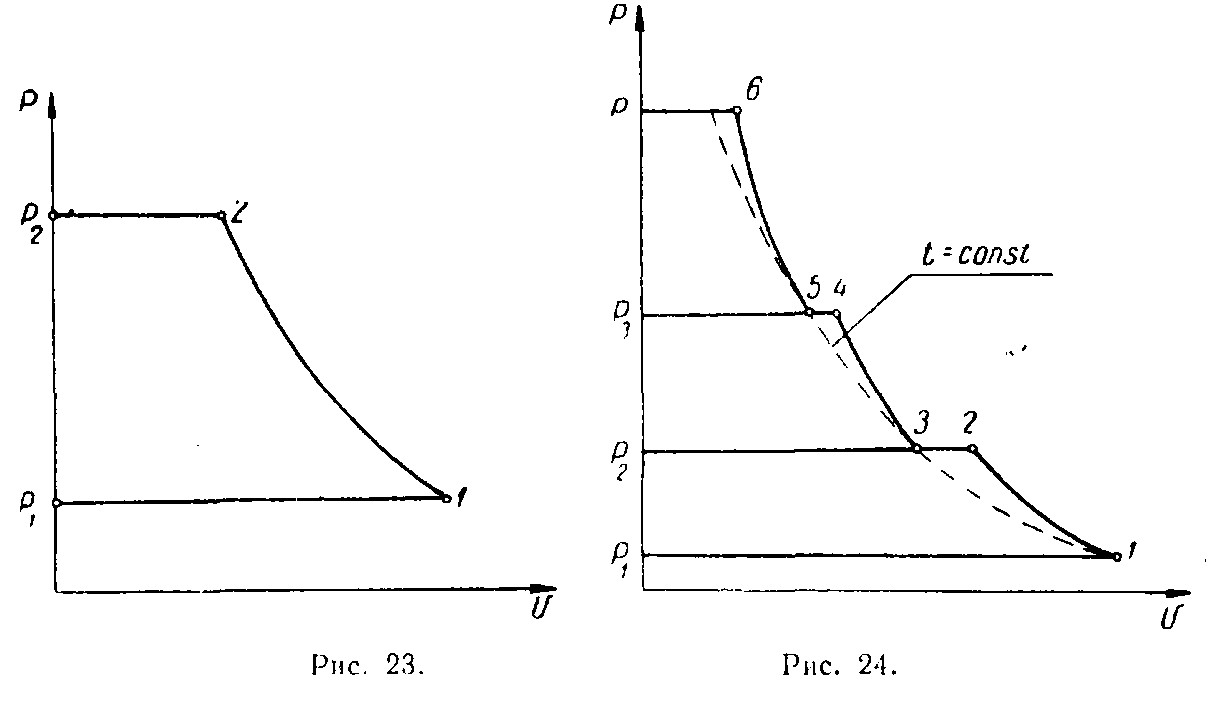
При производительности идеального компрессора V_nм³/час потребляемая им мощность определяется по формуле

На рис. 24 изображена индикаторная диаграмма идеального трехступенчатого поршневого компрессора. Охлаждение сжимаемого газа до первоначальной температуры t₁=t₃=t₅производится в промежуточных холодильниках при постоянном давлении. Наиболее экономичным является многоступенчатое сжатие при одинаковом для всех ступеней отношении давлений, т. е. при

В этом случае потребляемая работа L_ступдля всех ступеней

компрессора будет одинакова и определяется по приведенной выше

формуле при . Отношение давлений в одной ступени можно определить как

где m- число ступеней;

p₁— давление газа на входе в первую ступень:

р — давление газа на выходе из последней ступени.

Работа, потребляемая многоступенчатым компрессором

ДВИГАТЕЛИ ВНУТРЕННЕГО СГОРАНИЯ

В термодинамике рассматриваются следующие теоретические

циклы поршневых двигателей внутреннего сгорания:

а) цикл с изохорным подводом тепла (рис. 25 и 26);

б) цикл с изобарным подводом тепла (рис. 27 и 28);

в) цикл с изохорно-изобарным подводом тепла (рис. 29 и З0).

По циклу с изохорным подводом тепла работают карбюраторные и газовые двигатели, по циклу с изобарным подводом тепла работают компрессорные дизели, по циклу с изохорно-изобарным подводом тепла работают бескомпрессорные дизели.

Основными характеристиками цикла с изохорно-изобарным

подводом тепла являются следующие величины:

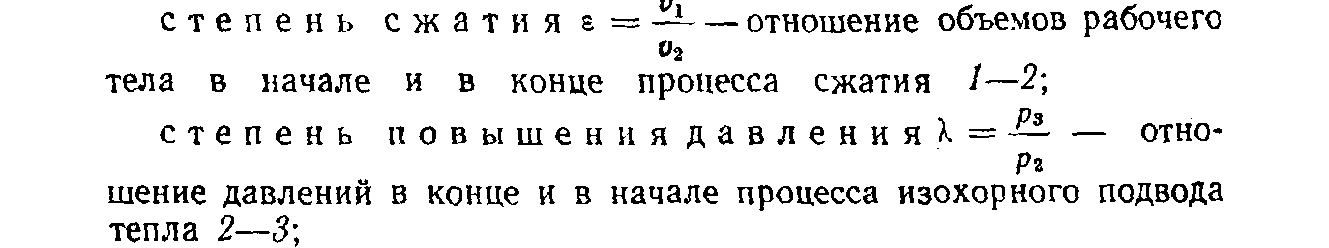
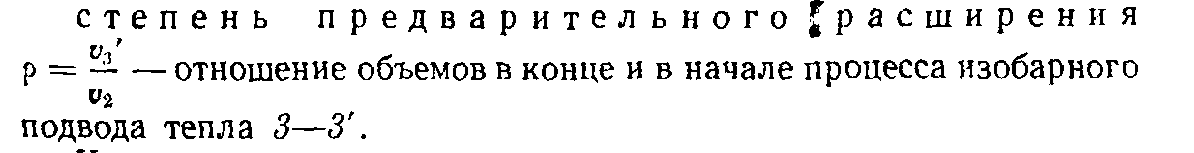
Количество подведенного тепла

количество отведенного тепла

работа, получаемая за цикл

термический к. п. д. цикла

Циклы с изохорным и с изобарным подводом тепла можно рассматривать как частные случаи цикла с изохорно-изобарным подводом тепла. Количество подведенного тепла в цикле с изохорным подводом тепла определяется как

В целях большего приближения теоретического цикла к действительным индикаторным диаграммам двигателей внутреннего сгорания процессы сжатия и расширения можно рассматривать не как адиабаты, а как политропы. При этом показатели политроп принимают равными их средним значениям, полученным при обработке действительных индикаторных диаграмм:

При расчете циклов, в которых сжатие и расширение рабочего тела происходит по политропам, необходимо при определении количества подведенного и отведенного тепла учитывать теплообмен в процессах сжатия и расширения.

ГАЗОТУРБИННЫЕ УСТАНОВКИ

Теоретический цикл газотурбинной установки (г. т. у.) с изобарным подводом тепла изображен на рис. 31 и 32. Характеристиками цикла являются: отношение объемов в начале и в конце сжатия (степень сжатия), отношение давлений в конце и в начале сжатия(степень повышения давления в компрессоре) и отношение объемов в конце и в начале изобарного подвода тепла(степень предварительного расширения).

Количество подведенного тепла

количество отведенного тепла

Работа и термический к. п. д. цикла определяются по ранее приведенным формулам. Для повышения экономичности г. т. у. вводят регенерацию, т. е. предварительный подогрев воздуха, сжатого в компрессоре и подаваемого в газовую турбину, за счет тепла отработавших газов. Теоретический цикл г. т. у с полной регенерацией показан на рис. 33.

Тепло, сообщаемое сжатому воздуху, изображается на этом рисунке площадью а- 2—4’- b. Оно равно теплу, отведенному

в регенераторе от отработавших газов, изображаемому площадью с—2’- 4 – d. Температура воздуха, поступающего в камеру сгорания, равна_,а температура уходящих газов равна .

В действительных условиях воздух в регенераторе нагревается до температуры t_5,несколько меньшей, чемt₄, а отработавшие газы охлаждаются до температурыt_6,,несколько выше, чемt₂.

Оценкой полноты регенерации является отношение

называемое степенью регенерации. При полной регенерации точки 5 и4 совпадают и тогда t₅=t_4.. В действительных установках σ = 0,5—0,7.

Количество подведенного тепла в цикле г. т. у. с регенерацией равно

количество отведенного тепла в этом цикле

Работа и термический к. п. д. цикла г. т. у. с регенерацией определяются как и для д. в. с.

Теоретический цикл г. т. у. с изохорным подводом тепла показан на рис. 34. Отношение называется степенью сжатия, отношение .— степенью добавочного повышения давления. Количество подведенного тепла равно

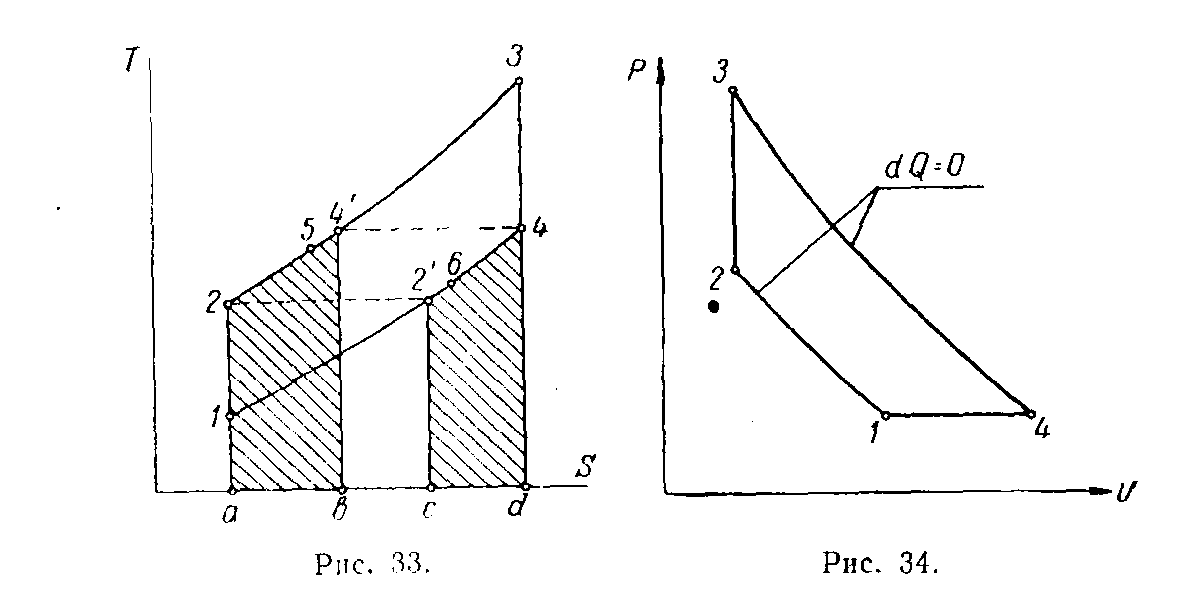
Пример. В двухступенчатом компрессоре происходит сжатие 450 м³/час воздуха от 1 ата до 40 ата. После сжатия в первой ступени воздух охлаждается в промежуточном холодильнике до начальной температуры, равной 20° С. Определить теоретическую мощность, потребляемую компрессором, и количество охлаждающей воды, прокачиваемой через промежуточный холодильник и через рубашки цилиндров компрессора, если температура охлаждающей воды повышается на 15° С. Сжатие воздуха в обеих ступенях происходит по политропе с показателем 1,25.

Решение. Индикаторная диаграмма обеих ступеней идеального компрессора изображена на рис. 35. Процесс охлаждения воздуха в промежуточном холодильнике представлен изобарой 2—2’.

Предполагая, что мощность, потребляемая каждой из ступеней, одинакова, определим отношение давлений на входе и на выходе для одной ступени

Работа, затрачиваемая на каждую ступень идеального компрессора в течение 1 часа

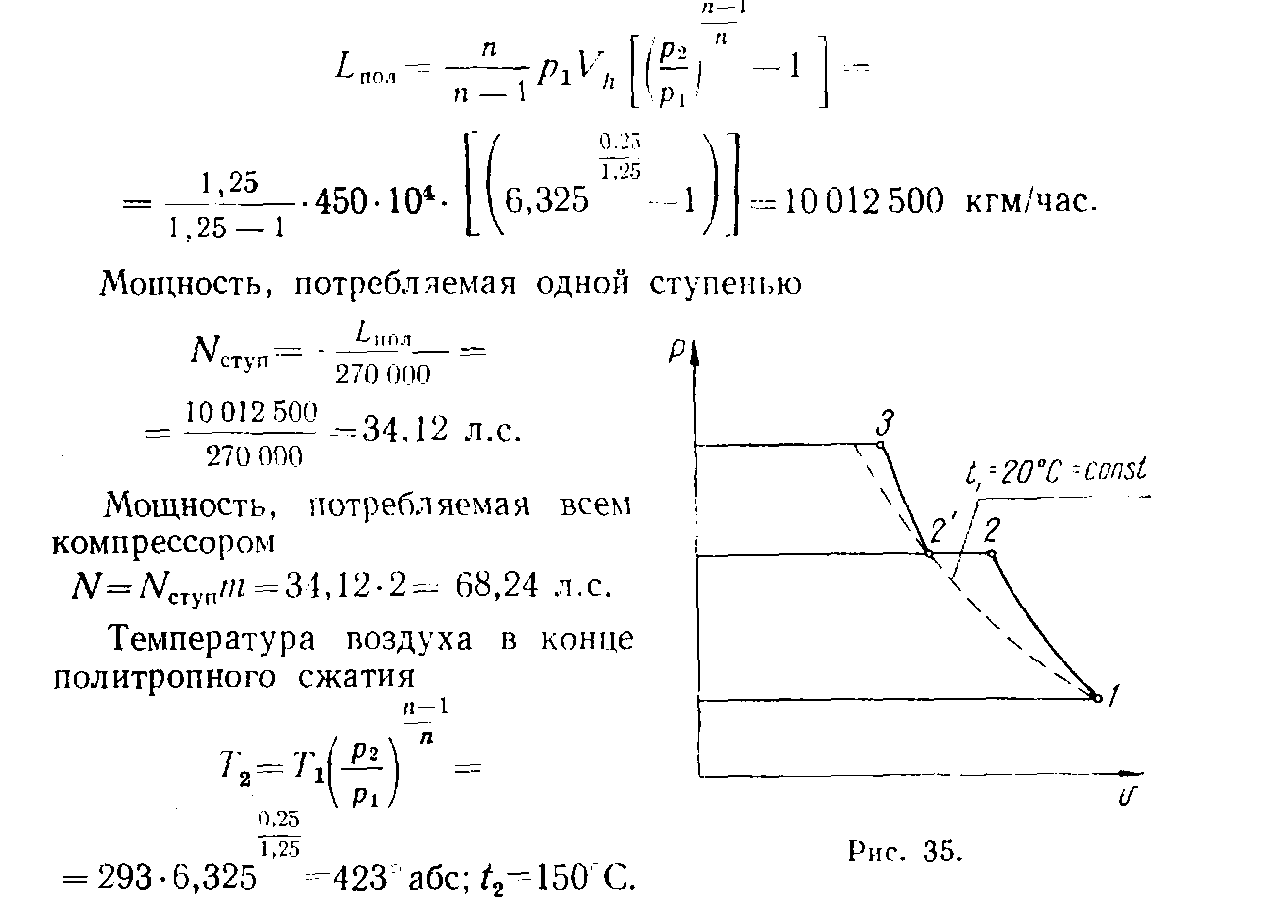
Весовое количество воздуха, сжимаемого в компрессоре

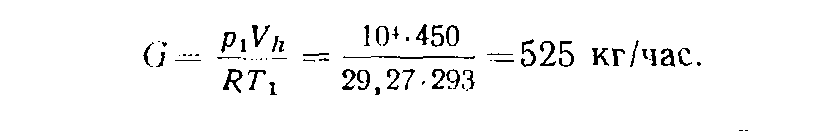
Количество тепла, отводимое от воздуха и одной ступени

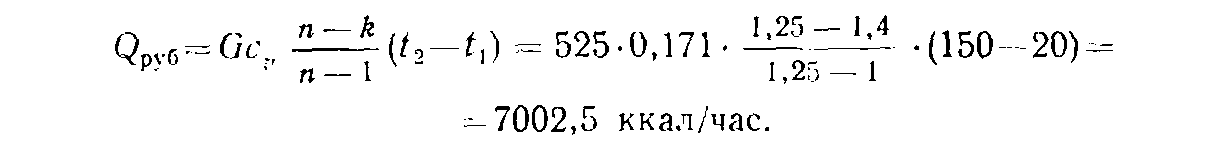
Количество охлаждающей воды, прокачиваемой через рубашку цилиндра одной ступени

Количество тепла, отводимого от воздуха в промежуточном холодильнике

Количество охлаждающей воды, прокачиваемой через холодильник

Общий расход охлаждающей воды на компрессор

Пример. Определить параметры в характерных точках цикла двигателя внутреннего сгорания с изобарным подводом тепла, если в начале сжатия давление и температура рабочего тела равны 1 ата и 20° С, степень сжатия степень предварительного

расширения р = 2,1. Сжатие происходит по политропе с показателем n₁= 1,35. а расширение по политропе с показателемn₂== 25. Определить также работу и термический к. п. д. цикла. Рабочее тело обладает свойствами воздуха. Теплоемкость считать постоянной.

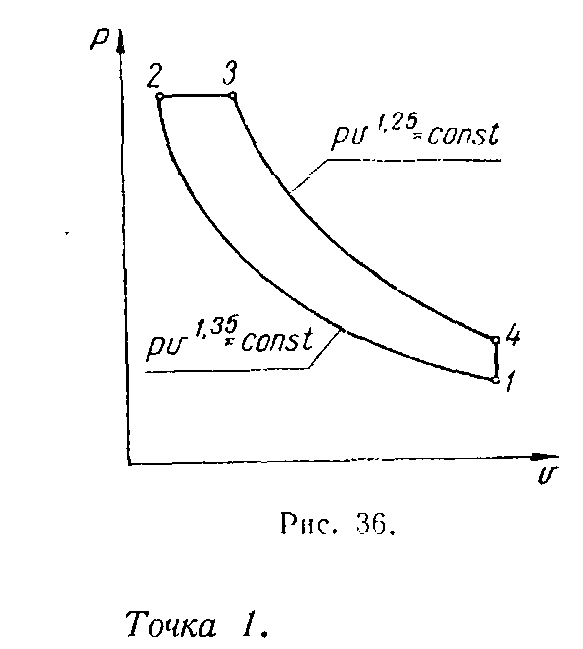
Из уравнения состояния идеального газа находим

Точка 2.

I1з уравнения политропы 1 – 2

Точка 3.

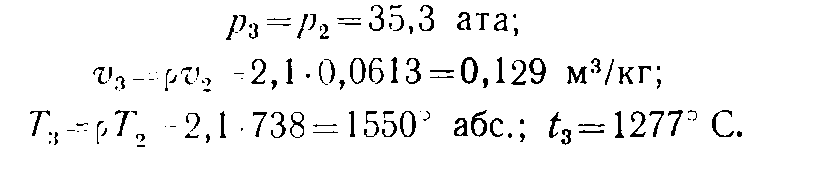
Точка 4.

Из уравнения политропы

Для удобства запишем найденные параметры характерных точек цикла в таблицу:

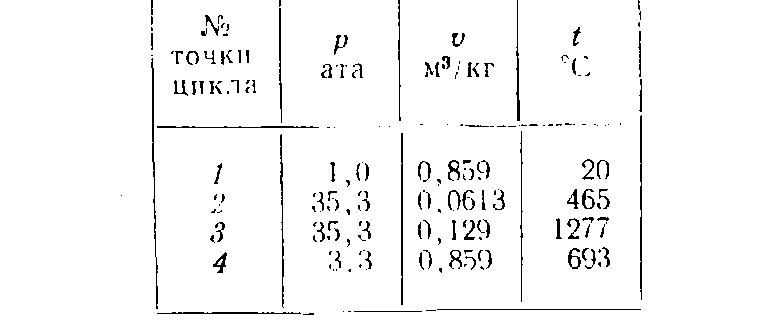
Теплоемкость воздуха

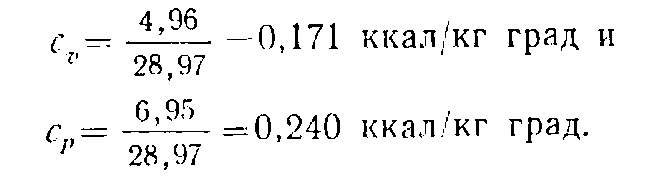
Тепло, участвующее в отдельных процессах, составляющих цикл

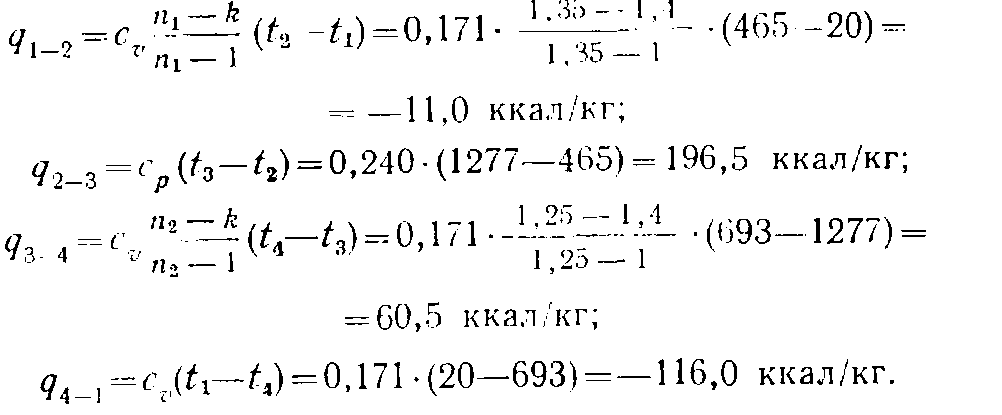
По знаку величин gустанавливаем, что тепло подводится в процессах 2—З и З—4, а отводится в процессах 1—2 и 4—1.

Количество подведённого тепла

количество отведенного тепла

Работа 1 кг рабочего тела, совершающего цикл

Термический к. п. д. цикла

Пример. Определить термический к. п. д. цикла д. в. с. с изохорно-изобарным подводом тепла, в котором общее количество подведенного тепла равно 260 ккал/кг, если давление и температура рабочего тела в начале сжатия равны 1 ата и 30° С, степень сжатия 12,0 максимальное давление цикла 65 ата, а сжатие и расширение происходит по адиабатам. Как изменится термический к. п. д. цикла, если при том же общем количестве подведенного тепла 15% этого тепла подводится в процессе расширения? (В действительном двигателе подвод тепла в процессе расширения имеет место при догорании горючей смеси в течение рабочего хода). Рабочее тело обладает свойствами воздуха. Теплоемкость считать постоянной.

Решение. Изображение рассматриваемого цикла представлено на рис. 29. Определим его термический к. п. д., для чего необходимо определить температуру в точке 4 и затем вычислить количество отведенного тепла.

Из уравнения адиабаты имеем

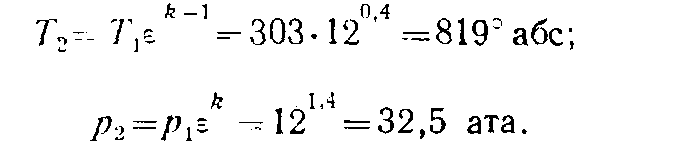
Количество тепла, подведённого в изохорном процессе 2—3 (значения теплоемкостей с_pи с_vвоздуха определены в предыдущем примере)

Количество тепла, подведенного в изобарном процессе 3—З’

Температура в точке 3’

Степень предварительного расширения

Температура в точке 4 (из уравнения адиабаты 3’-—4)

Количество отведенного тепла в цикле с адиабатным расширением

Термический к. п. д. цикла с адиабатным расширением

В цикле, где часть тепла подводится в процессе расширения, расширение происходит по политропе. Так как максимальное давление цикла (давление в точках 3 и 3’) остается прежним, то, q_1vиT₃ также остаются прежними. Величины жеq_1риизменяются. Следовательно, изменяется также Т₄а значит, и количество отведенного тепла. Определим значения этих величин для цикла с политропным расширением.

Количество тепла, подведенного в изобарном процессе 3—3’

Температура в точке 3’

Степень предварительного расширения

Для определения температуры в точке 4 необходимо решить систему уравнений, а именно: уравнение политропы 3’—4

и выражение для количества тепла, переданного в политропном процессе

из которого получаем

где n— показатель политропы расширения.

Подставляя в них значения известных нам величин, получим

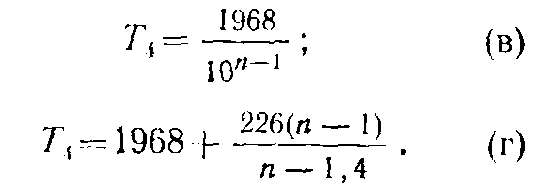
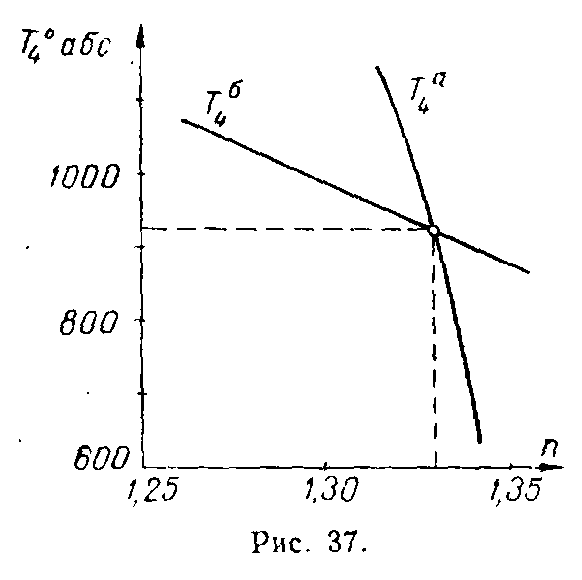
Решаем эту систему уравнений графическим путем, для чего задаемся значениями показателя политропы nи вычисляем значения температуры в точке 4. По результатам вычислений строим кривыеи. Это построение приведено на рис. 37. Точка пересечения кривых определяет значение Т₄, а одновременно и значение показателяnполитропы расширения. Как видно из рис. 37, Т₄ ≈ 925° абс. иn= 1,329.

Количество отведенного тепла в цикле с политропным расширением

Термический к. п. д. цикла с политропным расширением

Таким образом, вследствие того, что часть тепла подводится в процессе расширения. термический к. п. д. цикла уменьшился на

Пример. Построить график зависимости термического к. п. д. цикла д. в. с. с изобарным подводом тепла (см. рис. 36) от степени предварительного расширения ρ при ε = 12; 14; 16 иk= 1,4. Построение выполнить для значений ρ от 1,5 до 2,5.

Р е ш е н и е. Термический к. п. д. рассматриваемого цикла равен

Для построения графика подставляем в приведенную формулу различные значения ε и ρ и вычисляем соответствующие им значения . Результаты вычислений сводим в таблицу:

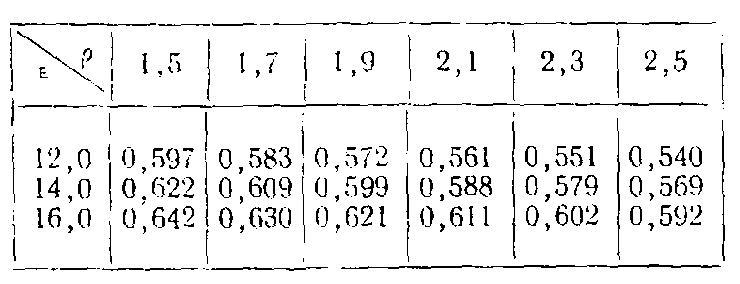
По полученным значениям _t, строим график (рис. 38). Как видно из графика термический к. п. д. цикла д. в. с. с изобарным подводом тепла повышается с повышением степени сжатия ε и с уменьшением степени предварительного расширения ρ.

П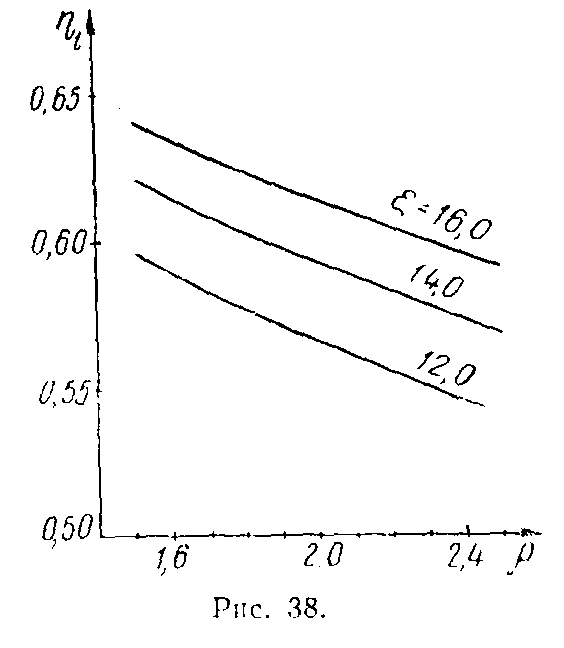ример. Газотурбинная установка работает по циклу с изобарным подводом тепла (рис. 31). Максимальная и минимальная температуры цикла равны соответственно 1000° и 20° С; степень сжатия равна 4,0. Определить термический к. п. д. цикла. Как изменится термический к. п. д. цикла в результате введения частичной регенерации тепла (при σ = 0,6)? Рабочее тело — воздух. Теплоемкость считать постоянной.

Р е ш е н и е. Для определения термического к. п. д. цикла необходимо определить количество подведенного и отведенного тепла, для чего следует вычислить температуры в характерных точках цикла. Температура в начале сжатия задана: t₁= 20° С. Из уравнения адиабаты сжатия 1—2 находим¹

Температура в точке 3 также известна: t₃= 1000° С. Из уравнения адиабаты расширения находим²

Теплоемкость воздуха в изобарном процессе

Количество подведенного тепла

Количество отведенного тепла

Термический к. п. д. цикла г. т. у. без регенерации тепла

Цикл г. т. у. с изобарным подводом тепла при наличии частичной регенерации тепла схематически показан на рис. 33. В этом случае количество подведенного тепла

а количество отведенного тепла

Термический к. п. д. цикла г. т. у. с регенерацией тепла

Таким образом, в результате введения частичной регенерации тепла термический к. п. д. цикла г. т. у. увеличился на 0,544-0,423=0,121 или 0,121/0,423100=28,6%.

Задачи

234. Компрессор всасывает V_hм³/ч воздуха при давлении р₁ата и сжимает его изотермически до давления р₂ата. Определить теоретическую мощность, потребляемую компрессором, и количество охлаждающей воды, прокачиваемой через рубашку цилиндра компрессора, если температура воды повышается на 15° С. Задачу решить в следующих вариантах:

235. Компрессор всасывает V_hм³/ч воздуха при давлении р₁ата и температуре °С и сжимает его до давления р₂ата. Определить мощность, затрачиваемую на работу идеального компрессора, и температуру сжатого воздуха, если сжатие осуществляется по

адиабате.

236. Идеальный компрессор всасывает 600 м³/час воздуха при давлении 1 ата и сжимает его до давления 6,5 ата. Определить мощность, затрачиваемую на компрессор, если сжатие происходит:

а) по изотерме; 6) но политропе с показателем n= 1,3; в) по адиабате.

237. Мощность, затрачиваемая на идеальный компрессор, составляет 40 л. с. Какое количество воздуха, сжатого до 7 ата, можно получить: а) при изотермическом сжатии; б) при политропном сжатии с показателем n= 1,2? Давление всасываемого воздуха равно 1 ата. Считать, что сжатый воздух на выходе из компрессора охлажден до начальной температуры (при политропном сжатии).

238. Предельное значение температуры, получаемое при сжатии газа в компрессоре, определяется свойствами масла, применяемого для смазки цилиндров компрессора³. Принимая предельное значение температуры равным 150° С. определить, до какого давления можно сжать 250 м³воздуха в идеальном одноступенчатом компрессоре, если через рубашку цилиндра компрессора прокачивается 465 кг/час воды. Температура воды при прохождении через рубашку цилиндра повышается на 14° С. давление и температура всасываемого воздуха равны Р₁= 1 ата,t₁= 20° С. Определить также мощность, потребляемую компрессором.

239. На какое давление должен быть отрегулирован предохранительный клапан на цилиндре идеального компрессора, если предельное значение температуры составляет 130° С? Компрессор всасывает 190 м³/час воздуха при давлении 1,03 ата в температуре 17° С. Нагрев воды, циркулирующей в зарубашечном пространстве цилиндра, равен 15° С, а расход охлаждающей воды составляет:

а) 400 кг/час; 6) 200 кг/час; в) охлаждение цилиндра не производится.

240. В идеальном компрессоре производится адиабатное сжатие 270 нм³/час воздуха. Определить мощность, потребляемую компрессором, если температура воздуха при сжатии возрастает от 30° до 165° С.

241. Чему равна производительность идеального компрессора, потребляющего мощность 20 л. с., если температура всасываемого воздуха равна 15° С. а температура сжатого воздуха не должна превышать 140° С? Сжатие воздуха в компрессоре происходит по адиабате.

242. В двухступенчатом идеальном компрессоре происходит сжатие 350 м³воздуха от 1 ата до 35 ата. После сжатия в 1-й ступени воздух охлаждается в промежуточном охладителе до начальной температуры, равной 20° С. Определить мощность, потребляемую компрессором, и количество охлаждающей воды, прокачиваемой через охладитель и рубашки цилиндров компрессора, если температура воды повышается на 15° С. Сжатие воздуха в обеих ступенях происходит по политропе с показателемn= 1,25.

243. В трехступенчатом идеальном компрессоре происходит сжатие 500 м³/час воздуха от 1 ата до 120 ата. Сжатие воздуха во всех ступенях осуществляется по адиабате. После сжатия в первых двух ступенях воздух охлаждается в промежуточных холодильниках до начальной температуры равной 25° С. Определить мощность, затрачиваемую на компрессор, в количество охлаждающей воды, прокачиваемой через холодильники, если температура воды повышается на 15° С.

244. Определить мощность, потребляем двухступенчатым идеальным компрессором при сжатии 280 м³воздуха от 1 ата до 7 ата. Начальная температура воздуха 12° С. После сжатия в 1-й ступени воздух охлаждается в промежуточном холодильнике до начальной температуры. Какую мощность пришлось бы затрачивать на такое же сжатие этого же количества воздуха в одноступенчатом идеальном компрессоре? Определить температуру воздуха в конце сжатия в одно и в двухступенчатом компрессоре. Сжатие воздуха в обеих ступенях двухступенчатого компрессора и одноступенчатом компрессоре считать адиабатным.

245. Определить параметры в характерных точках цикла д. в. с. с изохорным подводом тепла, если известны давление Р₁и температураt₁рабочего тела в начале сжатия, степень сжатия ε и степень повышения давления. Определить работу, получаемую от цикла, и его термический к. п. д. Сравнить термический к. п. д. данного цикла и цикла Карно, совершаемого в том же температурном интервале. Рабочее тело — воздух. Теплоемкость считать постоянной.

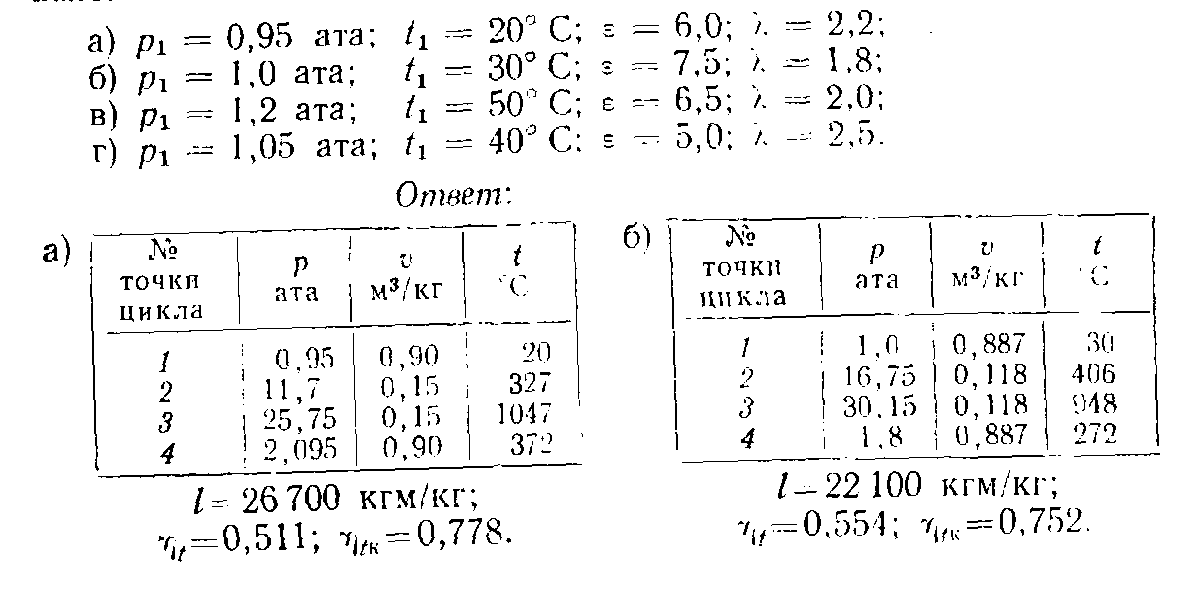
246. Определить параметры в характерных точках цикла д. в. с. с изобарным подводом тепла, если известны давление р₁и температураt₁рабочего тела в начале сжатия, степень сжатия и степень предварительного расширения ρ.

Определить также работу, получаемую от цикла, и его термический к. п. д. Сравнить термический к. п. д. данного цикла и цикла Карно, осуществляемого в том же температурном интервале. Рабочее тело — воздух. Теплоемкость постоянна.

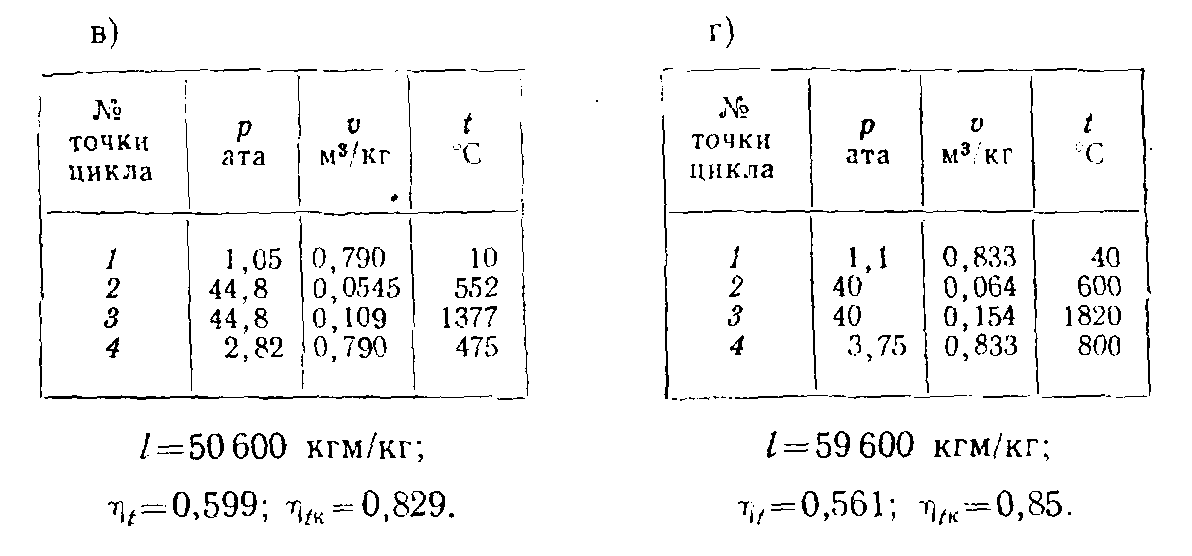
247. Определить параметры в характерных точках цикла д. в. с. с изохорно-изобарным подводом тепла, если известны давление р₁ и температураt₁рабочего тела в начале сжатия, степень сжатия ε, степень предварительного расширения ρ и степень повышения

давления . Определить работу, получаемую от цикла, и его термический к. п. д. Сравнить термические к. п. д. заданного цикла и цикла Карно, осуществляемого в том же температурном интервале. Рабочее тело — воздух. Теплоемкость считать постоянной.

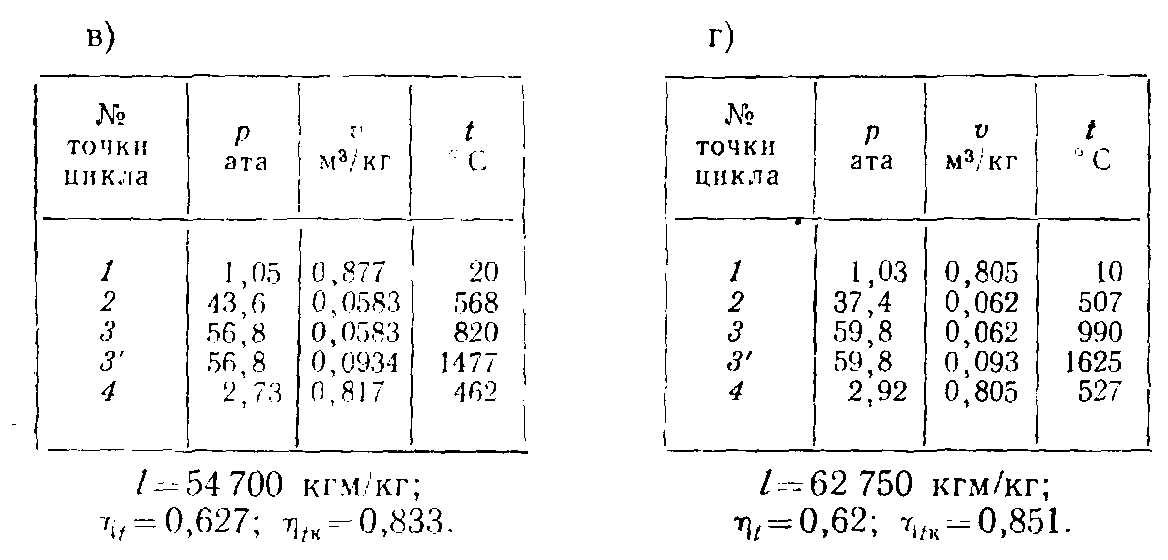
248. Определить работу и термический к. п. д. цикла д. в. с. с изохорным подводом тепла, если в начале сжатия давление равно 1 ата., а в конце процесса подвода тепла давление равно 28 ата и температура равна 1200° С. Количество подведенного тепла составляет 95 киал/кг. Рабочее тело — воздух. Теплоемкость считать постоянной.

249. Определить параметры в характерных точках цикла д. в. с. с изохорным подводом тепла, если в начале сжатия давление и температура рабочего тела равны 1 ата и 60° С. Определить также работу, получаемую от цикла, и его термический к. п. д. Принять, что сжатие происходит по политропе с показателем n₁= 1,33, а расширение по политропе с показателемn₂= 1,25. Степень сжатия 8,0; степень повышения давлении 1,8. Рабочее тело – воздух.

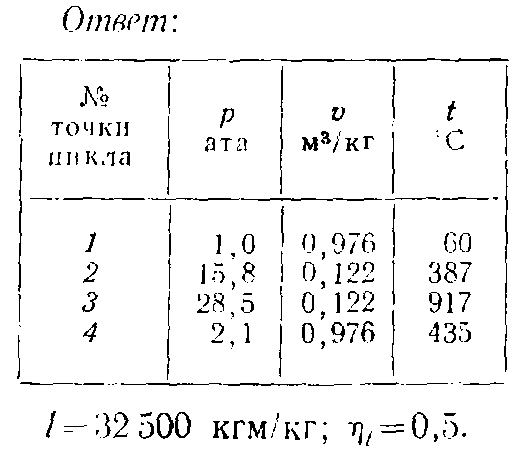
250. Определить параметры в характерных точках цикла д. в. с. с изохорно-изобарным подводом тепла, если в начале сжатия давление и температура рабочего тела равны 1,05 ата и 50° С степень сжатия 13,0; степень повышения давления 1,7; степень предварительного расширения 1,3. Сжатие происходит по политропе с показателем n₁= 1,37, а расширение — по политропе с показателемn₂= 1,28. Определить работу, получаемую от цикла, и его термический к. п. д. Рабочее тело - воздух Теплоемкость считать постоянной.

251. В цикле д. в. с. с изохорно-изобарным подводом тепла часть тепла q_1vподводится изохорно и часть теплаq_1рподводится изобарно. Построить график зависимости термического к. п. д. цикла_tот доли тепла, подведенного изохорно,, если общее количество подведенного тепла составляетq₁=q_1v+q_1p=200 ккал/кг, а степень сжатия равна 12,5. Давление и температура рабочего тела в начале сжатия равны 1 ата и 40° С. Рабочее тело—воздух. Теплоемкость считать постоянной.

У к а з а н и е. Построение графика выполнить для значений от 0 до 0,50. Процессы сжатия и расширения считать адиабатными.

252. Определить термический к. п. д. цикла д. в. с. с изобарным подводом тепла, если количество подведенного тепла составляет 280 ккал/кг, температура рабочего тела в конце сжатия 450°С, степень сжатия 12, а сжатие и расширение происходят по адиабатам. Как изменится термический к. п. д. цикла, если при том же общем количестве подведенного тепла 25% этого тепла подводится в процессе расширения? Рабочее тело — воздух. Теплоемкость считать постоянной.

253. Определить работу и термический к. п. д. цикла г. т. у. с изобарным подводом тепла (рис. 31), если степень сжатия ра вна 4,0, а максимальная и минимальная температуры Цикла равны соответственно 950°С и 30°С. Рабочее тело—воздух. Теплоемкость считать постоянной.

254. Сравнить термический к. п. д. следующих циклов г. т. у. с изобарным подводом тепла: а) без регенерации тепла; б) с частичной регенерацией тепла при степени регенерации σ = 0,5: в) с полной регенерацией тепла (σ = 1,0). Степень сжатия равна 3,5; максимальная я минимальная температуры равны соответственно 900° и 30° С. Рабочее тело—воздух.

255. Определить параметры в характерных точках цикла г. т. у. с изохорным подводом тепла (рис. 34), если давление и температура в начале сжатия равны 1 ата и 30° С; степень сжатия 4,5; максимальная температура цикла 1200° С. Определить также работу, получаемую за цикл, и его термический к. и. д. Рабочее тело – воздух. Теплоемкость считать постоянной.

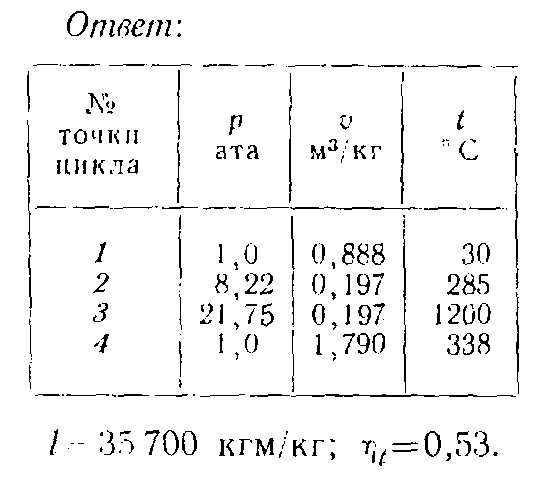
РАЗДЕЛ ДЕСЯТЫЙ

ВОДЯНОЙ ПАР

Состояние сухого насыщенного пара определяется одним независимым параметром. Наиболее часто за параметр, определяющий состояние сухого насыщенного пара, принимается давлен под которым находится пар.

Между давлением насыщенного пара р (давлением насыщения и температурой кипения t_sимеется зависимость

определяемая опытным путем. Иными словами, каждому значению давления р соответствует строго определенное значение температуры кипения t_sПараметры сухого насыщенного пара в зависимости от давления даны в приложении 9.⁴

Состояние сухого насыщенного пара является неустойчивым (пограничным): как угодно малый отвод тепла превращает сухой насыщенный пар во влажный, а столь же малый подвод тепла вызывает его перегрев.

Влажный пар является двухфазной системой. Каждая фаза (жидкость и сухой пар) находится в термодинамическом равновесии, т. е. находится при одинаковой температуре t_sи давлении р.

Степенью сухости х влажного пара называется отношение веса сухого пара к весу смеси; последняя, как указывалось, состоит из жидкости в сухого пара этой жидкости. Величина х меняется от нуля (жидкость при температуре кипения) до единицы (сухой насыщенный пар).

Удельный объем влажного пара

энтальпия влажного пара

энтропия влажного пара

где v’,i’ иs’ - Соответственно удельный объем, энтальпия и энтропия жидкости при температуре кипенияt_s. Указанные величины даны в приложении 9.

В ряде технических задач при х>0,7 (исключая область состояний, близкой к критической точке) можно пользоваться приближенной формулой

Количество тепла q, необходимое для нагревания при постоянном давлении 1 кг воды от 0ºС до температуры кипения, с достаточной степенью точности может быть принято равным значению энтальпии водыi’

Затрата тепла на получение 1 кг сухого насыщенного пара из воды с начальной температурой 0° С при ее нагревании при р = constс той же степенью точности может быть принятой равной энтальпии i’’

Состояние перегретого пара определяется двумя любыми термодинамическими параметрами (подобно газам). Таблицы перегретого пара составлены так, что в зависимости от Давления и темпера туры Даны значения удельного объема vм³/кг энтальпии i ккал/кг и энтропииsккал/кг град (приложение 10).

Процесс перегрева пара обычно рассматривается как процесс при р = const. Количество тепла, затрачиваемое на перегрев пара от температурыt_sдоt, определяется по формулам:

В ряде задач необходимо определить внутреннюю энергию пара в заданном состоянии⁵. Последняя всегда определяется по формуле

Параметры i, р иvопределяются из таблиц или с помощью диаграммыis.

ДИАГРАММА is

Сложность уравнения состояния перегретого нара и отсутствие такого уравнения для насыщенного пара вызывает необходимость при изучении процессов с парами пользоваться указанными выше таблицами. Однако решение ряда задач с помощью таблиц требует применения метода последовательных приближений и связано

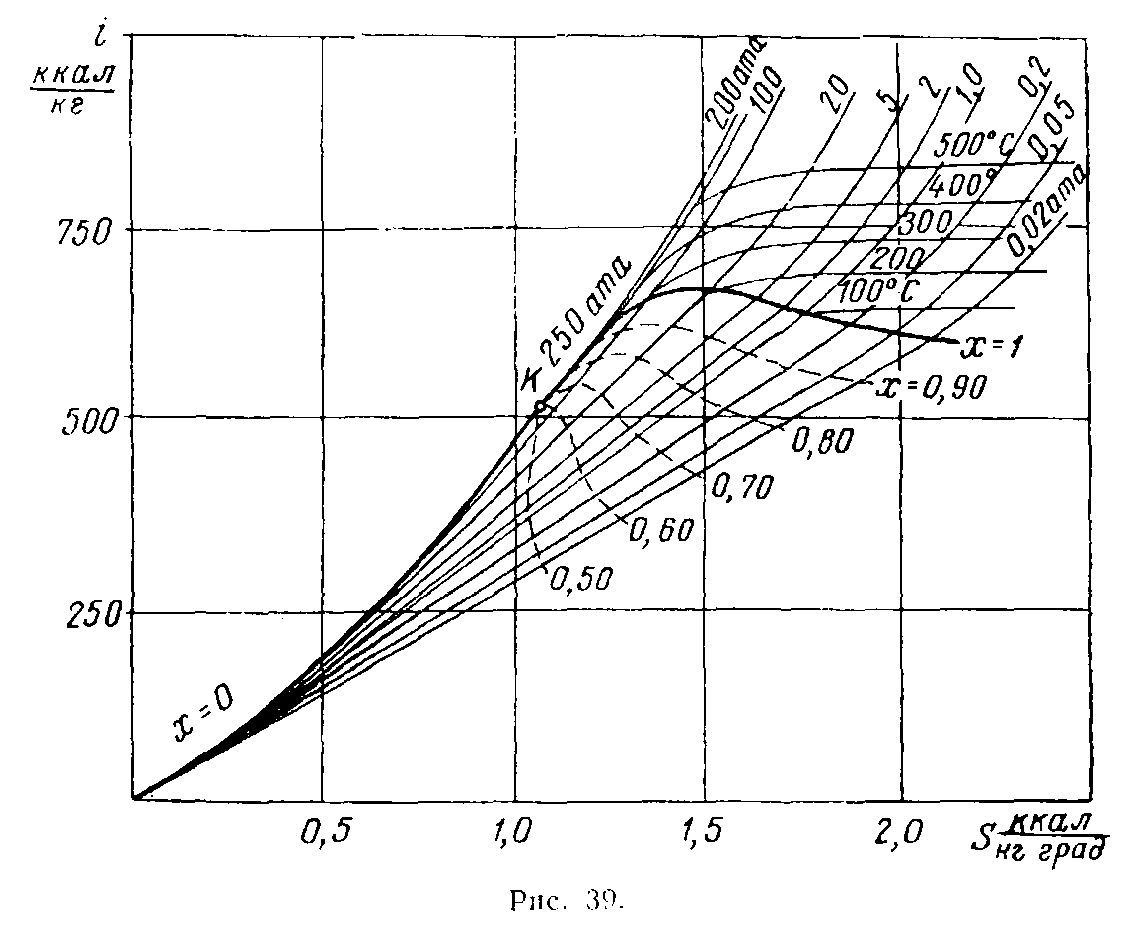
с трудоемкими вычислениями. Поэтому в технических расчетах с парами получила широкое распространение диаграмма is. На диаграмме is(рис. 39) нанесены: нижняя пограничная кривая х = 0 и верхняя пограничная кривая х = 1. Критическая точка К в этой диаграмме находится на левом склоне пограничных кривых. На диаграмме нанесены изобары, изотермы, изохоры, а в области влажного пара - линии постоянной сухости нара. В области влажного пара изобары и изотермы совпадают, при переходе в область перегретого пара они разветвляются и представляют каждая отдельную кривую. Обычно используемая для расчетов диаграмма isохватывает не всю область насыщения, а только часть ее вблизи верхней пограничной кривой. Поэтому все расчеты при х<0,65 производятся с помощью таблиц водяного пара.

ПРОЦЕССЫ С ПАРАМИ

Отсутствие практически удобного уравнения состояния пара вызывает необходимость при изучении процессов с парами непосредственно использовать общие зависимости термодинамики, не связанные с уравнением состояния. Такими зависимостями для обратимых изменений состояния являются:

Первый закон термодинамики

или

второй закон термодинамики

и, наконец, математическое определение понятия энтальпия.

К этим общим зависимостям присоединяется условие, определяющее особенность рассматриваемого процесса (v=const.P=constи тп.).

Исходя из этих предпосылок получим следующие расчетные формулы для определения тепла q, участвующего в процессе полученной (или затраченной) работы 1 и приращения внутренней энергии ∆u.

Изохорггый процесс (v=constилиdv=0). Так как l=0, то

Если процесс полностью или частично протекает в области влажного пара, то, исходя из условия v₁=v₂=v, легко определить степень сухости пара в конце (начале) процесса. При использовании диаграммыisстепень сухости х определится непосредственно на днаграмме.

И з о б а р н ы й п р о ц е с с (р=constилиdр=0).

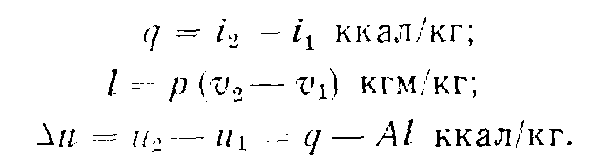
Если процесс протекает в области влажного пара, то изобарный процесс является одновременно и изотермическим. В этом случае можно воспользоваться и следующей формулой:

Для влажного пара удельный объем в зависимости от степени сухости может быть определен вычислением или по диаграмме is.

Изотермический процесс (t=constилиdt=0)

изотермический процесс в области влажного пара совпадает с изобарным процессом

Для изотермического процесса в области перегретого пара используются формулы

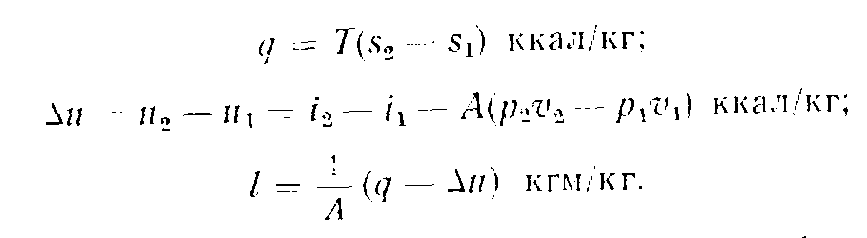
Адиабатный процесс (s=constилиds=0) Для адиабатного процессаdq=0 иAdl=-du. Следовательно

Приближенное уравнение адиабаты имеет вид

Показатель адиабаты принимается равным для перегретого пара k=1,3; для сухого насыщенного параk=1,135 и для влажного пара с начальной степенью сухости х,k=1,0.35+0,1х. Более правильным является определение показателя адиабатыkпо формуле

находим

Д р о с с е л и р о в а н и е п а р а. Принимается, что в процессе дросселирования начальное и конечное значения энтальпии одинаковы, т. е. i₁=i₂. При этом условии процесс дросселирования на диаграммеisусловно изображается горизонтальным отрезком (истинному состоянию пара соответствует только начальная и конечная точки этого отрезка).

Пример. Определить температуру, удельный объем, энтальпию, энтропию и внутреннюю энергию водяного пара при р = 64 ата и х = 0,95, используя таблицы водяного пара и диаграмму is.

Р е ш е н и е. Используя таблицы водяного пара (приложение 9), находим

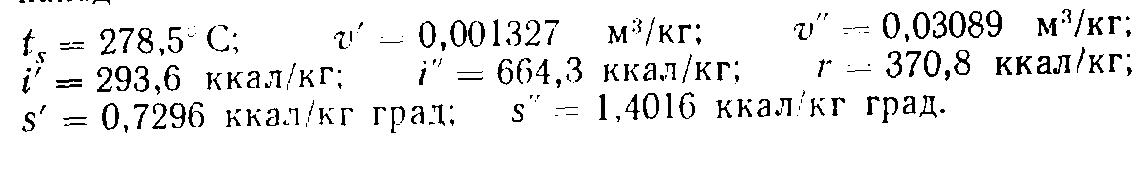
Удельный объем влажного пара определяется по формуле

Используя приближенную формулу, получим

Точность расчета по приближенной формуле в данном случае вполне достаточна.

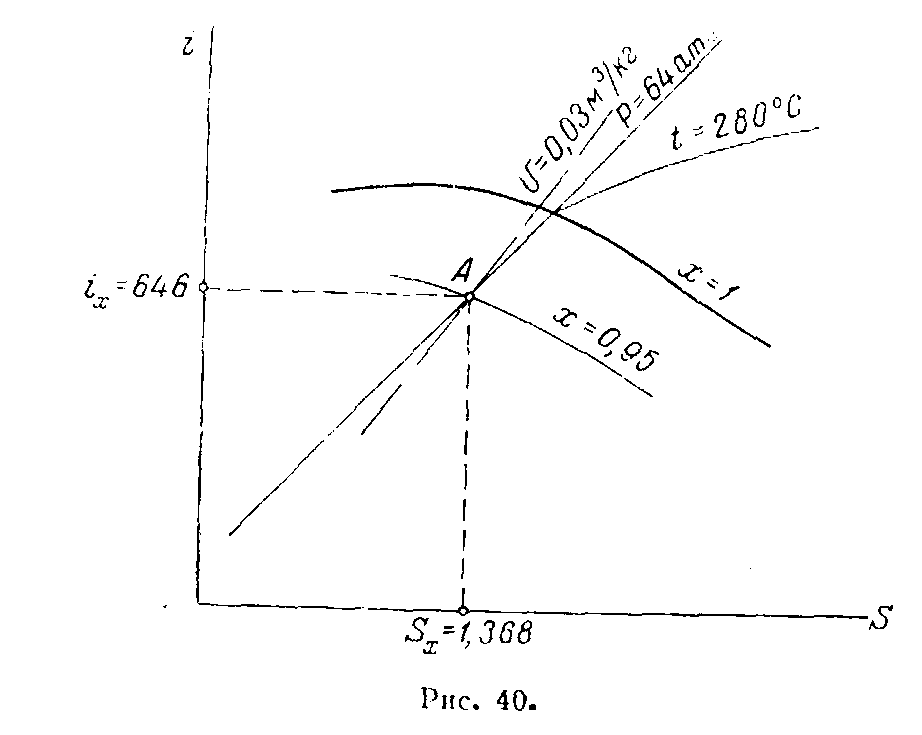
Энтальпия влажного пара определяется по формуле

а энтропия

Определяем внутреннюю энергию влажного пара

Пользуясь диаграммой is, Находим точку А на пересечении изобары р=64 ата с линией постоянной сухости х=0,95 (рис. 40). Проектируя точку А на ось ординат, определим значение энтальпииi_x= 646 ккал/кг; проектируя ее на ось абсцисс, находим значение энтропииs_x= 1,368 ккал/кг град. Для определения температуры пара находим точку пересечения изобары р = 64 ата с верхней пограничной кривой. Через эту точку проходит изотермаt= 280° С. Это и есть температура пара в точке А. Значение удельного объема пара в точке А определяется по изохоре. проходящей через эту точку:v_x= 0,03 м³/кг Значение внутренней энергии пара в точке А определяется по формуле

Пример. Используя таблицы водяного пара, определять состояние пара при давлении Р= 16 ата, если удельный объем равен: а) v= 0,11 м³/кг б)v= 0.155 м³/кг

Р е ш е н и е. Для того, чтобы определить, в каком состоянии находится пар, необходимо сопоставить заданные значения объемов с объемом v” сухого насыщенного пара при давлении 16 ата. По таблице (приложение 9) находим:v” = 0,1261 м³/кг.

а) Так как в первом случае v”>v, то пар влажный. Степень сухости пара находим, пользуясь уравнением

б) Во втором случае v”<v, следовательно, пар перегретый. По таблице перегретого пара по Давлению р= 16 ата иv= 0,155 м³/кг определяем температуру пара:t= 280° С.

Пример. Определить вес, энтальпию и внутреннюю энергию 5 м³водяного пара при давлении 10 ата и температуре 260° С.

Р е ш е н и е. давлению 10 ата соответствует температура t_s= 179° С (приложение 9). Следовательно, в заданном состоянии пар перегретый.

По таблице Для перегретого пара находим

Вес пара

Энтальпия пара

Внутренняя энергия пара

Пример. В паровом котле, имеющем пароводяной объем 4,5 м³при рабочем давлении 28 ата и температуре насыщения находится 3,7 м³воды. Определить степень сухости х и весовое количество пара.

Р е ш е н и е. используя таблицы водяного пара (приложение 9), находим

Весовое количество воды в котле

Весовое количество пара в котле

Степень сухости

Пример. Определить тепло, затрачиваемое на подогрев 1 кг воды от 0° С до температуры кипения, с учетом отклонения изобары от нижней пограничной кривой при давлении: а) Р₁= 1 ата; б) Р₂=10 ата; в) Р₃= 100 ата; г) Р₄= 200 ата.

Р е ш е н и е. Количество тепла, необходимое для нагревания 1 кг воды от 0° С до температуры кипения при заданном постоянном давлении с учетом отклонения изобары от нижней пограничной кривой определяется по формуле

где — энтальпия воды при заданном давлении и при температуре 0° С, равная Apv₀

Используя таблицы водяного пара (приложение 9) и приведенную выше формулу, находим:

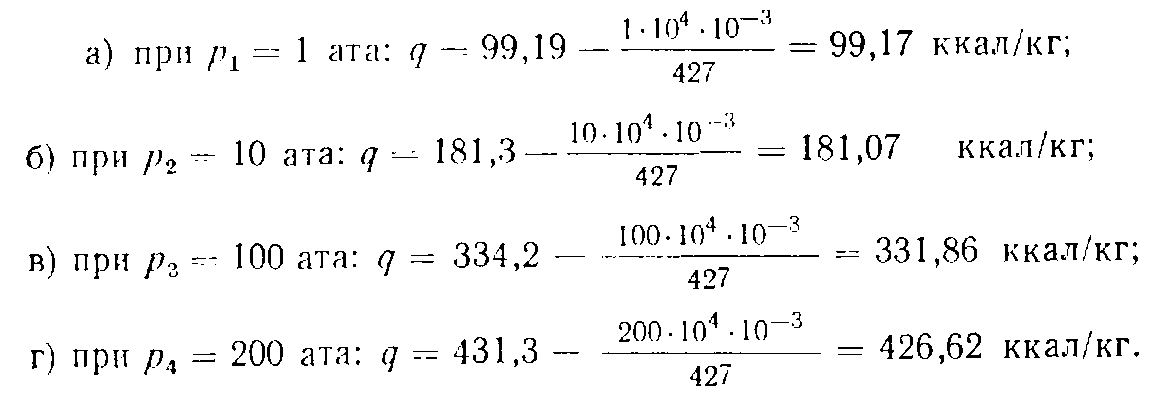
Из полученных цифр видно, что при невысоких давлениях величина энтальпии i’ мало отличается от теплотыq. Поэтому в области не очень высоких давлений можно не учитывать отклонения изобары от нижней пограничной кривой.

Пример. В пароперегреватель парового котла поступает пар при давлении 26 ата со степенью сухости х= 0,95 в количестве 4000 кг/ч. Пароперегревателю сообщается тепло в количестве 600000 ккал/час. Определить температуру перегрева пара.

Р е ш е н и е. Для давления р= 26 ата находим i’=230,9 ккал/кг i= 438.5 ккал/кг.

Значение энтальпии пара на входе в пароперегреватель находим по формуле

Превращение энтальпии пара за счет тепла, переданного в пароперегреватель, будет равно

Энтальпия пара на выходе из пароперегревателя

По таблицам перегретого пара (приложение 10) по значению энтальпии i=797,5 ккал/кг и давлению р=26 ата находим температуру перегретого пара:t= 445° С.

Пример. По двум паропроводам к камере смешения подается перегретый пар при давлении 10 ата в температуре 470° С и влажный пар при давлении 42 ата и степени сухости 0,98. Давление пара после камеры смешения равно 40 ата, а температура 420° С. Часовой расход перегретого пара 3600 кг/час. Определить, сколько подается влажного пара в камеру смешения.

Р е ш е н и е. По таблицам перегретого пара для Р₁= 40 ата иt₁= 470° С находим: i₁= 807 ккал/кг. Из приложения 9 для давления р₂= 42 ата находим: i’ = 261,8 ккал/кг;r=407.0 ккал/кг. По этим данным определяем энтальпию влажного пара

Энтальпию перегретого пара после смешения при Р₁= 40 ата иt₁= 420° С находим по приложению 10: i= 779,1 ккал/кг

Расход влажного пара определим из балансового уравнения

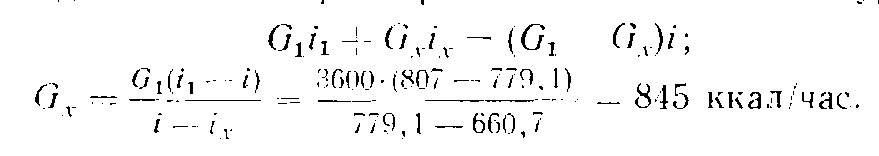
Пример. Начальное состояние пара характеризуется параметрами: р₁=10 ата; х=0,3. Какое количество тепла необходимо подвести к пару при постоянном объеме, чтобы температура пара возросла до 300° С? Определить остальные параметры пара в конечном состоянии. Представить процесс в рv,Tsи isдиаграммах.

Р е ш е н и е. Используя таблицы водяного пара (приложение 9) находим: t_s=179° С;v’₁=0,198 м³/кг; i’₁== 181,3 ккал/кг;r₁=482,1 ккал/кг

Значение удельного объема в начальном состоянии вычисляем по формуле

Так как процесс происходит при постоянном объеме, то

В конечном состоянии при температуре 300° С пар перегрет, так как v’₂<v₂(v’₂=0,02164 м³/кг). По таблице перегретого пара по температуреt= 300° С иv₂= 0,0602 м³/кг определяем давление и энтальпию пара в конечном состоянии: Р₃= 40 ата;i₂=706,9 ккал/кг.

Количество тепла, подведенного dпроцессе, находим, пользуясь формулой

Значение внутренней энергии пара в начальном состоянии

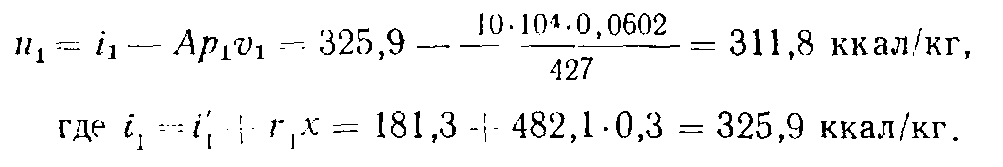
Значение внутренней энергия пара в конечном состоянии

Следовательно

На рис. 41, 42 и 43 процесс показан на диаграммах рv, Тsи is.

Пример. 1 кг водяного пара при постоянном давлении р= 10 ата сжимается от v₁= 0,21 м³/кг доv₂= 0,12 м³/кг Определить состояние пара в начале и в конце процесса, количество отведенного тепла, затраченную работу и изменение внутренней энергии пара. Изобразить процесс в диаграммах рv, Тsи is.

Р е ш е н и е. По таблицам водяного пара находим для р= 10 ата значение v”= 0,1980 м³/кг. Так какv₁>v”, то в начальном состоянии пар перегретый. По таблицам перегретого пара находим температуру и энтальпию пара в начальном состоянии:t₁= 200º С; i₁= 675,4 ккал/кг.

В конечном состоянии v₂<v”, следовательно, пар влажный. Степень сухости пара определяем по формуле

Отведенное тепло определяем по формуле

где

Затраченную работу в процессе определим по формуле

Изменение внутренней энергия пара определяем по формуле

На рис. 44, 45 и 46 процесс показан на диаграммах рv, Тsи is.

Пример. 1 м³пара с начальными параметрами р₁= 12 ата, х= 0,95 изотермически расширяется до 1 ата. Определить количество тепла, сообщенное пару, произведенную им работу и изменение внутренней энергии. Изобразить процесс в диаграммах рv, Тsи is.

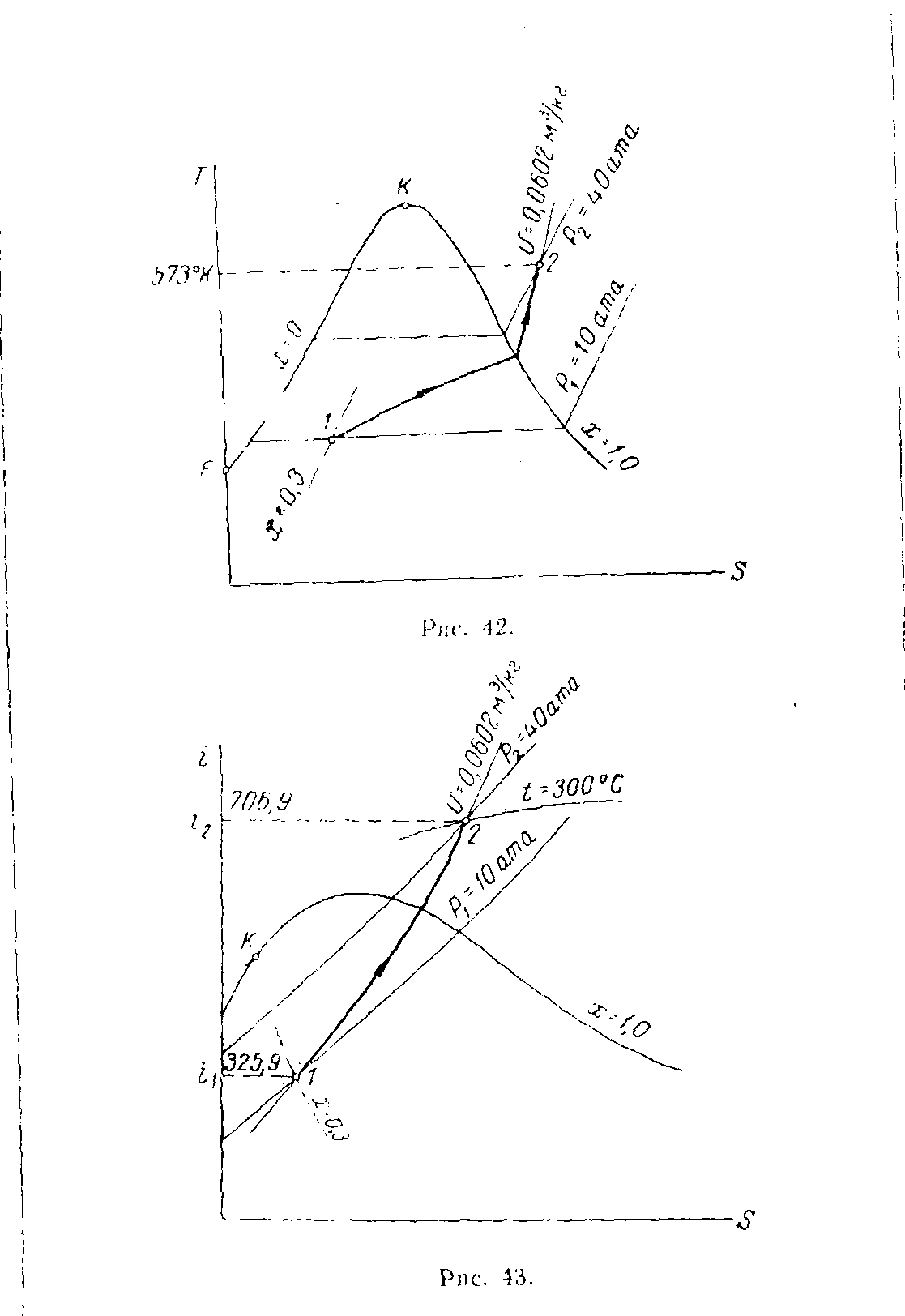
Р е ш е н и е. а) Удельный объем пара в начальном состоянии определяем по формуле:

Весовое количество пара

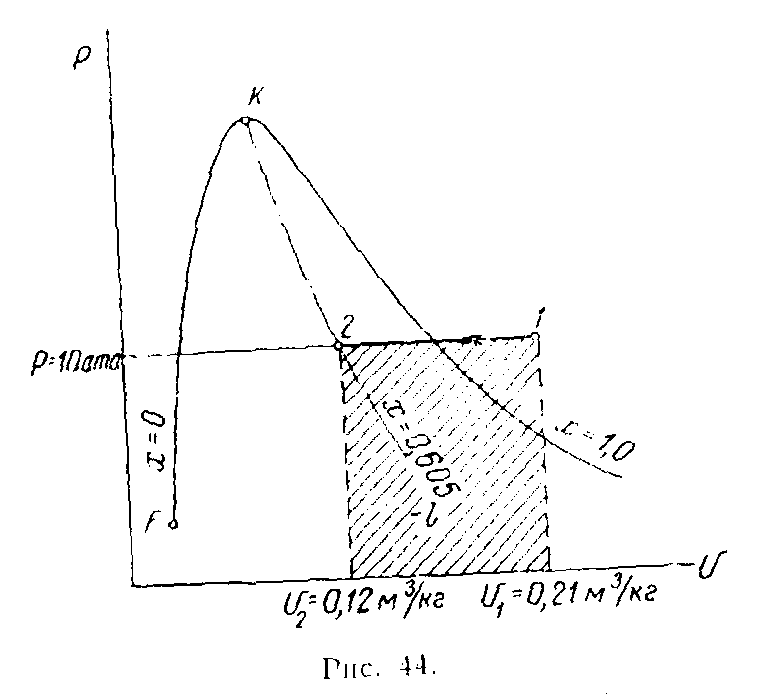
Определяем значения энтальпии, энтропии и внутренней энергии пара в начальном состоянии

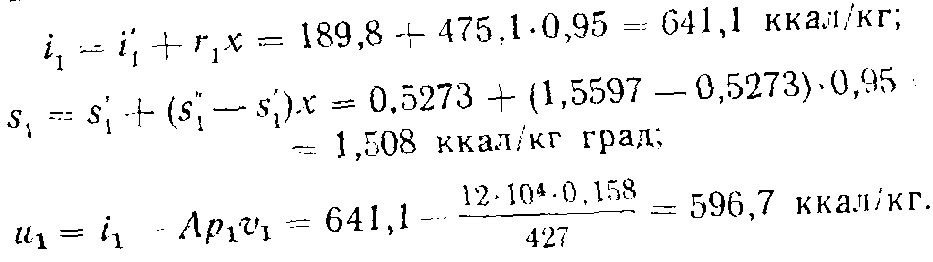
Параметры пара в конце процесса находим по таблицам перегретого пара: v₂= 2,152 м³/кг;i₂= 680,5 ккал/кг;s₂= 1,8586 ккал/кг град.

Количество подведенного тепла

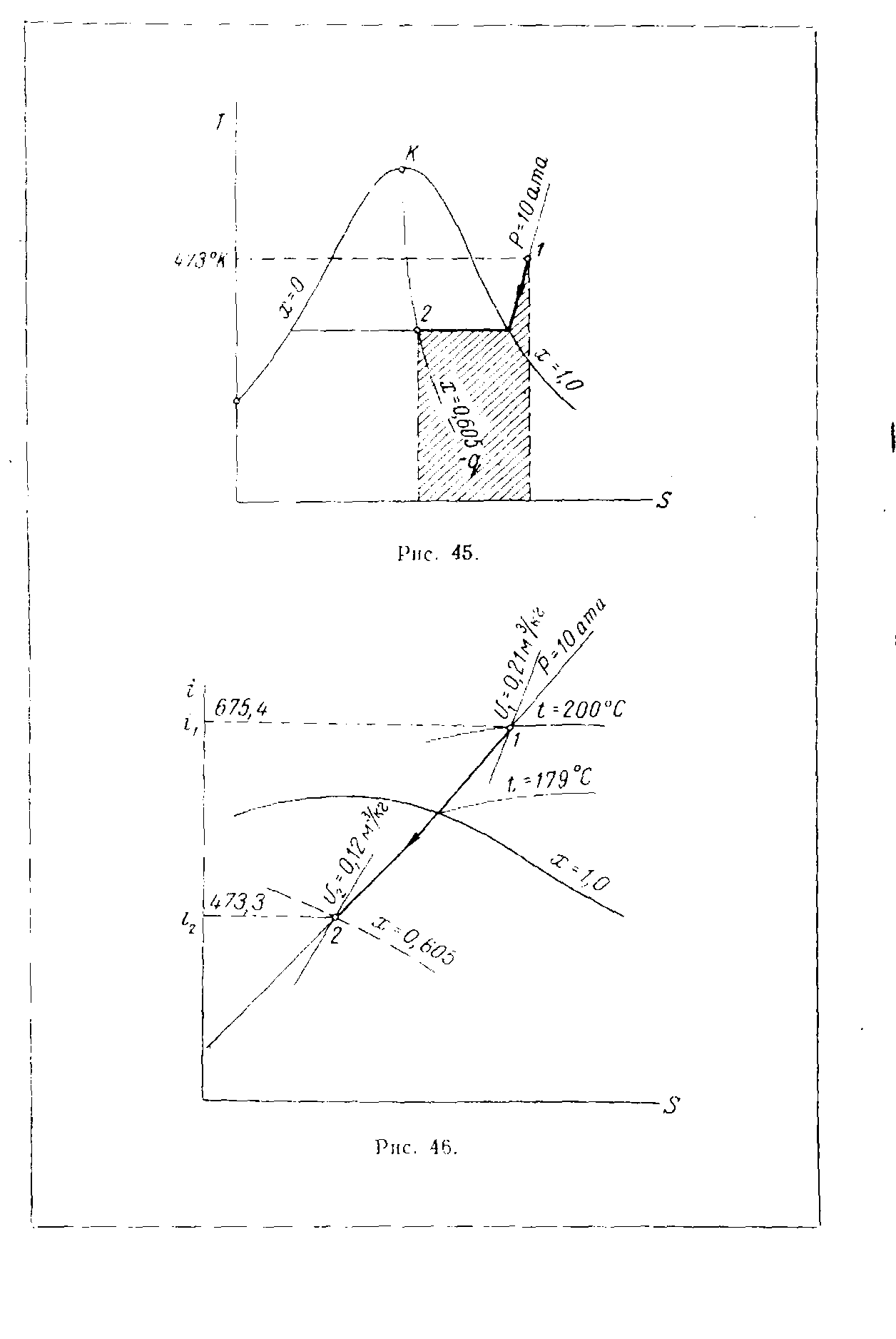
Изменение внутренней энергии

Работа расширения

На рис. 47, 48 и 49 рассмотренный изотермический процесс показан на диаграммах рv, Тsи is.

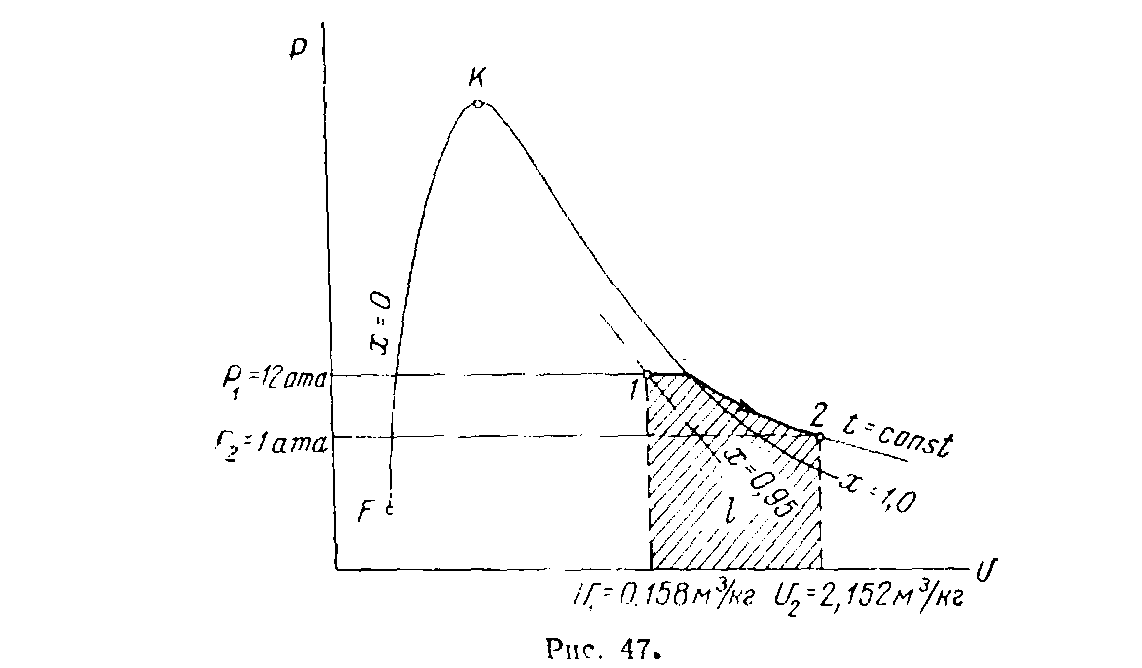
б) Рассматриваемая задача может быть также решена с помощью диаграммы isПоisдиаграмме определяем параметры пара в начальном состоянииv₁= 0,157 м³/кг;i₁= 641,5 ккал/кг;s₁= 1,508 ккал/кг град. Проведя изотерму от начальной точки до пересечения с изобаройp₂= 1 ата, находим параметры пара в конечном состоянии:v2 = 2,15 м³/кг:i2 = 681 ккал/кг:s₂= 1,858 ккал/кг град.

Значения внутренней энергии в начальном и в конечном состояниях находим по формуле

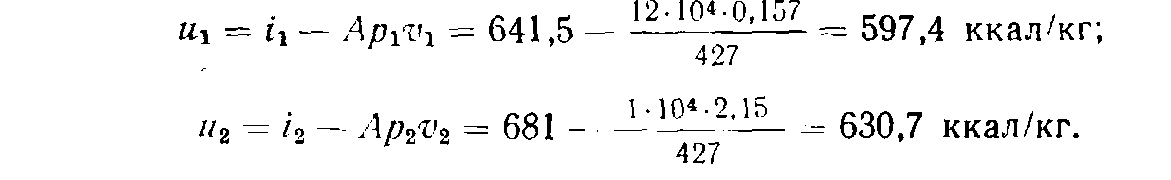
Весовое количество пара, участвующего в процессе

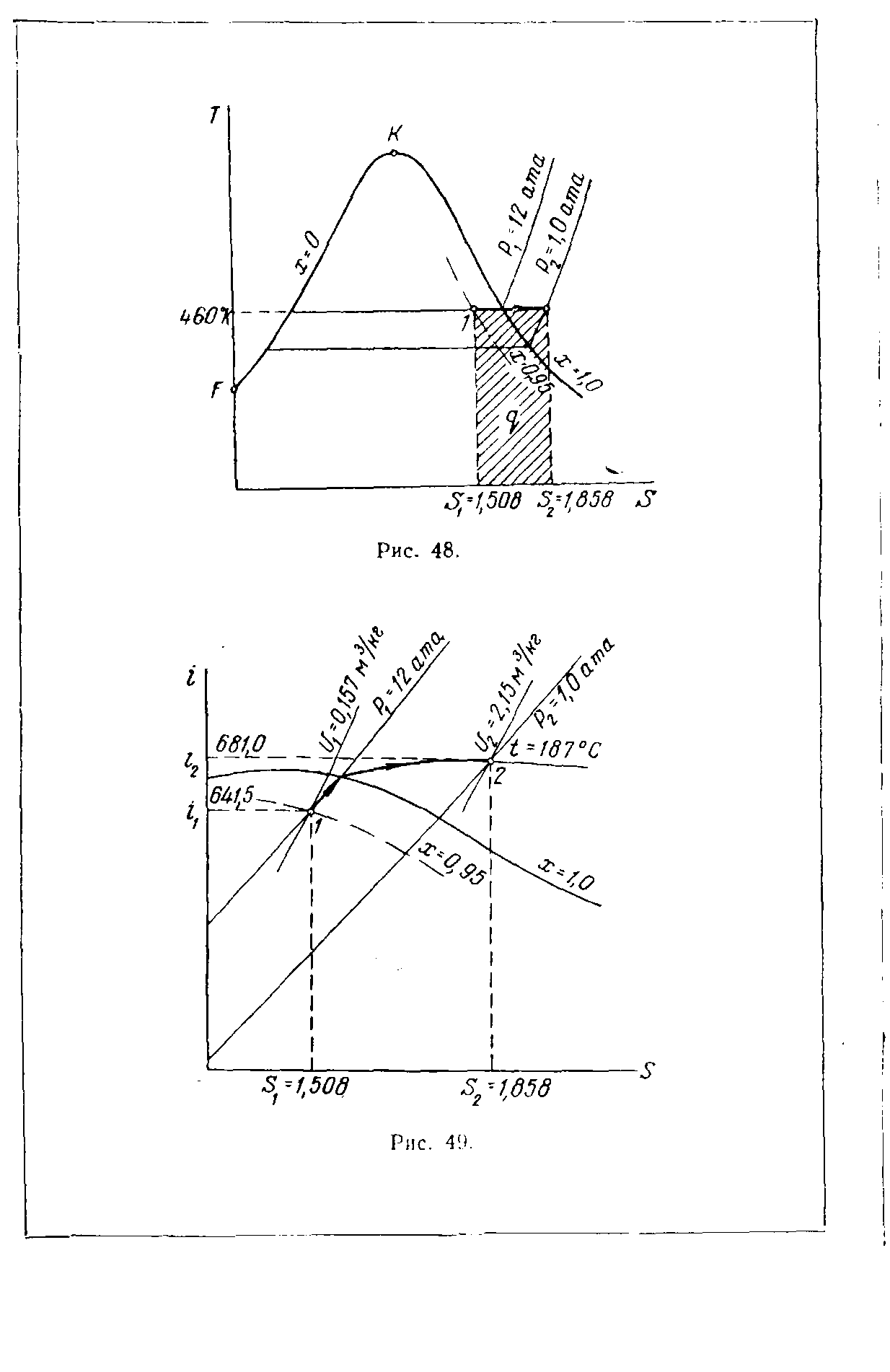
Количество тепла, подведенного к пару

Изменение внутренней энергии

Работа пара в процессе

При сопоставлении результатов расчетов с помощью таблиц и на диаграмме isубеждаемся в их удовлетворительном совпадении.

Пример. 1 кг водяного пара расширяется адиабатно от начальных параметров p₁= 42 ата иt₁= 400° С до давленияp₂= 0,05 ата. Определитьi₁,v₁,i₂,v₂,x₂и работу расширения, используя таблицы водяного пара иisдиаграмму, изобразить процесс на диаграммах рv, Тsиis.

Решение. а) Используя таблицы перегретого пара, определяем параметры в начальном состоянии: v₂= 0,07121 м³/кг:i1 =767 ккал/кг;s₁= 1,6116 ккал/кг град.

В адиабатном процессе s=const, следовательно, степень сухости пара в конечном состоянии определяется из условияs₁=s2.

При p₂-= 0,05 ата по таблицам имеемs₂= 2,0065 ккал/кг град, т. е.s₂>s₁, следовательно, в конечном состоянии пар является влажным.

Значения s₂иs₁находятся по таблице насыщенного пара приp₂= 0,05 ата.

Удельный объем пара в конечном состоянии находим по приближенной формуле

Энтальпия пара i₂

Значения v₂,i₂,r₂определяются по таблицам насыщенного пара приp₂= 0,05 ата.

Определяем значения внутренней энергии пара в начальном и конечном состояниях:

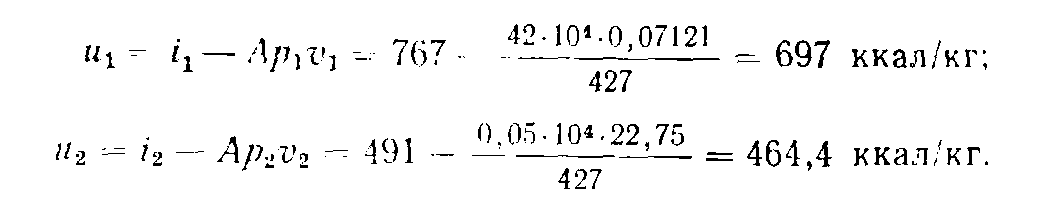
Работу расширения пара находим по формуле

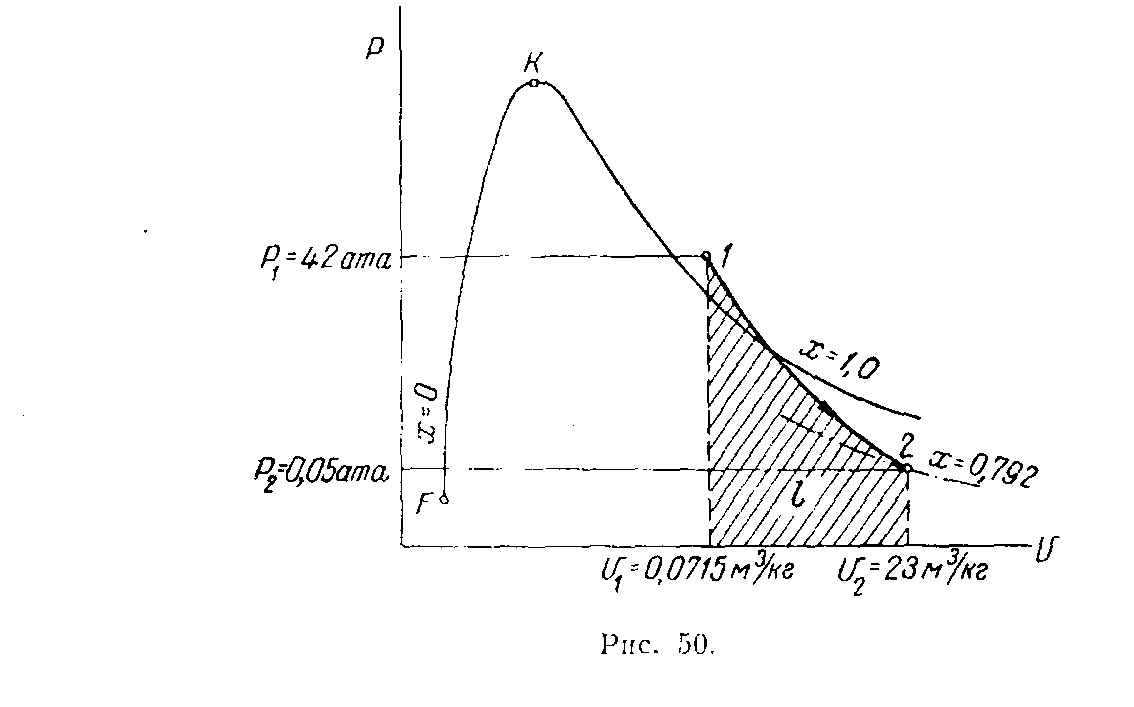
На рис. 50, 51 и 52 рассмотренный адиабатный процесс показан на диаграммах рv,Tsиis.‘

б) Рассматриваемая задача значительно легче и с точностью, достаточной для практических расчетов, может быть решена с помощью isдиаграммы. По isдиаграмме определяем параметры пара в начальном состоянии (рис. 52):v₁= 0,0715 м₃/кг;i1 = 766,5 ккал/кг. Проведя адиабату с начальной точки до пересечения с изобарой р₂= 0,05 ата, находим конечные параметры пара: х₂= 0,792;v2 = 23 м³/кг;i2 = 491 ккал/кг.

Внутренняя энергия в начальном состоянии

внутренняя энергия пара в конечном состоянии

Работа расширения

Пример. Водяной пар при давлении р₁= 25 ата и температуреt₁=300 С дросселируется доp₂= 1,0 ата. Определить температуру пара в конце дросселирования и приращение энтропии.

Решение. Задачу решаем с помощью isдиаграммы. На диаграмме находим точку, характеризуемую параметрамиp₁= 25 ата

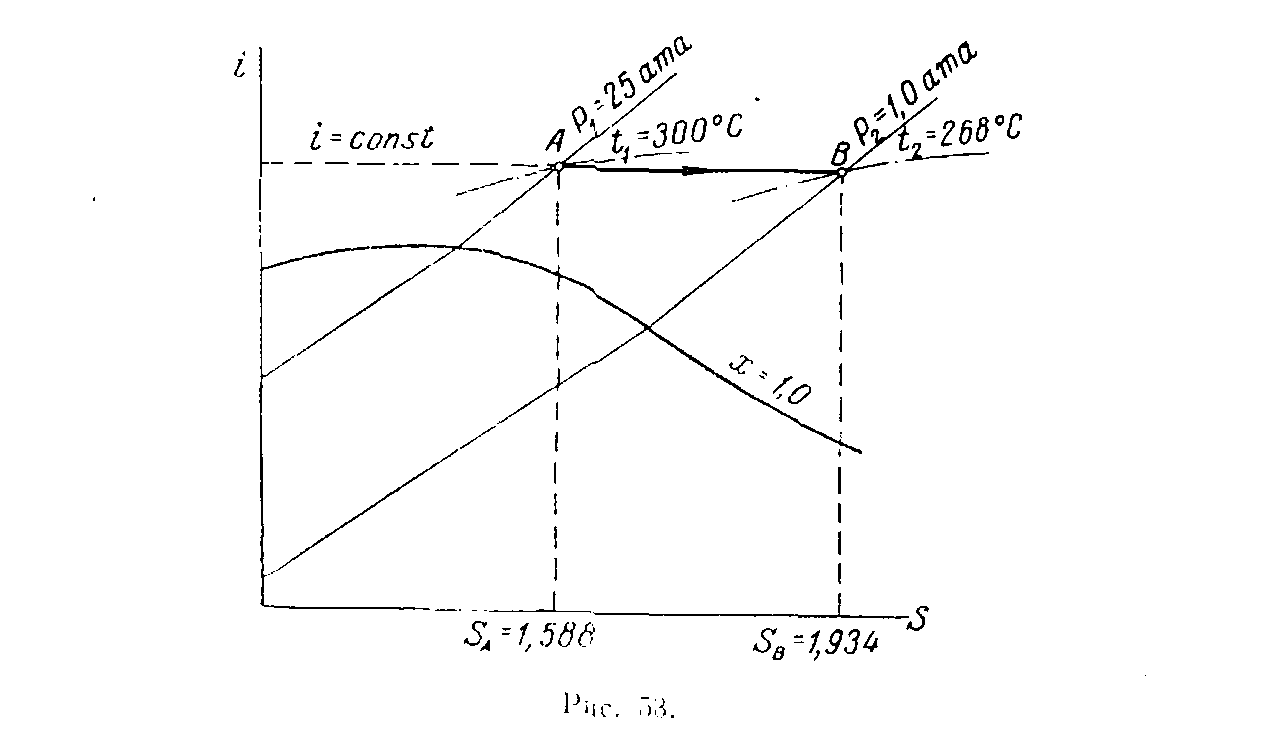
и t₁== 3ОО С (точкаA, рис. 53). Из точки А проводим линию постоянной энтальпии до пересечения с изобарой р₂= 1,0 ата (точка В) и определяем конечную температуру пара:t₂= 268° С.

Приращение энтропии в результате процесса дросселирования составит

Задачи

256. Определить по уравнению Ван дер-Ваальса давление водяного пара для трех состояний: t₁= 250° С иv₁= 0,05096 м³/кг;t₂= 300 С иv₂= 0,128 м³/кг,t₃= 350° С иv₃= 0,2881 м³/кг. Сравнить полученные значения давлений с табличными данными и определить отклонение в процентах.

257. Определить температуру, удельный объем, энтальпию, энтропию и внутреннюю энергию сухого насыщенного пара при давлении 5 ата, используя: а) таблицы водяного пара; б) диаграмму is.

258. Сухой насыщеный пар имеет давление 20 ата. Определить температуру, удельный объем, энтальпию, энтропию и внутреннюю энергию пара, используя: а) таблицы водяного пара; б) диаграмму is

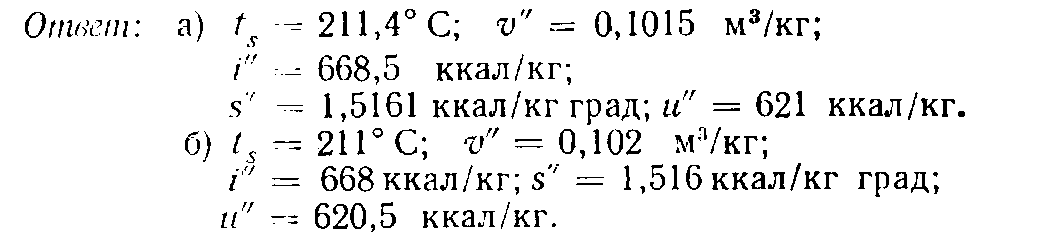
259. Сухой насыщенный пар имеет удельный объем 0,21 м³/кг Определить температуру, давление, энтальпию, энтропию в внутреннюю энергию пара.

260. Термометр, установленный на паропроводе насыщенного пара, показывает температуру 230° С. Показание барометра

755 мм рт. ст. Каково было бы показание манометра на этом паропроводе?

261. Определить давление, объем, энтальпию, энтропию и внутреннюю энергию 3,5 кг сухого насыщенного пара при температуре 250° С.

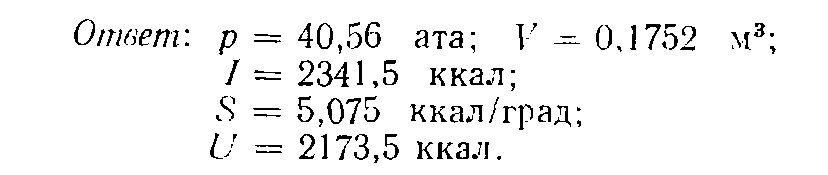
262. Определить температуру, удельный объем, энтальпию энтропию и внутреннюю энергию влажного пара при давлении 28 ата и степени сухости 0.98. используя а) таблицы водяного пара; б) isдиаграмму.

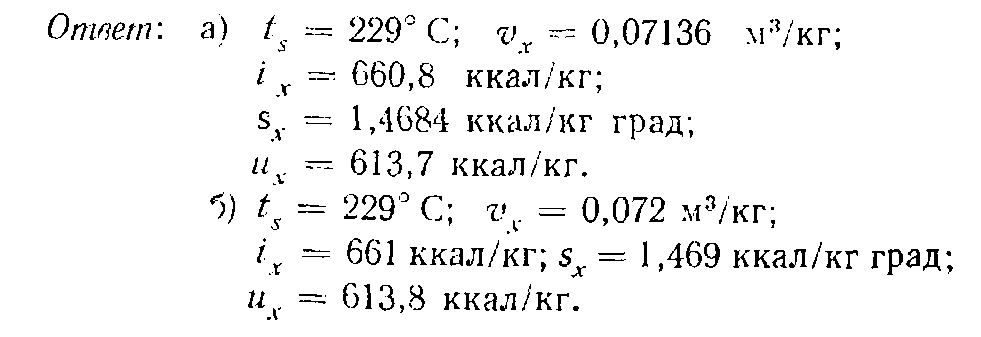
263. Степень сухости влажного пара х = 0,9; температура пара t= 250° С. Определить давление, под которым находится пар, удельный объем, энтальпию, энтропию и внутреннюю энергию а) используя таблицы водяного пара; б) по диаграмме is

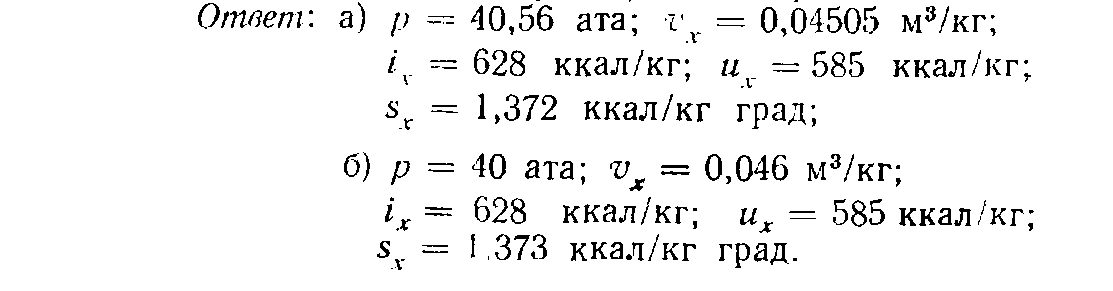
264. Определить степень сухости пара, если: а) 5 кг пара занимают объем 1,1 м³при давлении 8 ата; б) значение энтропии 1 кг пара составляет 1,35 ккал/кг град при давлении 15 ата.

265. до какого давления возможно определение удельного объема влажного пара по приближенной формуле v_x=v“х при степени сухости пара х = 0,95, чтобы ошибка при его вычислении не превышала 1 %?

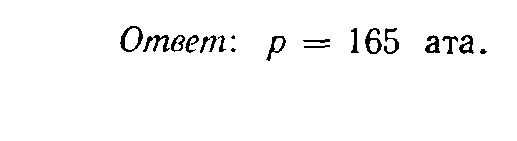266. В ресивер паровой машины (рис. 54) поступает сухой насыщенный пар при давлении 5 ата. Потери тепла в ресивере составляют 4,5%. Какова влажность пара при поступлении его в цилиндр низкого давления (ц. п. д.) паровой машины?

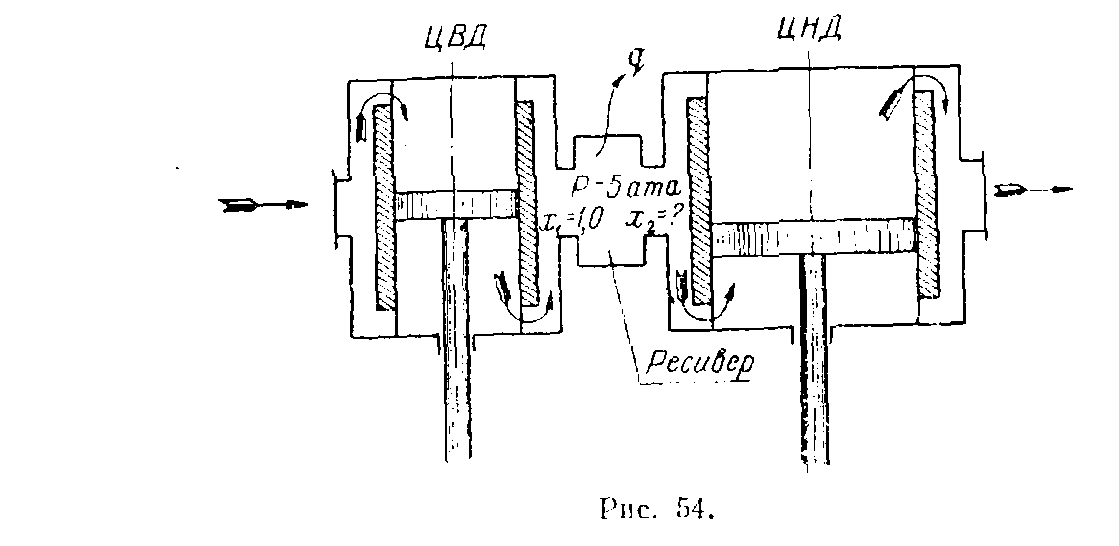
267. Цилиндр объемом 0,4 м³заполнен насыщенным паром Температура пара 160° С, а степень сухости 0,9. Определить весовое количество воды и пара в цилиндре

268. Какой объем занимают 200 кг влажного водяного пара при давлении 16 ата и степени сухости 0,92?

269. Объем парового пространства котла составляет 1,5 м³Определить увеличение веса пара в паровом пространстве, если давление пара возрастает от 16 ата до 20 ата. Степень сухости пара остается неизменной и равной 0,95.

270. Используя таблицы водяного пара, проверить эмпирическую зависимость между удельным объемом и давлением насыщения, выраженную следующим уравнением:

271. Водяной пар имеет следующие параметры: р = 76 ата;

t= 450⁰С. Определить удельный объем, энтальпию, энтропию и внутреннюю энергию пара: а) используя таблицы водяного пара;

б) используя диаграмму is.

Ответ: а) v=0,04131 м³/кг;i= 783,8 ккал/кг;s= 1,5748 ккал/кг град;

u= 710,3 ккал/кг;

б) v= 0,042 м³/кг; i = 783 ккал/кг;s= 1,574 ккал/кг град;

u= 708,3 ккал/кг.

272. Состояние водяного пара характеризуется следующими параметрами: t= 360° С;s= 1,51 ккал/кг град. Определить давление, удельный объем, энтальпию и внутреннюю энергию пара:

а) по таблицам водяного пара; б) по isдиаграмме.

Ответ: а) р = 66 ата; v= 0,03976 м³/кг;i= 730,4 ккал/кг;u= 668,9 ккал /кг;

б) р = 66 ата; v= 0,04 м³/кг;i= 730 ккал/кг;u= 668 ккал/кг.

273. Используя только диаграмму is, определить при давлении

40 ата:

а) параметры сухого насыщенного пара: t_s,v^//, i^//,s^//;

б) теплоту парообразования;

в) энтальпию воды при температуре кипения.

Ответ: а) t= 250° С;v^//= 0,051 м³/кг;i^//= 669 ккал/кг;s“ = 1,45 ккал/кг град;

6) г=410 ккал/кг; в) i’ = 259 ккал/кг.

274. Определить, какое количество тепла необходимо подвести к 2 кг воды при давлении 20 ата и температуре 40° С, чтобы получить:

а) влажный пар со степенью сухости 0,85; 6) сухой насыщенный пар. Показать в диаграмме Тsплощадь, эквивалентную подведенному теплу.

Ответ: а) Q=1120,4 ккал; 6)Q= 1256,2 ккал.

275. Какое количество тепла надо затратить в котле на получение 1 кг пара следующих параметров: р= 28 ата; t= 350° С? Температура питательной воды 100⁰С. Показать в Тsдиаграмме площадь, эквивалентную подведенному теплу.

Ответ: q= 644,6 ккал/кг.

276. Определить значение энтальпии и внутренней энергии воды при температуре кипения при давлении 70 ата и 200 ата. Определить для указанных двух случаев тепло, затраченное на подогрев воды до температуры кипения с учетом отклонения изобары от нижней пограничной кривой. Начальная температура воды 0⁰С.

Ответ: 1) i’=301 ккал/кг; u’=298,8 ккал/кг;q=299,4 ккал/кг;

2) i’= 431,3 ккал/кг;u’=422 ккал/кг;q= 426,6 ккал/кг.

2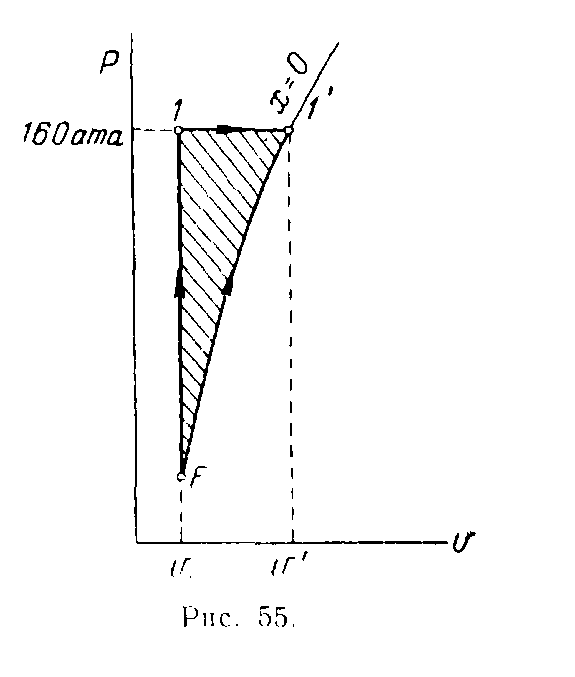77. Определить разность между теплотой жидкости в изобарном процессе 1—1’ и теплом в процессе по нижней пограничной кривойF— 1’ при одинаковом нагреве

жидкости: от 0° С до температуры кипения, соответствующей давлению 160 ата (рис. 55). При решении задачи принять, что изменение удельного объема воды (по нижней пограничной кривой) в зависимости от tsпроисходит по линейному закону. Представить оба процесса в Тsдиаграмме.

Ответ: ∆q= 1,3 ккал/кг.

278. Определить часовой расход угля с теплотворностью 6300 ккал/кг для получения в котле 4000 кг/час пара при р = 16 ата и х=0,98. Коэффициент полезного действия котла 78%. Температура питательной воды 120° С.

Ответ: В= 437 кг/час.

279. В пароперегреватель парового котла поступает пар в количестве 2500 кг/час при давлении 64 ата. Температура пара на выходе из пароперегревателя 500° С. Количество тепла, сообщенное пару в пароперегревателе, 4·10⁵ккал/час. Определить влажность пара на входе в пароперегреватель.

Ответ: х =0,98.

280. Определить часовой расход пара на подогрев 600 кг мазута на 55° С, если начальное давление пара р = 3 ата, а его степень сухости х =0,94. В подогревателе мазута пар конденсируется, и конденсат на выходе из подогревателя имеет температуру 90° С. Теплоемкость мазута 0,5 ккал /кг град.

Ответ: d= 31,2 кг/час.

281.Определить среднюю весовую изобарную теплоемкость водяного пара при 18 ата в интервале температур от 250° до 400° С.

Ответ: _p= 0,543 ккал/кг град.

282. По паропроводу диаметром 80 мм протекает водяной пар с параметрами: р= 28 ата и t=380° С со скоростью 70 м/сек. Определить падение температуры на 1 пог. м паропровода, если известно, что через изоляцию в окружающую среду теряется

500 ккал/м час тепла. Давление пара по длине паропровода можно считать постоянным.

Ответ: ∆ t= 0,076⁰С.

283. Перегретый пар при давлении 22 ата и температуре 375° С смешивается с влажным паром того же давления и превращается в сухой насыщенный. Соотношение между весовыми количествами перегретого и влажного пара 1 : 1,5. Определить начальную степень сухости влажного пара.

Ответ: х= 0,86.

284. Сосуд, содержащий 1 кг пара при давлении 5 ата, сообщается с другим сосудом такого же объема и содержащим 1 кг влажного пара при давлении 2 ата и степени сухости 0,75. Определить состояние пара после смещения.

Указание: давление пара после смещения определить графически.

Ответ: р = 2,8 ата; t= 140° С.

285. Для регулирования температуры перегретого пара иногда примешивают к нему насыщенный пар или впрыскивают в него воду. Определить, сколько надо прибавить насыщенного пара или впрыснуть воды на 1 кг перегретого пара, имеющего давление 64 ата и температуру 550° С, чтобы температура пара при том же давлении составляла 500° С. Давление насыщенного пара или впрыскиваемой воды также равно 64 ата, а температура впрыскиваемой воды 70° С.

Ответ: d_n = 0,187 кг/кг;g_n=0,0375 кг/кг.

286. По двум трубопроводам к месту смешения подается G₁=1500 кг/час перегретого пара при давлении р₁= 16 ата и температуреt₁=300° С иG₂= 2500 кг/час влажного пара при давлении р₂= 12 ата и степени сухости х = 0,95. Определить состояние пара после смешения, если давление его после смешения 12 ата.

Ответ: Пар перегретый, t= 200° С.

287. Построить в диаграмме Тsс соблюдением масштаба изохору в области влажного пара. Начальное давление 15 ата. Начальное состояние пара -сухой насыщенный.

288. К влажному пару при давлении р₁= 12 ата и степени сухости х₁= 0,7 подводится тепло при постоянном объеме. Определить количество тепла, которое необходимо сообщить 1 кг пара, чтобы повысить его степень сухости до 0,95. Каково давление пара в конечном состояния? Представить процесс в рv, Тsиisдиаграммах.

Ответ: р₂= 16,5 ата;q=109,5 ккал/кг.

289. В котле, имеющем пароводяной объем 6 м³, содержится

4500 кг воды и пара при давлении 2 ата. Определить время повышения давления в котле до 28 ата, если от котла пар не отводится и из топки поступает тепло в количестве 20000 ккал/мин.

Ответ: t= 26,2 мин.

290. Начальные параметры водяного пара: p₁ = 45 ата и

t₁= 400° С. Какое количество тепла необходимо отвести от 1 кг пара при постоянном объеме, чтобы превратить его в сухой насыщенный? Представить процесс в рv, Тsи isдиаграммах.

Ответ: q=-74 ккал/кг.

291. В котле объемом 2,5 м³находится пароводяная смесь при давлении 5 ата и степени сухости 0,005. Какое количество топлива необходимо сжечь, чтобы давление повысилось до 14 ата, при условии, что пар из котла не отводится? Теплота сгорания топлива

4500 ккал/кг. К. п. д. котла 69%. Ответ: В’ = 13 кг.

292. 2 кг водяного пара занимают объем 0,2 м³при давлении

10 ата. К пару при постоянном объеме подводится 240 ккал тепла. Определить параметры пара в конечном состоянии. Представить процесс в рv, Тsи isдиаграммах.

Ответ: р₂= 15,4 ата; х₂=0,764.

293. Определить, какое нужно принять давление воды на нижней пограничной кривой, чтобы в результате изохорного отвода тепла получить пар со степенью сухости 0,01 при давлении 40 ата. Определить также количество отведенного тепла в этом процессе. Представить процесс в рv, Тsи isдиаграммах.

Ответ: р = 169,5 ата; q= -132,2 ккал/кг.

294. В трубчатом водоподогревателе осуществляется ‚ изобарный

подогрев воды отработавшим паром от вспомогательных механизмов. Количество тепла, переданного от 1 кг пара к воде, составляет 370 ккал/кг. Температура конденсата греющего пара t_s= 134° С. Определить начальные параметры пара.

Ответ: p₁= 3,1 ата; х₁= 0,715.

295. Определить количество тепла, которое необходимо изобарно подвести к воде с температурой 30° С, чтобы получить 2,1 м³

пара с параметрами р = 6 ата и t=200° С.

Ответ: Q=3800 ккал.

296. 0,5 кг водяного пара при давлении 6 ата занимают объем

0,1 м³. Определить степень сухости пара после подвода к нему

80 ккал тепла при постоянном давлении. Определить внешнюю работу, совершаемую паром, и изменение внутренней энергии. Представить процесс в рv, Тsи isдиаграммах.

Ответ: х₂=0,782;L=1540 кгм; ∆U= 36,3 ккал.

297. В пароохладитель парового котла, расположенный в верхнем барабане, поступает пар при давлении 28 ата и температуре 400° С. От 1 кг пара изобарно отводится 100 ккал тепла. Определить состояние пара на выходе из пароохладителя.

Ответ: t= 233° С;v= 0,074 м³/кг.

298. В пароперегреватель парового котла поступает водяной пар при давлении 16 ата и степени сухости 0,97. Температура пара после пароперегревателя 360° С. Определить работу расширения, количество подведённого тепла и изменение внутренней энергии пара. Представить процесс в рv, Тsи isдиаграммах.

Ответ: l= 9400 кгм/кг;q= 103,3 ккал/кг; ∆u= 81,1 ккал/кг.

299. В цилиндре с подвижным поршнем объемом 0,4 м³находится

2 кг водяного пара при давлении 4 ата. В результате подвода тепла объем пара увеличился в 2 раза. Определить начальные и конечные параметры пара, работу расширения и тепло, участвующее в процессе. Представить процесс в рv, Тsи isдиаграммах.

Ответ: х₁= 0,422; х₂= 0,85;L= 16 000 кгм;Q= 436 ккал.

300. Видимой испарительностью топлива называется количество кг пара, получаемое в данной котельной установке при сжигании 1 кг топлива. Определить видимую испарительность топлива в котельной установке с к.п.д. 0,8, если давление пара в котле 46 ата, температура перегретого пара 450° С. Температура питательной воды 120° С. Теплота сгорания топлива 7000 ккал/кг.

Ответ: И = 8,3 кг/кг.

301. Построить в координатах рvизотермуt= 400° С для водяного пара в интервале давлений от 1 до 50 ата, считая его идеальным газом. Построить зависимостьvот р при этой же температуре по табличным данным. Объяснить, почему при одинаковыхtи р

v_ид>v_реал.

302. Перегретый водяной пар с начальными параметрами p₁=5 ата;t= 250° С изотермически сжимается до объема, в 2 раза меньше первоначального. Определить конечное состояние, количество тепла, участвующего в процессе, работу сжатия и изменение внутренней энергии. Представить процесс в рv, Тsиisдиаграммах.

Ответ: р₂= 9,8 ата;v₂= 0,2418 м³/кг;q= -41,6 ккал/кг; ∆u=3ккал/кг;l= 16 500 кгм/кг.

303. К 1 кг водяного пара при р₁=10 ата иv₁= 0,18 м³/кг подводится 180 ккал/кг тепла. Определить параметры пара в конце процесса и работу расширения, если тепло подводится: а) изобарно; б)изотермически. Представить оба процесса в рv, Тsи isдиаграммах.

Ответ: а) р₂= 10 ата;t₂= - 440° С;l= 15 210 кгм/кг;

б) р₂=0,8 ата;t₂= -179° С;l= 55 700 кгм/кг.

304. В изотермическом процессе к 1 кг водяного пара подведено

150 ккал тепла. Начальное состояние пара определяется параметрами: р₁= 40 ата;s₁=1,52 ккал/кг град. Определить параметры пара в конце процесса, произведенную работу и изменение внутренней энергии пара. Представить процесс в рv, Тsи isдиаграммах.

Ответ: p₂=5,0 ата;t= 300° С;l=55 940 кгм/кг; ∆u= 19,0 ккал/кг.

305. В результате проведения изотермического процесса пар, начальное состояние которого p₁= 10 ата иt= 200° С, превращается в сухой насыщенный. Определить конечное давление, изменение внутренней энергии и работу пара в рассматриваемом процессе. Представить процесс в рv, Тsи isдиаграммах.

Ответ: р₂=15,85 ата; ∆u= -6,3 ккал/кг;l= -10 400 кгм/кг.

306. 10 кг пара при давлении 25 ата и температуре 320° С изотермически расширяются до объема 2 м³. Определить конечные параметры пара, количество тепла, участвующего в процессе, и работу расширения. Представить процесс в рv, Тsи isдиаграммах.

Ответ: р₂= 13,55 ата;v₂= 0,2 м³/кг;Q=- 453 ккал;L=- 171 600 кгм.

307. 5 кг водяного пара, занимающих при давлении 35 ата объем 0,35 м³, расширяются изотермически до давления 5 ата. Определить температуру пара в конечном состоянии и подведенное тепло. Представить процесс в рv, Тsи isдиаграммах.

Ответ: t=300° С (пар перегрет);Q= 695 ккал.

308. Определить давление в точке пересечения адиабаты с нижней пограничной кривой, если начальные параметры пара: p₁= 0,1 ата и х₁= 0,3. Определить также работу, затраченную на адиабатное сжатие 1 кг пара. Представить процесс в рv, Тsи isдиаграммах.

Ответ: р₂= 49 ата;l= -23 650 кгм/кг.

309. Определить работу взрыва парового котла, имеющего водяной объем 20 м³и паровой объем б м³.Давление пара в котле 15 ата,

степень сухости пара в паровом пространстве 0,97. Взрыв рассматривается как адиабатное расширение пара до давления 1 ата.

Ответ: L= 1366 • 10⁵кгм.

310. 1 м³водяного пара расширяется адиабатно от начальных параметров р₁= 16 ата и х₁= 0,95 до противодавления р₂= 0,1 ата. Определить остальные параметры пара в конце расширения и произведенную паром работу. Представить процесс в рv,Tsи isдиаграммах. Ответ: х₂= 0,743;v₂=11,11 м³/кг;i₂= 470 ккал/кг;L=552 000 кгм.

311. Определить, насколько увеличивается работа адиабатного расширения 1 кг пара при изменении конечного давления с 1 ата до 0,1 ата. Начальные параметры пара: p₁= 16 ата,t₁= 320° С. Представить в диаграмме рvувеличение работы расширения 1 кг

пара. Ответ: ∆l= 29 000 кгм/кг.

312. 1 кг водяного пара адиабатно расширяется до объема, в 10 раз больше первоначального. Начальное состояние пара определяется параметрами: p₁=30 ата;t₁=350° С. Определить работу расширения и конечное состояние пара. Представить процесс в рv, Тsи isдиаграммах.

Ответ: p₂= 1, 9 ата; х₂= 0,926;l= 48 500 кгм/кг.

313. Отработавший в паровой машине пар поступает в конденсатор при давлении 0,16 ата. Расход охлаждающей воды в конденсаторе на 1 кг пара составляет 33,5 кг, причем температура охлаждающей воды возрастает на 13⁰С. Определить начальное давление и степень сухости пара, поступающего в конденсатор, если процесс расширения пара в машине адиабатный и к машине поступает пар со степенью сухости 0,97. Ответ: х₂= 0,77;p₁= 15 ата.

314. 1 кг водяного пара с начальными параметрами p₁= 32 ата иt₁=360⁰С адиабатно расширяется до давленияp₂= 0,2 ата. Определить степень сухости пара в конце процесса и полученную работу. Чему равнялось бы давление и какая была бы получена работа, если бы процесс расширения закончился на верхней пограничной кривой? Ответ: х₂=0,835;l= 77800 кгм/кг;

x^/₂=1,0; р^/₂=6,4 ата; l^/= 29 350 кгм/кг.

315. Адиабатный процесс с водяным паром может быть приближенно описан эмпирическим уравнением рv^k= соnst. Определить значение показателя степениkдля адиабатного процесса расширения пара отp₁= 40 ата иt₁= 400° С доp₂= 10 ата.

Ответ: k= 1,30.

316. Построить зависимость адиабатного перепада тепла:

а) от температуры перегретого пара. Начальное давление пара принять 28 ата; конечное давление 0,05 ата. Значения температур перегретого пара: 250; 350; 450 и 550° С;

б) от давления пара. Температуру перегретого пара принять равной 450° С; конечное давление 0,05 ата. Значения давлений: 16; 28; 64 и 150 ата.

317. Построить линию постоянной энтальпии в координатах рvи Тsс соблюдением масштаба. Начальная точка р₁=15 ата и х₁=0,4.

318. Найти по isдиаграмме адиабатный перепад тепла при расширении пара отp₁=14 ата иt₁= 300°С до давленияp₂ =0,06 ата и конечное состояние пара. Насколько уменьшится перепад тепла, если предварительно пар подвергнуть дросселированию

до 6 ата и каково будет при

э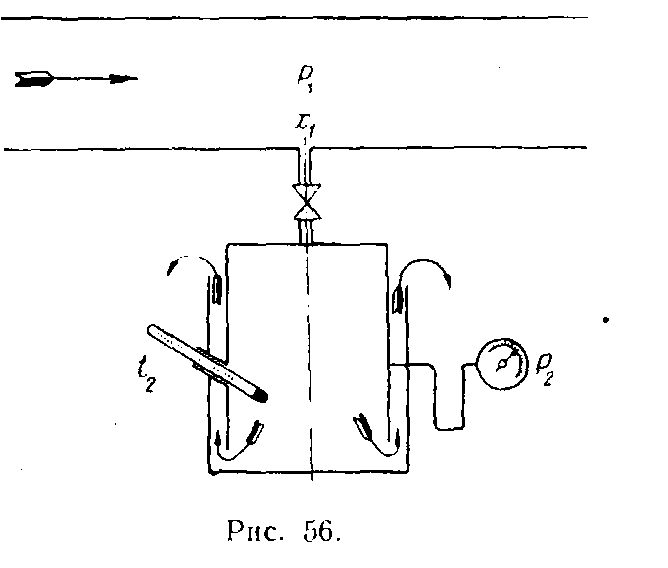том приращение энтропии?

Ответ: х₂= 0,823;

h= 215 ккал/кг; х^/₂= 0,873;

h^/= 186 ккал/кг;

∆s^/=0,092 ккал/кг град.

319. До какого давления

необходимо дросселировать

пар с параметрами р₁=16 ата

и х₁= 0,95, чтобы превратить

его в сухой насыщенный?

Задачу решить с помощью

таблиц водяного пара.

Ответ: p₂= 1,63 ата

320. Процесс дросселирования пара может быть использован для определения степени сухости пара. Для этой цели из паропровода небольшое количество пара отводится в дроссель-калориметр (рис. 56). В дроссель-калориметре измеряется давление и температура пара. Одновременно измеряется давление в паропроводе. Используя полученные данные, определяют степень сухости пара.

Определить степень сухости пара, если давление в паропроводе 15 ата, а в дроссель-калориметре 2 ата и t=130° С. Решить задачу с помощью таблиц водяного пара. Ответ: х = 0,967.

321. Определить потерю работы в адиабатном процессе расширения пара от р₁=16 ата иt₁= 305⁰С доp₂= 0,1 ата, если путем дросселирования давление пара снижено до 5 ата.

Представить процесс расширения пара в рv, Тsи isдиаграммах.

Ответ: ∆l= 16 000 кгм/кг.

322. Водяной пар при давлении 20 ата и степени сухости 0,92 пропускается через редукционный клапан в трубопровод с давлением З ата. Определить остальные параметры пара после дросселирования. Задачу решить с помощью таблиц водяного пара и isдиаграммы. Ответ:x₂=0,964;v₂= 0,595 м³/кг.

Раздел 11

ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ

Процесс истечения упругой жидкости (газ, пар) считается происходящим адиабатно.

Начальные параметры (р₀,v₀,t₀, i₀и т. д.) вытекающей среды принимаются постоянными, не зависящими от расхода, а начальная скорость потокаw₀считается равной нулю (так называемый случай истечения из резервуара бесконечно большой емкости).

Истечение среды происходит в пространство, находящееся под давлением р< р₀. Скорость истеченияwм/сек и секундный весовой расходG_sкг/сек существенно зависят от отношения давлений

=β. Величинаβможет изменяться в пределах от 1 до 0.

Истечение из резервуара осуществляется через сопла или, иначе, насадки. Простое сопло- это короткий конический суживающийся или цилиндрический канал (в частном случае — отверстие в стенке резервуара). Комбинированное сопло или, иначе, сопло Лаваля — это сопло, вначале суживающееся, а затем расширяющееся.

При истечении через простые сопла скорость истечения не может превысить так называемой критической скорости w_кр,равной местной скорости звука, а давление в устье насадки не может быть меньше величины критического давления

Если β>β_кр, то давление в устье (в выходном сечении) равно давлению среды, куда происходит истечение, а скорость истечения на выходе из сопла определяется по формуле

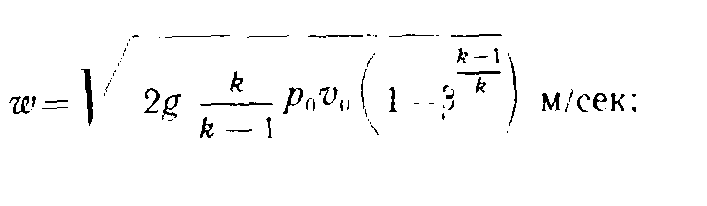
для идеального газа вместо этой зависимости можно использовать формулу

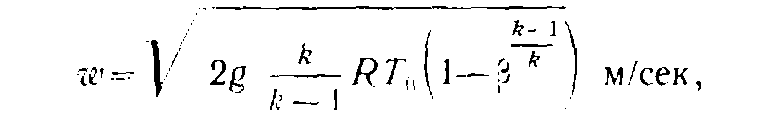
где k- показатель адиабаты.

Секундный расход G_sкг/сек при стационарном режиме истечения определяется по формуле

где wм/сек иvм³/кг — скорость и удельный объем;

fм²— соответствующее сечение (у простых сопел — обычно выходное сечение).

Эта формула может быть приведена к виду

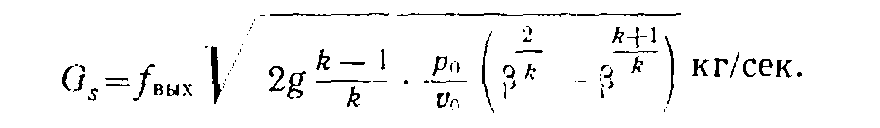
Если β=β_крилиβ<β_кр,то в устье простого сопла устанавливается постоянное давлениеp_кр, и какое-либо уменьшение внешнего давления р не может изменить давления в устье. Поэтому во всех случаях, когдаββ_кр,скорость истечения становится равной критической, а секундный весовой расход достигает максимального значения:

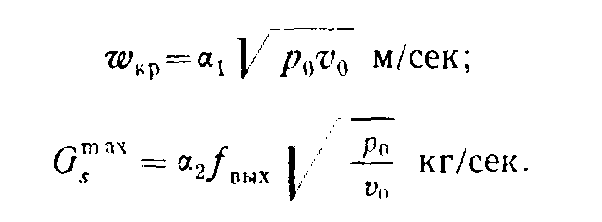
Критические отношения давлений β_кр=, а также коэффициентыα₁иα₂зависят только от показателя адиабатыk(табл. б).

Таблица 6

При малых перепадах давления (обычно измеряемых в мм вод. ст.) можно использовать приближенные формулы

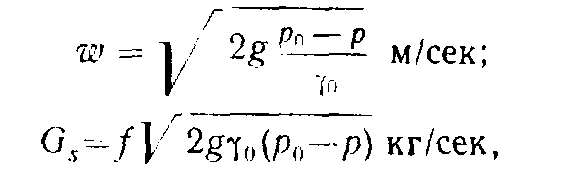
где p₀— р- перепад давлений в мм вод. ст.,Υ₀кг/м³ - удельный вес.

Сопло Лаваля (рис. 57), благодаря комбинации суживающейся и расширяющейся частей, позволяет получить скорость истечения

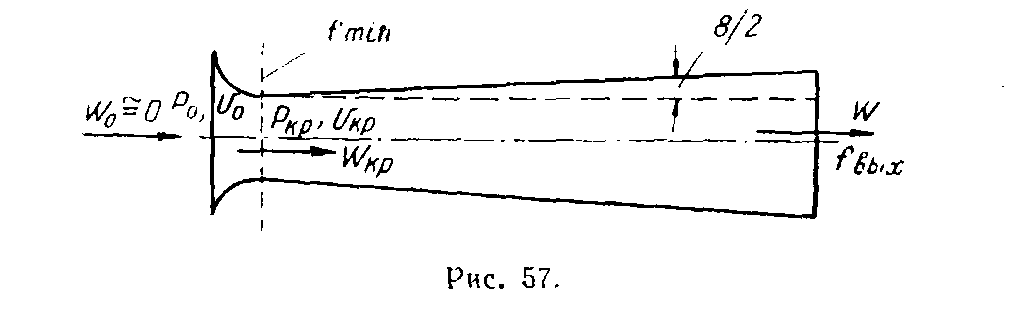
выше критической (сверхзвуковая скорость). Применяется такое сопло только в случае β<β_кр.С помощью сопла Лаваля вся располагаемая потенциальная энергия потока преобразуется в кинетическую энергию.

Весовой секундный расход определяется с заменой f_выхнаf_min -минимальное сечение (в пережиме сопла):

Для сопла Лаваля скорость на выходе w, критическая скоростьw_кри сеченияf_minиf_maxсвязаны друг с другом соотношением

где v_крм³/кг иvм³/кг- удельный объем в минимальном сечении (в котором устанавливается критическое давлениеp_кр) и удельный объем на выходе из сопла. Ввиду адиабатности процесса

Для безотрывного движения струи в расширяющейся части сопла Лаваля угол конусности Υне должен превышать 10—12°.

Приведенные формулы годны для истечения любого рабочего тела. Однако расчет истечения паров обычно производят используя диаграмму is.

Скорость истечения

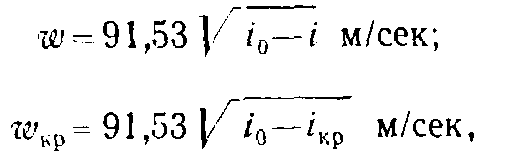
где i_кр— энтальпия пара при давлении р_кр. Для определения энтальпии i иi_крна диаграмме isпроводится адиабата из начальной точки (p₀,t₀или р₀, х₀). Точка пересечения адиабаты с изобарой р

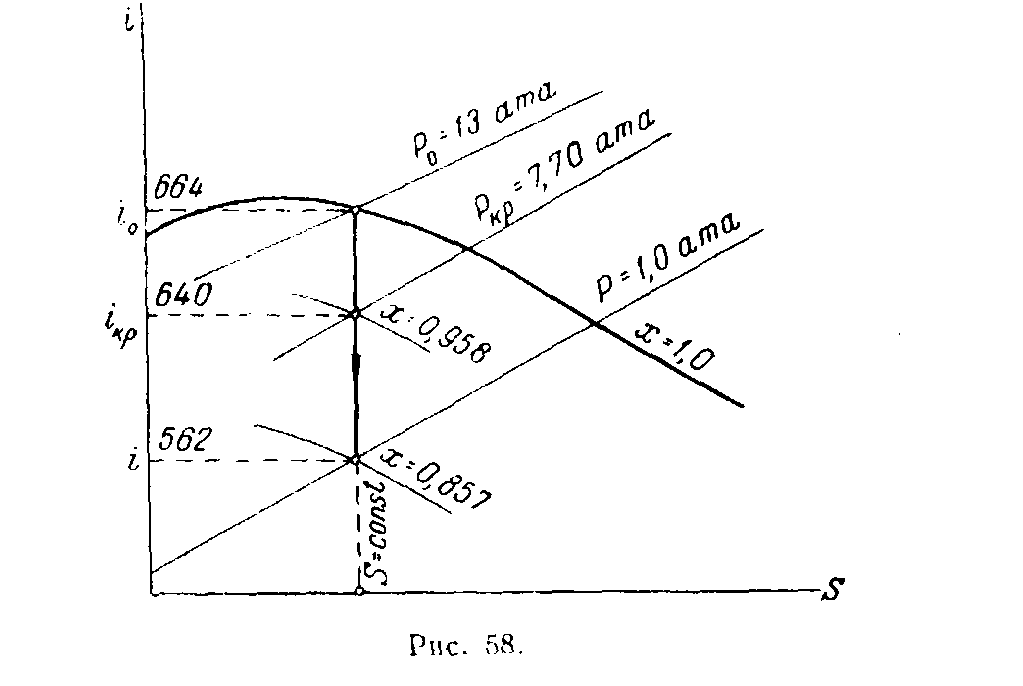
определяет конечное состояние пара и тем самым энтальпию i, а точка пересечения адиабаты с изобарой р_кр=β_крр₀позволяет определить i_кр(рис. 58).

По приведенным формулам может быть определена теоретическая скорость истечения. В реальных условиях часть работы истечения газа или пара затрачивается на преодоление трения, в связи с чем действительная скорость меньше теоретической

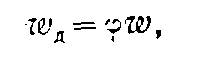
где ψ— так называемый коэффициент скорости:

w- теоретическая скорость истечения.

В связи с необратимостью действительного процесса истечения энтропия должна возрасти (за счет подвода тепла трения) и конечная точка процесса, если его изобразить на диаграмме is(или Тs), будет смещена в область больших значений энтропии.

Конечное состояние процесса адиабатного истечения с трением находится путем следующего построения. Определяется коэффициент потери энергии потока

—

равный отношению потери кинетической энергии потока

к теоретической величине кинетической энергии . Выражая

указанную потерю энергии через энтальпию, получим

где i_д— энтальпия в конце действительного процесса истечения.

Поэтому конечное состояние процесса на диаграмме isнаходится, как точка пересечения изобары р с изоэнтальпой i_д= i +∆ i (рис. 59).

Пример. При истечении воздуха, имеющего давление 4 ата и температуру 37⁰С, в среду с пониженным давлением найти значение р, при котором теоретическая скорость истечения воздуха будет равна критической; определить величину критической скорости.

Решение. Для двухатомных газов β_кр=0,528. Следовательно

р=p_кр= β_крp₀=0,528·4= 2,112 ата.

Критическую скорость найдем из формулы

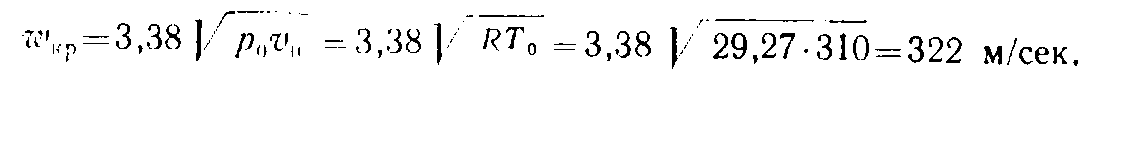
Пример. В кислородном баллоне поддерживается постоянное давление р₀= 60 ата. Газ вытекает в среду с давлением 48 ата через суживающееся сопло. Определить теоретический расход кислорода, если диаметр выходного отверстия сопла 5 мм и начальная температура кислорода 57° С. Определить также расход кислорода при истечении его в атмосферу.

Решение. Для первого случая истечения при β_кр= 0,528 имеем

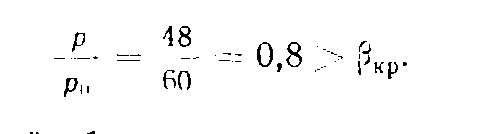
Находим удельный объем

Определяем секундный расход:

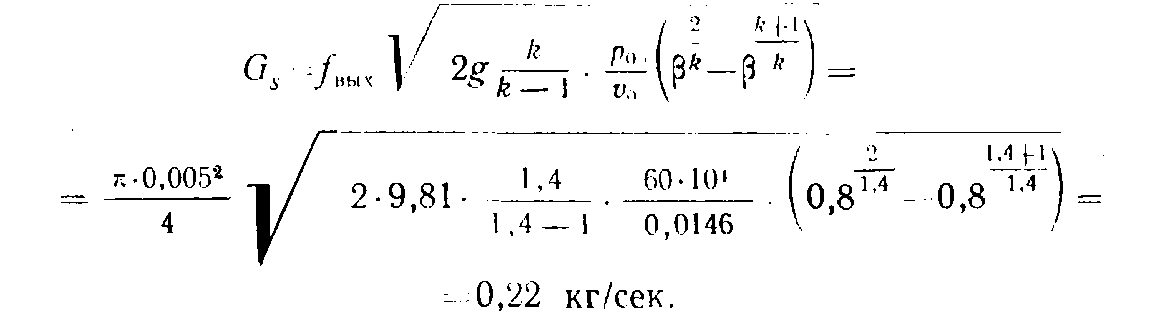
Для второго случая истечения

Определяем секундный расход

Пример. Начальное давление пара р₀= 13 ата. Определить теоретическую скорость истечения насыщенного пара в атмосферу через сопло. Определить, какое необходимо взять сопло, чтобы получить максимальную скорость истечения.

Решение. Так как β=<β_кр=0,577, необходимо применить сопло Лаваля.

Теоретическую скорость истечения найдем, используя диаграмму isдля водяного пара (рис. 58). Проводим адиабату из точки пересечения изобары р₀=13 ата с верхней пограничной кривой до пересечения сечения с изобарой р = 1 ата. Находим: i₀= 664 ккал/кг; i = 562 ккал/кг. Тогда

Определим дополнительно критическую скорость ω_кр.

Находим точку пересечения изобары р_крс адиабатой. В этой точкеi_кр= 640 ккал/кг (х = 0,958). По формуле

Пример. Истечение пара происходит через сопло Лаваля. Начальные параметрыp₀= 18 ата,t₀= 340° С. Противодавление р = = 1 ата. Секундный расходG_s=0,04 кг/сек. Определить действительную скорость истечения и площадь выходного сечения сопла. Коэффициент скоростиψ= 0,94.

Р е ш е н и е. Поскольку β==<β_кр, то действительно необходимо применять сопло Лаваля. Пользуясь диаграммой is(рис. 58), определяем теоретическую скорость истечения по формуле

Действительна я скорость истечения

Коэффициент потери энергии

ξ=1-ξ²=1-0,94²=0,116.

Находим ∆i

Точка, лежащая па пересечении изобары р = 1 ата с изоэнтальпой i_дпоказывает конечное состояние в действительном процессе истечения. Производя указанное построение, определяем параметры пара в выходном сечении:υ= 1,72 м³/кг (х = 0,966).

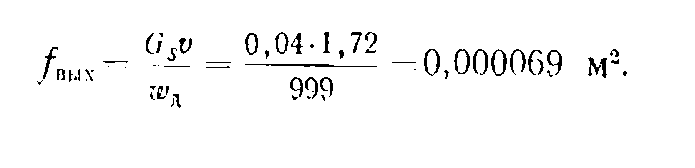
Задачи

323. Определить теоретическую скорость истечения воздуха

и его конечную температуру, если р₀=50 ати, р = 30 ати иt₀== 27° С.

Ответ: ω= 282,4 м/сек;t= -13⁰С.

324. Воздух вытекает через короткое цилиндрическое сопло в атмосферу. Определить критическое давление и теоретическую скорость истечения, если р₀= 9 ата иt₀= 37° С.

Ответ: р_кр= 4,75 ата;ω= 322 м/сек.

325. Определить теоретическую скорость истечения кислорода из баллона в атмосферу, если давление в баллоне р₀= 60 ата, аt₀= 37° С.

Ответ: ω= 306 м/сек.

326. Воздух протекает по трубопроводу, в который вставлено суживающееся сопло. Перед соплом р₀= 26 ата, а за соплом р = 19 ата. Определить скорость истечения и размеры выходного сечения сопла, еслиt₀= 87° С иG_s= З кг/сек.

Ответ: ω249 м/сек;f_max=6,106 см².

327. Кислород под давлением р₀= 56 ата вытекает в среду, имеющую давление р = 34 ата. Начальная температура кислородаt₀= 27° С. Определить теоретическую скорость истечения кислорода, конечную температуру и его расход, если диаметр отверстия, через которое происходит истечение, равен 4 мм.

Ответ: ω= 266 м/сек;t= —12° С;G_s= 0,169 кг/сек.

328. Определить теоретический расход воздуха при истечении его из баллона с давлением 40 ати в атмосферу, если диаметр выходного отверстия З мм и начальная температура воздуха составляет 47° С.

Ответ: G_s= 0,064 кг/сек.

329. Определить теоретическую скорость истечения воздуха в атмосферу (р=1 ата) из камеры, в которой поддерживаются постоянными давление р₀= 1 ати и температураt₀= 370° С.

Ответ: ω= 464 м/сек.

330. Воздух вытекает в атмосферу через сужающееся сопло. Определить теоретическую скорость истечения и давление в устье сопла, если в камере поддерживается давление р₀= 20 ата иt₀= 527° С.

Ответ: ω= 517 м/сек; р — р_кр= 10,56 ата.

331. Газ находится в камере при давлении р₀= 1,8 ата и температуреt₀= 620⁰С. Определить теоретическую скорость и секундный расход газа при истечении его через суживающееся сопло в атмосферу (р = 1 ата). Газовая постояннаяR= 30 кгм/кг град; площадь выходного сеченияf= 9 см²иk= 1,4.

Ответ: ω= 530 м/сек;G_s= 0,212 кг/сек.

332. Определить теоретическую скорость истечения, секундный расход и температуру двухатомного газа на выходе из сопла Лаваля. Давление в камере р₀= 45 ата;t₀= 2000° С; р= 1.2 ата; Р= 30 кгм/кг град;f_min= 120 см².

Ответ: ω=1738 м/сек;G_s= 44,26 кг/сек;t=534°С.

333. Вывести формулу для определения теоретической скорости истечения двухатомного идеального газа в зависимости от начальной температуры Т₀и молекулярного весаμпри условии, чтоβ_кр.

334. Определить теоретическую скорость истечения воздуха из сопла топливной форсунки судового двигателя внутреннего сгорания, если давление сжатого воздуха (распыливающего топливо) р₀= 52 ати, а давление в цилиндре двигателя р= 36 ати. Принять температуру форсуночного воздуха равнойt₀= 37° С

Ответ: ω247 м/сек.

335. Определить теоретическую скорость, с которой протекает воздух через суживающуюся насадку в карбюраторе бензинового двигателя, если разрежение за насадкой составляет 600 мм вод. ст..υ₀= 0,81 м³/кг. Атмосферное давление принять равным 1 ата.

Ответ: ω= 98,9 м/сек.

336. Определить для сопла Лаваля минимальное сечение f_min, выходное сечениеf_вых, длину расширяющейся части сопла, теоретическую скорость и температуру воздуха на выходе, если параметры воздуха на входе в сопло: р₀= 30 ата иt₀= 1827° С; противодавление р = 1 ата;G_s= 106 кг/сек и угол конусностиΥ=12°. Поперечное сечение сопла круглое.

Ответ: f_min = 409 см²;f_вых= 1532 см²;l= 102 см;t=522° С;ω1620 м/сек.

337. Топка судового парового котла работает с разрежением

б мм вод ст. Определить теоретическую скорость и расход воздуха,

поступающего в топку через открытое топочное отверстие размером 200 х 300 мм, если температура воздуха в котельном отделении 42° С и барометрическое давление равно 750 мм рт. ст.

Ответ: ω= 10 32 м/сек;G_s= 0.685 кг/сек.

338. Насыщенный водяной пар давления р₀= 18 ата и степени сухости х₀= 0,96 вытекает через суживающееся сопло в среду, имеющую давление р = 12 ата. Определить теоретическую скорость истечения, состояние пара в конце истечения и часовой расход пара, если площадь выходного сеченияf_вых= 20 мм².

Ответ: ω=383 м/сек;G_s= 182,6 кг/час; х = 0,93;υ= 0,155 м³/кг.

339. Сухой насыщенный пар под давлением р₀= 18 ата вытекает

через сопло Лаваля в среду с давлением р = 2 ата. Определить теоретическую и критическую скорость истечения.

Ответ: ω= 875 м/сек;ω_кр= 458 м/сек.

340. Для условий предыдущей задачи определить размеры сопла, если Υ= 12° иG= 194 кг/час. Поперечное сечение сопла круглое.

Ответ: f_min= 21,2 мм²;f_вых= 48,04 мм²;l= 12,52 мм.

341. Водяной пар при давлении р₀ = 16 ата и температуре

t₀= 400° С вытекает из сопла в среду, имеющую давление р = 1 ата. Определить выходное сечение сопла Лаваля, если расход пара составляетG_s= 1,2 кг/сек.

Ответ: f_вых=1786 мм²;ω=1115 м/сек.

342. Определить теоретическую скорость истечения пара и размеры сопла Лаваля, если начальные параметры пара р₀= 20 ата,t₀=420° С; р = 2 ата;G_s= 1,5 кг/сек иΥ= 12°.

Ответ: ω= 1062 м/сек;f_min= 628 мм²;f_вых=1313 мм².

343. Определить теоретическую скорость истечения и расход пара при истечении его из сопла Лаваля, если начальные параметры пара: р₀= 20 ата иt₀= 350°C; р = 0,5 ата;f_min= 8 см².

Ответ: ω1196 м/сек;G_s=1,96 кг/сек.

344. В паровой турбине через сопло Лаваля вытекает перегретый пар с начальными параметрами р₀= 10 ата иt₀= 350° С. Давление

в конденсаторе 0.1 ата. Коэффициент потери энергии для сопла

ξ= 0,3. Определить отношение площади выходного сечения сопла к этой же площади, рассчитанной для идеального процесса истечения.

Ответ: Площадь выходного сечения действительного сопла больше площади выходного сечения сопла, рассчитанного для идеального процесса, в 1,3 раза.

345. Определить скорость истечения сухого пара в атмосферу, если начальное давление пара р₀= 1,8 ата.

Ответ: ω= 448 м/сек.

346. Определить теоретическую скорость истечения перегретого пара из суживающегося сопла, если начальные параметры пара:

p₀= 14 атм ,t₀= 340° С и р = 0,2 ата.

Ответ: ω= 556 м/сек.

347. Определить теоретическую скорость истечения пара из сопла Лаваля, если начальные параметры пара р₀= 14 атм,t₀= 340° С и р= 0,2 ата. Ответ:ω= 1261 м/сек.

348. Для условий предыдущей задачи определить расход пара через круглое сопло, минимальный диаметр которого d_min= 4 мм.

Ответ: G= 86,1 кг/час.

349. Для условий задачи 346 определить расход пара через круглое сопло, если диаметр выходного сечении d_min= 4 мм.

Ответ: G= 86,1 кг/час.

350. Пар до поступления в сопло Лаваля дросселируется от давления р = 12 ата и х= 0,96 до р₀= 8 ата. Определить расход пара через сопло для случая использования свежего пара и после дросселирования, если истечение пара происходит в среду с давлением 0.2 ата, а площадь минимального сечения сопла составляет 14 мм².

Ответ: G= 94,7 кг/час;G’ = 59 кг/час.

351. Пар с параметрами р₀= 40 ата иt₀= 360° С вытекает через суживающееся сопло в среду с давлением р = 12 ата. Определить теоретическую скорость истечения пара и его параметры в конце расширения. Ответ:ω= 760 м/сек;t= 206° С.

352. Пар с начальными параметрами р₀= 18 ата иt₀= 340° С вытекает через сопло Лаваля в среду с давлением р = 1,6 ата. Определить максимальный удельный расход пара.

Ответ: ()_s^max= 2250 кг/м²сек.