Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2_1-2_136

.doc

Скачиваний:

168

Добавлен:

07.03.2016

Размер:

3.7 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

2.90.

Рис. 2.90

Дано

= 1,8 мм

= 24 10^-3Н/м

= 1 г

= ?

Розв’язок.

Зробимо малюнок.

Крапля відірветься від трубки коли її вага перевищить силу поверхневого натягу, що діє в найменшому по діаметру контуру в місті з’єднання краплі з трубкою.

. (1)

Будемо вважати, що цей діаметр дорівнює діаметру трубки . Тоді з формули коефіцієнта поверхневого натягу можна визначити силу натягу:

, (2)

де — сила поверхневого натягу; — довжина ділянки контуру, що обмежує вільну поверхню.

З виразів (1) і (2) отримуємо рівняння

. (3)

Розв’язуємо рівняння (3) відносно маси однієї краплі

. (3)

Кількість крапель отримаємо з виразу

. (4)

Підставляємо в формулу (4) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

У капілярній трубці радіусом = 0,5 мм рідина піднялася на висоту = 11 мм. Визначити густину цієї рідини, якщо її коефіцієнт поверхневого натягу  = 0,022 Н/м, g = 10 м/с².

2.91.

Рис. 2.91

Дано

= 0,5 мм

= 11 мм

= 22 10^-3Н/м

= ?

Розв’язок.

Зробимо малюнок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

У випадку вгнутої поверхні рідини додатковий тиск р направлений у протилежний від рідини бік і дорівнює:

. (2)

Для поверхні довільної форми:

, (3)

де і — радіуси кривизни двох взаємно перпендикулярних перетинах поверхні рідини.

Цей тиск компенсується тиском стовпа рідини:

. (4)

Тоді висота підняття рідини в капілярних трубках дорівнює

, (5)

де - крайовий кут змочування (в нашому випадку цей кут дорівнює нулю); - густина рідини; - радіус капілярної трубки.

З формули (5) отримаємо вираз для розрахунку густини:

= (6)

Підставляємо в формулу (6) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

Визначить різницю рівнів спирту в двох сполучених капілярах діаметрами = 0,5 мм і = 3 мм? Коефіцієнт поверхневого натягу спирту  = 0,021 Н/м, густина  = 800 кг/м³, g =10 м/с².

2.92.

Рис. 2.92

Дано

= 0,5 мм

= 3 мм

= 21 10^-3Н/м

= 800 кг/м³

= ?

Розв’язок.

Зробимо малюнок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

У випадку вгнутої поверхні рідини додатковий тиск р направлений у протилежний від рідини бік і дорівнює:

. (2)

Для поверхні довільної форми:

, (3)

де і — радіуси кривизни двох взаємно перпендикулярних перетинах поверхні рідини.

Цей тиск компенсується тиском стовпа рідини:

. (4)

Тоді висота підняття рідини в капілярних трубках дорівнює

, (5)

З формули (5) отримаємо вираз для розрахунку різниці висот:

(6)

Підставляємо в формулу (6) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

Знайти масу води, що ввійшла в скляну трубку з діаметром каналу d = 0,8 мм, яка опущена у воду на малу глибину. Вважати змочування повним.

2.93.

Рис. 2.93

Дано

= 0,8 мм

= 73 10^-3Н/м

= 1000 кг/м³

= ?

Розв’язок.

Зробимо малюнок.

Маса води, що ввійшла в скляну трубку дорівнює

. (1)

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (2)

У випадку вгнутої поверхні рідини додатковий тиск р направлений у протилежний від рідини бік і дорівнює:

. (3)

Для поверхні довільної форми:

, (4)

де і — радіуси кривизни двох взаємно перпендикулярних перетинах поверхні рідини.

Цей тиск компенсується тиском стовпа рідини:

. (5)

Тоді висота підняття рідини в капілярних трубках дорівнює

, (6)

З формул (1) і (6) отримаємо вираз для розрахунку маси води:

. (6)

Підставляємо в формулу (6) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

Яку роботу треба здійснити при ізотермічному видуванні мильної бульбашки, щоб збільшити її об'єм від = 8 см³ до V₂=16 см³ ?

2.94.

Дано

= 8 см³

V₂=16 см³

= 0,043 Дж/м²

= ?

Розв’язок.

Додаткова енергія, яку мають молекули в поверхневому шарі рідини, отримала назву поверхневої і визначається таким чином:

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки мильний пузир (хай буде кулею) має зовнішній і внутрішній шар молекул, площа поверхні яких майже рівні, то енергія дорівнюватиме

. (2)

Діаметри бульбашок визначимо через їхні об’єми:

(3)

Звідки отримаємо

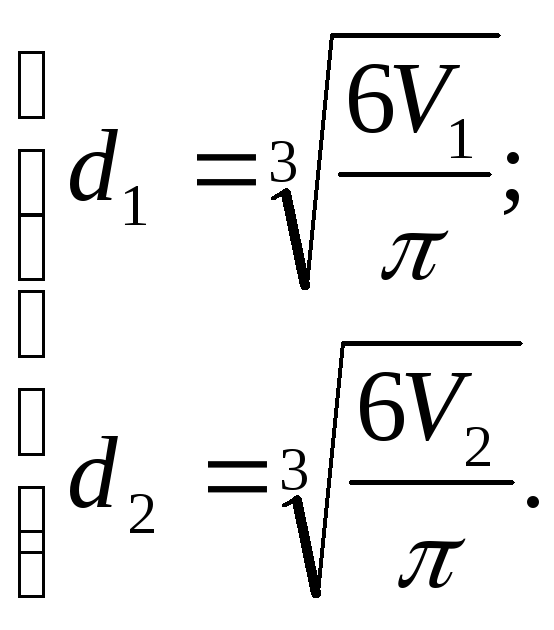(4)

Після підстановки у формулу (2) діаметрів з виразів (4), отримаємо

. (5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

У закритій судині об'ємом V = 0,5 м³ знаходиться  = 0,6 кмоль вуглекислого газу при тиску 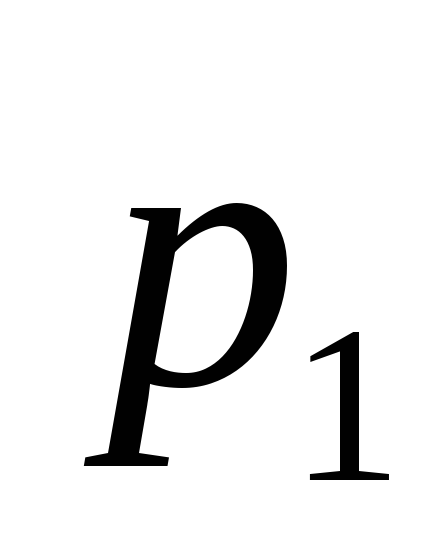= 3 МПа. Користуючись рівнянням Ван-дер-Ваальса знайти, у скільки разів треба збільшити температуру газу, щоб тиск збільшився вдвічі.

2.95.

Дано

= 0,5 м³

 = 0,6 кмоль

= 2

= ?

Розв’язок.

Рівняння Ван-дер-Ваальса для одного молю газу має вигляд

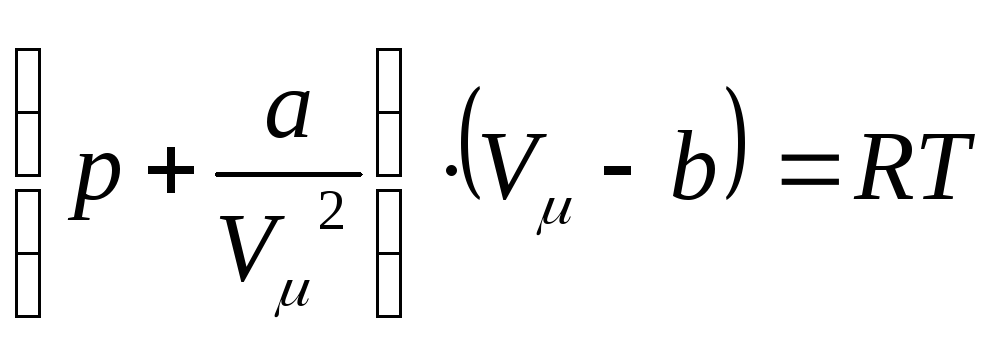, (.1)

а для довільної маси газу

, (2)

де і — сталі Ван-дер-Ваальса. В цьому рівнянні —тиск, зумовлений силами взаємодії молекул, — об'єм, зв'язаний з власним об'ємом молекул.

Зв'язок критичних параметрів — молярного об'єму, тиску і температури газу — із сталими і Ван-дер-Ваальса

. (3)

Сталу знайдемо з другого та квадрату третього рівнянь з (3):

(4)

А сталу визначаємо поділивши одне на одне друге та третє рівняння з (3)

. (5)

Запишемо рівняння (2) для двох станів газу:

(6)

Поділивши друге рівняння системи (6) на перше та урахувавши, що згідно з умовою = 2, отримаємо

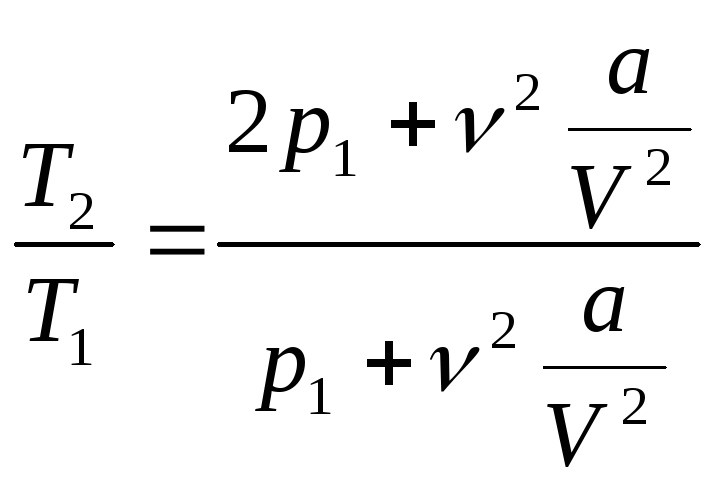. (7)

Підставляємо постійну з виразу (4) у вираз (7) та даних умови і отримаємо відповідь:

Яка енергія виділиться при злитті двох крапель ртуті діаметром d₁= 0,8 мм та d₂= 1,2 мм в одну краплю?

2.96.

Дано

d₁= 0,8 мм

d₂= 1,2 мм

= 0,5 Дж/м²

= ?

Розв’язок.

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки каплі зливаються в одну, то зміна площі поверхневого шару дорівнюватиме

, (2)

де - діаметр великої кулі, який знаходимо з рівності об’ємів великої кулі суми маленьких:

. (3)

Тоді зміну поверхні отримаємо підстановкою (3) у (2):

. (4)

Підставляємо вираз з (4) у формулу енергії (1) і отримаємо вираз для розрахунку енергії:

= (5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

В
192
изначити тиск всередині повітряної бульбашки діаметром d = 4 мм, що знаходиться у воді біля її поверхні.

2.97.

Дано

= 4 мм

= 0,073 Н/м

= 1,013∙10⁶ Па

= ?

Розв’язок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

Тоді повний тиск дорівнюватиме

. (2)

Після підстановки у формулу (2) даних умови задачі, отримаємо відповідь

Гліцерин піднявся в капілярній трубці діаметром каналу d = 1 мм на висоту h = 20 мм. Визначити поверхневий натяг гліцерину. Вважати змочування повним.

2.98.

Рис. 2.98

Дано

= 1 мм

h = 20 мм

= 1260 кг/м³

= 1

= ?

Розв’язок.

Зробимо малюнок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні дорівнює:

. (1)

Цей тиск компенсується тиском стовпа рідини:

. (2)

Порівнявши вирази (1) і (2) отримаємо

. (3)

Підставляємо в формулу (3) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

У воду опущена на дуже малу глибину скляна трубка з діаметром каналу d = 1 мм. Визначити масу води, що ввійшла у трубку.

2.99.

Рис. 2.99

Дано

= 1 мм

= 73 10^-3Н/м

= 1000 кг/м³

= ?

Розв’язок.

Зробимо малюнок.

Маса води, що ввійшла в скляну трубку дорівнює

. (1)

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (2)

Цей тиск компенсується тиском стовпа рідини:

. (3)

Тоді висота підняття рідини в капілярних трубках дорівнює

, (4)

З формул (1) і (4) отримаємо вираз для розрахунку маси води:

. (5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

. Знайти зміну ентропії при ізобарному розширенні = 8 г гелію від об'єму V₁= 10 л до об'єму V₂= 25 л.

2.100.

Дано

= 8 г

= 4∙10^-3 кг/м³

V₁= 10 л

V₂= 25 л

= ?

Розв’язок.

Для любого оборотного кругового процесу, сума зведених кількостей теплоти дорівнює нулю. Тобто:

. (1)

З рівності нулю цього інтеграла слідує, що підінтегральний вираз дорівнює повному диференціалу деякої функції, яка визначається тільки станом термодинамічної системи і не залежить від способу переходу до цього стану. Тобто:

. (2)

Приріст ентропії при переході термодинамічної системи із стану 1 у стан 2

. (3)

Таким чином, зміна ентропії при переході ідеального газу з одного стану у другий, не залежить від виду термодинамічного процесу.

. (4)

З ізобарного термодинамічного процесу:

, (5)

визначаємо відношення температур і змінюємо формулу (4), при цьому використовуючи рівняння Майєра ():

. (4)

Підставляємо в формулу (4) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

Повітряна бульбашка діаметром d = 2,2 мкм знаходиться у воді біля її поверхні. Визначити густину повітря в бульбашці, якщо повітря над поверхнею води знаходиться при нормальних умовах.

2.101.

Дано

= 2,2 мкм