2_1-2_136

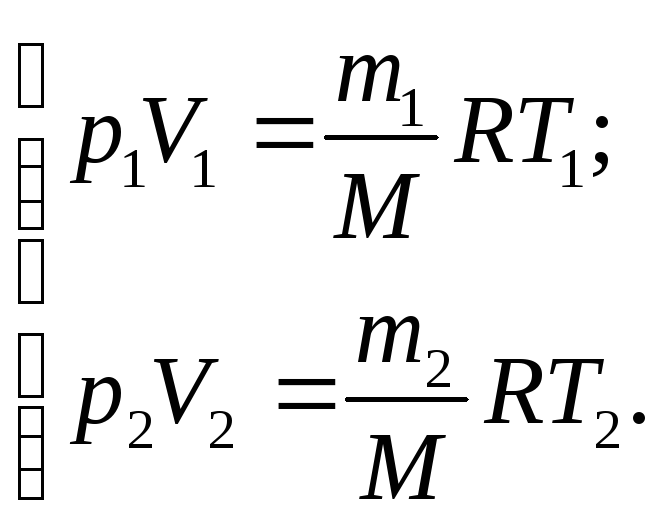(3)

Використаємо умову задачі () тоді система (1) прийме вигляд з якого можна визначити

(4)

Підставляємо отримані відношення з (4) у рівняння системи (2)

(5)

Отримані парціальні тиски з системи (5) в формулу (1) і отримаємо вираз для розрахунку:

= (6)

Підставляємо дані умови в рівняння (6) і отримаємо відповідь:

=

11. Обчислити густину азоту, що знаходиться в балоні під тиском = 2 МПа і що має температуру Т = 400 К.

2.11.

Дано

= 2 МПа Т = 400 К = 28 г/моль

= ?

Розв’язок.

Для розв’язку згадаємо рівняння Клапейрона, в якому В - це газова стала, що має різні значення для різних газів.

= const. (1)

Це ж рівняння для одного молю газу має вигляд:

; (2)

Об’єм довільної маси газу дорівнює:

. (3)

Рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона) записують так

, (4)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Поділимо рівняння на об’єм газу, отримаємо справа густину газу і розв’яжемо це рівняння відносно шуканої величини:

= (5)

Підставляємо дані умови в рівняння (5) і отримаємо відповідь:

=

12. Визначити молярну масу газу, якщо при температурі Т = 154 К і тиску = 2,8 МПа він має густину = 6,1 кг/м³.

2.12.

Дано

= 2,8 МПа Т = 154 К

= ?

Розв’язок.

Для розв’язку згадаємо рівняння Клапейрона, в якому В - це газова стала, що має різні значення для різних газів.

= const. (1)

Це ж рівняння для одного молю газу має вигляд:

; (2)

Об’єм довільної маси газу дорівнює:

. (3)

Рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона) записують так

, (4)

де = 8,31 Дж/(моль∙К) — універсальна газова стала.

Розв’яжемо це рівняння відносно шуканої величини:

= (5)

Підставляємо дані умови в рівняння (5) і отримаємо відповідь:

=

13. Знайти густину  азоту при температурі Т = 400 К і тиску = 2 МПа.

2.13.

Дано

= 2 МПа Т = 400 К = 28 г/моль

= ?

Розв’язок.

Для розв’язку згадаємо рівняння Клапейрона, в якому В - це газова стала, що має різні значення для різних газів.

= const. (1)

Це ж рівняння для одного молю газу має вигляд:

; (2)

Об’єм довільної маси газу дорівнює:

. (3)

Рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона) записують так

, (4)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Поділимо рівняння на об’єм газу, отримаємо справа густину газу і розв’яжемо це рівняння відносно шуканої величини:

= (5)

Підставляємо дані умови в рівняння (5) і отримаємо відповідь:

=

14. У посудині місткістю V = 40 л знаходиться кисень при температурі Т = 300 К. Коли частину газу ізотермічно витратили, тиск в балоні знизився на =100 кПа. Визначити масу витраченого кисню.

2.14.

Дано

= 40 л =100 кПа = 300 К = 32 г/моль

= ?

Розв’язок.

Запишемо рівняння Менделєєва-Клапейрона для двох станів газу:

(1)

Використаємо умову задачі тоді система (1) прийме вигляд

(2)

Віднімаємо від першого рівняння системи (2) друге і отримаємо:

. (3)

З рівняння (3) визначаємо масу витраченого кисню:

. (4)

Підставляємо дані умови в рівняння (4) і отримаємо відповідь:

=

15. Визначити густину водяної пари, що знаходиться під тиском = 2,5 кПа і має температуру Т = 250 К.

2.15.

Дано

= 2,5 кПа Т = 250 К = 18 г/моль

= ?

Розв’язок.

Для розв’язку згадаємо рівняння Клапейрона, в якому В - це газова стала, що має різні значення для різних газів.

= const. (1)

Це ж рівняння для одного молю газу має вигляд:

; (2)

Об’єм довільної маси газу дорівнює:

. (3)

Рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона) записують так

, (4)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Поділимо рівняння на об’єм газу, отримаємо справа густину газу і розв’яжемо це рівняння відносно шуканої величини:

= (5)

Підставляємо дані умови в рівняння (5) і отримаємо відповідь:

=

16. Визначити внутрішню енергію U водню, а також середню кінетичну енергію молекули цього газу при температурі Т = 300 К, якщо кількість речовини цього газу дорівнює = 0,5 моль.

2.16.

Дано

Т = 300 К = 0,5 моль = 2 г/моль = 5

= ? = ?

Розв’язок.

Енергія теплового руху молекул (внутрішня енергія деякої системи, що складається з молекул ідеального газу ( = 6,02∙10²³ моль^-1 – число Авогадро)), тобто одного молю газу, з урахуванням виразу для середньої кінетичної енергія молекули:

, (1)

де і - сумарна кількість ступенів свободи молекули; = 1,38∙10^-23 Дж/К - стала Больцмана; буде дорівнювати:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Для загальної кількості молекул N термодинамічної системи через сталу Авогадро та кількість молів  цього газу N = N_A, вираз (2) записується у наступному вигляді:

. (3)

Підставляємо дані умови в рівняння (3) та (1) і отримаємо відповідь:

= =

17. Визначити сумарну кінетичну енергію Е_к поступального руху всіх молекул газу, що знаходяться в посудині місткістю V = 3 л під тиском = 540 кПа.

2.17.

Дано

V = 3 л = 540 кПа = 3

= ?

Розв’язок.

Сумарна кінетична енергія поступального руху молекул, що складається з молекул ідеального газу ( = 6,02∙10²³ моль^-1 – число Авогадро)), тобто одного молю газу, з урахуванням виразу для середньої кінетичної енергія молекули:

, (1)

де і - сумарна кількість ступенів свободи поступального руху молекули; = 1,38∙10^-23 Дж/К - стала Больцмана; буде дорівнювати:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Для загальної кількості молекул N термодинамічної системи через сталу Авогадро та кількість молів  цього газу N = N_A, і з урахуванням рівняння Менделєєва - Клапейрона, вираз (2) записується у наступному вигляді:

. (3)

Підставляємо дані умови в рівняння (3) і отримаємо відповідь:

=

18. Кількість речовини гелію  = 1,5 моль, температура Т = 120 К. Визначити сумарну кінетичну енергію поступального руху всіх молекул цього газу.

2.18.

Дано

= 1,5 моль Т = 120 К = 3

= ?

Розв’язок.

Сумарна кінетична енергія поступального руху молекул, що складається з молекул ідеального газу ( = 6,02∙10²³ моль^-1 – число Авогадро)), тобто одного молю газу, з урахуванням виразу для середньої кінетичної енергія молекули:

, (1)

де і - сумарна кількість ступенів свободи поступального руху молекули; = 1,38∙10^-23 Дж/К - стала Больцмана; буде дорівнювати:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Для загальної кількості молекул N термодинамічної системи через сталу Авогадро та кількість молів  цього газу N = N_A, і з урахуванням рівняння Менделєєва - Клапейрона, вираз (2) записується у наступному вигляді:

. (3)

Підставляємо дані умови в рівняння (3) і отримаємо відповідь:

=

19. Молярна внутрішня енергія U_m деякого двоатомного газу дорівнює 6,02 кДж/моль. Визначити середню кінетичну енергію обертального руху однієї молекули цього газу. Газ вважати ідеальним.

2.19.

Дано

Um = 6,02 кДж/моль = 5 = 2

= ?

Розв’язок.

Енергія теплового руху молекул (внутрішня енергія деякої системи, що складається з молекул ідеального газу ( = 6,02∙10²³ моль^-1 – число Авогадро)), тобто одного молю газу, з урахуванням виразу для середньої кінетичної енергія молекули:

, (1)

де і - сумарна кількість ступенів свободи молекули; = 1,38∙10^-23 Дж/К - стала Больцмана; буде дорівнювати:

, (2)

Середньої кінетичної енергія обертального руху однієї молекули дорівнює

, (3)

З рівнянь (2) і (3) отримаємо вираз для розрахунку шуканої величини:

, (4)

Підставляємо дані умови в рівняння (4) і отримаємо відповідь:

=

20. Визначити середню квадратичну швидкість молекули газу_, взятого в посудину місткістю V = 2 л під тиском = 200 кПа. Маса газу m = 0,3 г.

2.20.

Дано

V = 2 л = 200 кПа m = 0,3 г

= ?

Розв’язок.

Середня квадратична швидкості молекул дорівнює

. (1)

Використовуємо рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона) для визначення добутку :

, (2)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Зробимо заміну в формулі (1) на отриманий добуток з (2) і отримаємо вираз для розрахунку:

= (3)

Підставляємо дані умови в рівняння (3) і отримаємо відповідь:

=

21. Пів моля водню знаходиться при температурі Т = 300 К. Знайти середню кінетичну енергію обертального руху однієї молекули, а також сумарну кінетичну енергію Е_к усіх молекул цього газу.

2.21.

Дано

Т = 300 К = 0,5 моль = 2 г/моль = 5 = 2

= ? = ?

Розв’язок.

Енергія теплового руху молекул (кінетична енергія деякої системи, що складається з молекул ідеального газу ( = 6,02∙10²³ моль^-1 – число Авогадро), тобто одного молю газу, з урахуванням виразу для середньої кінетичної енергія молекули:

, (1)

де = 2 - сумарна кількість ступенів свободи обертального руху однієї молекули; = 1,38∙10-23 Дж/К - стала Больцмана; буде дорівнювати:

, (2)

де = 5 - сумарна кількість ступенів свободи руху молекули; = 8,31 Дж/(моль∙К) – універсальна газова стала.

Для загальної кількості молекул N термодинамічної системи через сталу Авогадро та кількість молів  цього газу N = N_A, вираз (2) записується у наступному вигляді:

. (3)

Підставляємо дані умови в рівняння (1) та (3) і отримаємо відповідь:

= =

22. При якій температурі середня кінетична енергія поступального руху молекули газу дорівнює = 4,14 10^-21 Дж?

2.22.

Дано

= 4,14 10-21 Дж

= ?

Розв’язок.

Середньої кінетичної енергія молекули:

, (1)

де = 3 - сумарна кількість ступенів свободи поступального руху однієї молекули; = 1,38∙10^-23 Дж/К - стала Больцмана.

Розв’язуємо рівняння (1) відносно температури і отримаємо відповідь:

=

2.23. Визначити молярну масу двоатомного газу і його питому теплоємність, якщо відомо, що різниця питомих теплоємкостей цього газу дорівнює 260 Дж/кг К.

2.23.

Дано

= 5 = 260 Дж/(кг∙К)

= ? = ? = ?

Розв’язок.

Між питомою і молярною теплоємністю існує співвідношення:

(1)

де - молярна маса речовини, моль/кг.

Молярні теплоємкості газу при ізобарному і ізохорному процесі пов’язані рівнянням Майора:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Тоді питомі теплоємності пов’язані таким чином:

. (3)

З рівняння (3) визначаємо молярну масу:

= (4)

Питома теплоємність газу для випадку його участі в ізохорному процесі дорівнює

, (5)

- кількість ступенів вільності молекул газу.

Питома теплоємність газу при ізобарному процесі дорівнює:

. (6)

Підставляємо дані умови в рівняння (4) та визначене значення молярної маси в рівняння (5) та (6) і отримаємо відповідь:

= = =

24. Визначити показник адіабати ідеального газу, який при температурі Т = 350 К і тиску = 0,4 МПа займає об'єм V = 300 л і має теплоємність = 857 Дж/К.

2.24.

Дано

Т = 350 К = 0,4 МПа V = 300 л = 857 Дж/К

= ?

Розв’язок.

Показник адіабати ідеального газу це відношення молярних теплоємкостей до :

. (1)

Теплоємність речовини - це відношення кількості теплоти dQ, що поглинається нею у термодинамічному процесі, до зміни температури dT, що сталася за рахунок надання речовині цієї кількості теплоти:

. (2)

Питомою теплоємністю.

, (3)

Молярною теплоємністю називають кількість теплоти, яка потрібна для підвищення температури одного моля речовини на 1 К.