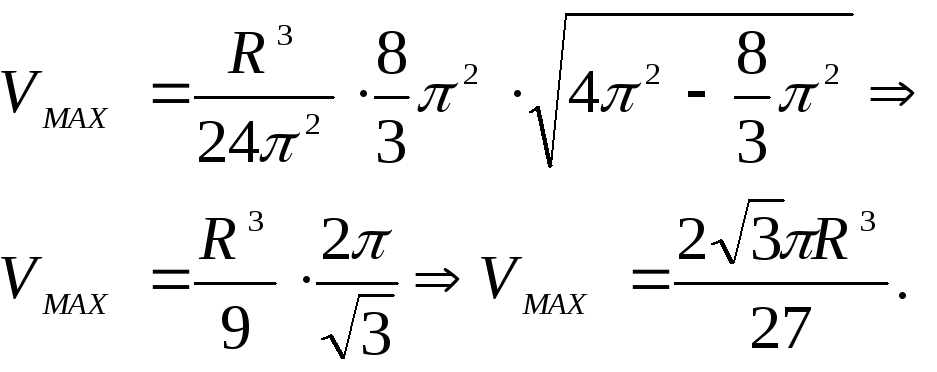- •VI. Теореми про диференційовні функції
- •6.1. Теорема Ролля
- •6.2. Теорема Коші
- •6.3. Теорема Лагранжа
- •6.4. Правило Лопіталя
- •Приклади
- •Розв’язання
- •VII. Дослідження функцій
- •7.1. Зростання і спадання функцій
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язання.
- •Приклади.
- •Розв’язання
- •7.3. Найбільше і найменше значення функції на відрізку
- •Приклади для самостійного розв’язання.
- •7.4. Опуклість і угнутість кривої. Точки перегину
- •Приклади для самостійного розв’язання
- •7.5. Асимптоти графіка функції
- •Приклади для самостійного розв’язання. Знайти асимптоти кривих
- •7.6. Загальна схема дослідження функцій
- •Приклади для самостійного розв’язання
- •Контрольні завдання
- •Вказівки до розв’язування задач
- •До задачі 10
- •До задачі 11
До задачі 10
Варіант 0.
Знайти найбільше і найменше значення функції
![]()
на проміжку [2,6].
Розв’язання.
Знайдемо похідну функції і прирівняємо її до нуля, отримаємо абсциси стаціонарних точок
![]()
Значення х=1 не входить в даний проміжок, а значення функції в
точці х=3 буде
![]()
Знаходимо значення функції на кінцях проміжка:
![]()
![]() .
.
Серед отриманих значень функції
![]()
![]()
![]()
Найменшим
буде![]() а
найбільшим
а
найбільшим![]()
До задачі 11
Варіант 0.
З
бляшаного круга радіуса R
вирізають сектор з центральним кутом
![]() і з нього скручують конічну лійку. При
якому значені кута
і з нього скручують конічну лійку. При
якому значені кута![]() об’єм
лійки буде найбільшим? Знайти його.
об’єм
лійки буде найбільшим? Знайти його.
Р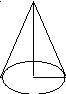 озв’язання.
озв’язання.
 B
B
R R
- сектор
h 0
r - конічна лінійка A
Довжина
кола основи співпадає з довжиною
![]() тобто
тобто
![]()
Об’єм
конуса
![]() .
.
Знайдемо
![]()
![]()
Тоді
![]()
Знаходимо
похідну по
![]()
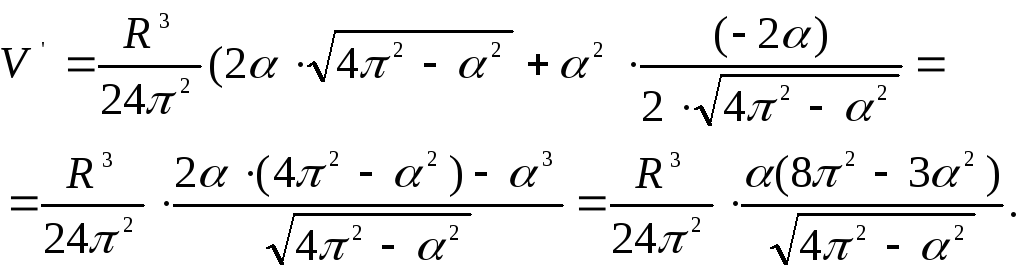
Розв’язуємо
рівняння
![]()
![]()
Крім
того, похідна V’
визначена для
![]() ,
де
,
де
![]()
З начення
начення![]() не підходить, бо вибираємо значення
не підходить, бо вибираємо значення![]()
+ -
0
![]()
![]()
![]() (V’)
(V’)
В
точці
![]() маємо максимум
маємо максимум