
- •VI. Теореми про диференційовні функції
- •6.1. Теорема Ролля
- •6.2. Теорема Коші
- •6.3. Теорема Лагранжа
- •6.4. Правило Лопіталя
- •Приклади
- •Розв’язання
- •VII. Дослідження функцій
- •7.1. Зростання і спадання функцій
- •Розв’язання
- •Розв’язання
- •Приклади для самостійного розв’язання.
- •Приклади.
- •Розв’язання
- •7.3. Найбільше і найменше значення функції на відрізку
- •Приклади для самостійного розв’язання.
- •7.4. Опуклість і угнутість кривої. Точки перегину
- •Приклади для самостійного розв’язання
- •7.5. Асимптоти графіка функції
- •Приклади для самостійного розв’язання. Знайти асимптоти кривих
- •7.6. Загальна схема дослідження функцій
- •Приклади для самостійного розв’язання
- •Контрольні завдання
- •Вказівки до розв’язування задач
- •До задачі 10
- •До задачі 11
Вказівки до розв’язування задач
типового варіанту
До задачі 1
Варіант 0.
![]()
Число
x
= -1 - корінь
чисельника і знаменника. Щоб усунути
невизначеність
![]() необхідно чисельник і знаменник розкласти
на множники. Для квадратного тричлена
відомо, що
необхідно чисельник і знаменник розкласти
на множники. Для квадратного тричлена
відомо, що
![]()
![]()
Многочлен
![]() ділиться на різницю
ділиться на різницю![]()
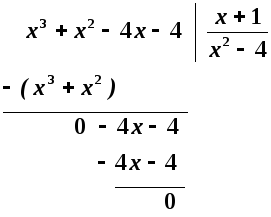
Тому маємо
![]()
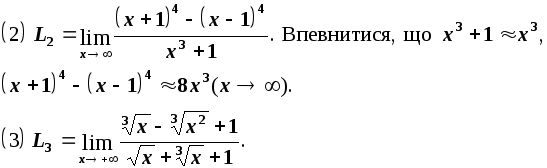
Визначити
старші члени в чисельнику та знаменнику.
Відп.:![]()
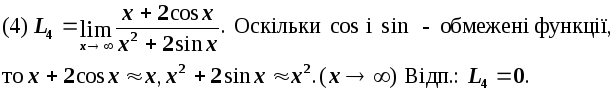
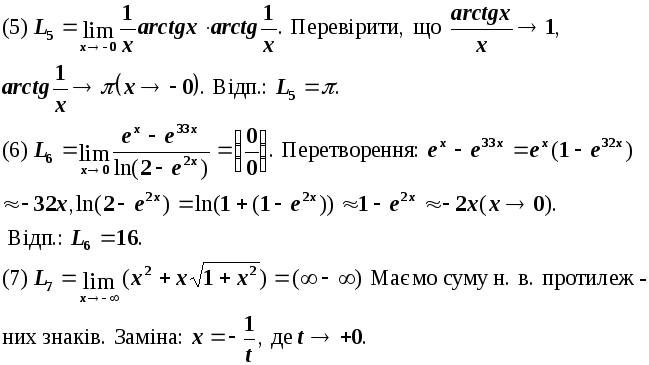
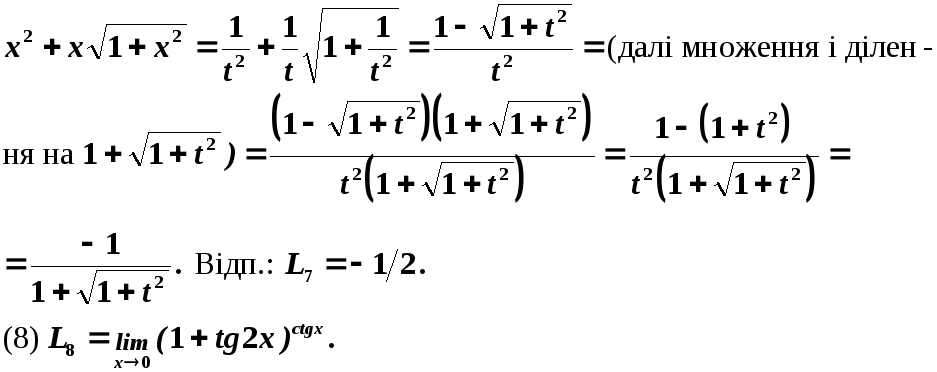 Маємо
невизначеність
Маємо
невизначеність
![]()
Перетворивши
за допомогою тотожності
![]() Далі
необхідно користати- сяеквівалентними
Далі
необхідно користати- сяеквівалентними
![]() Відп.:
Відп.:![]()
До задачі 2
![]()
Розв’язання.
Функція
![]() не існує в точціx0
= -1.Легко
з’ясувати,
що (x
- 2)/(x
+ 1)
— додатня
н. в. при
не існує в точціx0
= -1.Легко
з’ясувати,
що (x
- 2)/(x
+ 1)
— додатня
н. в. при
![]() а
при
а
при![]() — від’ємна
н. в. Тому
— від’ємна
н. в. Тому
![]() Оскільки
f
(x)
неперервна
(при x
< -1
і
при x
> -1)
і
Оскільки
f
(x)
неперервна
(при x
< -1
і
при x
> -1)
і
![]() ,то
,то![]() Ескіз графіка див. нарис.
Ескіз графіка див. нарис.
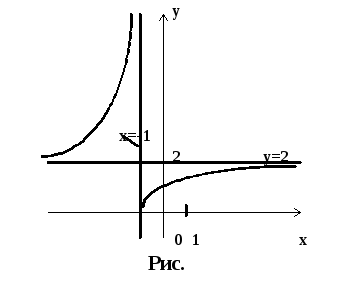
До задачі 3.
Варіант 0.
![]()
Розв’язання.Похідною алгебраїчної суми функцій є алгебраїчна сума похідних, тобто:
![]()
Використовуючи правило диференціювання добутку двох функцій та формули знаходимо:
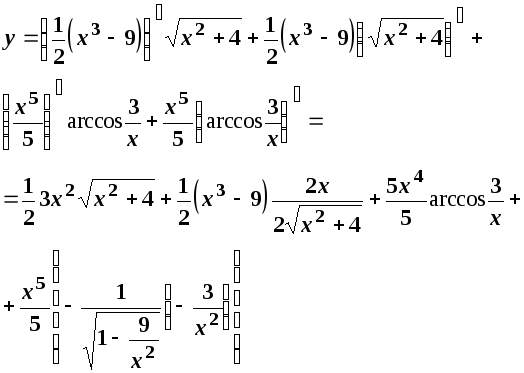
Після скорочення і розкриття дужок остаточно отримуємо:
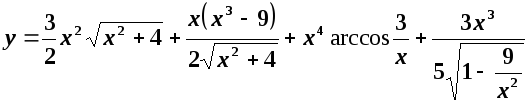
2.![]()
Розв’язання.За правилом диференціювання маємо:
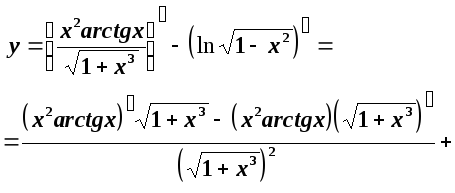
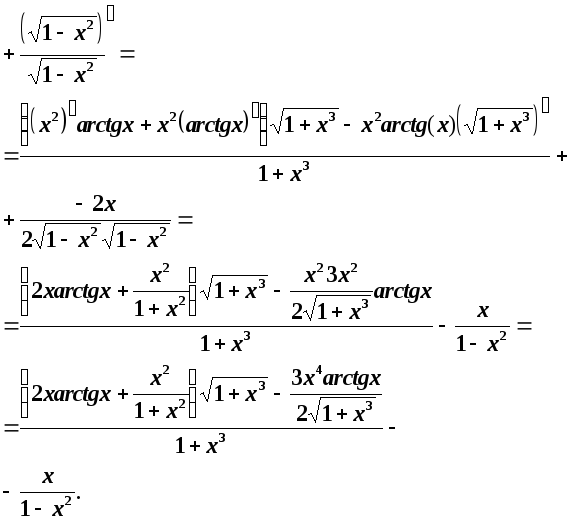
3.![]()
Розв’язання.Для знаходження похідної скористуємось правилом логарифмічного диференціювання.
Спочатку прологарифмуємо функцію за натуральним логарифмом:
![]()
Тому що ln y - складна функція, то
![]()
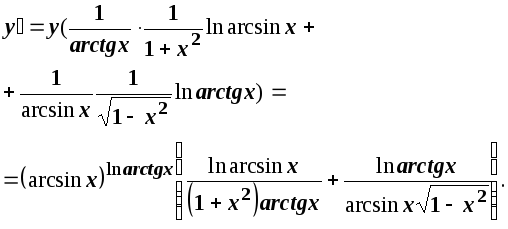
До задачі 4.
Варіант 0:
![]()
Розв’язання.Використовуючи формулу диференціала функції:
![]()
![]()
За формулою диференціала
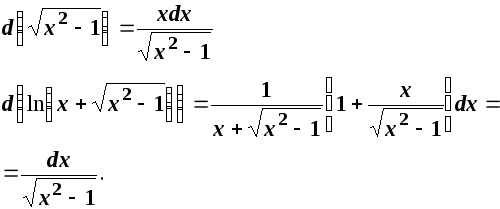
Тоді
![]()
До задачі 5.
Варіант 0: Обчислити наближено.
![]()
Розв’язання.Покладемо
![]()
Тоді за формулою
![]()
запишемо
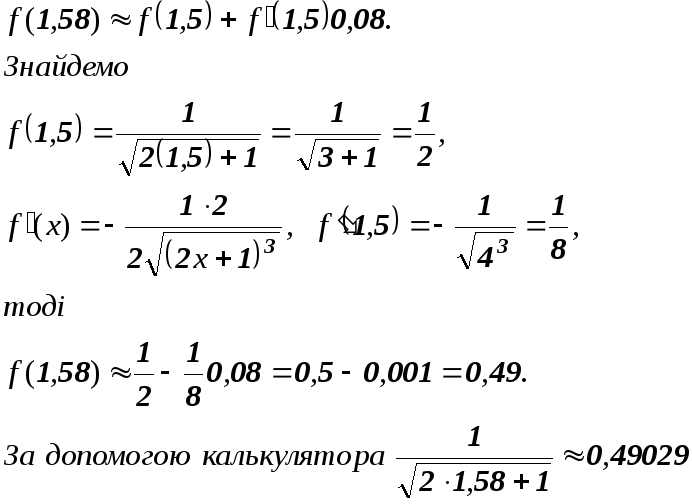 .
.
До задачі 6.
Варіант
0: Знайти
![]()
![]() .
.
Розв’язання.Спочатку знаходимо першу похідну
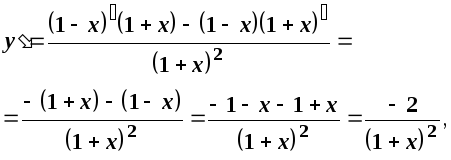
а тоді другу похідну
![]()
До задачі 7.
Варіант
0: Скласти рівняння дотичної та нормалі
до кривої в точці, яка відповідає значенню
параметра
![]() .
.
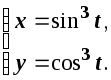
Розв’язання.Рівняння дотичної має вигляд:
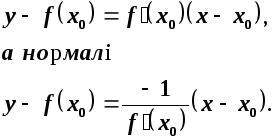
Похідну
функції, заданої параметрично знаходимо
за формулою
![]()
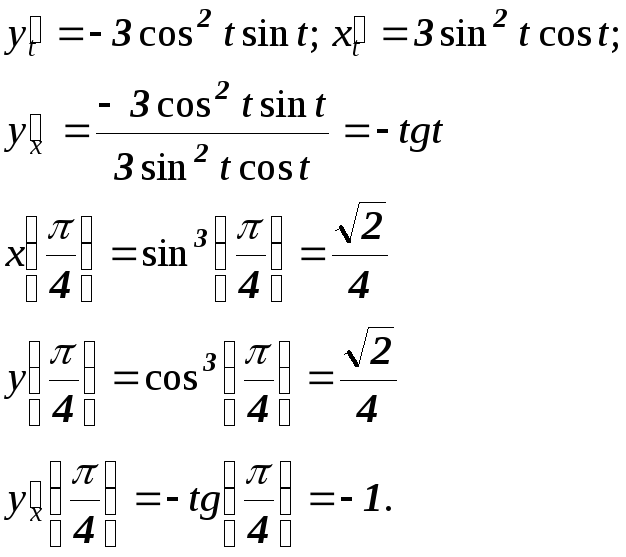
Тепер рівняння дотичної матиме вигляд:
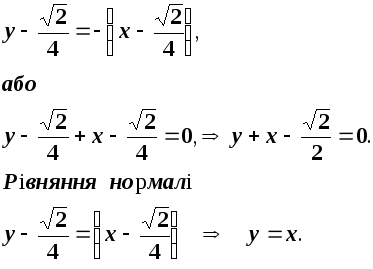
До задачі 8.
Варіант
0. Знайти похідну другого порядку
![]() функції, заданої параметрично.
функції, заданої параметрично.
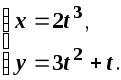
Розв’язання.За правилом диференціювання функції, заданої параметрично маємо:
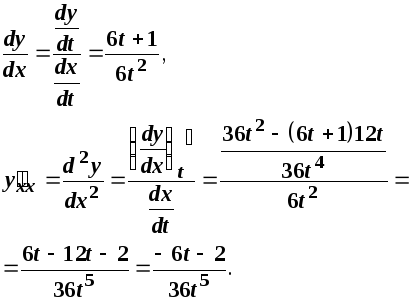
До задачі 9.
Варіант 0. 1. Дослідити функцію і побудовати графік
![]()
Розв’язання.Знайдемо проміжки зростання та спадання функції.
Дана функція має похідну
![]() .
.
Тепер знайдемо точки, в яких похідна дорівнює нулю,
![]()
Ці точки розбивають числову вісь на три інтервали
![]() .
.
Досліджуємо знак похідної на кожному з інтервалів:
![]()
Таким
чином, на інтервалах
![]() функція зростає, а на інтервалі (-1,-2)
функція спадає. Це означає, що точка
функція зростає, а на інтервалі (-1,-2)
функція спадає. Це означає, що точка![]() - точка мінімума,
- точка мінімума,![]() ;
;
![]() - точка максимума,
- точка максимума,
![]() .
Зау Знаходимо важимо, що
.
Зау Знаходимо важимо, що
![]() .
.
Знаходимо
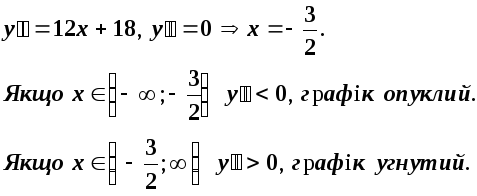
![]()
Точка
![]() є точкою перегину.
є точкою перегину.
6
2,5
-2 -1 0
х
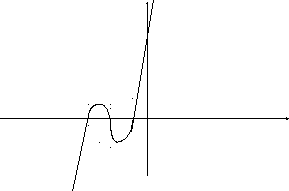 y
y![]()
2. Побудувати графік функції
![]()
Розв’язання.
Функція визначена та неперервна в інтервалах
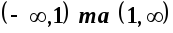
Функція невизначена в точці х = 1.
Знайдемо границі:
![]()
Точки перетину графіка з віссю Х:
![]()
Знайдемо асимптоти графіка функції:
а) х=1 - вертикальна асимптота
б)
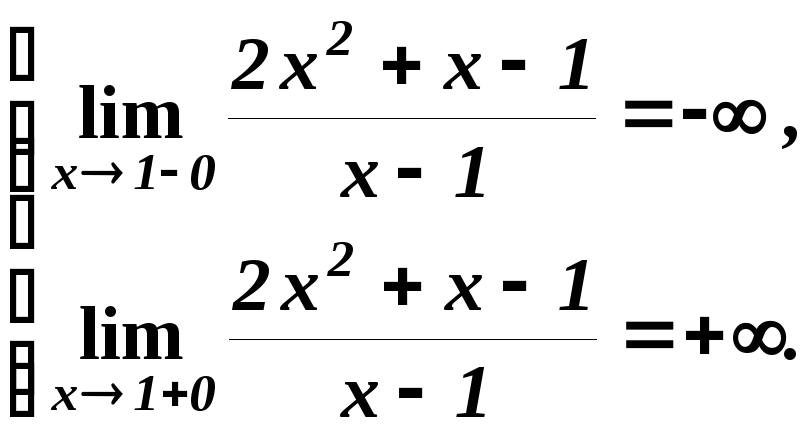
Горизонтальних асимптот немає.
в)

Перевіримо функцію на парність:
![]()
Умови
![]() не виконуються.
не виконуються.
Функція є ні парною, ні непарною.
Знайдемо першу похідну.
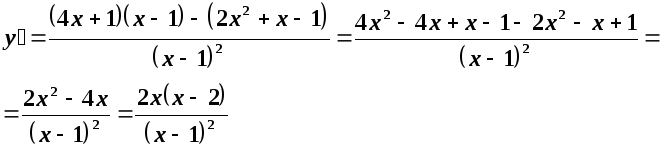 Знаходимо
точки, в яких похідна дорівнює нулю,
Знаходимо
точки, в яких похідна дорівнює нулю,
![]() .
Ці точки розбивають вісь Х на інтервали
.
Ці точки розбивають вісь Х на інтервали
![]() .
Дослідимо знак похідної на кажному з
них :
.
Дослідимо знак похідної на кажному з
них :
![]()
Таким
чином, на інтервалах
![]() функція зростає, а на інтервалі (0,2)
функція спадає; точка
функція зростає, а на інтервалі (0,2)
функція спадає; точка![]() - точка мінімума,
- точка мінімума,![]() ;
;
![]() - точка максимума,
- точка максимума,
![]() .
.
Знайдемо другу похідну
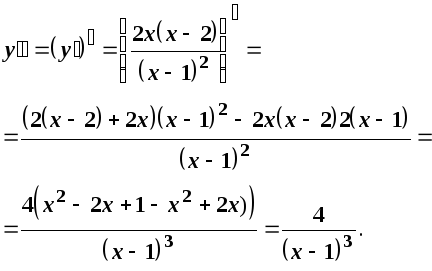
Похідна
![]()
Таким
чином графік функції опуклий для при
![]() і угнутий для
і угнутий для![]() .
.
Будуємо
на площині X0Y
отримані
характерні точки: точки перетину з
осями![]() , вертикальну асимптоту х=0, похилу
асимптоту
, вертикальну асимптоту х=0, похилу
асимптоту
![]() ,
точки екстремума
,
точки екстремума![]() .
Будуємо графік функції.
.
Будуємо графік функції.
9
3
1
-1,5
-1
0 1 2
X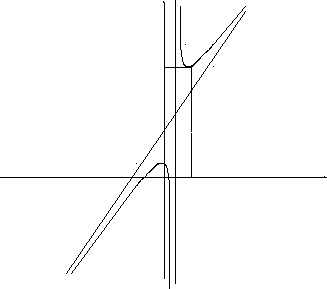 Y
Y![]()
