Приклади

Застосовуючи правило Лопіталя знайти границі:

1. . 2. .

3. . 4..

5. . 6..

Розв’язання

1. .

2. .

3.

.

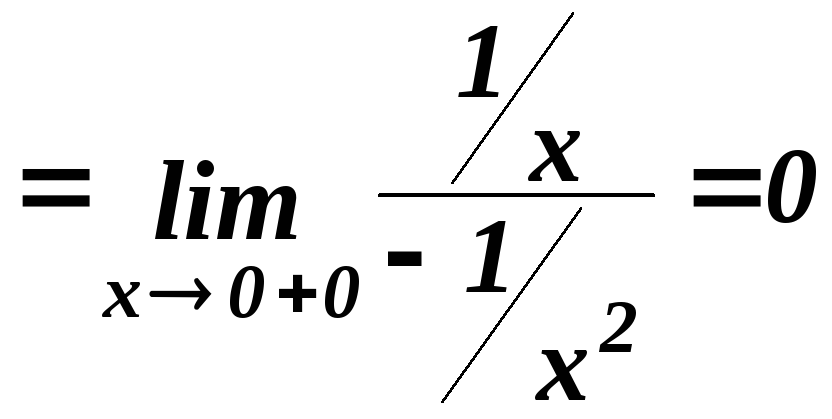4.

.

5. .

Позначимо , а потім про логарифмуємоі знайдемо границю

.

Оскільки для неперервної функції

,

то в даному випадку . Отже,.

6..Покладемо , тоді

,

тобто

.

Приклади для самостійного розв’язання

1. . 2.. 3.

4. . 5.. 6..

7. . 8..

Відповіді:

1. . 2.. 3.. 4.. 5.. 6.. 7.. Вказівка. Невизначеність розкрити шляхом по членного ділення чисельника і знаменника на. Правило Лопітааля не підходить оскільки не існує.8. .

VII. Дослідження функцій

7.1. Зростання і спадання функцій

Означення. Якщо функція y=f(x) така, що більшому значеню аргумента відповідає більше значення функції, то функція y=f(x) називається зростаючою. Аналогічно означається спадна функція.

Зручно відповідно позначити: х) і х.

Теорема 1.

1. Якщо функція f(x), яка має похідну в інтервалі (a, b), зростає на [a, b], то її похідна в інтервалі (a, b) невід’ємна, тобто х.

2. Якщо функція f(x) неперервна на відрізку [a, b] і має похідну в (a, b), причому х> для a<x<b, то ця функція зростає на [a, b].

Y



рис.40 X

Скорочено можна записати:

Доведення. 1. Нехай зростає і в околі точкиіснує скінчена похідна. Розглянемо ліву похідну в цій точці

та праву похідну

.

Оскільки ліва і права похідні збігаються в точці , то із останніх нерівностей випливає.

2. Нехай в околі точки . Застосуємо до різниціформулу Лагранжа

. (1)

Розглянемо два випадки. а) , тоді і права частина, тобто із (1) випливає

- функція зростає

б) , тодіі, із (1) маємо- функція зростає.

Отже, в околі точки (як зліва так і справа) функція зростає, якщо.

Аналогічна теорема має місце, якщо функція f(x) спадає.

Теорема 2.

1. Якщо f(x) має похідну на інтервалі (a, b) i f(x), то х.

2. Якщо f(x) неперервна на [a, b] і має похідну, причому х<,

то f(x) спадає на [a, b].

Y



a b X

рис.41

Скорочено:

Інтервали, на яких функція тільки зростає або тільки спадає називаються інтервалами монотонності.

Отже, з теорем 1 і 2 випливає, що досліджувати функцію на монотонність (зростання і спадання) можна за допомогою похідної, визначаючи знак останньої на окремих проміжках. Раніше (див. ІІ, 2.2) ми досліджували деякі функції на монотонність, встановлюючи знак нерівності міжіпри умові, що. Але такі дослідження зручніше робити за допомогою похідної. Розглянемо на прикладах.

Приклади. Знайти проміжки монотонності функції:

1. . 2..

3. . 4.. 5..

Розв’язання

1. Функція визначена для. Знаходимо похідну. Похідна точок розриву немає і може змінювати знак при переході через корінь

, .

Наносимо коріньна числову вісь, яка при цьому розіб’ється на два інтервали і

()

За допомогою пробних точок визначаємо знак похідної на кожному з інтервалів. Якщо взяти , то- функція спадає.

Якщо , то

- функція зростає.

Отже, для ;

для .

2. -функція визначена для всіх . Її похідна

має корені і, які розбивають числову вісь на три інтервали

, ,

Підставляючи пробні точки у розклад похідної на множники , визначаємо її знак у кожному із інтервалів (див. рис.). У відповідності до знаку похідної на даному інтервалі робимо висновок про поведінку функції:

, функція зростає;

, функція спадає;

, функція зростає.

3. - функція не існує у точках . Знаходимо похідну

.

Корені похідної ,та її точки розривуірозбивають числову вісь на 5 інтервалів, визначаємо знак похідної на кожному з них:

, функція спадає;

, функція зростає;

, функція зростає;

, функція спадає;

, функція спадає.

Тут числа - це пробні точки, з відповідних інтегралів, у яких визначався знак похідної.

4. Функція існує для всіх, її похідна

.

Оскільки похідна невід’ємна, то дана функція неспадна для всіх .

5. Знайдемо спочатку область існування (визначення) функції ,

. Функція існує на проміжку . Похідна функції має вигляд

;

- корінь похідної, яка до того має таку область існування .

Для , функція зростає;

Для , функція спадає.

Відмітимо ще, що за допомогою похідної можна доводити деякі нерівності.

Приклади. Довести нерівності.

6. . 7..

8. .

9. .