44. Математический формализм квантовой механики

45.Матримца плотности. Операторы

Матрица плотности (оператор плотности, оператор матрица плотности, статистический оператор) – один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в равной мере может задавать как чистые, так и смешанные состояния.

Использование оператора плотности становится необходимым, если состояние квантовомеханической системы по тем или иным причинам не может быть рассмотрено как чистое. Такое положение имеет место, в частности, в квантовой статистике. При этом оператор плотности оказывается естественным аналогом фигурирующей в классической статистической механике функции распределенияплотности в фазовом пространстве. Кроме того, существует трактовка квантовомеханической процедуры измерения как перехода из исходного чистого состояния в смешанное состояние

,

где суть отвечающие выбранному полному набору измеряемых величин базисные векторы.

46.СВОЙСТВА ВОЛНОВОЙ ФУНКЦИИ Не всякая мат-я ф-я может быть волн функ-й. К волн ф-ция опред определенной требование, из кот-й

1.Волн ф-я обязат однознач т.е одному аргументу соот только одно значение ф-ции

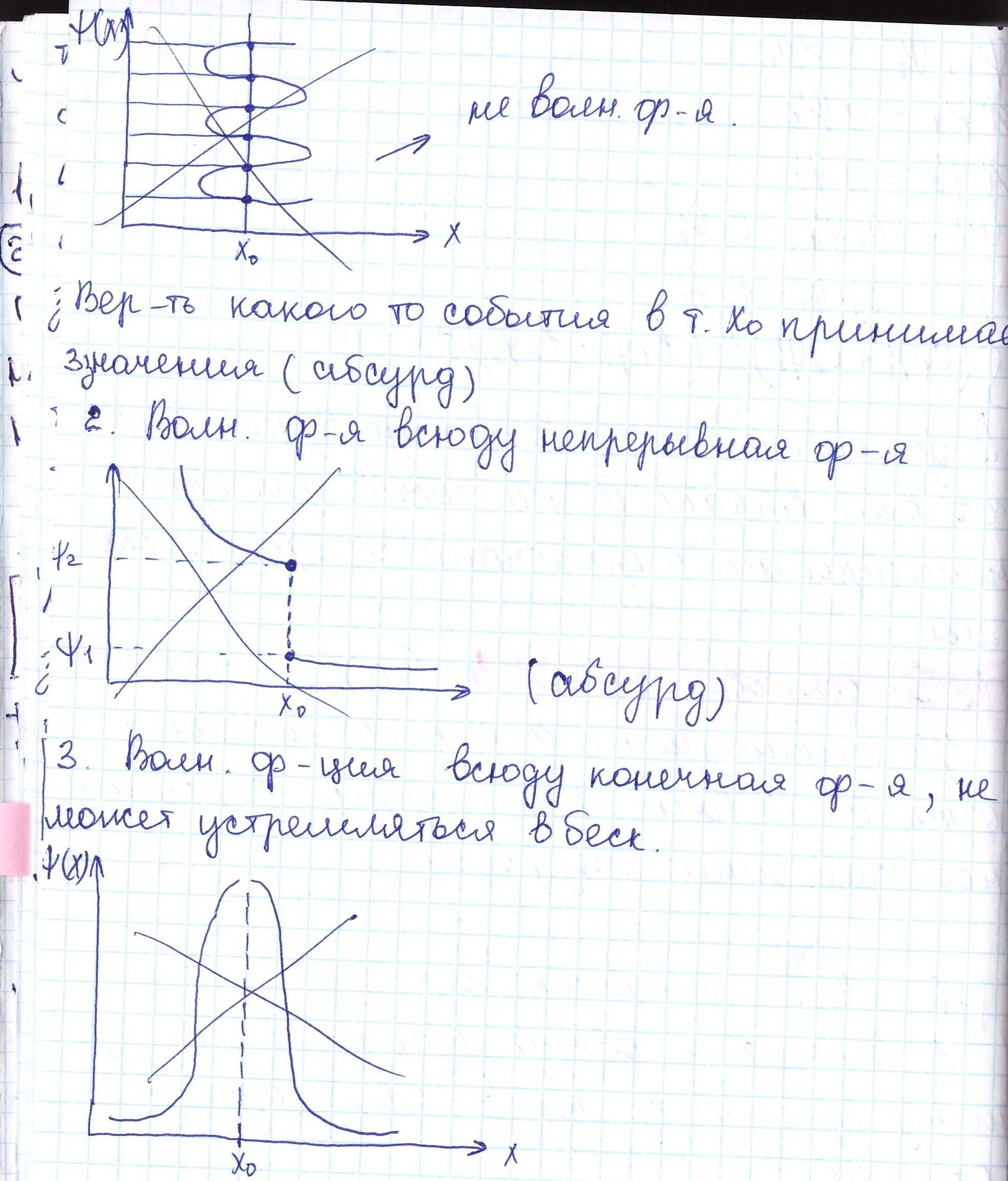
6. Волн ф-я имеет непрерывную первую производ по всем переменным от кот-х она зависит, т.к. в ур-е Шредингера входят вторая производная, если 1 производ испыт скачок, то 2 произв в т. Скачка не сущ-ет, что яв-ся абсурдом, т.к опыт Шредингера з-н природы

47 Теорема об ортогональности собственных функци

48. ПРИНЦИП НЕОПРЕДЕЛЕННОСТИ

49.УСЛОВИЯ ОДНОАРЕМЕННОЙ ИЗМЕРИМОСТИ ФИЗИЧЕСКИХ ВЕЛИЧИН

НАБОРОМ ФИЗ.ВЕЛИЧИН

50.СООТНОШЕНИЕ НЕОПРЕДЕКЛЕННОСТИ

Эта ошибка зависит от прибора (систематич.ошибка)

1. Это ошибка зависит с волновым свойством микрочастиц.

2. Любое изм. всегда есть воздейстие на объект (в классич.физ.по умолчанию,т.е. процесс измерения не отраж.) на скорости. В микромире прорцесс меняет сост. системы.

Из этого соотношения в частности следует: если мы знаем коммутаторы динамич. величин, мы можем определить ли две вечины, мы можем сказать какие входят в полный режим.

51.ПРИНЦИП ДОПОЛНИТЕЛЬНОСТИ

Мы можем подобрать набор величин, операторы которых коммутируют между собой, такой набор называется полным набором физических величин.

52.ОСНОВЫ ТЕОРИИ ПРЕДСТАВЛЕНИЯ

Трёхмерный вектор однозначно задаётся тройкой компонент (проекций) вектора на три неэквивалентных направления в пространстве:,и. Сумма двух векторов в пространствеи– есть новый вектор, составленный из сумм одноимённых компоненти, тогда соответственно:

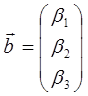
таким образом:

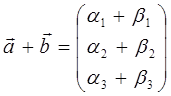
Умножение вектора на скаляр (число), есть «растяжение» векторавраз и отвечает новому вектору вида:

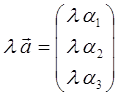
Для пары действительных векторов ивводится числовая характеристика – скалярное произведение. При скалярном перемножении двух векторов получают скаляр (число):

равное сумме произведений их проекций и. Модулем (длиной) вектораназывают выражение вида:

здесь:

53.Разложение по собственным функциям

54.ПОНЯТИЯ О ПРЕДСТАВЛЕНИЯХ

55.ВЫЧИСЛЕНИЕ СРЕДНИХ ЗНЧЕНИЙ ФИЗИЧЕСКИХ ВЕЛИЧИН

,6

56 ДИНАМИЧЕСКИЕ ПЕРЕМЕННЫЕ КВАНТОВОЙ МЕХАНИКИ

57.ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ Коммутаторы динамических величин и операторы называют перестановочными соотношениями:

=?

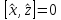
Все x, y, z могут быть определены одновременно и точно.

2)

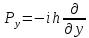
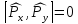
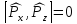
Это значит 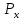, ,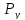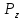определяются одновременно и точно, т.е. можно задавать однозначно

3)

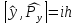
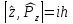
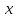, – одновременно и точно не определяются

–соотношение неопределенности (корпускулярно-волновой дуализм)

58. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРОВ ДИНАМИЧЕСКИХ ВЕЛИЧИН

59.УРАВНЕНИЯ ШРЕДИНГКРА

60.СТАЦИОНАРНЫЕ СОСТОЯНИЯ, ОДНОМЕРНЫЕ ЗАДАЧИ

§19. Стационарные состояния. Одномерные задачи

Пусть потенциальное поле не зависит от времени (стационарно) 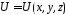. В этом случае уравнение Шредингера допускает разделение переменных пространственных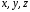и времениt. Действительно, представим волновую функцию в виде:=f (t)₀(x, y, z), подставим это выражение в уравнение Шредингера и разделим обе части на .

Уравнение приобретает вид: 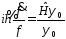, т.к. левая часть этого уравнения зависит только от времени, а правая – только от координат, то обе должны быть равны одной и той же постоянной Е, имеющей размерность энергии. В итоге получаем уравнения: 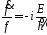(6.1)

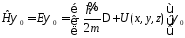. (6.2)

Решение (6.1) имеет вид: 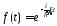(постоянный множитель оставляем в₀). Сравнивая с волной де Бройля, видим, что постоянная должна представлять энергию частицы. Это подтверждается видом уравнения (6.2), в котором в левой части стоит оператор Гамильтона (полной энергии частицы).

Решения вида: 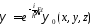определяют так называемые стационарные состояния. Легко видеть, что в таких состояниях и вероятность и плотность тока вероятности не зависят от времени, поскольку произведение.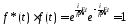

Уравнение 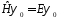называется уравнением Шредингера для стационарных состояний в отличие от временнóго (5.6). В дальнейшем (за исключением теории излучения) мы будем иметь дело, главным образом, с этим уравнением и₀ обозначать просто , не забывая, когда нужно умножать на временнýю экспоненту.

В случае, если волновая функция зависит только о одной координаты уравнение Шредингера принимает вид:

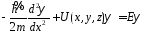или . (6.3)

Это уравнение однородное уравнение второго порядка нам хорошо известно. Его решениями являются при E>U суперпозиция гармонических функций , где(тип А), а приU>E суперпозиция экспонент с действительным показателем , где(тип Б). Константы при экспонентах определяются в каждой задаче из конкретных граничных условий.

Рассмотрение одномерных задач более простых полезно т.к. уравнение Шредингера допускает разделение переменных, в декартовых координатах это бывает тогда, когда , но нам придется иметь дело и с разделением переменных в сферических координатах.