1.Основные понятия и определения электродинамики

Электродинамика – это наука о свойствах и закономерностях особого вида материи – электромагнитного поля, которое осуществляет взаимодействие между электрическими заряженными телами или частицами.

Ква́нтовая электродина́мика (КЭД) — квантовополевая теория электромагнитных взаимодействий; наиболее разработанная часть квантовой теории поля. Классическая электродинамика учитывает только непрерывные свойства электромагнитного поля, в основе же квантовой электродинамики лежит представление о том, что электромагнитное поле обладает также и прерывными (дискретными) свойствами, носителями которых являются кванты поля —фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание частицами фотонов.

2.Характеристики электромагнитного поля

Электромагнитное поле – Е = Н/Кл = В/М

E= F/q – отношение силы, действующей со стороны поля к величине этого заряда.

D- индукция электрического поля – называется вектор пропорциональный вектору напряженности, но независящий от свойств среды

D = 𝞮E; 𝞮=𝞮₀𝞮’ ₀= 8.85 * 10^-12 Ф/м

В- вектор индукции магнитного поля = Н/А*м= 1Тл

Индукцией называется вектор, модуль которого есть отношение модуля силы действующий со стороны поля на проводник с током, на силу тока в проводнике и его длину. B= |F|/ I*l (Н/ А*м) Н – напряженность магнитного поля (А/м) = 80 эрстед =) 80 Гаусс, называется вектор параллельный вектору индукции, но независящий от свойств среды. Н= 1/µ, где µ = µ_0* µ’

3.Векторные поля.Интегральные и дифферциальные характеристики векторного поля

4.ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА И СТОКСА

5.ЗАКОН КУЛОНА

6.ТЕОРЕМА ГАУССА

7.ПОТОК ВЕКТОРА

8.УРАВНЕНИЯ НЕПРЕРЫВНОСТИ

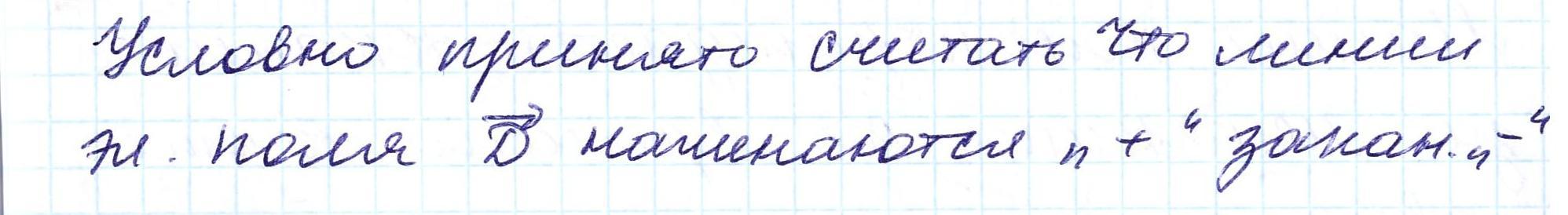
9.ТОК СМЕЩЕНИЯ

10.ЗАКОН ПОЛНОГО ТОКА

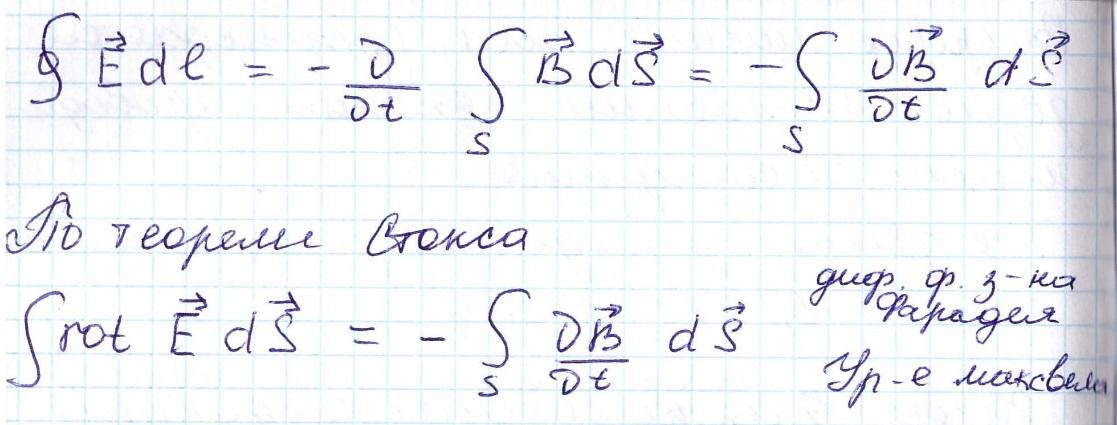
11.ЗАКОН НЕПРЕРЫВНОСТИ МАГНИТНОГО ПОТОКА

12.ГРАНИЧНЫЕ УСЛОВИЯ

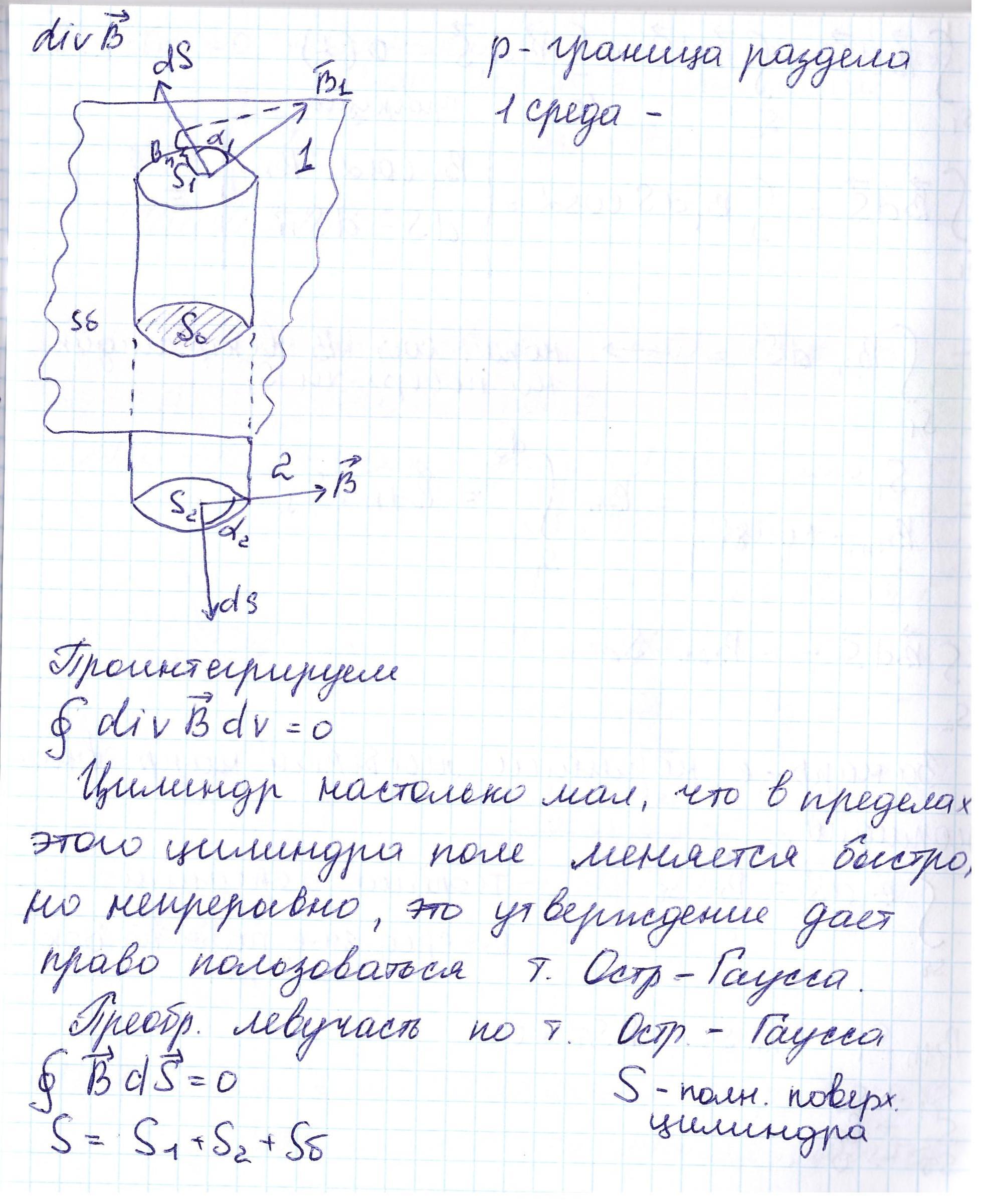
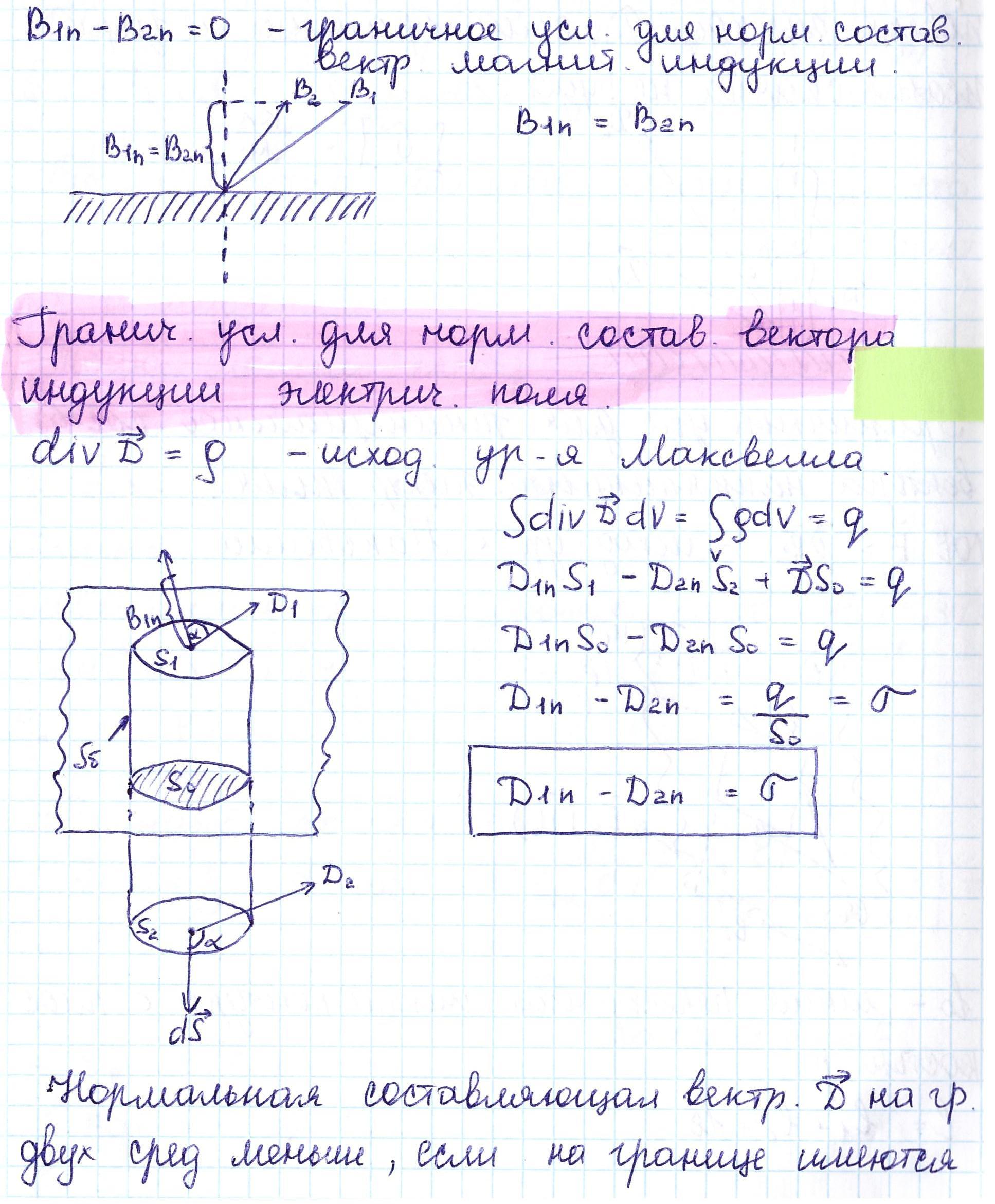
13.ЗАКОНЫ ДЖОУЛЯ-ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

Количество теплоты, выделяющееся в единицу времени в проводнике с сопротивлением R при силе тока I, по закону Джоуля-Ленца, равно:

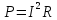
Применив этот закон к бесконечно малому цилиндру, ось которого совпадает с направлением тока, получаем

Учитывая что 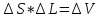– обьем бесконечно малого цилиндра, а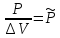– количество теплоты, выделенной в единице обьема за единицу времени, находим

,

Где 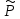выражается в ватах на кубический метр. Учитывая, что j²=j*j и используя для j выражение 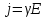можно записать соотношение в виде:

Это равенство выражает закон Джоуля-Ленца в дифференциальной форме.

14.Полная система уравнений максвелла в веществе

В среде сторонние электрические и магнитные поля вызывают поляризацию и намагничивание вещества, которые макроскопически описываются соответственно вектором поляризации P и вектором намагниченности M вещества, и вызваны появлением связанных зарядо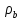в и токов . В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.

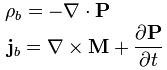
Поляризация P и намагниченность вещества M связаны с векторами напряжённости и индукции электрического и магнитного поля следующими соотношениями:

Поэтому, выражая векторы D и H через E, B, 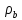и 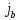 , можно получить математически эквивалентную систему уравнений Максвелла:

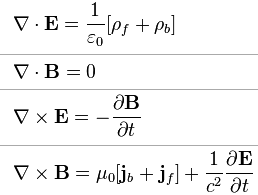
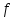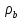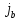Индексом здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в ,, а затем в P, M и, следовательно, в D, B сложный микроскопический характер электромагнитного поля в среде.