§ 10. Спектр симметричного оператора Ортогональные дополнения подпространств евклидова пространства

Пусть U, W – два подпространства в векторном пространстве V, причем U  W = {0} и  v  V  u  U , w  W v = u + w, т.е. V = U + W. Тогда говорят, что пространство V является прямой суммой подпространств U и W и пишут V = U  W.

Примеры: 1. Пусть V = V₂(O, R) – множество всех векторов плоскости, отложенных от т. О, и на плоскости задана аффинная система координат с центром в т. О, U = { u  V | u лежит на оси ОХ }, W = { w  V | w лежит на оси ОY }. Тогда V = U  W (?!).

2. Пусть V = R³. Рассмотрим подпространства

U = {(u₁ ; u₂ ; u₃)  R³ | u₁ + u₂ + u₃ = 0}, W = {(w₁ ; w₂ ; w₃)  R³ | w₁ = w₂ = 0}

(почему они будут подпространствами в V ?!). Тогда V = U  W . Действительно, если v = (v₁ ; v₂ ; v₃)  U  W, то , т.е.v₁ = v₂ = = v₃ = 0, и U  W = {0}. Справедливость равенства U + W = V следует из представления (v₁ ; v₂ ; v₃) = (v₁ ; v₂ ; –v₁ – v₂) + (0; 0; v₃ + v₁ + v₂)  U + W.

Упражнение. Докажите, что (V = U  W)  ( v  V  ! u  U, w  W v = u + w).

Теорема (об ортогональном дополнении). Пусть (V, (_, _)) – евклидово пространство, U – его конечномерное подпространство. Тогда

U^ = {w  V |  u  U (u , w) = 0 }

является подпространством в V, причем V = U  U^. Пространство U^ называется ортогональным дополнением к U в пространстве V.

Доказательство. Прежде всего, U^ , т.к. 0  U^. Кроме того, U^ замкнуто относительно сложения и умножения на скаляры. В самом деле, если w₁ , w₂  U^,   R, то для любого u  U имеем:

(u , w₁ + w₂) = (u , w₁)+(u , w₂ ) = 0+0 = 0, (u , w₁) = (u , w ₁) = 0 = 0.

По лемме о подпространстве, U^ – подпространство в V.

Докажем, что V = U  U^. Пусть v  U  U^. Тогда по определению U^ имеем (v , v) = 0, и v = 0 из неотрицательности скалярного произведения. Итак, U  = {0}. Осталось проверить, что V = U + U^. Если U = {0}, то U^ = V, и доказывать нечего. Если же U  {0}, то (по теореме об ортонормированном базисе) можно выбрать ортонормированный базис e = (e₁ , … , e_n ) в U. Пусть v  V и u = (v , e₁ )e₁ + … + (v , e_n)e_n  U, g = v – u . Тогда, как и в теореме об ортонормированном базисе, убеждаемся, что g  e_i (1  i  n), т.е. g  U^ (?!) и v = u + g  U + U^.

Теорема доказана.

Примеры: 1. Найти ортогональное дополнение к подпространству U, порожденному векторами u₁ = (0; 1; –1; 1) и u₂ = (–1; 0; 0; 1) стандартного евклидова пространства R⁴.

Так как U^ = {w  R⁴ |  u  U (u , w) = 0 }, то

((w₁ ; w₂ ; w₃ ; w₄)  ) .

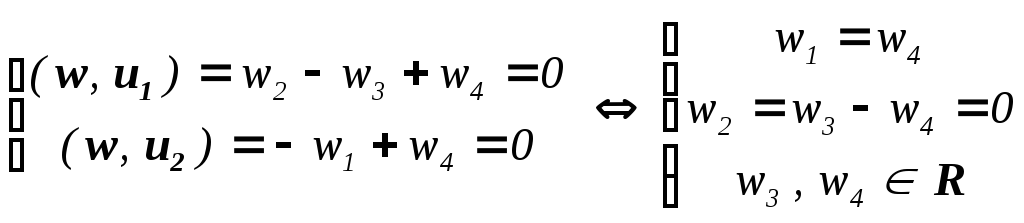Таким образом, U^ = { (w₄ ; w₃ – w₄ ; w₃ ; w₄)  R⁴ | w₃ , w₄  R }. Базисом является фундаментальная система решений рассмотренной однородной системы линейных уравнений, получающаяся из найденного общего решения при значениях свободных переменных w₃ = 1, w₄ = 0 и w₃ = 0, w₄ = 1 – а именно система векторов (0; 1; 1; 0), (1; –1; 0; 1).

2. Пусть V = V₂(O, R) со стандартным скалярным произведением (a , b) = = |a||b|cos( a ,b). Если U = { u  V | u лежит на прямой y = 2x }, то легко доказать, что U^= { w  V | w лежит на прямой y = – 0,5x } (?!).