§ 6. Инвариантные подпространства линейного оператора
Пусть : V V – линейный оператор, W – подпространство в V. Оно называется -инвариантным, если w W (w) W. Будем использовать обозначение W V.
Примеры. 1. Очевидно, что {0} V и V V для любого линейного оператора : V V .
2. Если : V V – линейный оператор, то Ker() V и Im() V , т.к. k Ker() (k) = 0 Ker() и v Im() (v) Im().
3.
Пусть линейный оператор
: V
V
имеет в базисе {e1
, e2
, e3}
матрицу
. Тогда
пространство L(e1
, e2)
является
-инвариантным.
Действительно, по определению матрицы линейного оператора имеем
(e1)
= (e1
, e2
, e3)
= –e1
+ 2e2
L(e1
, e2),
(e2)
= (e1
, e2
, e3)
= =e1
– 2e2
L(e1
, e2)
и поэтому
l
= 1e1
+ 2e2
L(e1
, e2)
верно
включение (l)
= 1(e1)
+ 2(e2)
L(e1
, e2).
Оказывается, пример 3 отражает общую ситуацию, как показывает следующая
Лемма (об инвариантных подпространствах линейного оператора). Следующие условия для линейного оператора : V V и подпространства W в n-мерном векторном пространстве V эквивалентны:
(1) подпространство W является -инвариантным,
для некоторого базиса (w1 , … , wk) пространства W выполнены условия (wi) W (1 i k).
Кроме того, эквивалентны следующие утверждения:
(3) существует собственное -инвариантное подпространство W (т.е. {0} W V, (W) W),
(4)
в некотором базисе e
= (e1
, … , en)
пространства V
матрица линейного оператора
имеет полураспавшийся вид []e
=
,
гдеA
M(k,
F),
B
M(n
– k,
F),
C
M(k,
n
– k,
F).
Доказательство. (1) (2) Если W – -инвариантное подпространство, то w W (w) W. В частности, это выполнено и для векторов любого базиса (w1 , … , wk) пространства W.
(2) (1) Пусть теперь для векторов некоторого базиса (w1 , … , wk) пространства W выполнено условие (wi) W (1 i k). Докажем, что w W (w) W: если w = 1w1 + … + kwk – разложение по базису, то (w) = = 1(w1)+…+k(xk) W.
(3)
(4) Пусть W
– собственное -инвариантное
подпространство с базисом {e1
, … , ek}
и 0
< dim
W
= k
< dim
V
= n.
Дополним этот базис до базиса всего
пространства V
векторами ek+1
, … , en
и рассмотрим
матрицу линейного оператора
в
расширенном базисе e
= (e1
, … , ek
, ek+1
, … , en
). Имеем
[]e
=
,
где A
M(k, F), B
M(n – k, F), C
M(k, n – k, F) и
D
M(n – k, k, F).
Первые k её
столбцов – это координатные столбцы
[(e1)]e
, … , [(ek)]e
, причём ввиду -инвариантности
подпространства W
= L(e1
, … , ek)
выполнены
включения (ei)
L(e1
, … , ek)
(1
i
k). Таким
образом, (ei)
= a1ie1
+ … + akiek
+ 0ek+1
+ … 0en
, т.е. D
= 0(n–k)k
и матрица оператора полураспавшаяся
в выбранном базисе.
(4)
(3) Пусть в
некотором базисе e
= (e1
, … , ek
, ek+1
, … , en
) пространства
V
матрица []e
полураспавшаяся
[]e
=
.
Докажем, что пространство W
= L(e1
, … , ek)
является
-инвариантным
подпространством в V.
Действительно,
(ei)
= (e1
, … , ek
, ek+1
, … , en)[]e(i)
= (e1
, … , ek
, ek+1
, … , en)
=
= (e1 , … , ek)a(i) = a1ie1 + … + akiek L(e1 , … , ek) = W.
Таким образом, подпространство W является -инвариантным.
Лемма доказана.
Упражнения:
1. Найдите
все
инвариантные подпространства линейного
оператора
: V
V
с матрицей []e
=
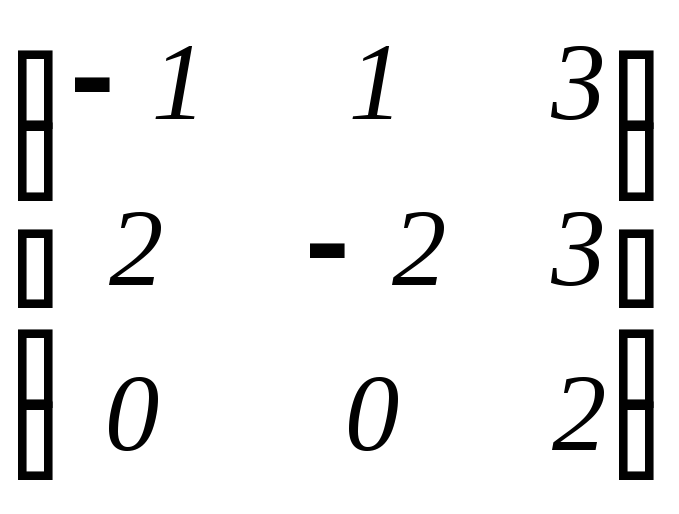в некотором базисе {e1
, e2
, e3}.
2.
Найдите все
инвариантные подпространства линейного
оператора
: V
V
с матрицей []e
=
в некотором базисе {e1
, e2
, e3}.
Особенно часто используются одномерные инвариантные подпространства, к изучению которых мы сейчас переходим.