Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

“Тобольская государственная социально-педагогическая академия

им. Д.И. Менделеева”

Кафедра математики, ТиМОМ

Валицкас А.И.

ОСНОВЫ МАТЕМАТИЧЕСКИХ

НАУК

Тобольск – 2012

С О Д Е Р Ж А Н И Е

Глава III.	Евклидовы пространства . . . . . .	3
	§ 1. Определения, примеры и простейшие свойства . .	3
	§ 2. Длины и углы в евклидовых пространствах . .	6
	§ 3. Ортогональные базисы евклидовых пространств . .	8
	§ 4. Изоморфизм евклидовых пространств . .	10
Глава IV.	Линейные операторы в векторных пространствах .	13
	§ 1. Определение и простейшие свойства . . . .	13
	§ 2. Матричный формализм в векторных пространствах .	19
	§ 3. Матрица перехода от базиса к базису . . . .	24
	§ 4. Матрица линейного оператора . . . . .	27
	§ 5. Образ, ядро, ранг и дефект линейного оператора . .	31
	§ 6. Инвариантные подпространства линейного оператора .	36
	§ 7. Собственные числа и векторы линейного оператора .	39
	§ 8. Подобные матрицы и их спектральные задачи . .	45
	§ 9. О подобии матриц . . . . . .	47
	§ 10. Спектр симметричного оператора . . . .	55
Глава V.	Дифференцирования в банаховых пространствах .	63
	§ 1. Метрические и банаховы пространства . . .	63
Литература	. . . . . . . . . . .	74

Глава III. Евклидовы пространства

§ 1. Определения, примеры и простейшие свойства

Пусть V – векторное пространство над R . Скалярным произведением на V называется отображение от двух аргументов (_ , _) : VV R , обладающее следующими свойствами:

1. свойство неотрицательности:  v  V \ {0} (v , v) > 0,

2. свойство аддитивности по первому аргументу:

 u, v, w  V (u + v , w) = (u , w) + (v , w),

3. свойство однородности по первому аргументу:

 u, v  V    R (u , v) =  (u , v),

4. свойство симметричности:  u, v  V ( u , v) = ( v , u) .

Примеры: 1. Пусть V = R². Если для u = (x₁ , x₂)  V, v = (y₁ , y₂)  V определить (u , v) формулой (u , v) = x₁y₁ + x₂y₂ , то нетрудно понять, что таким образом будет задано скалярное произведение на R² (?!). Это скалярное произведение не единственно: например, можно было задать на V другое скалярное произведение (u , v) = x₁ y₁ + 2x₂y₂ .

2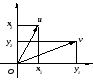. Пусть V = V₂(O, R) – векторное пространство всех направленных отрезков плоскости, отложенных от фиксированной точки О. Тогда скалярное произведение на V можно задать формулой (u , v) = |u||v|cos, где  – угол между векторами u и v. В этом можно убедиться, например, так: введя на плоскости прямоугольную систему координат с центром в точке О (см. рис.), получим

(u, v) = x₁y₁+x₂y₂ = |u|cos(+)|v|cos + |u|sin(+)|v|sin =

= |u||v|[cos(+)cos + sin(+)sin] = |u||v|[coscos² – sinsincos +

+ sinsincos + cossin²] = |u||v|cos .

Поэтому можно воспользоваться предыдущим примером. А как можно проще проверить свойства этого скалярного произведения ?

3. Предыдущие примеры можно обобщить на другие пространства, например, на V = R³ и V = V₃(O, R) (как ?!).

4. Формула (u, v) = x₁y₁ + … + x_ny_n задаёт скалярное произведение векторов u = (x₁ ; … ; x_n), v = (y₁ ; … ; y_n) пространства Rⁿ, называемое стандартным. Аналогично определяется стандартное скалярное произведение векторов пространства ⁿR .

5. Пусть V = { f : [0, 1] R | f непрерывна и интегрируема на [0, 1]}. Тогда формула (f, g) = задаёт скалярное произведение на V.

Упражнения: 1. При каких условиях на коэффициенты a, b, c, d, e  R формула ( u , v) = ax₁y₁ + bx₁y₂ + cx₂y₁ + dx₂y₂ + e задаёт скалярное произведение в R² ?

2. Будет ли ( u , v) = x₁y₁ + … + x_n–1y_n–1 – x_ny_n скалярным произведением в Rⁿ ?