
- •ВВЕДЕНИЕ
- •ГЛАВА 1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
- •§1. ОПРЕДЕЛИТЕЛИ
- •Пример 1.1.
- •Задания для самостоятельного решения.
- •Задание 1.1.
- •а) разложив его по элементам i-й строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-й строке.
- •§2. МАТРИЦЫ
- •Пример 1.2.
- •Задания для самостоятельного решения.
- •Задание 1.2.
- •Даны две матрицы А и В.
- •§3. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •Пример 1.3.
- •Пример 1.4.
- •Пример 1.5.
- •Пример 1.6.
- •Задания для самостоятельного решения.
- •Задание 1.3.
- •Задание 1.4.
- •В заданиях 1.5-1.6 решить однородную систему линейных алгебраических уравнений.
- •Задание 1.5.
- •Задание 1.6.
- •§4. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ
- •Пример 1.7.
- •Пример 1.8.
- •Задания для самостоятельного решения.
- •Задание 1.7.
- •Решить матричное уравнение и сделать проверку
- •ГЛАВА 2 ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- •Пример 2.1
- •Пример 2.2
- •Пример 2.3
- •Пример 2.4
- •Пример 2.5
- •Задания для самостоятельного решения.
- •Задание 2.1.
- •Задание 2.2.
- •Задание 2.3
- •Задание 2.4.
- •Задание 2.5.
- •ГЛАВА 3 ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
- •§1. ПРЯМАЯ НА ПЛОСКОСТИ
- •Пример 3.1
- •Задания для самостоятельного решения.
- •Задание 3.1.
- •§2. ПЛОСКОСТЬ В ПРОСТРАНСТВЕ
- •Пример 3.2
- •Пример 3.3
- •Пример 3.4
- •Задания для самостоятельного решения.
- •Задание 3.2
- •Задание 3.3
- •Задание 3.4
- •Найти угол между плоскостями.
- •§3 ПРЯМАЯ В ПРОСТРАНСТВЕ
- •Пример 3.5
- •Задания для самостоятельного решения.
- •Задание 3.5
- •Написать каноническое уравнение прямой.
- •§4. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
- •Пример 3.6
- •Пример 3.7
- •Пример 3.8
- •Задания для самостоятельного решения.
- •Задание 3.6
- •Найти точку пересечения прямой и плоскости.
- •Задание 3.7
- •§5. КРИВЫЕ ВТОРОГО ПОРЯДКА
- •Пример 3.9
- •Пример 3.10
- •Пример 3.11
- •Пример 3.12
- •Пример 3.13
- •Пример 3.14
- •Задания для самостоятельного решения.
- •Задание 3.8.
- •ГЛАВА 4 ВВЕДЕНИЕ В АНАЛИЗ
- •§ 1. ПРЕДЕЛЫ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
- •Пример 4.1
- •Задания для самостоятельного решения.
- •Задание 4.1
- •Вычислить пределы числовых последовательностей.
- •§ 2. ПРЕДЕЛЫ ФУНКЦИЙ
- •Пример 4.2
- •Вычислить пределы дробно-рациональных функций:
- •Пример 4.3
- •Задания для самостоятельного решения.
- •Задание 4.2.
- •Вычислить пределы дробно-рациональных функций
- •Задание 4.3.
- •Вычислить пределы иррациональных функций
- •§ 3. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ.
- •Пример 4.4
- •Пример 4.5
- •Пример 4.6
- •Задания для самостоятельного решения.
- •Задание 4.4.
- •Вычислить пределы, используя первый замечательный предел и его следствия.
- •Задание 4.5.
- •Задание 4.6
- •§ 4. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
- •Пример 4.7
- •Пример 4.8
- •Задания для самостоятельного решения.
- •Задание 4.7.
- •Задание 4.8.
- •§ 1.ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
- •Пример 5.1
- •Пример 5.2
- •Пример 5.3
- •Пример 5.4
- •Пример 5.5
- •Пример 5.6
- •Пример 5.7
- •Пример 5.8
- •Пример 5.9
- •Пример 5.10
- •Пример 5.11
- •Пример 5.12
- •Пример 5.13
- •Задания для самостоятельного решения.
- •В заданиях 5.1-5.13 вычислить производные функций, используя таблицу производных и правила дифференцирования.
- •Задание 5.1
- •Задание 5.2.
- •Задание 5.3.
- •Задание 5.4.
- •Задание 5.5.
- •Задание 5.6.
- •Задание 5.7.
- •Задание 5.8.
- •Задание 5.9.
- •Задание 5.10.
- •Задание 5.11.
- •Задание 5.12.
- •Задание 5.13.
- •§ 2. ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ
- •Пример 5.14
- •Пример 5.15
- •Пример 5.16
- •Задания для самостоятельного решения.
- •В заданиях 5.14-5.16 вычислить следующие производные, используя метод логарифмического дифференцирования
- •Задание 5.14.
- •Задание 5.15.
- •Задание 5.16
- •§ 3. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ, ЗАДАННЫХ НЕЯВНО И ПАРАМЕТРИЧЕСКИ
- •Пример 5.17
- •Пример 5.18
- •Задания для самостоятельного решения.
- •Задание 5.17.
- •Задание 5.18.
- •§4. ПРАВИЛО ЛОПИТАЛЯ
- •Пример 5.19
- •Пример 5.20
- •Задания для самостоятельного решения.
- •Найти указанные пределы, используя правило Лопиталя.
- •Задание 5.19
- •Задание 5.20.
- •§ 5. ПОЛНОЕ ИССЛЕДОВАНИЕ ФУНКЦИЙ
- •Пример 5.21
- •Пример 5.22
- •Пример 5.23
- •Задания для самостоятельного решения.
- •Провести полное исследование функций и построить их графики
- •Задание 5.21.
- •Задание 5.22.
- •Задание 5.23.
- •§ 6. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛА ДЛЯ ПРИБЛИЖЕННОГО ВЫЧИСЛЕНИЯ
- •Пример 5.24
- •Пример 5.25
- •Задания для самостоятельного решения.
- •С помощью дифференциала приближенно вычислить данные величины и оценить допущенную относительную погрешность (с точностью до двух знаков после запятой).
- •Задание 5.24.
- •Задание 5.25.
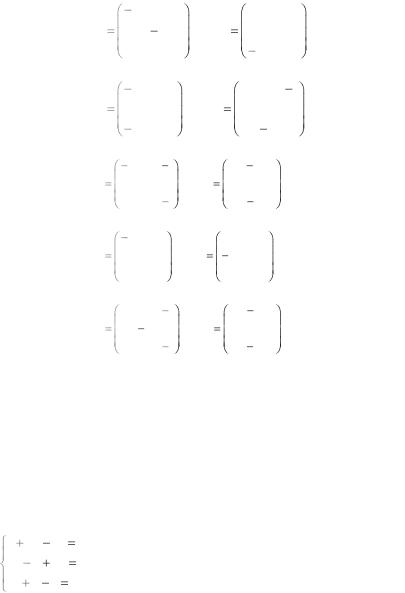
|
|
3 |
4 |
2 |
|
|
1 |
4 |
4 |
26. |
A |
1 |
5 |
3 |
, |
B |
1 |
3 |
2 . |
|
|
0 |
1 |
2 |
|
|
4 |
1 |
2 |
|
|
3 |
4 |
0 |
|
1 |
7 |
1 |
27. |
A |
4 |
5 |
1 |
, |
B 0 |
2 |
6 . |
|
|
2 |
3 |
3 |
|
2 |
1 |
1 |
|
|
3 |
4 |
3 |
|
2 |
2 |
0 |
|
28. |
A |
1 |
2 |
3 |
, |
B |
5 |
4 |
1 . |
|
|
5 |
0 |
1 |
|
1 |
1 |
2 |
|
|
|
1 |
0 |
2 |
|
|
3 |
0 |
1 |
29. |
A |
2 |
3 |
2 |
, |
B |
3 |
1 |
7 . |
|
|
3 |
7 |
1 |
|
|
1 |
3 |
2 |
|
|
4 |
1 |
4 |
|
0 |
1 |
1 |
|
30. |
A |
2 |
4 |
6 |
, |
B |
2 |
5 |
0 . |
|
|
1 |
2 |
1 |
|
1 |
1 |
2 |
|
§3. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Пример 1.3.
Проверить совместность системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) с помощью обратной матрицы; в) методом Гаусса.
x 2 y 3z 0, 2x y 4z 5, 3x y z 2.
Решение:
Дана система линейных неоднородных алгебраических уравнений. Совместность данной системы проверим по теореме
19
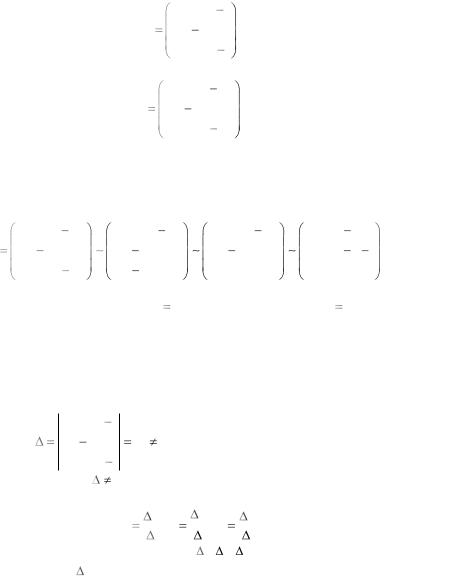
Кронекера-Капелли. С помощью элементарных преобразований найдем ранг матрицы
1 |
2 |
3 |
A 2 |
1 |
4 |
3 |
1 |
1 |
данной системы и ранг расширенной матрицы
|
1 |
2 |
3 |
0 |
B |
2 |
1 |
4 |
5 . |
|
3 |
1 |
1 |
2 |
Для этого умножим первую строку матрицы B на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей.
Далее из второй строки вычтем третью, в результате в
полученной матрице вторую строку сократим на (-5): |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
1 |
2 |
3 |
0 |
B |
2 |
1 |
4 |
5 |
0 |
5 |
10 |
5 |
0 |
5 |
10 |
5 |
0 |
1 |
2 |
1 |
|
3 |
1 |
1 |
2 |
0 |
5 |
8 |
2 |
0 |
0 |
2 |
3 |
0 |
0 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ранг матрицы в ее ступенчатом виде равен числу ненулевых
строк. Ранг матрицы A rangA |
3 и ранг матрицы B rangB 3 . |
Так как ранги матриц |
A и B одинаковы и равны количеству |
неизвестных, то данная система совместна и имеет единственное решение.
а) Решим систему линейных уравнений по формулам Крамера. Вычислим главный определитель системы, составленный из
коэффициентов при неизвестных системы:
1 2 3
2 1 4 10 0 .
3 1 1
Так как 0 , то система имеет единственное решение, которое может быть найдено по формулам Крамера:
|
x |
x |
, y |
y |
, z |
|
z |
, |
|
|
|
|
|
||||
где вспомогательные определители |
x , |
y , z |
получаются из главного |
|||||
определителя |
путем |
замены |
соответственно 1-го, 2-го, 3-го |
|||||
столбцов столбцом свободных членов.
Вычислим вспомогательные определители:
20

|
0 |
2 |
3 |
|
|
|
|
|
|
1 |
0 |
3 |
|
|
|
|
1 |
2 |
0 |
|
||||
x |
5 |
1 |
4 |
|
5; |
|
y |
|
2 |
5 |
4 |
|
20; |
z |
2 |
1 |
5 |
15 . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
1 |
1 |
|
|
|
|
|
|
3 |
2 |
1 |
|
|
|
|
3 |
1 |
2 |
|
||||
|
|
По формулам Крамера имеем: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
x |
|
5 |
|
1 |
; y |
|
20 |
|
2; z |
15 |
|
3 |
. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
10 |
2 |
10 |
|
10 |
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Ответ: x |
|
1 |
; y |
2; z |
3 |
. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б) Рассмотрим матричный метод решения данной системы линейных уравнений:
x 2 y 3z 0; 2x y 4z 5; 3x y z 2.
Решение:
Имеем: |
|
|
|
|
|
1 |
2 |
3 |
0 |
|
x |
A 2 |
1 |
4 ; B |
5 |
; X |
y |
3 |
1 |
1 |
2 |
|
z |
|
|
|
Запишем данную систему в матричной форме: |
|||||||||
|
|
|
|
|
|
|
|
|
A X |
B. |
|
|
Если |
|
матрица |
|
A |
- |
невырожденная, |
т.е. определитель системы |
|||||
|
A |
|
0 , то, |
умножая обе части матричного уравнения A X B на |
||||||||
|
|
|||||||||||
матрицу A 1 слева, получаем решение системы в матричной форме: |
||||||||||||
|
|
|
|
|
|
|
|
|
X |
A 1 |
B . |
|
Вычислим |
A |
|
10 |
0 (смотри вычисление случай а)). |
||||||||
Матрица невырожденная и искомое решение имеет вид: |
||||||||||||
x |
0 |
|
|
|
1 |
A11 |
A21 |
A31 |
|
|||
y |
|
A 1 5 , где A 1 |
A |
A |
A |
- обратная матрица. |
||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
12 |
22 |
32 |
|
z |
2 |
|
|
|
|
|
A13 |
A23 |
A33 |
|
||
Обратная матрица существует, т.к. |
10 |
0 . Найдем ее. |
||||||||||
21
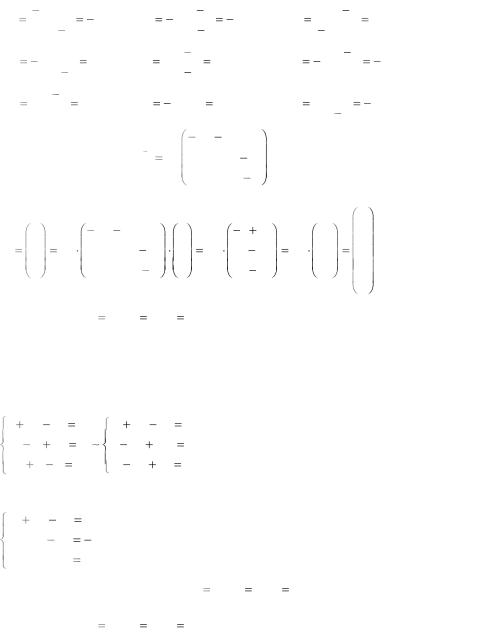
A11 |
1 |
4 |
|
3; |
|
|
A21 |
|
|
|
2 |
|
|
|
|
3 |
|
|
1; |
|
A31 |
|
2 |
3 |
5; |
|||||||||||
1 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A12 |
|
4 |
|
14; |
|
|
A22 |
|
1 |
|
|
|
3 |
|
|
8; |
|
|
A32 |
|
|
1 |
3 |
|
10; |
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
3 |
1 |
|
|
|
3 |
|
|
|
1 |
|
|
|
|
|
|
2 |
4 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
A13 |
|
|
1 |
|
|
5; |
|
|
A23 |
|
|
1 |
2 |
|
5; |
|
|
A33 |
|
1 |
|
2 |
|
5. |
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
1 |
|
|
|
|
|
|
3 |
1 |
|
|
|
|
2 |
|
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 |
1 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
A 1 |
|
14 |
8 |
10 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
3 |
|
1 |
5 |
0 |
|
|
|
|
|
|
|
|
5 |
10 |
|
|
|
5 |
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
X |
y |
|
14 |
|
8 |
10 |
5 |
|
|
|
|
|
10 |
20 |
|
20 |
|
|
2 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
10 |
|
|
|
|
|
|
10 |
|
10 |
|
|
|
||||||||||||||||||||||||
|
z |
|
5 |
|
5 |
5 |
2 |
|
|
|
|
|
25 |
10 |
|
15 |
|
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
Ответ: x |
1 |
; |
y 2; |
|
z |
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) Решим систему методом Гаусса. Исключим x |
из второго и третьего |
|||||||||||||||||||||||||||||||||||
уравнений. Для этого первое уравнение умножим на (-2) и сложим со вторым, затем первое уравнение умножим на (-3) и сложим с третьим уравнением:
x 2 y 3z 0, |
x 2 y 3z 0, |
2x y 4z 5, |
5y 10z 5, |
3x y z 2, |
5y 8z 2. |
Далее из второго уравнения вычтем третье, и затем все коэффициенты разделим на (-5), получим:
x 2 y 3z 0,
y 2z |
1, |
|
|
|
|
|
|
|
|
|
2z |
3. |
|
|
|
|
|
|
|
|
|
Из полученной системы находим |
x |
1 |
; y 2; z |
3 |
. |
|||||
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
Ответ: |
x |
1 |
; y 2; z |
3 |
. |
|
|
|
|
|
2 |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
22
