Лекція 6 . Кінематичний аналіз пр. Розв’язання прямої задачі кінематики

У кінематичному аналізі розрізняють пряму й зворотну задачі.

Пряма задача – полягає у визначенні за заданими узагальненим координатами маніпулятора положення його робочого органу або будь-якої іншої ланки. Необхідність розв’язання прямої задачі зумовлена неможливістю прямого вимірювання координат захвату, у той час як поточне значення кожної із узагальнених координат маніпулятора вимірюються відповідними датчиками.

Зворотна задача полягає у визначенні узагальнених координат маніпулятора, що відповідають заданому положенню захвату або іншої ланки. Необхідність розв’язання зворотної задачі зумовлена тим, що планування траєкторії руху маніпулятора проводиться у декартовій системі координат, зв’язаній із основою робота, а приводи ступенів рухомості діють безпосередньо на узагальнені координати.

Узагальненими, або лагранжевими координатами цієї механічної системи називаються такі незалежні один від одного параметри, за допомогою яких можна в будь-який момент визначити положення цієї системи і, отже, виразити декартові координати в усіх її точок через ці параметри. Кількість узагальнених координат визначає число ступенів свободи цієї системи.

Розв’язаня прямої задачі

Розглянемо розв’язання прямої задачі, виділивши три етапи розв’язання:

• визначення рівнянь зв’язку положення робочого органу маніпулятора з величинами узагальнених координат;

• визначення швидкості руху робочого органу як функції узагальнених координат і їх швидкостей;

• знаходження прискорення робочого органу як функції узагальнених координат, їх швидкостей та прискорень.

Для розв’язання прямої задачі зв’яжемо з основою робота систему координат 0₀x₀y₀z₀, котра збігається з абсолютною системою, якщо основа нерухома, як на рисунку.1.; з першою ланкою систему 0xyz, положення якої визначається координатою першої ступеня рухомості; із другою – 0₁x₁y₁z₁, положення якої відносно 0xyz, визначається другим ступенем рухомості і т.д.

Якщо деяку точку С у системі координат, зв’язаній з (і + 1)–ою ланкою, представити у вигляді радіус–вектора С_і+1, то між цим вектором та вектором С_і, що являє собою цю точку у системі координат, зв’язаній з і-тою ланкою, існує зв’язок

С_і = Т_(і+1)іС_і+1,

де Т_(і+1)і – матриця перетворень координат із системи 0_i+1x_i+1y_i+1z_i+1 до системи 0_ix_iy_iz_i.

Рис.6.1. Координатні осі ПР, що працює в циліндричній системі координат

Матриці перетворення для рухів кінематичних пар V класу можуть бути записані в такому виді:

• для обертання навколо осі 0х: ;

• для обертання навколо осі 0у: ;

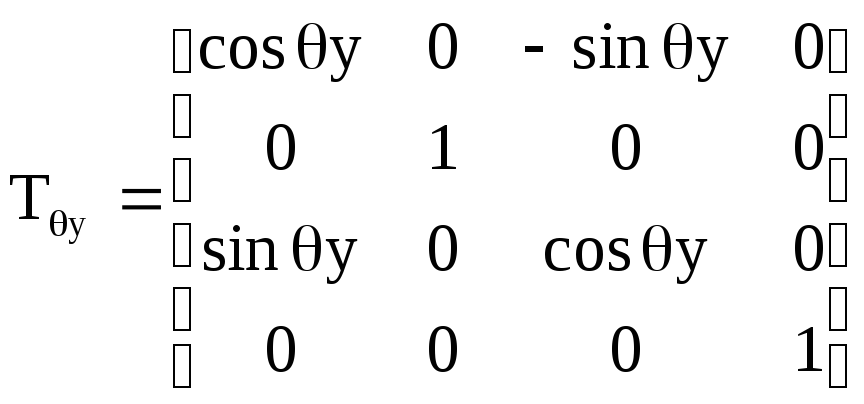• для обертання навколо осі 0z: ;

• для лінійного переміщення вздовж осі 0х: ;

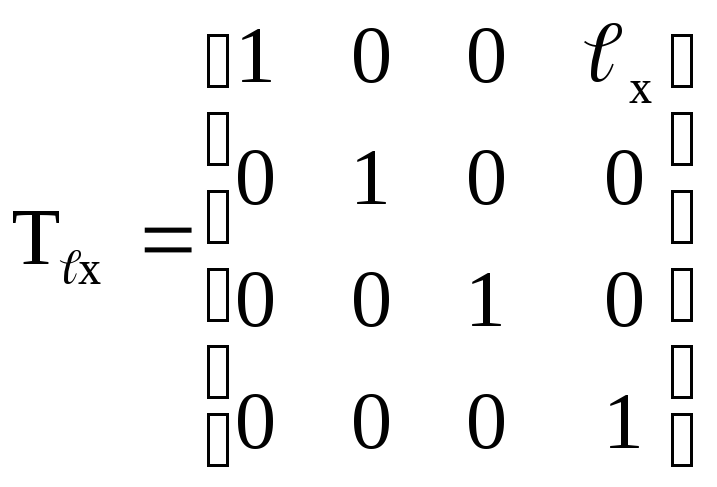• для лінійного переміщення вздовж осі 0у: ;

• для лінійного переміщення вздовж осі 0z: .

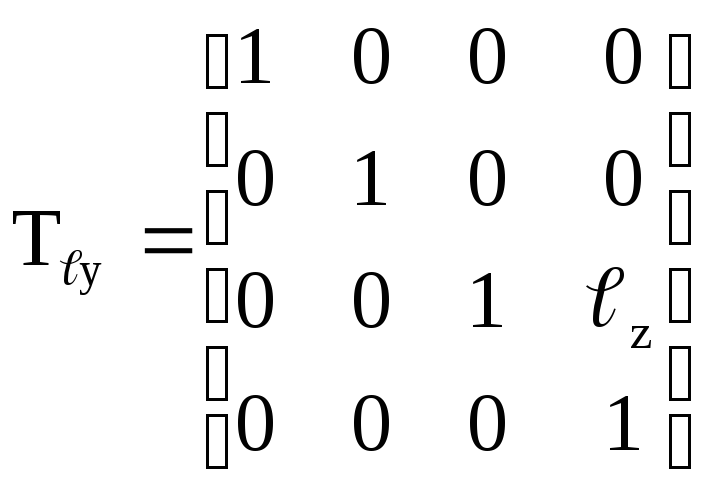Знаючи положення робочого органу С_nу системі координат 0_nx_ny_nz_n, що зв’язана з ним, можна знайти його положення С₀ у абсолютній системі координат, яка зв’язана з основою робота або прив’язана до цехової системи координат за допомогою перетворення:

С₀ = Т₁₀Т₂₁…T_n(n–1)С_n

Для будь-якої точки, заданої у і-й системі координат радіус-вектором R_і, цей вираз можна переписати у вигляді

R₀ = Г_іR_і,

де Г_і – Т₁₀Т₂₁…Т_і(і–1) – матриця перетворення і-тої ланки, що описує її положення у системі координат 0₀x₀y₀z₀.