Кут. Прямий кут
Отримання геометричної фігури
В процесі роботи з багатокутниками учні отримають перші відомості про кути (кут створюють дві сторони багатокутника, які виходять з однієї вершини),й вчаться показувати кути багатокутника. З цією метою виконуються вправи: паперовий багатокутник розривається на частини так, щоб кожна з них містила по 1 вершині та по 2 сторони (частини сторін),які виходять з цієї вершини; звертається увага дітей на те що вершина багатокутника є й вершиною відповідного кута. Спочатку знайомимо дітей з паперовими моделями кутів. Діти повинні виготовити їх, розірвавши паперовий багатокутник.
Ілюстрація: кут столу, дошки та ін.
Властивості:величина кута не залежить від довжини його сторін, а залежить від взаємного розташування його сторін.
Виділення фігури, що вивчається, із множини інших фігур: тут ми показуємо кути багатокутників.
Побудова геометричної фігури: ставимо крапку – це вершина кута й креслимо два промені, які мають спільний початок (цю точку) – це сторони кута.
Після цього показуємо отримання прямого кута перегинанням аркушу паперу “неозначеної” форми:
Учні беруть аркуш паперу й складають його удвічі, лінія згину розгладжується, аркуш розгортається; діти впевнюються, що лінія згину – пряма. Ще раз по лінії згину перегинаємо аркуш – отримаємо модель прямого кута. Розгортаємо аркуш й показуємо учням, що дві лінії, що перетинаються ділять аркуш на 4 частини – на 4 кути. Вершина цих кутів – 1 крапка. Всі ці кути рівні(порівнюємо кути, які отримано різними учнями). Ці кути називаються прямими.
Після цього порівнюємо непрямі та прямі кути з моделлю прямого кута. При накладенні звертаємо увагу, щоб вершини і одна із сторін обох кутів збігалися.
У подальшому для встановлення виду кута використовують прямий кут креслярського трикутника, якщо кути збігаються (тобто збігаються їх сторони і вершини), тоді цей кут є прямим, якщо ні – не прямий.
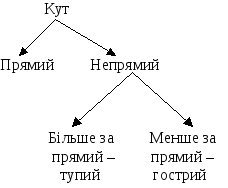
Для закріплення уявлень про прямий кут пропонуємо вправи:
1) серед даних кутів знайти прямі кути:
2) у даних багатокутників знайти прямі кути:
3) накреслити прямий кут у зошиті, використовуючи розліновку зошиту.
4) накреслити трикутник (чотирикутник),який має прямий кут.
Доцільно поряд з паперовими моделями кута використовувати модель “розсувного кута” – малку, Її можливо виготовити із двох паличок, що скріплені гвіздком. За допомогою такої моделі діти наочно впевнюються що величина кута залежить не від довжини його сторін, а від взаємного розташування сторін відносно одне одного.
Поняття кута закріпляється при розгляданні прямокутника. Поняття “прямокутник” та “квадрат” розглядаються за планом:
пропонуємо набір геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються;
вводимо означення фігури;
ілюстрація;
властивості;
задачі на побудову.
Прямокутник
Пропонуємо набір геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються.
Уважно розгляньте фігури. Яку фігуру можна виключити? Чому?
Як одним словом можна назвати решту фігур? (чотирикутники)
Знайдіть чотирикутник, у якого немає прямого кута (за допомогою креслювального трикутника). (2, 3)
Знайдіть чотирикутник, у якого є тільки один прямий кут (1). Виключимо його, що можна сказати про решту чотирикутників? (в цих чотирикутниках більш ніж один прямий кут).
Знайдіть чотирикутник, у якого тільки два прямих кута (4). Виключимо його, що можна сказати про решту чотирикутників?(в цих чотирикутниках більш ніж два прямих кута).
Що можна сказати про решту чотирикутників? (5, 6, 7) Скільки в них прямих кутів? (в них всі кути прямі!)
Такі фігури називаються прямокутниками.
Вводимо означення фігури: (родове поняття – чотирикутник, видове поняття – прямі кути)
Означення: чотирикутник, у якого всі кути прямі називається прямокутником.
Ілюстрація: знайдіть у оточуючій обстановці предмети прямокутної форми.
Покажіть прямокутники серед геометричних фігур.
Виріжте з паперу в клітинку прямокутник.
Властивості:Дітям пропонується набір геометричних фігур, які вирізані з аркушу:
Візьміть в руки прямокутник. Порівняйте за довжиною його протилежні сторони – ті, що лежать напроти одна одної. Використовуйте прийом накладання.
Що цікавого ви помітили? (у прямокутника протилежні сторони попарно рівні).
Перевіримо це ствердження таким чином: виміряйте та запишіть довжину кожної сторони синього прямокутника (у кожного учня різні сині прямокутники).
Назвіть отримані результати вимірювання (вчитель їх записує на дошці)Уважно подивіться на результати вимірювання. Який можна зробити висновок? (у прямокутника протилежні сторони рівні)
Візьміть червоний прямокутник (червоні прямокутники – різні квадрати).Виміряйте довжину його сторін й назвіть отримані результати (вчитель записує їх на дошці).
Що цікавого ви помітили? (є такі прямокутники, у котрих не тільки по дві протилежні сторони рівні, а ще є й такі, у яких всі сторони рівні, але взагалі про них теж можна сказати, що в них протилежні сторони рівні.)
Задачі на побудову.