Порівняння математичних виразів

В 2-му класі продовжується робота над порівнянням чисел, числа та виразу, двох математичних виразів.

Порівняти математичні вирази – це означає встановити, значення якого виразу більше, менше або вони рівні.

Вирази порівнюються декількома способами:

1. Знаходимо значення кожного виразу і порівнюємо отримані числа. Більше той вираз, значення якого більше. І навпаки.

2. Порівнюємо вирази, аналізуючи їх: 35 …34 - обидва вирази – добутки; в обох добутках однакові перші множники, значить більший той вираз у якого другий множник більший: 5 більш ніж 4,тому 35 більше 34.

3. Перетворення виразу й порівняння виразів 2-им способом: 34 + 3 > 34.

Розглянемо ці способи докладно.

Спочатку учні вчаться порівнювати вираз і число, наприклад: 8 + 5 і 12. Першим кроком знаходимо значення суми: 8 + 5 = 13. Другим кроком порівнюємо отриманий результат з числом 12 : 13 > 12. Третім кроком робимо висновок: якщо 13 > 12, то 8 + 5 > 12. Форма запису в зошиті:

Далі порівнюються два математичні вирази. Треба порівняти вирази 45 – 6 і 28 + 4. Міркуємо так:

1. знаходимо значення першого виразу: 45 – 6 = 39;

2. знаходимо значення другого виразу: 28 + 4 = 32;

3. порівнюємо отримані результати: 39 > 32;

4. робимо висновок: так як 39 > 32, то й 45 – 6 > 28 + 4.

Форма запису в зошиті:

Розглянемо другий спосіб порівняння математичних виразів – логічний. Зазначимо, що цей спосіб порівняння математичних виразів був нами запропонований учням ще в 1-му класі.

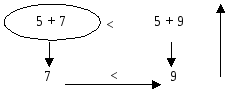
• Прочитайте кожний вираз.

5 + 7 – сума чисел 5 та 7;

5 + 9 – сума чисел 5 та 9.

• Чим цікаві ці вирази? (Обидва вирази – це суми.)

• Що спільного в цих сумах? (В них однакові перші доданки)

• Чим вони відрізняються? (В них різні другі доданки).

• Зробіть висновок: з двох сум з однаковими першими доданками, менша та, в якій другий доданок менший.

Порівнюючи математичні вирази логічним способом ми застосовуємо знання учнів про зміну результатів арифметичних дій в залежності від зміни компонентів. Вчитель повинен пам’ятати, що змінюються в одному напрямку: якщо один іззбільшиться, то йтеж збільшиться, і навпаки. Так само в одному напрямі змінюютьсяв залежності від зміни. Алезмінюються в зворотному напрямі від зміни: якщозбільшиться, то, навпаки зменшиться.

Наприклад:

(Чим більше відняли від одного й того самого числа, тим менше залишилося)

З двох часток з однаковими дільниками менша та, у якій ділене менше.

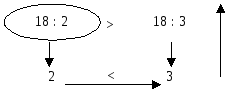
З двох часток з однаковими діленими більше та, в якій дільник менший.

Можна пропонувати дітям завдання на порівняння математичних виразів двома способами. Наприклад:

2 5 > 2  2 2  5 > 2  2

10 > 4 5 > 2 (якщо перші множники однакові, то більший той добуток, у якого другий множник більший)

В темі “Табличне множення і ділення” учні знайомляться з третім способом порівняння математичних виразів на підставі перетворення математичного виразу. Наприклад:

2 + 2 + 2 + 2 < 2  5

2  4 < 2  5

Порівнюючи математичні вирази даним способом, ми спочатку виконали тотожне перетворення першого виразу на підставі конкретного змісту дії множення.