- •Лекція №1.Означення диференціального рівняння і розв’язку. Задача Коші. Теорема існування та єдиності розв’язку задачі Коші
- •1.Означення диференціального рівняння і розв’язку.
- •2.Геометрична інтерпретація, диференціального рівняння першого порядку.
- •3. Загальні рішення диференціального рівняння. Задача Коші.
- •Лекція №2. Рівняння з розділеними змінними. Однорідні рівняння
- •1. Рівняння з розділеними змінними.
- •2. Рівняння, що приводяться до рівнянь із розділеними змінними.
- •3.Однорідні рівняння
- •4. Рівняння, що приводяться до однорідних рівнянь.
- •Практичне заняття №1. Рівняння з розділеними змінними
- •Практичне заняття №2. Однорідні рівняння
- •Лекція №3. Лінійні рівняння першого порядку. Рівняння Бернуллі та Рікатті-Буля
- •1. Лінійні рівняння першого порядку.
- •2. Рівняння Бернуллі.
- •3. Рівняння Рікатті – Буля.
- •4.Рівняння в повних диференціалах.
- •Практичне заняття №3.Лінійні рівняння першого порядку. Рівняння Бернуллі
- •Лекція №4.Особливі точки. Особливі рішення. Рівняння Клеро
- •2. Огибаюча сімейства кривих. Рівняння Клеро.
- •Практичне заняття №4. Рівняння Клеро
- •Лекція №5. Системи диференціальних рівнянь першого порядку. Теорема існування та єдиності розв’язку задачі Коші. Рівняння п-го порядку
- •1. Системи диференціальних рівнянь. Теорема існування та єдиності.
- •2. Рівняння n-го порядку.
- •3. Загальні способи зниження порядку рівняння
- •Практичне заняття №5. Рівняння п-го порядка. Способи зниження порядка
- •Лекція №6. Лінійні рівняння n-го порядку. Системи лінійно незалежних функцій
- •1. Лінійні та однорідні рівняння n-го порядку.
- •2. Системи лінійно незалежних функцій.
- •Лекція №7. Формула Остроградського – Ліувілля. Лінійні однорідні рівняння з постійними коефіцієнтами
- •1. Формула Остроградського – Ліувілля та її застосування для розв’язку рівняння другого порядка.
- •Практичне заняття №6. Лінійне однорідне рівняння. Формула Остроградського – Ліувілля. Лінійні однорідні рівняння з постійними коефіцієнтами
- •Лекція №8. Лінійні неоднорідні рівняння n - го порядку. Застосування рівнянь у теорії коливань. Резонанс
- •1. Загальний вигляд рішення лінійного неоднорідного рівняння.
- •2. Метод невизначених коефіцієнтів.
- •3. Знаходження рішення неоднорідного лінійного рівняння з постійними коефіцієнтами для спеціальної правої частини.
- •4.Застосування рівнянь у теорії коливань. Резонанс.
- •Практичне заняття №7. Неоднорідні лінійні рівняння
- •Лекція №9. Системи п звичайних диференційних рівнянь. Лінійні рівняння з частинними похідними першого порядку
- •1. Системи звичайних диференційних рівнянь
- •2. Лінійні рівняння з частинними похідними.
- •3.Загальний випадок лінійного рівняння.
- •Практичне заняття №8. Система диференційних рівнянь. Диференційні рівняння у частинних похідних першого порядку
- •2. Рівняння у частинних похідних першого порядку. Означення. Розв’язок.
- •Лекція №10. Класифікація рівнянь у частинних похідних другого порядку. Диференційні рівняння з двома змінними
- •1.Визначення рівняння другого порядку з двома змінними у частинних похідних.
- •2.Класифікація рівнянь.
- •Лекція №11. Рівняння гіперболічного типу. Постановка крайової задачі. Теорема єдиності розв’язку
- •1. Постановка крайової задачі.
- •Лекція №12. Редукція, загальної задачі. Задачі на прямій і напівпрямій. Формула Даламбера, метод продовження
- •1.Редукція, загальної задачі.
- •2. Формула Даламбера.
- •3. Крайова задача для напівпрямої, і метод продовжень.
- •Практичне заняття №9. Типи рівнянь другого порядку у частинних похідних. Рівняння коливання струни. Формула Даламбера
- •Лекція №13. Неоднорідні гіперболічні, рівняння на прямій і піввісі. Метод Фур’є розділення змінних
- •1. Неоднорідні гіперболічні рівняння на прямій і піввісі.
- •2. Метод розділення змінних.
- •Лекція №14. Перша крайова задача для гіперболічного рівняння
- •1.Неоднорідне рівняння з нульовими граничними умовами.
- •2.Перша крайова задача.
- •Практичне заняття №10. Метод Фур’є. Гіперболічні рівняння
- •3. Розв’язання першої крайової задачі у загальному випадку.
- •Лекція №15. Рівняння параболічного типу
- •1.Постанова крайових задач.
- •2. Єдиність розв’язку.
- •3. Метод розділення змінних.
- •Лекція №16. Перша крайова задача для рівняння параболічного виду
- •1. Неоднорідна задача з нульовими початковими і граничними умовами.
- •2. Перша крайова задача.
- •3. Задачі на нескінченій та напівнескінечній прямій.
- •Лекція №17. Рівняння еліптичного типу
- •1. Постановка крайових задач.
- •2. Перша крайова задача для круга. Інтеграл Пуассона.
- •3. Частинний розв’язок рівняння Лапласа.
- •Практичне заняття №11. Параболічні та еліптичні рівняння
- •Література:
3.Загальний випадок лінійного рівняння.
В розглянутому рівнянні φ не входить в Хі і права частина дорівнювала 0.
Розглянемо
рівняння![]()
де Yі містить х1,х2,…,хп,φ. Будемо шукати сімейство розв’язків у вигляді неявної функції w(x1,…,xn,φ)=c.
Згідно
з диференціювання неявної функції
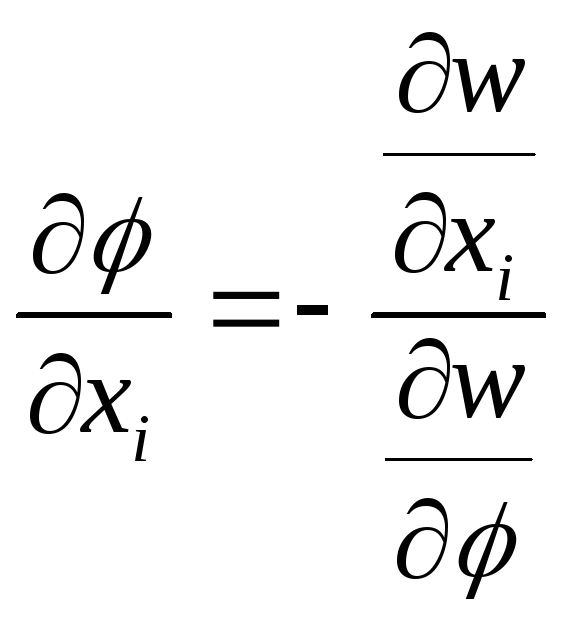 підставивши в рівняння отримаємо
підставивши в рівняння отримаємо![]() котре має вид розглянутий вище.
котре має вид розглянутий вище.
В
силу довільних
![]() змінніх1,…,хп,φ
можуть мати будь-які значення і
останнє
рівняння має тотожно виконуватись
відносно х1,…,хп,φ.
Якщо w
знайдено, то рівняння w(х1,…,хп,φ)=0
визначає
φ.
змінніх1,…,хп,φ
можуть мати будь-які значення і
останнє
рівняння має тотожно виконуватись
відносно х1,…,хп,φ.
Якщо w
знайдено, то рівняння w(х1,…,хп,φ)=0
визначає
φ.
Приклад.
![]()
Розглянемо w(x,y,φ)=c. Відносно w рівняння прийме вигляд
![]() .
.
Тоді,
з попереднього приклада маємо w(x,y,φ)=![]() ,
де F
– довільна функція. Рівність
,
де F
– довільна функція. Рівність
![]() визначаєφ(x,y).
визначаєφ(x,y).
Практичне заняття №8. Система диференційних рівнянь. Диференційні рівняння у частинних похідних першого порядку
Необхідні відомості: 1. Означення розв’язку та загального інтеграла системи рівнянь.
2. Рівняння у частинних похідних першого порядку. Означення. Розв’язок.
Задачі.
1.1
а)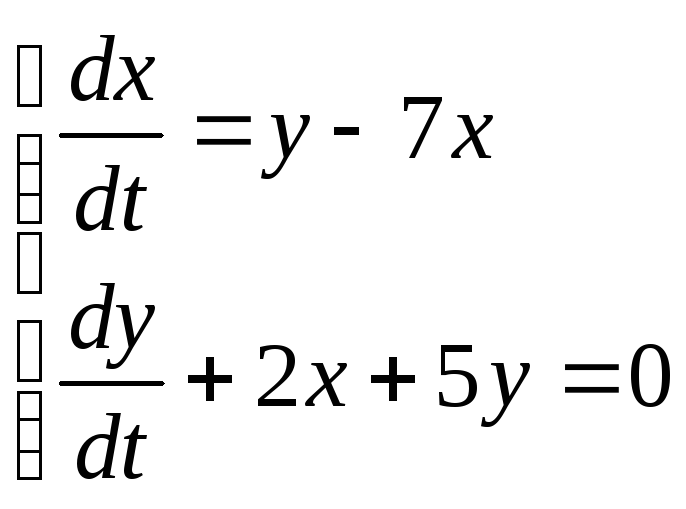 Розв’язати за допомогою метода
виключення.
Розв’язати за допомогою метода
виключення.
б)
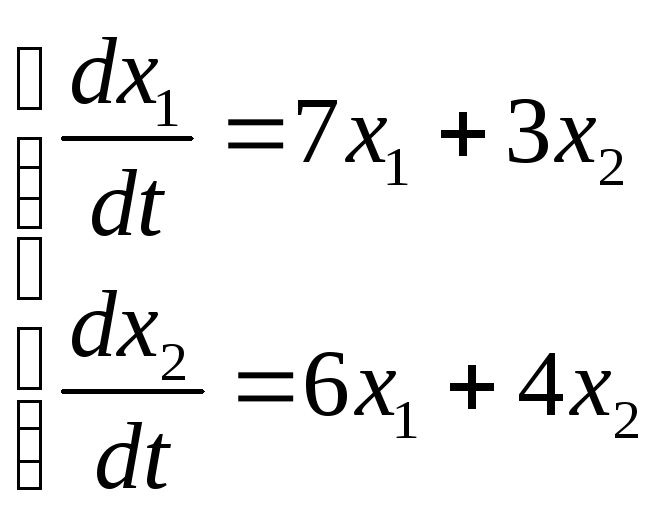 Розв’язати
допомогою матриць.
Розв’язати
допомогою матриць.
1.2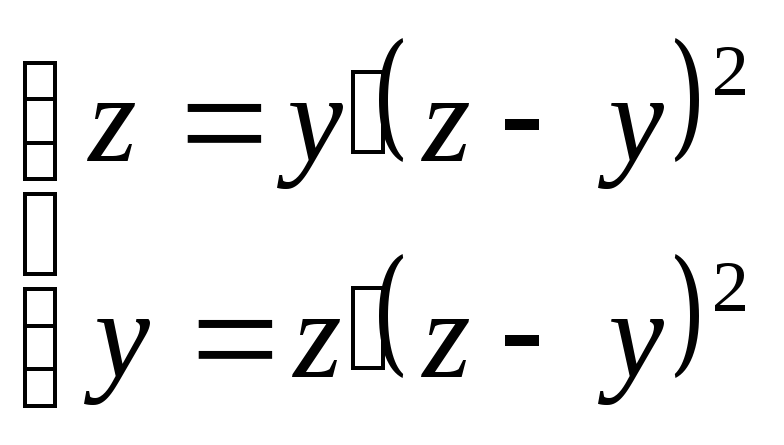
1.3![]()
2.1
![]() .
Знайти загальний інтеграл.
.
Знайти загальний інтеграл.
2.2
Знайти поверхню яка задовольняє рівняння
![]() ,
що проходить через окіл
,
що проходить через окіл
Задачі для самостійної роботи.
Розв’язати методом виключень.
1.
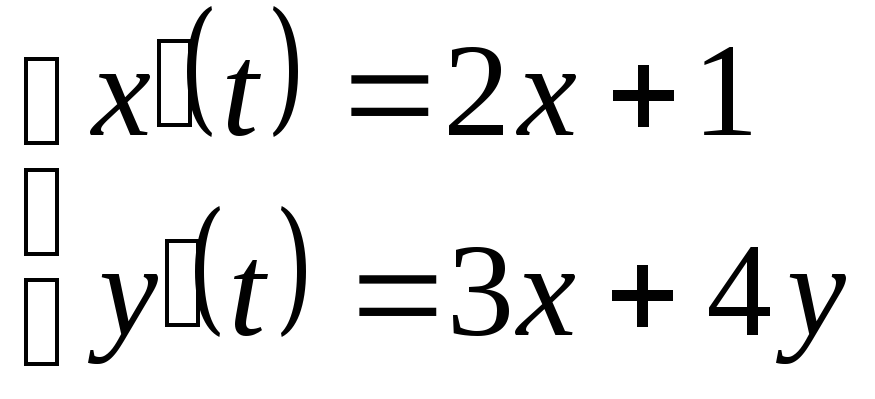 . 2.
. 2.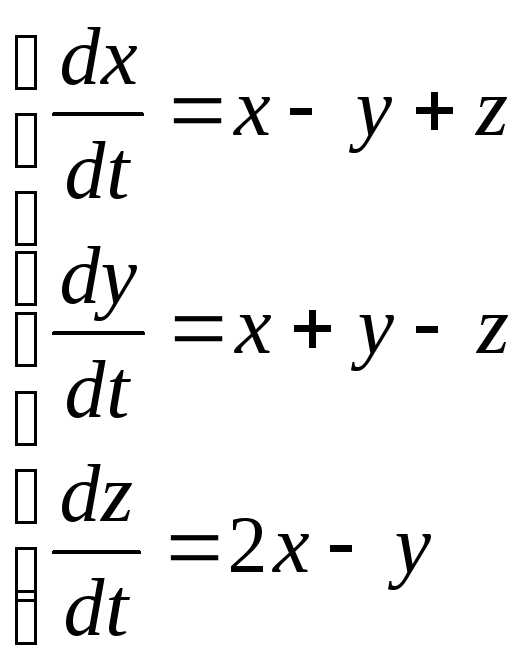 . 3.
. 3.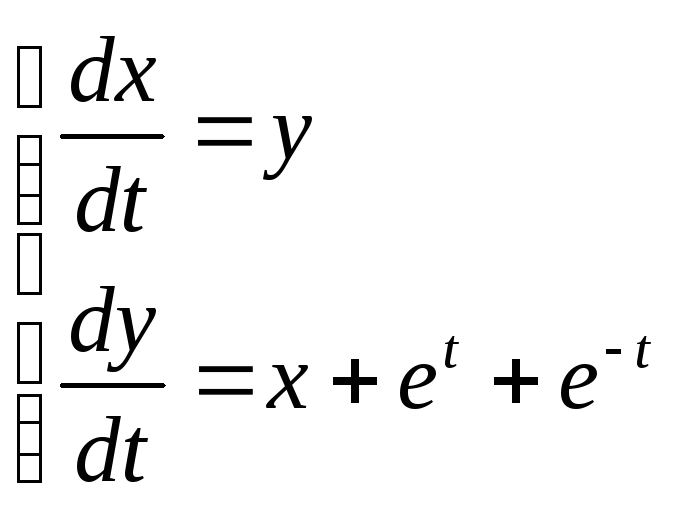 .
.
4.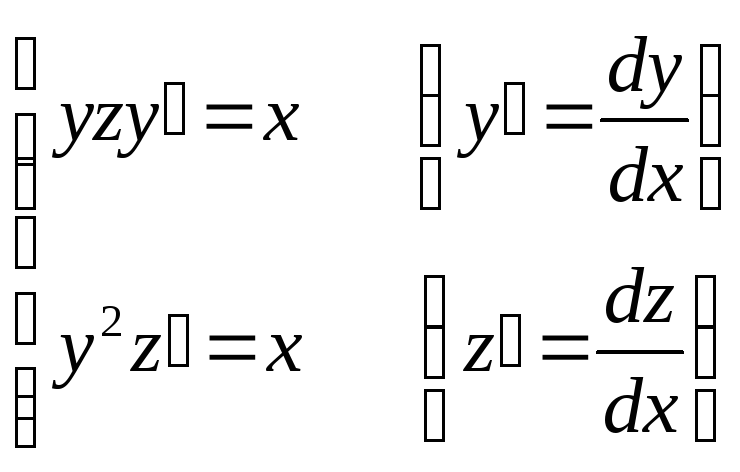 . 5.
. 5.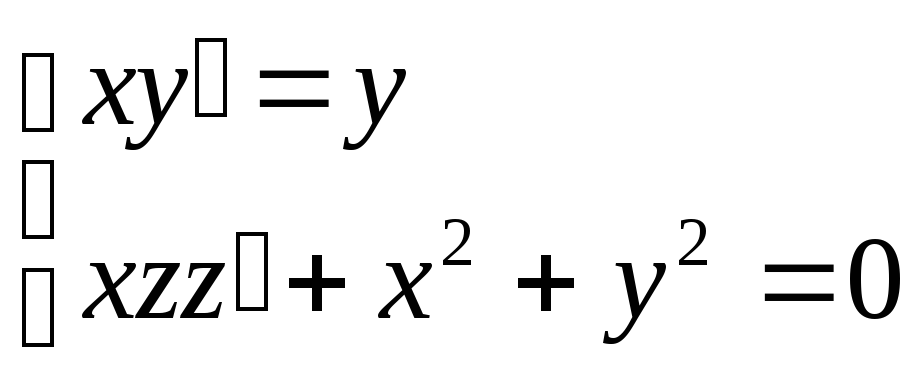 .
6.
.
6.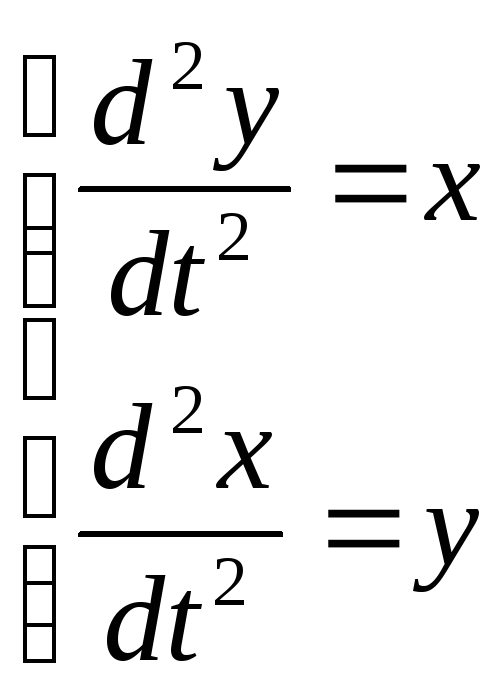 .
.
7.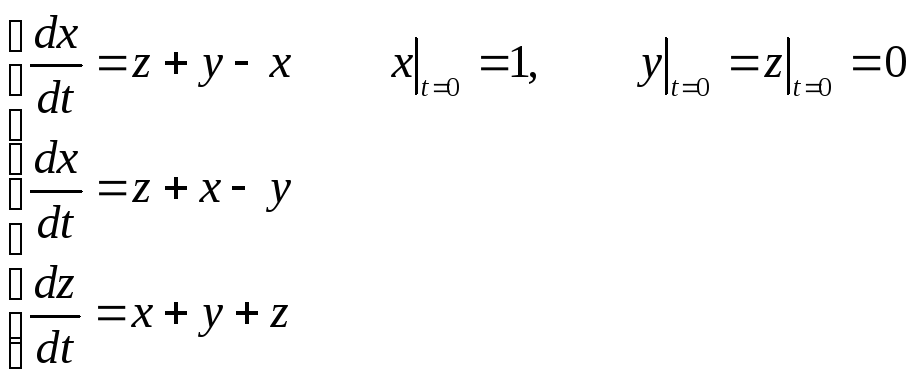 .
.
Розв’язати за допомогою матриць
8.
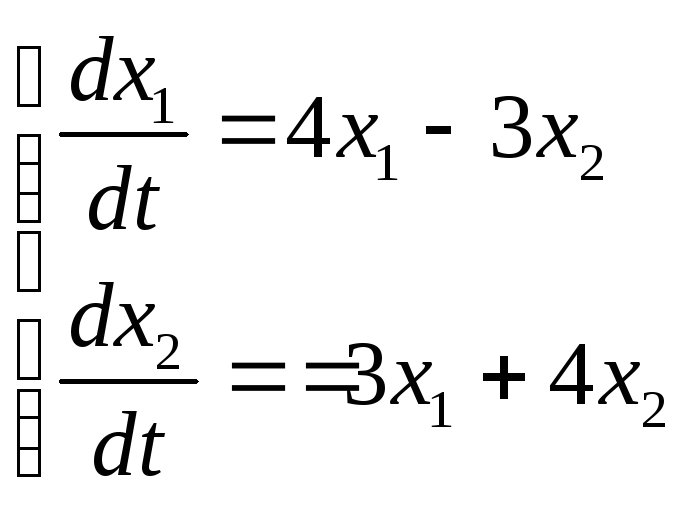 . 9.
. 9.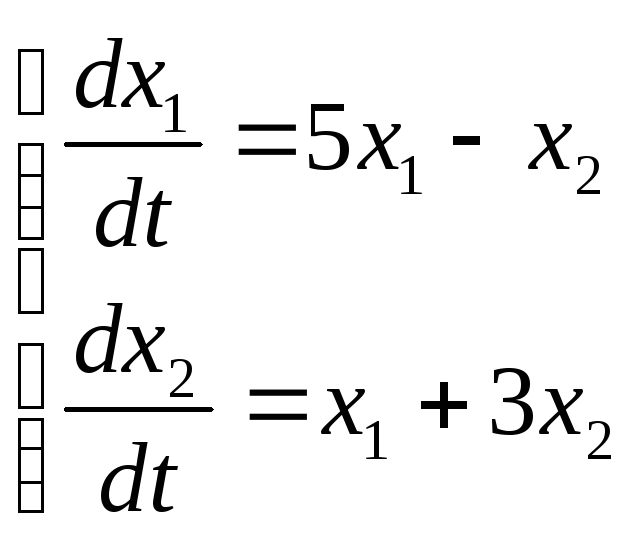 .
10.
.
10.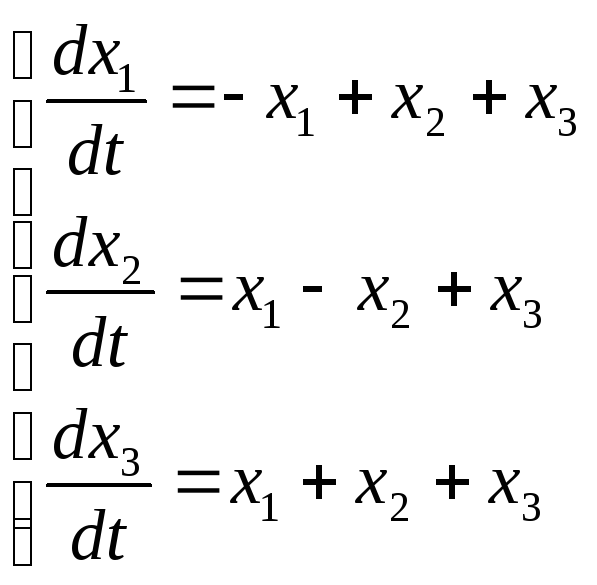 .
.
11.
Знайти загальний інтеграл
![]() .
.
12.
Знайти загальний інтеграл
![]() .
.
13.
Знайти поверхню, що задовольняє рівняння
![]() та проходить через параболу
та проходить через параболу![]() .
.
Лекція №10. Класифікація рівнянь у частинних похідних другого порядку. Диференційні рівняння з двома змінними
1.Визначення рівняння другого порядку з двома змінними у частинних похідних.
Означення.
Співвідношення
![]() ,
дех,
у
незалежні змінні, а и,
,
дех,
у
незалежні змінні, а и,
![]() ,функція
від х,у,
та
її частинні похідні,
називається
рівняння у частинних похідних другого
порядку з двома невідомими.
,функція
від х,у,
та
її частинні похідні,
називається
рівняння у частинних похідних другого
порядку з двома невідомими.
Рівняння називається лінійним відносно старших похідних, якщо воно має вид:
![]() ,
де а11,а21,а22
– функції від х,у.
,
де а11,а21,а22
– функції від х,у.
Рівняння називається лінійним, якщо воно лінійне відносно всіх похідних
![]() ,
,
де коефіцієнти – функції від х,у.
Якщо f(x,y)=0, то рівняння називається однорідним.
2.Класифікація рівнянь.
За допомогою перетворень ξ=φ(х,у) η=ψ(х,у) (що має обернене) ми отримаємо нове рівняння еквівалентне даному. Спробуємо спростити рівняння за допомогою переходу до нових змінних.
Враховуючи що:
ux=u ξ ξx+u η ηx
uy= u ξ ξy+u η ηy
![]()
![]()
uyy – має вигляд uхх при заміні х на у.
Підставивши в рівняння (*), отримаємо:
![]()
![]()
![]()
![]()
при
цьому
![]() як
і
як
і![]() не залежать від других похідних (в
випадках лінійного рівняння воно
залишається лінійним).
не залежать від других похідних (в
випадках лінійного рівняння воно
залишається лінійним).
Виберемо
ξ та η, щоб
![]() .
.
Розглянемо
рівняння з частковими похідними першого
порядку
![]() .
Якщо
.
Якщо![]() - який-небудь розв’язок цього рівняння,
то припускаючи
- який-небудь розв’язок цього рівняння,
то припускаючи![]() отримаємо, що
отримаємо, що![]() ,
тобто спрощене рівняння другого порядку
зв’язано з розв’язком рівняння першого
порядку.
,
тобто спрощене рівняння другого порядку
зв’язано з розв’язком рівняння першого
порядку.
Теорема.
Якщо
![]() розв’язок
рівняння (**)
розв’язок
рівняння (**)![]() ,
то
,
то![]() - загальний інтеграл звичайного
диференційного рівняння
- загальний інтеграл звичайного
диференційного рівняння![]() .
.
Навпаки,
якщо
![]() загальний інтеграл вказаного звичайного
диференційного рівняння, то функція
загальний інтеграл вказаного звичайного
диференційного рівняння, то функція![]() -
розв’язок диференційного рівняння в
часткових похідних першого порядку
(**).
-
розв’язок диференційного рівняння в
часткових похідних першого порядку
(**).
Доведення.
Якщо
![]() - розв’язок рівняння (**), то рівність
являється тотожністю:
- розв’язок рівняння (**), то рівність
являється тотожністю:
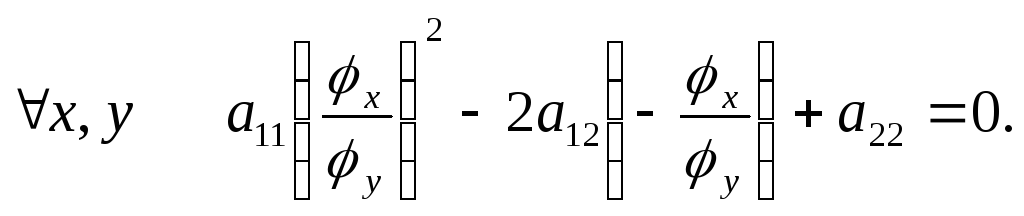
Розглядаючи
співвідношення
![]() маємо,
щоу
– неявно задана функція
маємо,
щоу
– неявно задана функція
![]() і
і![]() .
.
Підставивши в тотожність отримаємо:
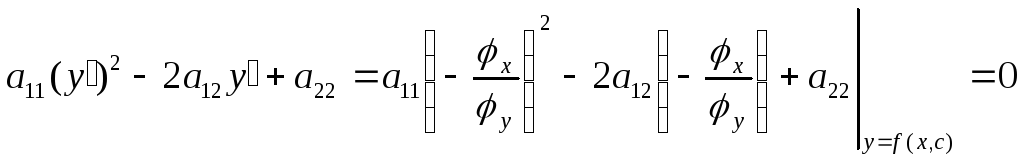 ,
,
тобто
![]() -
загальний інтеграл вказаного звичайного
диференційного рівняння.
-
загальний інтеграл вказаного звичайного
диференційного рівняння.
Нехай
тепер
![]() - загальний інтеграл звичайного
диференційного рівняння. Покажемо, що
- загальний інтеграл звичайного
диференційного рівняння. Покажемо, що![]() .
.
Нехай
![]() яка-небудь
точка. Проведемо через
яка-небудь
точка. Проведемо через![]() інтегральну криву звичайного диференційного
рівняння, припускаючи що
інтегральну криву звичайного диференційного
рівняння, припускаючи що![]() і розглянемо криву
і розглянемо криву![]() .
Для всіх точок цієї кривої
.
Для всіх точок цієї кривої
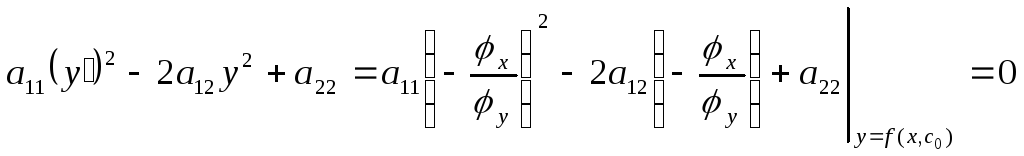 .
.
Припускаючи
що
![]() отримаємо
отримаємо
![]() ,
а оскільки
,
а оскільки
![]() - довільна точка то рівність виконується
для всіх (х,у).
Що і треба було довести.
- довільна точка то рівність виконується
для всіх (х,у).
Що і треба було довести.
Означення.
Рівняння
![]() називається характеристичним для
диференційного рівняння другого порядку
в частинних похідних, а його інтеграли
– характеристиками.
називається характеристичним для
диференційного рівняння другого порядку
в частинних похідних, а його інтеграли
– характеристиками.
Припустимо
![]() (φ – загальний інтеграл характеристичного
рівняння) ми отримаємо, що
(φ – загальний інтеграл характеристичного
рівняння) ми отримаємо, що![]() .
Якщо
.
Якщо![]() являється іншим загальним інтегралом
(незалежним від φ), то припускаючи що
являється іншим загальним інтегралом
(незалежним від φ), то припускаючи що![]() ми
отримаємо, що і
ми
отримаємо, що і![]() .
.
Очевидно, що характеристичне рівняння розпадається на два рівняння
![]() (***)
(***)
![]() .
.
Знак підкорінного виразу визначає тип рівняння
![]() .
.
1.
Якщо
![]() в точці М(х,у),
то рівняння називається рівнянням
гіперболічного типу.
в точці М(х,у),
то рівняння називається рівнянням
гіперболічного типу.
2.
Якщо
![]() в
точці М(х,у),
то рівняння називається рівнянням
еліптичного типу.
в
точці М(х,у),
то рівняння називається рівнянням
еліптичного типу.
3.
Якщо
![]() в точці М(х,у),
то рівняння називається рівнянням
параболічного типу.
в точці М(х,у),
то рівняння називається рівнянням
параболічного типу.
Розглянемо кожну ситуацію окремо.
1.
![]() ,
тоді праві частини (***) дійсні і різні.
Розв’язуючи рівняння (***) отримаємо
незалежні загальні інтеграли
,
тоді праві частини (***) дійсні і різні.
Розв’язуючи рівняння (***) отримаємо
незалежні загальні інтеграли![]() та
та![]() .
Припускаючи
.
Припускаючи![]()
![]() приводимо рівняння другого порядку до
виду
приводимо рівняння другого порядку до
виду![]() .
.
Припускаючи
![]() ,
де
,
де![]() нові змінні і враховуючи, що
нові змінні і враховуючи, що![]() ,
,![]()
![]() ,
рівняння набуває вигляду
,
рівняння набуває вигляду![]() .
.
2.
![]() ,
тоді рівняння (***) має один розв’язок
,
тоді рівняння (***) має один розв’язок![]() .
Покладемо
.
Покладемо![]() та
та![]() -
довільна функція. Тоді
-
довільна функція. Тоді
![]()
![]() .
.
Таким
чином, рівняння другого порядку прийме
вид
![]() .
.
3.
![]() .
Нехай
.
Нехай![]() - комплексний інтеграл першого рівняння
(***). Тоді
- комплексний інтеграл першого рівняння
(***). Тоді![]() - інтеграл спряженого
рівняння
2 з
(***).
Покладемо
- інтеграл спряженого
рівняння
2 з
(***).
Покладемо
![]()
![]()
тоді
еліптичне рівняння приводяться до того
ж виду що й гіперболічне. Замінимо
![]() тобто
тобто![]() .
Вводячи заміну, отримаємо рівняння
.
Вводячи заміну, отримаємо рівняння![]() .
.
Отже, рівняння другого порядку у частинних похідних з двома змінними (за допомогою заміни незалежних змінних) завжди можна привести до одного з трьох канонічних виглядів:
1.
![]() (гіперболічний
тип)
(гіперболічний
тип)![]() або
або![]()
2.
![]() (еліптичний
тип)
(еліптичний
тип)![]()
3.
![]() (параболічний
тип)
(параболічний
тип)![]()
Зауваження. Подібна класифікація має місце і для рівнянь другого порядку з багатьма змінними.
Приклад.
Привести до канонічного виду
![]() .
.
а11=1,
а12=0,
а22=х
і![]() .
.
1. Якщо х>0 рівняння еліптичне.
2. Якщо х<0 рівняння гіперболічне.
3. Якщо х=0 рівняння параболічне.
1.
х>0,
![]()
![]()
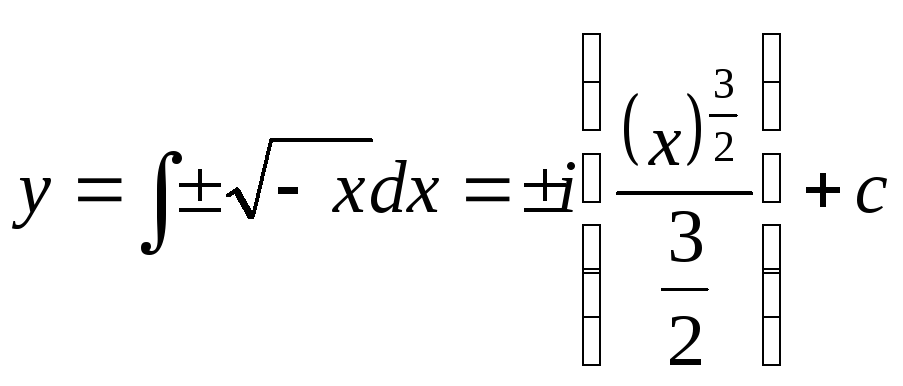 .
Отже
.
Отже
![]()
![]() .
.
Тоді
![]() і
і
![]()
![]()
![]() ,
,
![]()
Підставивши в рівняння отримаємо:
![]() ,
або
,
або
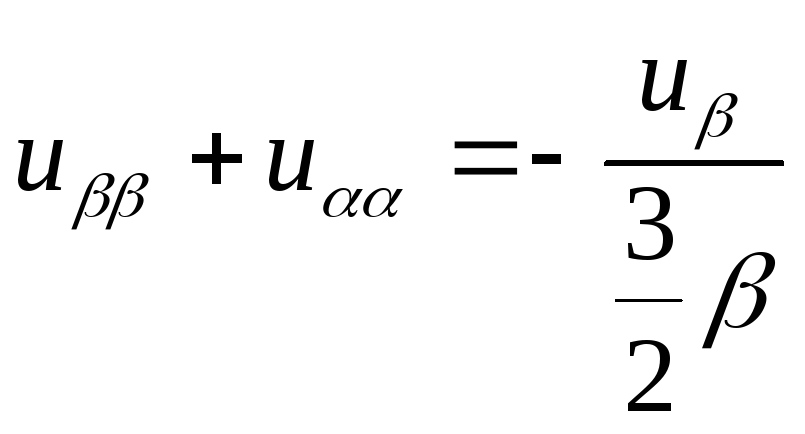 -
еліптичне рівняння
-
еліптичне рівняння
2.
х=0
![]() у=с.
Отже
у=с.
Отже
![]() .
.
Тоді
![]() -
довільна і
-
довільна і
![]() ,
,
![]()
Рівняння прийме вид (після заміни)
![]() (в
х=0),
(в
х=0),
![]() -
параболічне рівняння.
-
параболічне рівняння.
Випадок 3 аналогічний 1.
Зауваження. У випадку постійних коефіцієнтів в лінійному рівнянні
![]()
після
переходу до змінних ξ, η рівняння, якого
б виду воно не було, можна спростити,
звільнившись від похідних першого
порядку, за допомогою заміни
![]() де
де![]() - невизначені коефіцієнти, вибираючи
які відповідним чином, (щоб знищити 2
коефіцієнти), отримаємо рівняння виду:
- невизначені коефіцієнти, вибираючи
які відповідним чином, (щоб знищити 2
коефіцієнти), отримаємо рівняння виду:
![]() (еліптичне)
(еліптичне)
![]() (параболічне)
(параболічне)