02_Молекулярная_физика

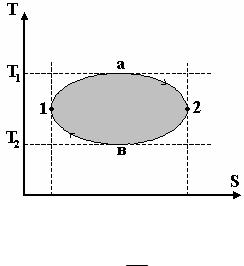
81

Теплообмен в изолированной системе протекает единственным образом: тепло передается от тела с большей температурой к телу с меньшей температурой.

п.2 Максимальный КПД тепловой машины

Рассмотрим цикл в координатах (TS). Разобьем его на участки 12 и 21.

Запишем

dS = dQT , dQ = TdS ,

Q = ∫TdS.

На участке 12 энтропия возрастает, следовательно

Q = ∫2 TdS > 0 ,

1

2

Q1 = ∫TdS ,

1

где Q1 - количество теплоты, полученное рабочим телом. На участке 21 очевидно, что

82

Для увеличения КПД нужно уменьшать Q2 и увеличивать Q1 . Пусть T1 , T2 - температуры нагревателя и холодильника. Величина Q1 численно равна площади, ограниченной кривой 1а2. Чтобы ее увеличить, нужно чтобы участок 1а2 шел по прямой T1 . Величина Q2 численно равна площади под кривой 2в1. Для ее уменьшения необходимо, чтобы график шел по прямой T2 . В результате приходим к циклу: 12341.

Участки 12 и 34 это T1 = const и T2 = const , т.е. изотермическое расширение и сжатие. На участках 23 и 41 имеем

dS = 0 , dQ = TdS = 0 ,

dQ = 0 .

Следовательно, это участки адиабатического расширения и сжатия. График 12341 соответствует циклу Карно. Найдем КПД цикла

Q2 = ∫4 TdS = T2 ∫4 dS = T2 (S4 −S3 )= T2 (S1 −S2 )< 0 ,

Теорема Нернста

Рассмотрим идеальный газ при 0К.

T= 0 ,

ε= 2i kT = 0 .

Все молекулы неподвижны. Каждой молекуле в фазовом пространстве соответствует одна фазовая ячейка, которую данная молекула не может покинуть.

Статистический вес молекулы равен единице

83

Г1 =1.

Статистический вес N молекул

Г = Г1 Г2 Г3 ...ГN =1 1 1...1 =1.

Энтропия системы

S = k lnГ = k ln1 = 0 .

При температуре 0 K энтропия всякой системы равна нулю. Это третье начало термодинамики или теорема Нернста.

84

ГЛАВА 7. ВЕРОЯТНОСТЬ СОСТОЯНИЯ

Математическая вероятность и вероятность состояния

Рассмотрим идеальный газ из N одинаковых молекул, находящихся в объеме V . Разделим этот объем на одинаковые объемы V′.

Обозначим ω′(1) - вероятность того, что одна молекула находится в этом объеме V′. Если все объемы V′ одинаковые, то ω′(1) - вероятность нахождения молекулы в любом объеме V′. Вероятность тог, что молекула находится в одном из объемов V′ равна ω′(1)+ω′(1)+...+ω′(1)= kω′(1),

k = VV′.

На событие, заключающееся в том, что молекула находится в одном из объемов V′, принадлежащих объему V , есть достоверное событие, значит

kω′(1)=1.

Величина в левой части имеет смысл времени, в течение которого N молекул соберутся в одной половине сосуда

t = ∆t ln(1−ωn (N)). ln 1− 21N

Для того чтобы считать такое событие возможным, положим

ωn (N)= 0.9 .

Кроме того, пусть выполняется условие

21N <<1.

Для этого достаточно, чтобы N > 5

ln(1± x)≈ ±x, x <<1,

85

ln 1− 21N ≈ −21N ,

ω′(N)= V′ N .V

Обозначим ω′(N1, N2 )- вероятность того, что N1 молекул находятся в объеме V′, а N2 молекул в остальном объеме (V − V′). Очевидно, что

определенного события. Рассмотрим систему, в которой, например, 4 одинаковые молекулы. Пронумеруем их: 1,2,3,4.… Найдем вероятность того, что в объеме V′- одна любая молекула, а в объеме (V − V′) остальные три.

Проанализируем возможные распределения молекул по объемам V′ и (V −V′). Каждое распределение характеризуется вероятностью ω′(1,3).

Поскольку все молекулы одинаковые, то если рассматривать макросостояние данной системы, то совершенно неважно, какие именно молекулы находятся в объемах V′ и (V −V′).

Таким образом, макросостоянию, которое можно обозначить (1,3) соответствует 4 комбинации, при которых в объемах V′ и (V −V′) находятся 1 и 3 молекулы.

86

Обозначим ω(1,3) - вероятность макросостояния (состояния), при котором

Стирлинга.

lnN!= N lnN .

Запишем

N2 = N − N1 ,

88

Очевидно, что

ωn(0) = ω ω ω...ω = 1− 21N n .

Обозначим ωn(N) - вероятность того, что в опытах в другой половине сосуда находится N молекул.

ωn(N) =1−ωn(0) =1− 1− 21N n ,

1− 21N n =1−ωn (N),

n ln 1− 21N = ln(1−ωn (N)),

n = ln(1−ωn (N)). ln 1− 12N

Пусть каждый опыт продолжается ∆t секунд. Умножим обе части на ∆t ,

∆t n = ln(1−ωn (N)) ∆t . ln 1− 1

2N

89

ГЛАВА 8. ЯВЛЕНИЕ ПЕРЕНОСА В ГАЗАХ

Столкновение молекул

В идеальном газе происходят столкновения между двумя молекулами. Одновременными столкновениями между тремя и большим числом молекул пренебречь.

Молекулы в газе могут сближаться на достаточно малые расстояния, при котором между ними возникают силы отталкивания. Молекулы при этом нужно представлять как упругие сферы радиусами r1 и r2 .

Столкновение молекул возможно только в случае, если центры молекул сблизятся на расстояние равное сумме радиусов (r1 + r2 ).

Минимальное расстояние между центрами двух молекул называется эффективным диаметром молекулы.

Характеристики соударений

Столкновения молекул являются случайными событиями. При столкновении скорость молекулы изменяется случайным образом, как по направления, так и по величине. Следовательно, в общем случае в промежутках между столкновениями молекула пролетает различные отрезки пути.

Расстояние, которое молекула проходит двумя последовательными столкновениями называется длиной свободного пробега.

Обозначим эту величину буквой l . Из вышесказанного следует, что l является случайной величиной и характеризуется функцией распределения.

Вычислим среднее значение длины свободного пробега

Параметр λ в функции распределения f (l) имеет смысл средней длины свободного пробега молекулы.

Очевидно, что значение λ должно зависеть как от размеров молекул, так и от их тела.

Расчет дает

90

λ = 2π1d2n ,

где d - эффективный диаметр молекулы

n- концентрация молекул.

При нормальных условиях в газах

λ≈10−7 .

Промежуток времени между двумя последовательными столкновениями молекулы называется временем свободного пробега.

Эта величина также является случайной и можно определить среднее время свободного пробега τ. Расчет дает

τ = λυ ,

где υ - средняя арифметическая скорость молекул газа.

Частота столкновений (среднее число столкновений) молекулы есть величина равная среднему количеству столкновений молекулы в единицу времени.

Обозначим частоту столкновений z .

Запишем:

z = 2πd2n υ .

Диффузия в газах

Диффузией называется процесс самопроизвольного выравнивания концентрации вещества в системе. Пусть концентрация молекул газа n изменяется вдоль некоторого направления z .

перпендикулярную оси z и выделим участок поверхности, площадь которого обозначим dS .