
02_Молекулярная_физика
.pdf
61
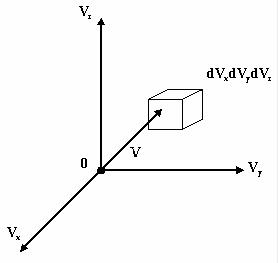
Точка в пространстве скоростей определяет проекции скорости υx ,υy ,υz
некоторой молекулы, а расстояние от этой точки до начала осей есть модуль скорости.
υ =  υ2x + υ2y + υ2z .
υ2x + υ2y + υ2z .
Каждой молекуле в обычном пространстве соответствует одна точка в υ- пространстве. Следовательно, полное число точек NT в υ- пространстве равно числу молекул N в объеме обычного пространства.
NT = N .
Обозначим ρυ - число точек υ- пространства в единичном объеме υ- пространства.
Предположим, что
ρυ(υ)= NTϕ(υ)= Nϕ(υ),
где ϕ(υ)- некоторая неизвестная функция.
Построим в υ- пространстве две сферы радиусами υ и (υ+dυ), dυ << υ. Центры сфер совпадают с началом системы координаты (υx ,υy ,υz ).
Найдем число точек dNT внутри такого слоя толщиной dυ.
dNT = ρυdυm = ρυ4πυ2dυ = NTϕ(υ)4π υ2dυ,
dNT = Ndω(υ)= Nf (υ)dυ ( ).
Запишем
dN = Ndω(υ)= Nf (υ)dυ, ( )
где dN - число молекул, модули скорости которых имеют значения в интервале
(υ,υ+dυ).
Очевидно, что
NT = N , dNT = dN ,
Nϕ(υ)4π υ2dυ = Nf (υ)dυ, f (υ)= ϕ(υ)4π υ2 .
Выделим элементарный объем V- пространства в виде параллелепипеда dVxdVydVz . Число точек в этом элементарном объеме равно
dNT = ρυdVx dVy dVz = Nϕ(V)dVx dVy dVz .
62
Обозначим,
dω(dυxdυydυz ) - вероятность того, что скорость молекул имеет проекции в
интервалах значений (υx ,υx +dυx ), (υy ,υy +dυy ), (υz , υz +dυz ).
dω(υx ), dω(υy ), dω(υz ) - вероятность того, что проекции скорости молекулы имеют значение в интервалах (υx ,υx +dυx ), (υy ,υy +dυy ), (υz , υz +dυz ).
По закону умножения вероятностей
dω(υx , υy , υz )= dω(υx ) dω(υy ) dωz (υz ), dω(υx ,υy , υz )= f (υx ) f (υy ) fz (υz )dυxdυydυz .
Умножим на число молекул N
Ndω(υx , υy , υz )= Nf (υx )f (υy )f (υz )dυxdυydυz ,
dN = Nf (υx )f (υy )f (υz )dυxdυydυz . ( )
С другой стороны
dNT = ρVdVxdVydVz = Nϕ(V)dVxdVydVz . |
( ) |
Из ( ) и ( ) получим |
|
Nϕ(V)dVxdVydVz = Nf (Vx )f (Vy )f (Vz )dVxdVydVz , ϕ(V)= f (Vx )f (Vy )f (Vz ),
f (V)= f (Vx )f (Vy )f (Vz ) 4π V2 .
Итак, получаем для f (V)
63
1
fU (U)= 2kT 2m0
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
m0 |
|
|
1 |
|
|
2kT |
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
||||||||||||||||
|
2 |
|
2 |
|
|
|
||||||||||||||||
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
π |
|
|
|
m0 |
|
U |
|
exp |
|||||||||
|
2π kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
m0 |
|
|
3 |
|
|
|
|
|
m0V |
2 |
|
|
|||
f (V) |
|
|
|
|
|
2 |
2 |
|
|
|
|
|||||||||||
= |
|
|
|
|
|
|
|
|
− |
|
|
|
||||||||||
4π |
|
|
|
|
|
|
|
V |
|
|
|
|
||||||||||
|
|
|
|
|
|
exp |
2k T |
. |
|
|||||||||||||
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
||||||||
m |
2kT |
|
|
|
0 |
|
|
U |
2 |
|
|
|
||
2kT m |
|
, |
||
0 |
|
|
||
Эта формула называется распределением Максвелла. Здесь:
m0 - масса молекулы,
T - температура газа,
f (V) - вероятность того, что модуль скорости имеет значение, находящееся на единичном интервале вблизи значения V .
Свойства распределения Максвелла
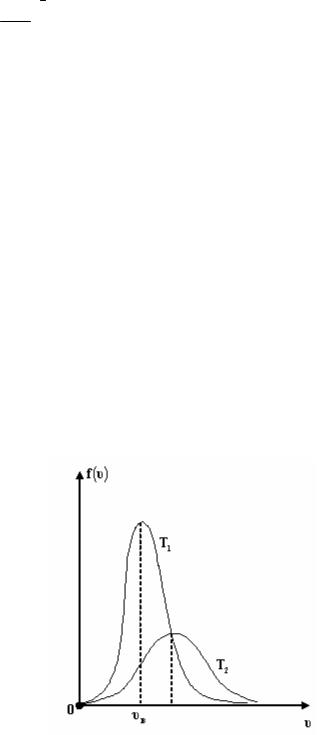
График функции f (V) представлен на рисунке. Функция начинается от 0 при V = 0 , достигает максимума и асимптотически спадает до нуля при V → ∞. График не симметричен. С увеличением температуры T максимум функции уменьшается и график расширяется.
Условие нормировки f (V):
∞∫f (V)dV =1.
0
Значение модуля скорости, при котором f (V) достигает максимума, называется наиболее вероятной скоростью υв .
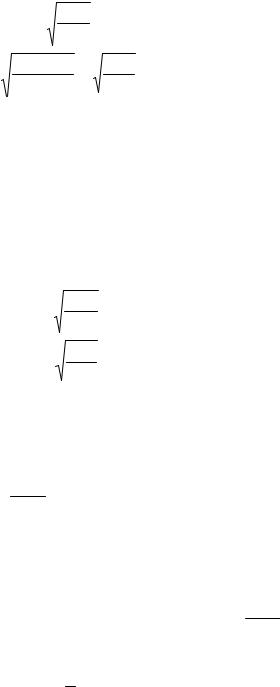
Значение υв находится из условия экстремума: |
|||
|
df (V) |
|
|
|
|
= 0 , |
|
|
dV |
||
|
|
υ=υв |
|
|
|
||
64
|
m |
|
|
3 |
|
|
|
|
|
m |
υ2 |
|
|
|
|
|
|
m |
υ2 |
|
|
m |
υ |
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
в |
= 0 , |
|||||||||||||||
4π |
|
|
|
2υexp |
− |
0 |
в |
|
+ υ2exp |
− |
|
0 |
в |
|
− |
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2πkT |
|
|
|
|
|
|
2k T |
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
2k T |
|
|
|
|||||||||||||
|
|
|
|
|
m0 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
m0υв |
|
|
m0υв |
|
= 0 . |
|
|
|||||||||
|
4π |
|
|
|
|
|
υв exp − |
|
|
2 − |
|
|
|
|
|
|
|||||||||||
|
|
|
|
2k T |
k T |
|
|
|
|||||||||||||||||||
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При υв = 0 и υв → ∞ функция имеет не максимум, а минимум. Следовательно, остается условие
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 − |
|
m0υв |
|
= 0 |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
k T |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
υв |
= |
2k T , |
|
|
|
|
|
|
|
||||||
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
||||
υв = |
2k T NA |
|
= |
|
2RT . |
|
|
|
|
|||||||
|
m0 NA |
|
|
|
|
M |
|
|
|
|
|
|||||
Здесь M - молярная масса газа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Средняя и средняя квадратичная скорость |
||||||||||||||||
Найдем среднюю скорость < υ > |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||
∞ |
|
|
m0 |
|
|
∞ |
|
|
|
|
m0υ |
2 |
|
|||
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
||||||
< υ >= ∫υf (υ)dυ = 4π |
|
|
|
|
|
∫ |
υ |
|
− |
|
|
|||||
2πkT |
|
exp |
2kT |
dV , |
||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
||||||
< υ |
>= |
8kT , |
|
|
|
|
|
|
||||||||
|
|
|
|
πm0 |
|
|
|
|
|
|
|
|
||||
< υ >= |
8RT . |
|
|
|
|
|
|
|||||||||
|
|
|
|
πM |
|
|
|
|
|
|
|
|
||||
Величина < υ > называется также средней арифметической скоростью.
Обозначим:
εn - кинетическая энергия поступательного движения молекулы.
εn = m20υ2 , εn = εn (υ).
Обозначим:
< εn > - средняя кинетическая энергия поступательного движения.
Вычислим < εn >
|
m0υ |
2 |
|
m0 |
|
3 |
|
m0 |
∞ |
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
< εn >= ∫εn (υ)f (υ)dυ = ∫ |
|
|
f (υ)dV = 4π |
|
|
|
|
|
∫ |
υ4exp |
− |
2 |
|
|
|
2 |
|||||||
|
|
|
2π kT |
|
|
0 |
|
|
|||
m0υ2 dυ.
2kT
Расчеты дают значение:
< εn >= 32 kT .
Обозначим: υс - скорость, при которой кинетическая энергия молекулы равна средней кинетической энергии.

65
Найдем значение υс .
|
|
m0υc2 |
|
= |
|
3 |
kT , |
|
|
2 |
2 |
|
|||||
|
|
|
|
|
||||
υc = |
3kT , |
|
υc = |
3RT . |
||||
|
|
m0 |
|
|
|
|
M |
|
Величина υc называется средней квадратичной скоростью.
Распределение Максвелла для относительной скорости
Относительной скоростью молекулы называется величина
U = υ .
υв
Введем два интервала dυ и dU таким образом, что любому значению модуля скорости из интервала (υ, υ + dυ) взаимно однозначно соответствует значение относительной скорости из интервала (U, U + dU). Интервалы dυ и dU называются соответствующими друг другу.
Попадание модуля скорости в интервал (υ, υ+ dυ) и попадание относительной скорости в соответствующий интервал (U, U + dU) этого события, которые имеют одну и ту же вероятность.
dω(υ, υ+ dυ)= dω(U,U + dU).
Запишем вероятности через функции распределения fυ(υ)dυ = fU (U)dU ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|
|
|
dυ |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
dU = d |
υв |
= |
υв |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
fυ(υ)dυ = fU |
(U) |
dυ |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υв |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
fU (U)= υв fυ(υ), |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
fU (U)= υв fυ(υвU), |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
m0υ |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
fU (U)= υв 4π |
|
|
|
|
|
|
|
υ |
|
|
|
|
|
− |
|
|
|
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
exp |
|
2kT |
|
|
|
|
|
|||||||||||||||||||||
Подставим: |
|
|
|
|
|
|
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ = υв U = |
|
2kT U , |
|
|
υв = |
|
|
2kT , |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2kT |
|
2 |
|
|
m |
|
|
|
|
1 |
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
m |
2kT |
|
|
|||||||||
|
0 |
|
2 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
fU (U)= |
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U2 |
exp |
− |
0 |
|
U2 |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
m0 |
|
2πkT |
|
π |
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
2kT m0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
U2 exp(− U2 ), |
|
|
|
|
|
|
|
|||||||||||||||||
опустим индекс |
|
|
fU (U)= 4π 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 U2 exp(− U2 ). |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
fU (U)= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

66
Это распределение Максвелла для относительной скорости. Функция f (U) не содержит массы, температуры и поэтому она гораздо удобнее в расчетах.
Распределение молекул идеального газа по модулю скорости
Пусть идеальный газ находится в равновесном состоянии и n - концентрация молекул. Поставим следующую задачу: определить число молекул в единице объема газа, величина скорости, которых имеет значения в
интервале (υ1,υ2 ).
Перейдем к относительным скоростям:
U1 |
= |
υ1 |
, |
U2 |
= |
υ2 |
. |
|
|||||||
υв |
|
||||||
|
|
|
|
|
υв |
||
Очевидно, что интервалы |
(υ1,υ2 ) |
и |
(U1,U2 ) будут соответствующими, и |
||||
будем искать сначала число молекул, относительные скорости которых имеют значения в интервале (U1,U2 ).
Обозначим dN - число молекул, относительные скорости которых лежат в интервале (U,U +dU).
Очевидно:
dN = Ndω(U,U +dU)= Nf (U)dU .
Интегрируя, получаем искомую величину ∆N
U |
Nf (U)dU = |
4N |
U |
|
∆N = ∫2 |
∫2U2exp(−U2 )dU , |
|||
U1 |
|
|
π |
U1 |
|
4 |
U |
|
|
∆N = |
N ∫2U2exp(−U2 )dU . ( ) |
|||
|
π |
U1 |
|
|
Для того чтобы найти число частиц в единице объема, скорости которых лежат в заданном интервале, разделим обе части ( ) на объем, занимаемый газом V . Обозначим:
|
∆n = |
∆N |
, |
n = |
N |
, |
|
|
V |
V |
|||||
|
|
|
|
|
|
||
|
4 |
|
U |
|
|
|
|
∆n = |
n ∫2U2exp(−U2 )dU . |
||||||
|
π |
|
U1 |
|
|
|
|
Распределение молекул по кинетической энергии
Запишем
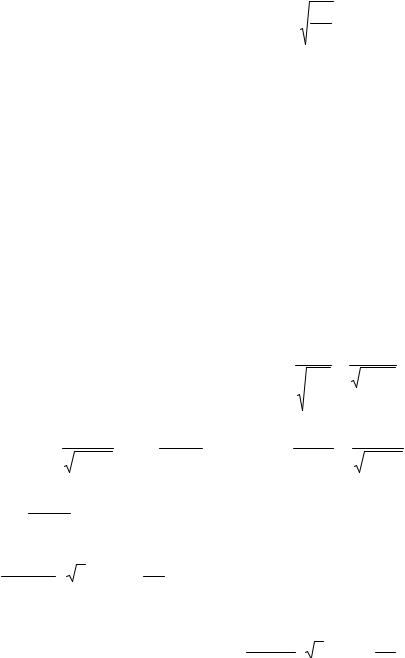
|
67 |
|
|
ε = |
m0υ2 |
, |
|
|
|||
|
2 |
|
|
υ = |
|
2ε , |
|
|
|
m0 |
|
где ε- кинетическая энергия поступательного движения молекулы. Введем два бесконечно малых интервала dυ и dε, которые соответствуют
друг другу. Это означает, что любому значению скорости из интервала (υ,υ+dυ) взаимно однозначно соответствует значение кинетической энергии из интервала (ε,ε + dε). Обозначим вероятность попадания скорости в интервал dω(υ,υ+dυ), а вероятность попадания кинетической энергии в соответствующий интервал dω(ε,ε+dε).
Очевидно, что эти вероятности одинаковы dω(υ,υ+dυ)= dω(ε,ε+dε),
f (υ)dυ = f (ε)dε,
где f (ε) - функция распределения кинетической энергии.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (ε)= f (υ) |
dυ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dυ |
|
|
1 |
|
|
2 |
|
|
|
|
1 |
|
|
|
dε |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m0ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dε |
2 |
|
|
m0 |
|
2ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
m |
|
|
3 |
|
|
|
|
|
|
|
|
m |
|
|
υ |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
f (ε)= f (υ) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
= 4π |
|
|
0 |
|
|
|
υ2 exp − |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2m0ε |
|
|
|
2π kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m0ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
m0 |
3 |
|
2ε |
|
|
|
|
|
|
m0 |
|
|
|
|
2ε |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
m |
3 |
|
|
|
|
2ε |
|
|
ε |
|
1 |
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
= 4π |
|
3 |
|
|
|
|
|
|
|
|
|
exp |
− |
|
|
1 1 1 = |
||||||||||||||||||||
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
2π kT |
|
m0 |
|
|
|
|
|
2kT |
|
|
m0 |
(2m0ε) |
2 |
|
|
2 |
2 |
|
(π kT) |
|
|
|
m0 |
|
|
kT |
|
2 |
2 |
m |
02 |
ε |
2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
= |
2π |
ε |
|
|
|
− |
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
exp |
kT |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(π kT) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(ε)= |
|
|
|
2π |
ε |
|
|
|
|
− |
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
exp |
kT |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(π kT) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Пусть N - число молекул газа. |
|
|
Обозначим ∆N - число молекул, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кинетическая энергия которых имеет значение из интервала (ε1,ε2 ). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Запишем:
dN = Ndω(ε), dω(ε)= f (ε)dε, dN = Nf (ε)dε,
ε2
∆N = N ∫f (ε)dε.
ε1

68
Распределение Больцмана
Выделим элементарный объем пространства dxdydz . Обозначим dω(x, y,z) - вероятность того, что частицы находятся в элементарном объеме dxdydz , выбранном в окрестности точки с координатами (x, y,z).
Очевидно, что dω(x,y,z) зависит от величины dxdydz и некоторой функции от координат f (x, y,z).
dω(x, y,z)= f (x, y,z)dxdydz . ( )
Очевидно, что f (x, y,z) имеет смысл функции распределения и для нее справедливо условие нормировки
∫f (x, y,z)dxdydz =1.
V
Будем искать функцию f (x, y,z). Умножим ( ) на число частиц N .
N dω(x, y,z)= N f (x, y,z)dxdydz .
Обозначим
N dω(x, y,z)= dN , dxdydz = dV ,
dN = N f (x, y,z)dV .
где dN - число частиц в объеме dV .
dNdV = N f (x, y,z),
м13 , n = N f (x, y,z),
где n - число частиц в единице объема или концентрация частиц. Очевидно, что тогда
f (x, y,z)= Nn .
Рассмотрим идеальный газ, молекулы которого находятся в однородном поле тяжести Земли, т.е. в поле консервативных сил.

69
Выделим столб газа с поперечным сечением площадью dS = dx dy .
В столбе выделим слой газа толщиной dz и площадью оснований dS . Этот слой находится в равновесии. Рассмотрим силы, действующие на слой.
На верхнее и нижнее основание действуют силы давления, сумма
которых равна
Frg = p dS k +(p +dp)dS(−k)= −dp dS k ,
где dp - приращение давления газа при удалении от нижнего основания к верхнему, k - орт оси z .
На каждую молекулу газа действует сила тяжести, которую обозначим F1 .
Обозначим n - концентрация молекул газа. Тогда на все молекулы слоя действует сила тяжести
Fm = F1 ndS dz .
Запишем для слоя второй закон Ньютона:
Fg + Fm = 0 ,
−dpdSk + F1ndSdz = 0 k ,

|
70 |
|
|
|
|
−dpk k + F1 kndz = 0 , |
|||||
r |
r |
|
r |
cosα = F1z |
, |
F1 |
k = F1 |
|
k |
||
−dp + F1z ndz = 0 .
Обозначим υ- потенциальная молекула газа в поле тяжести.
Тогда
F1z = − ddzυ ,
−dp − ddzυ ndz = 0 , dp = −ndυ.
Уравнение состояния для идеального газа p = nkT .
Возьмем дифференциал, предполагая, что выполняется условие
T = const , dp = kTdn ,
kTdn = -ndυ, dnn = −kTdυ .
Интегрируем: при T = const , изотермическая атмосфера
∫ |
dn |
|
= − |
1 |
|
|
∫dυ, |
||||||||||
|
kT |
||||||||||||||||
|
n |
|
|
|
|
|
|
|
|||||||||
ln n = − |
|
|
υ |
|
+ const . |
||||||||||||
kT |
|||||||||||||||||
Определим следующие условия |
|
|
|
|
|
|
|
||||||||||
|
|
|
n = n0 . |
||||||||||||||
υ = 0, |
|
|
|
||||||||||||||
Тогда |
|
= const , |
|||||||||||||||
|
ln n0 |
|
|||||||||||||||
ln n = - |
|
|
υ |
|
+ln n0 , |
||||||||||||
|
kT |
||||||||||||||||
|
|
|
n |
|
|
|
|
υ |
|
|
|||||||
|
ln |
|
|
= - |
|
|
, |
||||||||||
|
n0 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
kT |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
υ |
|||||
n = n0exp |
− |
|
|
|
. |
||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|||||
Вобщем случае υ- есть функция координат x, y,z .
υ= υ(x, y,z),
n= n0exp - υ(x, y,z) .
kT
Это распределение Больцмана.
Здесь
n0 - концентрация частиц в точках, где υ = 0 .
n - концентрация частиц в точке, где потенциальная энергия частицы равна υ. T - температура системы.
